【位运算】【前缀和】个人练习-Leetcode-1177. Can Make Palindrome from Substring
题目链接:https://leetcode.cn/problems/can-make-palindrome-from-substring/description/
题目大意:给出一个字符串s,每次query给出l, r, k,要求判断子串s[l:r+1]在经过k次操作后是否能变为回文串。一次操作可以将子串内的一个字符变为任意一个其他字符。并且子串顺序可以任意改变。
思路:因为有很多query,自然想到会有重复计算,要检查超时,那么就想到前缀和。用pre[j][i]记录到i为止字母j出现的次数。那么子串内字母j出现的次数即为pre[j][r+1-l]。
对于子串,如果长度为奇数,那么回文与否与中间的字符无关,我们可以忽略。因此处理的总是一个总长度为偶数的子串。统计子串中每个字母的出现次数,可以知道,【奇数出现的次数】必然是偶数,因为只有偶数个奇数+若干偶数才能使得和(子串总长度)为偶数。
那么对于cnt个出现奇数次的字母,我们进行k次操作可以最多让2*k长度的子串变为回文。而对于出现偶数次的字母,只需将其对称排列即可。因此判断条件变为cnt / 2 <= k
完整代码
class Solution {
public:vector<bool> canMakePaliQueries(string s, vector<vector<int>>& queries) {int N = s.length();int pre[26][10001] = {};for (int i = 0; i < N; i++) {int idx = s[i]-'a';pre[idx][i+1] = pre[idx][i]+1;for (int j = 0; j < 26; j++) {if (j != idx && i > 0)pre[j][i+1] = pre[j][i];}}vector<bool> res;for (auto q: queries) {int l = q[0], r = q[1], k = q[2];char mid = s[(l+r)/2];bool flag = (r+1-l)%2;int arr[26] = {};if (flag)arr[mid-'a']--;int cnt = 0;for (int j = 0; j < 26; j++) {arr[j] += pre[j][r+1] - pre[j][l];if (arr[j] & 1 == 1) {cnt++;}}if (cnt / 2 <= k) {res.emplace_back(true);}else {res.emplace_back(false);}}return res;}
};
然而,碰到大的测试样例的时候会超时…那么就不得不求助高效的位运算了。
我们用一个二进制数组存储前缀和,每个二进制数一共26位,代表某个字母在i位置前的奇偶性。奇偶性运算用异或操作^来实现。
int N = s.length();vector<int> pre(N+1, 0);for (int i = 0; i < N; i++) {pre[i+1] = pre[i] ^ (1 << s[i]-'a'); }
如何统计子串中的字母的奇数的个数呢?这就是数一下【代表该区间的二进制数】(通过前缀和做差得到)中1的个数。
int l = q[0], r = q[1], k = q[2];int cnt = 0;int x = pre[r+1] ^ pre[l];while (x > 0) {x &= x - 1;cnt++;}
x &= x-1操作将 x 的二进制表示中最低位的 1 翻转成 0,并将所有更低位的位都清零。这是一个位运算技巧,快速计算二进制数中1的个数。
另外,由于乘法比除法更加快速,我们就不考虑是否忽略子串最中间的字母了,即使它使得x中1的个数增加了,也只不过增加1而已,我们将能够处理的上限改为2*k+1即可。
if (cnt <= 2*k+1)res.emplace_back(true);elseres.emplace_back(false);
完整代码
class Solution {
public:vector<bool> canMakePaliQueries(string s, vector<vector<int>>& queries) {int N = s.length();vector<int> pre(N+1, 0);for (int i = 0; i < N; i++) {pre[i+1] = pre[i] ^ (1 << s[i]-'a'); }vector<bool> res;for (auto q: queries) {int l = q[0], r = q[1], k = q[2];int cnt = 0;int x = pre[r+1] ^ pre[l];while (x > 0) {x &= x - 1;cnt++;}if (cnt <= 2*k+1)res.emplace_back(true);elseres.emplace_back(false);}return res;}
};
相关文章:

【位运算】【前缀和】个人练习-Leetcode-1177. Can Make Palindrome from Substring
题目链接:https://leetcode.cn/problems/can-make-palindrome-from-substring/description/ 题目大意:给出一个字符串s,每次query给出l, r, k,要求判断子串s[l:r1]在经过k次操作后是否能变为回文串。一次操作可以将子串内的一个字…...
最小相位系统
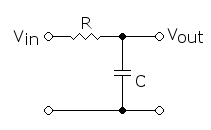
最小相位系统 1、传递函数 一个线性系统的响应。 比如一个RC低通滤波器: 交流分量在电容的充放电中被滤除掉,通过设置电容器的电容值,以及电阻值,能够控制这种滤除能力,这个参数为RC。 电容的电抗为 1 / j w C 1/j…...

css系列:进度条
前言 技术来源于需求,近期遇到了做语音的需求,有个调整语速和音量的进度条,UI组件库的进度条大部分不支持拖动和点击修改当前进度,所以自己手写了一个。 实现思路 MDN文档介绍 <input type"range"> - HTML&am…...

QT中为程序加入超级管理员权限
QT中为程序加入超级管理员权限 Chapter1 QT中为程序加入超级管理员权限1. mingw编译器2. MSVC编译器3. CMAKE Chapter2 如何给QT程序添加管理员权限(UAC)的几种方法1、Qt Creator中方案一:(仅适用于使用msvc编译器)方案二:&#x…...
)
共识算法之争(PBFT,Raft,PoW,PoS,DPoS)
文章目录 共识算法拜占庭容错技术(Byzantine Fault Tolerance,BFT)PBFT:Practical Byzantine Fault Tolerance,实用拜占庭容错算法Raft协议POW(Proof of Work)工作量证明机制POSDPoS(Delegated Proof of St…...

抽象的java入门1.3.0
前言: 在1.2.0版本中我们介绍了public class hello {}并从中提取出两个新概 修饰符和作用域 public class hello {public static void main(String[] args) {System.out.println("Hello World");} } 正片: 这一期把剩余的内容刨析出来 pub…...

【Oracle生产运维】表空间可用性告警排查处理
1 前言 在生产环境中,一般设置表空间告警阈值是90%,在接到监控报警后,并不是需要立刻对表空间进行扩容。 决定是否扩容主要看表空间最近的增量是多少,假如剩余10%的空间还能支持1个月的增量,那就不需要急着扩容。如果…...

mac Network: use --host to expose
本地启动无法访问,这个不是权限问题是mac 主机端口安全策略,现在我们只需要开启端口自动检测就可以 npm run dev --host 网络:未暴露 方案一 1、执行 npm run dev -- --host 方案二 1、请在 vite.config.js server: {host: true } 1…...

ChatGPT-4o体验demo
OpenAI 最近推出了其最新的人工智能语言模型——GPT-4O。该模型是在原有 GPT-4 的基础上进行优化而成,旨在提升生成质量和响应速度。GPT-4O 采用了更加高效的架构设计,使其在处理复杂文本时表现出更快的速度和更高的准确性。GPT-4O 在训练过程中融入了最…...
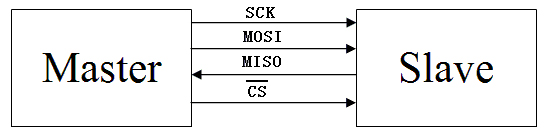
FPGA SPI采集ADC7606数据
一,SPI总线的构成及信号类型 SPI总线只需四条线(如图1所示)就可以完成MCU与各种外围器件的通讯: 1)MOSI – Master数据输出,Slave数据输入 2)MISO – Master数据输入,Slave数据输出 3)SCK – 时钟信号,由Master产生 4)/CS – Slave使能信号,由Master控制。 在一个SPI时…...
html three.js 引入.stl模型示例
1.新建一个模块用于放置模型 <div id"chart_map" style"width:800px;height:500px"></div> 2. 引入代码根据需求更改 <!-- 在head或body标签内加入以下链接 --> <script src"https://cdn.jsdelivr.net/npm/three0.137/build/t…...

从零手写实现 nginx-11-文件处理逻辑与 range 范围查询合并
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

Java算法-力扣leetcode-167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 ****非递减顺序排列 ** ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < index2 < n…...

实战 | YOLOv10 自定义数据集训练实现车牌检测 (数据集+训练+预测 保姆级教程)
导读 本文主要介绍如何使用YOLOv10在自定义数据集训练实现车牌检测 (数据集训练预测 保姆级教程)。 YOLOv10简介 YOLOv10是清华大学研究人员在Ultralytics Python包的基础上,引入了一种新的实时目标检测方法,解决了YOLO以前版本在后处理和模型架构方面…...

自定义类型:结构体+结构体内存对齐+结构体实现位段
结构体内存对齐实现位段 一.结构体1.结构体的声明2.结构体变量成员访问操作符3.结构体传参4.匿名结构体5.结构的自引用 二.结构体内存对齐1.对齐规则2.为什么存在内存对齐?3.修改默认对齐数 三.结构体实现位段1.什么是位段2.位段的内存分配3.位段的跨平台问题4.位段…...
 command)
0109__strip(1) command
strip(1) command_linux strip-CSDN博客...

英码科技推出鸿蒙边缘计算盒子:提升国产化水平,增强AI应用效能,保障数据安全
当前,随着国产化替代趋势的加强,鸿蒙系统Harmony OS也日趋成熟和完善,各行各业都在积极拥抱鸿蒙;那么,边缘计算要加快实现全面国产化,基于鸿蒙系统开发AI应用势在必行。 关于鸿蒙系统及其优势 鸿蒙系统是华…...

从军事角度理解“战略与战术”
战略与战术,均源于军事术语。 战略(Strategy),源自希腊语词汇“strategos(将军)”和“strategia(军事指挥部,即将军的办公室和技能)”。指的是指挥全局性作战规划的谋略…...

最短路径——迪杰斯特拉与弗洛伊德算法
一.迪杰斯特拉算法 首先对于最短路径来说:从vi-vj的最短路径,不用非要经过所有的顶点,只需要找到路径最短的路径即可; 那么迪杰斯特拉的算法:其实也就与最小生成树的思想类似,找到较小的,然后…...
6.7.11 一种新的迁移学习方法可提高乳房 X 线摄影筛查中乳腺癌的诊断率
分割是一种将图像分割成离散区域的技术,以便将感兴趣的对象与周围环境分开。为了制定治疗计划,分割可以帮助医生测量乳房中的组织量。 二元分类问题的目的是将输入数据分为两组互斥的数据。在这种情况下,训练数据根据要解决的问题以二进制格…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
