OpenCV学习(4.8) 图像金字塔
1.目的
在这一章当中,
- 我们将了解图像金字塔。
- 我们将使用图像金字塔创建一个新的水果,“Orapple”
- 我们将看到这些功能: cv.pyrUp() , cv.pyrDown()
在通常情况下我们使用大小恒定的图像。但在某些情况下,我们需要使用不同分辨率的同幅图像。例如,在搜索图像中的某些内容如脸部信息时,并不确定该内容在图像中占据的大小。在这种情况下,我们需要创建一组不同分辨率的相同图像,并在所有图像中搜索该内容。这些不同分辨率的图像被称为图像金字塔(因为当它们堆叠排列时,底部为最高分辨率图像而顶部为最低分辨率图像,看起来像金字塔)。
图像金字塔有两种: 1)高斯金字塔和 2)拉普拉斯金字塔
通过去除较低级别图像(较高分辨率)中的连续行和列来形成高斯金字塔中的较高级别图像(较低分辨率)。较高级别图像的每个像素值由低一级别图像的 5 个像素值高斯加权得到,由此图像面积减少到原来的四分之一。这些图像被称为 Octave(组)。当我们在金字塔中上升时(即分辨率降低),重复相似的操作。同理,在金字塔中下降时,每个级别的图像面积大小为上一级的四倍。我们可以使用 cv.pyrDown() 和 cv.pyrUp() 函数获取高斯金字塔。
2. 图像金字塔
import cv2
import numpy as np
from matplotlib import pyplot as plt# 读取原始图像
image = cv2.imread(r'D:\study\EmotionDetection_RealTime-master\data\data\te\13.jpg', cv2.IMREAD_COLOR)# 创建图像金字塔
# 这里我们将创建三个层次的金字塔
pyramid_images = [image]
cv2.imshow('image',image)
downscaled_image = cv2.pyrDown(image)
cv2.imshow('downscaled_image',downscaled_image)upsampled_image = cv2.pyrUp(image)cv2.imshow('upsampled_image',upsampled_image)# 等待按键后关闭所有窗口
cv2.waitKey(0)
cv2.destroyAllWindows()2.1 cv2.pyrDown()
cv2.pyrDown()函数用于对图像进行下采样,即减少图像的分辨率。它通常用于创建图像金字塔的较低层次。下采样的具体过程是:
- 对图像进行高斯模糊。
- 将模糊后的图像沿水平方向和垂直方向各减半。
这样,原始图像的分辨率被降低了一半。

2.2 cv2.pyrUp()
cv2.pyrUp()函数用于对图像进行上采样,即增加图像的分辨率。它通常用于创建图像金字塔的较高层次。上采样的具体过程是:
- 将图像复制到一个新的尺寸更大的图像中。
- 在新图像的边缘填充零。
- 对新图像进行高斯模糊。
这样,原始图像的分辨率被提高了一倍。

原始图像的分辨率通常指的是图像在水平和垂直方向上的像素数量。这是图像的一个重要属性,因为它决定了图像的清晰度和细节水平。
例如,一个分辨率为1024x768的图像意味着图像在水平方向上有1024个像素,在垂直方向上有768个像素。这意味着图像的总面积是786432个像素(1024x768)。
分辨率通常以像素为单位表示,但也可以用其他单位,如英寸(inches)或厘米(centimeters)。在这种情况下,分辨率指的是每英寸或每厘米的像素数量。例如,一个分辨率为300dpi(dots per inch)的图像意味着每英寸有300个像素。
相关文章:

OpenCV学习(4.8) 图像金字塔
1.目的 在这一章当中, 我们将了解图像金字塔。我们将使用图像金字塔创建一个新的水果,“Orapple”我们将看到这些功能: cv.pyrUp() , cv.pyrDown() 在通常情况下我们使用大小恒定…...

【TB作品】msp430f5529单片机,dht22,温湿度传感器,OLED显示屏
使用DHT22温湿度传感器和OLED显示屏的单片机项目 博客名称 利用MSP430单片机读取DHT22并显示温湿度 作品功能 本项目利用MSP430单片机读取DHT22温湿度传感器的数据,并将温湿度信息显示在OLED显示屏上。通过这个项目,您可以学习如何使用单片机与传感器…...

Kotlin 异常处理
文章目录 什么是异常抛出异常通过异常信息解决异常捕获异常 什么是异常 我们在运行程序时,如果代码出现了语法问题或逻辑问题,会导致程序编译失败或退出,称为异常。运行结果会给出一个一长串的红色字,通常会给出异常信息…...

nltk下载报错
捣鼓voice_clone时报错: 报错信息: mport nltk nltk.download(‘cmudict’)For more information see: https://www.nltk.org/data.htmlAttempted to load tokenizers/punkt/PY3/english.pickleSearched in: - ‘/home/zhangshuai/nltk_data’ - ‘/hom…...

Vulnhub-DC5
靶机IP:192.168.20.139 kaliIP:192.168.20.128 网络有问题的可以看下搭建Vulnhub靶机网络问题(获取不到IP) 信息收集 nmap扫下端口及版本 dirsearch扫下目录 LinuxphpNginx 环境 我们再去看前端界面,发现在contact界面有能提交的地方,但是经过测试不…...

pytorch 笔记:pytorch 优化内容(更新中)
1 Tensor创建类 1.1 直接创建Tensor,而不是从Python或Numpy中转换 不要使用原生Python或NumPy创建数据,然后将其转换为torch.Tensor直接用torch.Tensor创建或者直接:torch.empty(), torch.zeros(), torch.full(), torch.ones(), torch.…...

vue 创建一个新项目 以及 手动配置选项
【Vue】3.0 项目创建 自定义配置_vue3.0-CSDN博客...

c#快速获取超大文件夹文件名
c#快速获取超大文件夹文件名 枚举集合速度快:(10万个文件) //by txwtech IEnumerable<string> files2 Directory.EnumerateFiles("d:\aa", "*.xml", SearchOption.TopDirectoryOnly);//过滤指定查询xml文件 慢: var fi…...

华为OD技术面试-最小异或-2024手撕代码真题
题目:最小异或 给你两个正整数 num1 和 num2 ,找出满足下述条件的正整数 x : x 的置位数和 num2 相同,且 x XOR num1 的值 最小 注意 XOR 是按位异或运算。 返回整数 x 。题目保证,对于生成的测试用例, x 是 唯一确定 的。 整数的 置位数 是其二进制表示中 1 的数目。 示…...

基于SpringBoot+Vue单位考勤系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝1W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟 感兴趣的可以先收藏起来,还…...

Anaconda软件:安装、管理python相关包
Anaconda的作用 一个python环境中需要有一个解释器, 和一个包集合. 解释器: 根据python的版本大概分为2和3. python2和3之间无法互相兼容, 也就是说用python2语法写出来的脚本不一定能在python3的解释器中运行. 包集合:包含了自带的包和第三方包, 第三…...

pinia 重置状态插件
一、前言 测试提出,登出登录后,再次进入页面后。页面的查询项非初始状态。检查后发现,是因为查询项的值存到了store呢,从store中获取,故需要一个重置store的方法 二、pinia 查阅pinia官网后,发现pinia提…...
)
一千题,No.0049(跟奥巴马一起编程)
美国总统奥巴马不仅呼吁所有人都学习编程,甚至以身作则编写代码,成为美国历史上首位编写计算机代码的总统。2014 年底,为庆祝“计算机科学教育周”正式启动,奥巴马编写了很简单的计算机代码:在屏幕上画一个正方形。现在…...

《python程序语言设计》2018版第5章第46题均值和标准方差-上部(我又一次被作者的出题击倒)
第N次被作者打倒了,第5章46题解题上集的记录 计算均值的代码段 step_num 0num_c 0 pow_c 0 while step_num < 10:a eval(input("Enter number is: "))num_c apow_c pow(a, 2)step_num 1 t2 num_c / 10这个结果和书里的答案差一点。书里写的是…...

自己做的精灵图制作,图片合成,卓宠,窗口置顶,磁力链下载等工具软件
欢迎使用和提bug,才v1.0.2,有新奇的自己需要的功能可以提给我,我看看能不能做。 网站地址 github...

C++协程
什么是协程 协程(Coroutine)是程序组件,可以在执行过程中暂停并在稍后继续执行。与传统的子例程(如函数或过程)不同,子例程一旦调用,必须等其返回后才能继续执行调用它的代码。协程则可以在执行…...
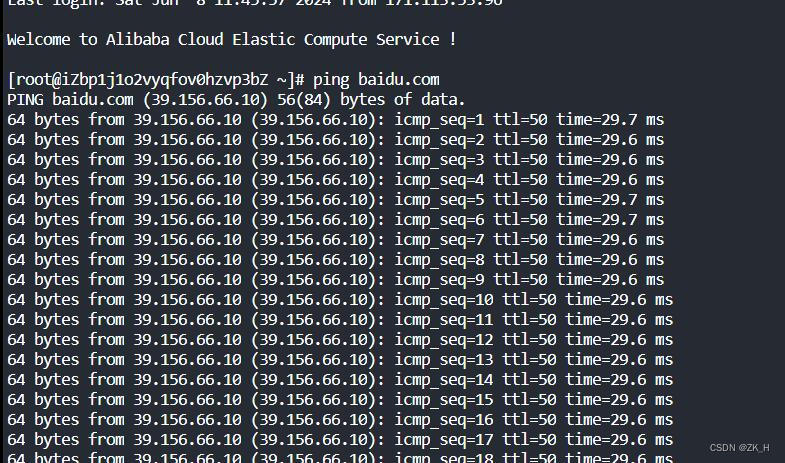
linux系统——ping命令
ping命令可以用来判断对远端ip的连通性,可以加域名也可以加公共ip地址 这里发送出56字节,返回64字节...
防重指令)
vue3第三十七节(自定义插件之自定义指令)防重指令
引言:自定义指令,我们可以通过插件的形式进行全局注册: 例如:在提交按钮请求接口时候,为了防止重复提交,而导致的请求资源浪费,或者是新增提交时候,防止新增相同的数据。 我们的全局…...

面试高频问题----5
一、线程池参数的执行顺序 1.如果线程池中的线程数量小于核心线程数,则创建新的线程来处理任务 2.如果线程池中的线程数量等于核心线程数,但工作队列未满,将任务放入工作队列中执行 3.如果工作队列已满,但线程数小于最大线程数…...
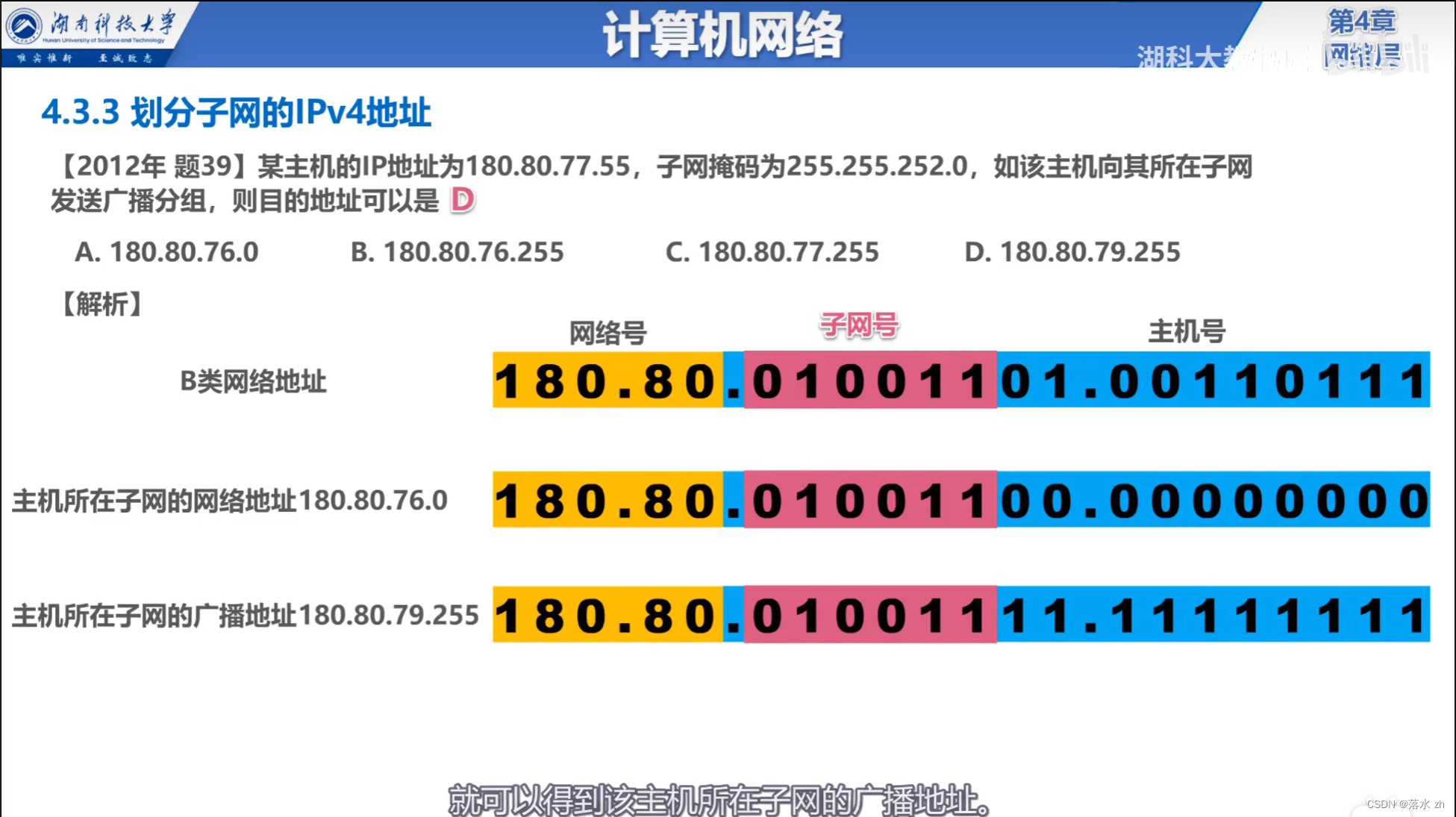
计算机网络 —— 网络层(子网掩码和子网划分)
计算机网络 —— 网络层(子网掩码和子网划分) 网络地址转换NAT子网掩码和子网划分举个例子第一步:看类型第二步:从主机号开始比对第三步:去头去尾 我们今天来看子网掩码和子网划分: 网络地址转换NAT 网络…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
