【Python】selenium使用find_element时解决【StaleElementReferenceException】问题的方法
StaleElementReferenceException 是 Selenium WebDriver 中的一种异常,通常在元素与当前页面的状态不同步时抛出,比如页面已经刷新或导航到另一个页面,但是尝试操作的元素引用仍然是旧页面上的元素。
以下是一些解决 StaleElementReferenceException 的方法:
1. 使用显式等待 wait.until 直到元素可用:
StaleElementReferenceException 的问题是我们获取的元素过时了,无法获取到。如果使用显式等待的方法,可以定期检查元素的状态,直到满足某个条件。
pythonfrom selenium.webdriver.common.by import Byfrom selenium.webdriver.support.ui import WebDriverWaitfrom selenium.webdriver.support import expected_conditions as ECtry:wait = WebDriverWait(driver, 10)xpath=''#xpath路径element= wait.until(EC.presence_of_element_located((By.XPATH, xpath)))driver.execute_script("arguments[0].click();", element) #使用js点击#等于element.click(),只是比click更稳定点)except TimeoutException:print("元素已过时")
记住,处理 StaleElementReferenceException 的最佳实践,通常是使用 Selenium 的显式等待机制,它会自动等待直到元素可交互,从而避免元素过时的问题。
补充until_not的方法:
显性等待是一直等待某个元素的出现,假设我们想要等待直到一个元素不再可见(例如一些弹窗之类的功能过一段时间会消失),可以使用 until_not 这样写:
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as ECtry:# 等待直到元素不再可见,最多等待10秒WebDriverWait(driver, 10).until_not(EC.visibility_of_element_located((By.ID, "myElement")))
except TimeoutException:print("元素在指定时间内仍然可见")
until_not的适用场景:
until_not 是处理需要等待某些条件消失的场景的一个强大工具
在这个例子中,visibility_of_element_located 是一个预期条件函数,它检查指定的元素是否可见。until_not 方法将等待直到这个条件返回 False,即元素不再可见。
注意事项
1. 使用 until_not 时,确保传入的函数是正确的,并且它最终会返回 False,否则会无限期地等待下去。
2. until_not 通常与 expected_conditions 模块中的条件一起使用,但也可以将任何返回布尔值的函数传递给它。
3. 显式等待提供了一种更可靠的方式来处理动态网页内容,特别是当元素的出现或消失是异步操作时。
2. try except 和 is_stale()的使用
如果以上方法不成,可以使用常规的try except捕获错误的方法,直接快捷处理这类问题。
我们遇到StaleElementReferenceException问题的时候,可能会有登录元素有更新,可以使用读取的等待的方式,直到元素不再过时。我们在代码中捕获这个错误,并根据需要进行错误处理,比如重试操作、记录错误信息或者终止测试。
此外,如果我们想要检查一个元素是否过时,可以这样做:
1. 尝试执行一个操作,比如点击,如果元素过时,将会抛出 StaleElementReferenceException。
2. 捕获这个异常,并使用 is_stale() 方法来检查元素是否过时。
from selenium.webdriver.support.ui import WebDriverWaitfrom selenium.webdriver.support import expected_conditions as ECfrom selenium.common.exceptions import StaleElementReferenceException try:element = driver.find_element(By.XPATH, xpath)#.click() # 或者其他操作except StaleElementReferenceException as e:if e.is_stale():print("元素引用已过时")# 可以在这里添加重新获取元素的逻辑else:print("发生其他类型的 StaleElementReferenceException")except Exception as e:print("发生异常:", e))
在这个示例中,如果 element.click() 由于元素过时而抛出 StaleElementReferenceException,我们可以通过 e.is_stale() 来检查是否是因为元素过时导致的异常。
除了上面的方法,一些其他exception也通用的方法,比较推荐:
3. 更新页面:
如果页面已经更新,可能需要重新加载页面driver.refresh()或重新导航到页面以获取最新的元素引用。
4. 检查网络延迟:
如果网络延迟导致页面加载缓慢,可能会引起元素过时。确保网络连接稳定。
5. 减少页面操作:
减少在页面上执行的不必要操作,以减少页面刷新或重新加载的可能性。
通过这些方法,可以有效地处理 StaleElementReferenceException 异常,并确保你的自动化测试脚本能够稳定运行。
相关文章:

【Python】selenium使用find_element时解决【StaleElementReferenceException】问题的方法
StaleElementReferenceException 是 Selenium WebDriver 中的一种异常,通常在元素与当前页面的状态不同步时抛出,比如页面已经刷新或导航到另一个页面,但是尝试操作的元素引用仍然是旧页面上的元素。 以下是一些解决 StaleElementReferenceE…...

Apache IoTDB 分布式架构三部曲(三)副本与共识算法
IoTDB 首创并应用的共识协议统一框架,为用户提供了灵活选择不同共识算法的可能性。 对于一个分布式集群而言,为了使得海量数据场景下集群能够横向扩展,集群需要按照一定的规则将全部数据分成多个子集存储在不同的节点上,从而能够更…...

数据挖掘--聚类分析:基本概念和方法
数据挖掘--引论 数据挖掘--认识数据 数据挖掘--数据预处理 数据挖掘--数据仓库与联机分析处理 数据挖掘--挖掘频繁模式、关联和相关性:基本概念和方法 数据挖掘--分类 数据挖掘--聚类分析:基本概念和方法 聚类分析 聚类分析是把一个数据对象&…...
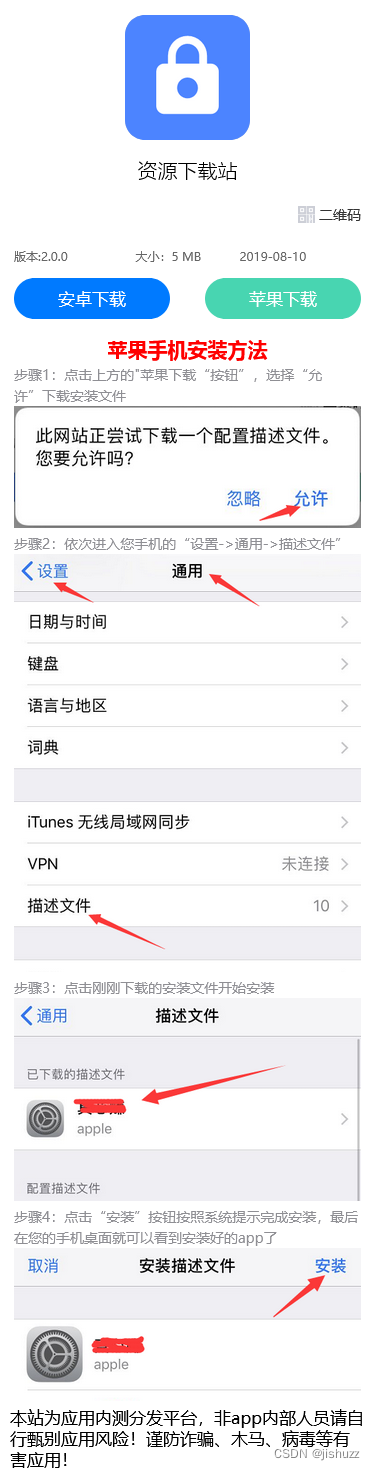
APP单页分发源码下载安卓苹果自动识别apk描述文件免签自动安装
下载地址:APP单页分发源码下载安卓苹果自动识别apk描述文件免签自动安装...

golang定时器使用示例
1.定时器创建与停止 //定时器使用t1 : time.NewTimer(2 * time.Second)<-t1.Cfmt.Println("timer1 fired")t2 : time.NewTimer(5 * time.Second)go func() {fmt.Println("go协程处理中,等待5秒后输出...")<-t2.Cfmt.Println("timer2 fired&quo…...

[FSCTF 2023]Tea_apk
得到密文和密钥 import base64 from ctypes import c_uint32import libnumDELTA 0x9E3779B9def decrypt(v, n, k):rounds 6 int(52 / n)sum c_uint32(rounds * DELTA)y v[0].valuewhile rounds > 0:e (sum.value >> 2) & 3p n - 1while p > 0:z v[p …...
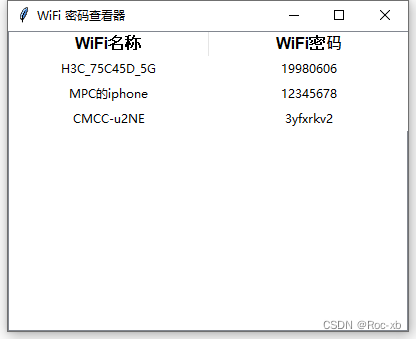
分享一个用python写的本地WIFI密码查看器
本章教程,主要分享一个本地wifi密码查看器,用python实现的,感兴趣的可以试一试。 具体代码 import subprocess # 导入 subprocess 模块,用于执行系统命令 import tkinter as tk # 导入 tkinter 模块,用于创建图形用…...
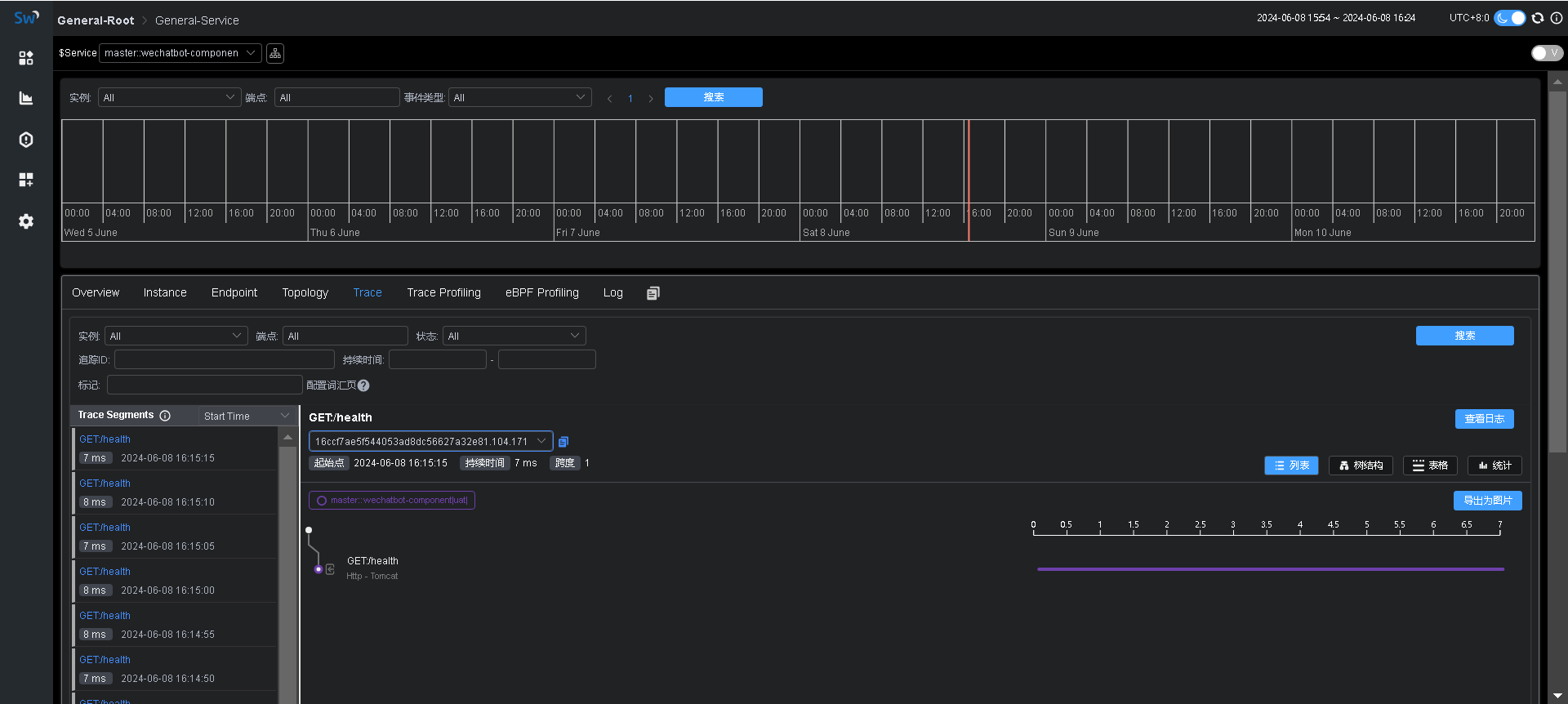
【SkyWalking】启用apm-trace-ignore-plugin追踪忽略插件
背景 使用Agent采集追踪数据的时候,想排除某些路径,比如健康检查等,这样可以减少上报的数据,也可以去除一些不必要的干扰数据。 加载插件 在agent/optional-plugins目录中有个apm-trace-ignore-plugin-${version}.jar插件&…...
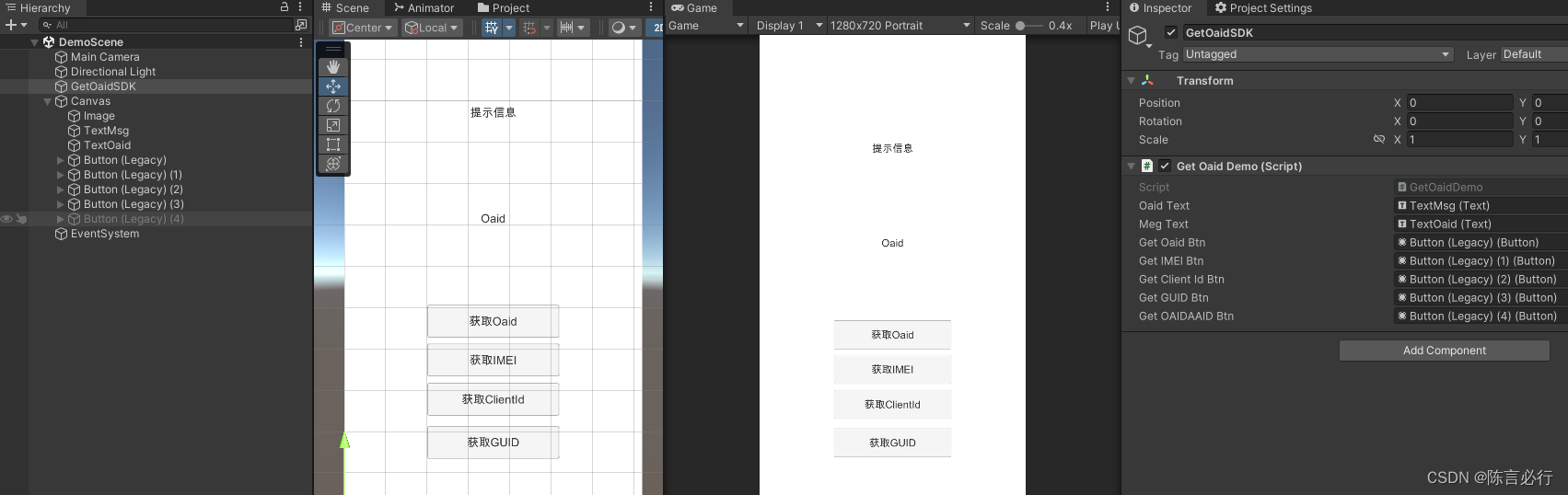
独立游戏之路 -- 获取OAID提升广告收益
Unity 之 获取手机:OAID、IMEI、ClientId、GUID 前言一、Oaid 介绍1.1 Oaid 说明1.2 移动安全联盟(MSA) 二、站在巨人的肩膀上2.1 本文实现参考2.2 本文实现效果2.3 本文相关插件 三、Unity 中获取Oaid3.1 查看实现源码3.2 工程配置3.3 代码实现3.4 场景搭建 四、总…...
反转链表 (oj题)
一、题目链接 https://leetcode.cn/problems/reverse-linked-list/submissions/538124207 二、题目思路 1.定义三个指针,p1先指向NULL p2指向头结点 p3指向第二个结点 2.p2的next指向p1。然后移动指针,p1来到p2的位置,p2来到p3的位置&…...
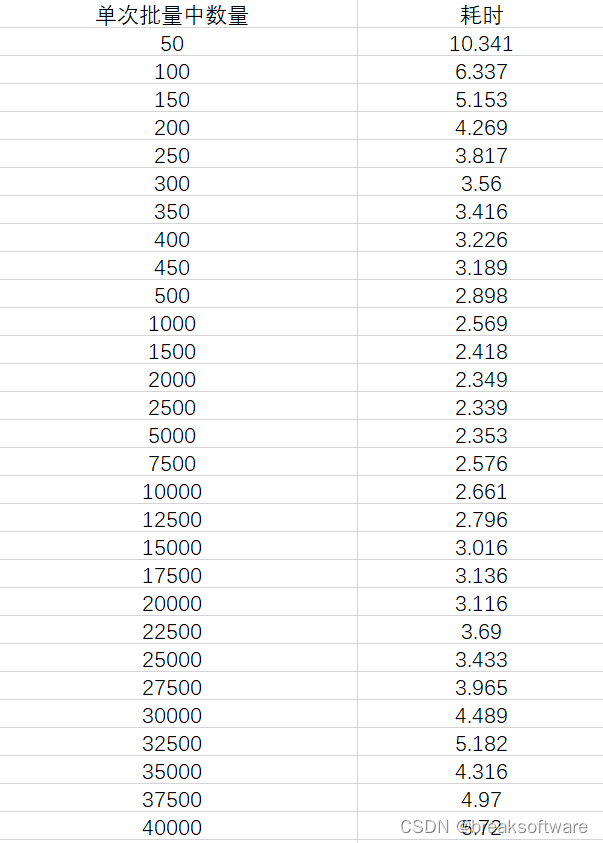
Mysql使用中的性能优化——批量插入的规模对比
在《Mysql使用中的性能优化——单次插入和批量插入的性能差异》中,我们观察到单次批量插入的数量和耗时呈指数型关系。 这个说明,不是单次批量插入的数量越多越好。本文我们将通过实验测试出本测试案例中最佳的单次批量插入数量。 结论 本案例中约每次…...

TCP为什么握手是三次,而挥手是四次
TCP(传输控制协议)使用三次握手(3WHS)来建立一个可靠的连接,并使用四次挥手(4WHS)来终止连接。以下是每个步骤的详细解释: 三次握手(3WHS)建立连接ÿ…...

前端面试题大合集9----TypeScript
目录 一、TypeScript 中静态类型的概念及其好处 二、如何在 TypeScript 的接口中定义可选属性? 三、解释 TypeScript 中联合类型的概念并提供示例 四、TypeScript 中的类型断言是什么? 五、TS中泛型是什么? 六、解释 TypeScript 中的“…...

Linux:动态库和静态库的编译与使用
目录 1.前言 2.静态链接库 3.静态链接库生成步骤 4.静态链接库的使用 5.动态链接库 6.动态链接库生成步骤 7.动态链接库的使用 8.动态链接库无法加载 9.解决动态链接库无法加载问题 前言 在《MinGW:从入门到链接库》博客中简单介绍了如何编译动态链接库和静态链接库…...
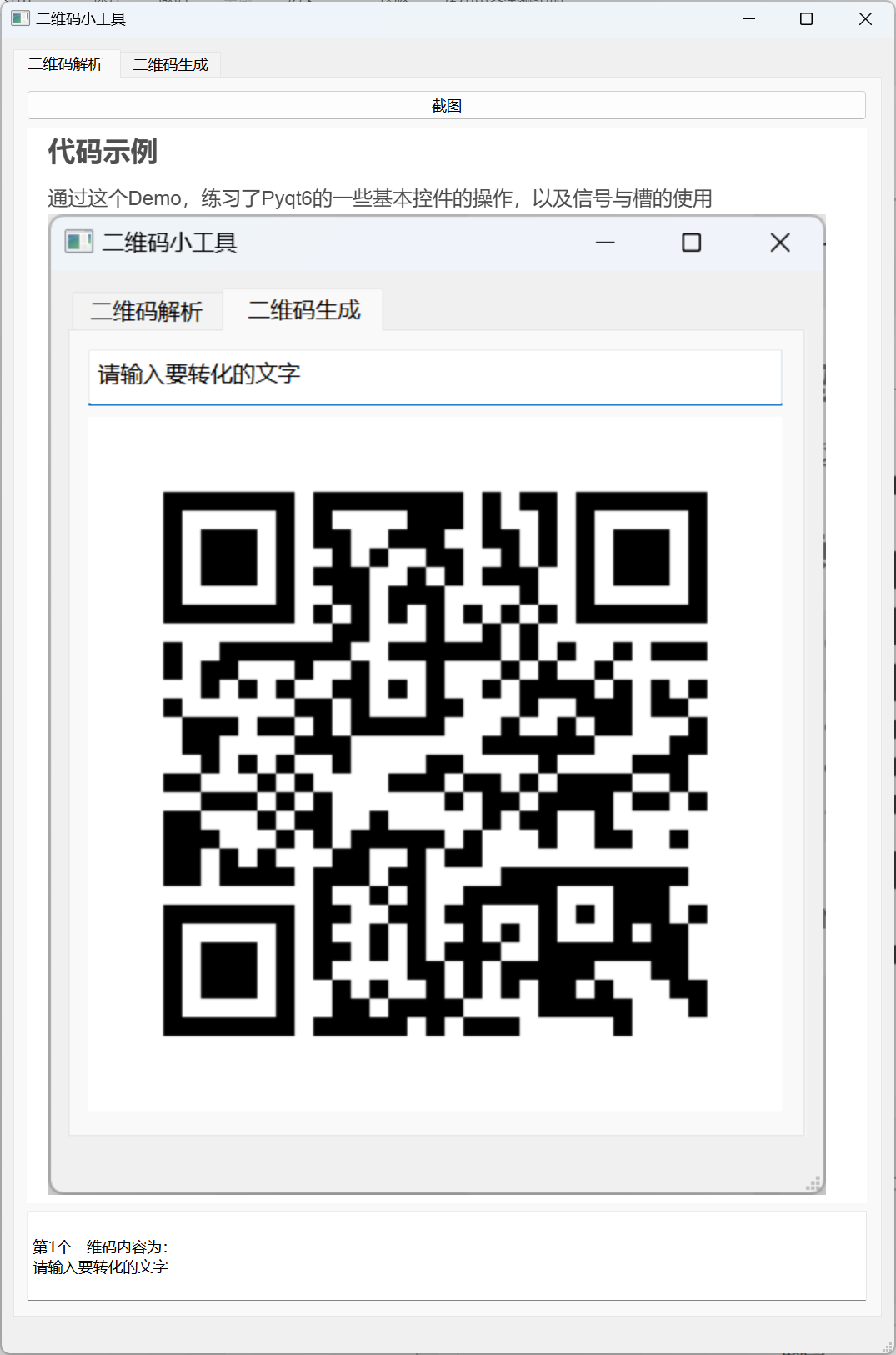
【Pyqt6 学习笔记】DIY一个二维码解析生成小工具
文章目录 Pycharm 配置QtDesignerPyUIC基本模板 代码示例依赖包main.pyscreen_shot_module.pyuntitled.pyuntitled.ui Pycharm 配置 摘自PyQT6的从零开始在Pycharm中配置与使用——蹦跑的蜗牛 pip install PyQt6 PyQt6-toolsQtDesigner File -> Settings -> External …...

关于xilinx srio ip复位问题
关于xilinx srio ip复位问题 语言 :Verilg HDL 、VHDL EDA工具: Vivado 关于xilinx srio ip复位问题一、引言二、FPGA 之间 srio通信复位处理复位时序不同步:SRIO 模块未正确初始化:等待复位完成的时间不足:SRIO 配置…...
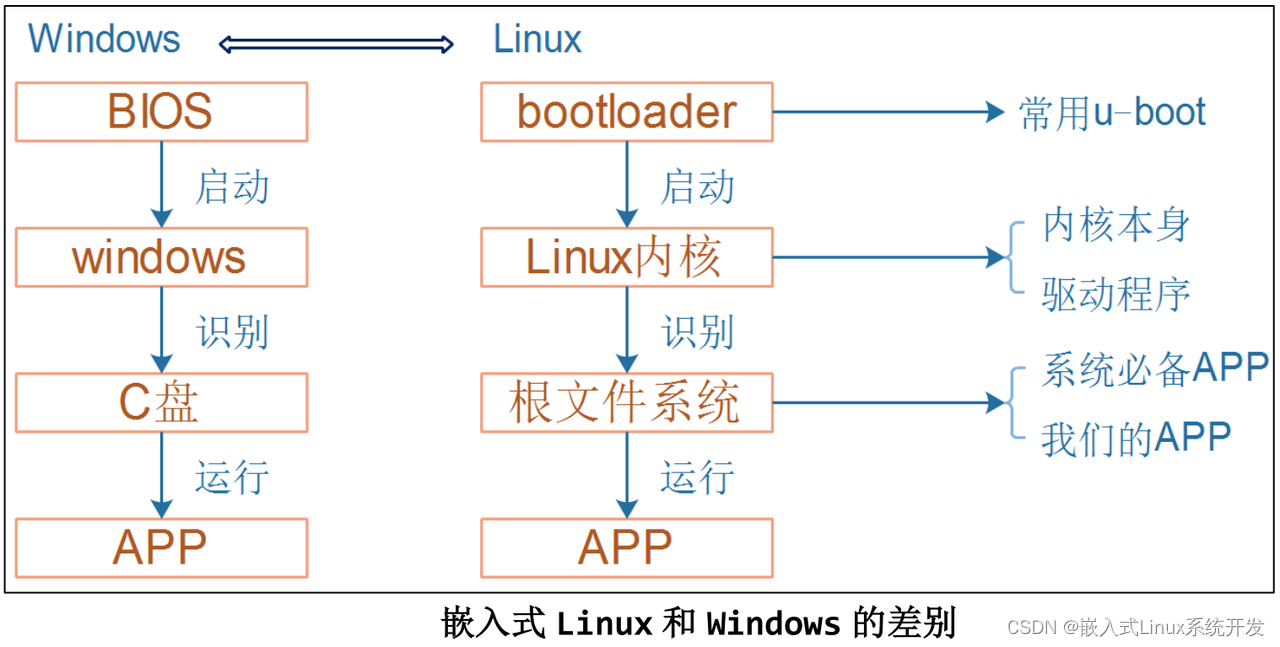
04 uboot 编译与调试
新手不需要详细掌握 uboot,只需要知道它是一个什么东西即可,工作中也只是改一些参数而已。 1、uboot 是什么 Linux 系统要启动就必须需要一个 bootloader 程序,也就说芯片上电以后先运行一段 bootloader 程序。这段 bootloader 程序会先初始化 DDR 等外设,然后将 Linux 内…...

【机器学习】机器学习与医疗健康在智能诊疗中的融合应用与性能优化新探索
文章目录 引言机器学习与医疗健康的基本概念机器学习概述监督学习无监督学习强化学习 医疗健康概述疾病预测诊断辅助个性化治疗方案制定 机器学习与医疗健康的融合应用实时健康监测数据预处理特征工程 疾病预测与优化模型训练模型评估 诊断辅助与优化深度学习应用 个性化治疗方…...
在线OJ项目测试(selenium+Junit5)
目录 在线OJ项目测试的思维导图 在线OJ的UI自动化测试 测试一:检查未登录时的页面访问以及一些未登录时的非法操作 测试二:测试注册界面 测试三:测试登录界面 测试四:测试题目列表界面 测试五:测试题目详情界面…...

计算机系统基础笔记(12)——控制
前言 在持续输出ing 一、条件码 1.处理器状态(x86-64,部分的) 当前程序的执行信息 ◼ 临时数据 ◼ 运行时栈的位置(栈顶) ◼ 当前代码控制点的位置(即将要执行的指令地址) ◼ 最近一次指令执…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
