Leetcode 回溯详解
回溯法
回溯法有“通用解题法”之称,用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。
在包含问题的所有解的解空间树中,按照深度优先搜索(DFS))的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。

解题步骤
- 针对所给问题,定义问题的解空间
- 确定易于搜索的解空间结构
- 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
子集树与排列树
下面的两棵解空间树是回溯法解题时常遇到的两类典型的解空间树,子集树与排列树
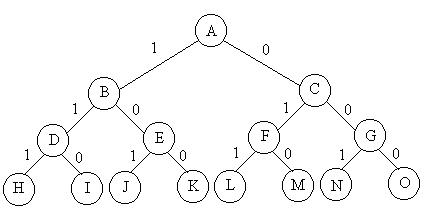
子集树
当所给问题是从n个元素的集合S中找出S满足某种性质的子集时,相应的解空间树称为子集树。例如从n个物品的0-1背包问题所相应的解空间树是一棵子集树,这类子集树通常有2n{2^n}2n个叶结点,其结点总个数为2n+1−1{2 ^{n+1}- 1}2n+1−1。遍历子集树的算法需O(2n{2^n}2n)计算时间
用回溯法搜索子集树的一般算法可描述为:
/*** output(x) 记录或输出得到的可行解x* constraint(t) 当前结点的约束函数* bount(t) 当前结点的限界函数* @param t t为当前解空间的层数*/
void backtrack(int t){if(t >= n)output(x);elsefor (int i = 0; i <= 1; i++) {x[t] = i;if(constraint(t) && bount(t))backtrack(t+1);}
}
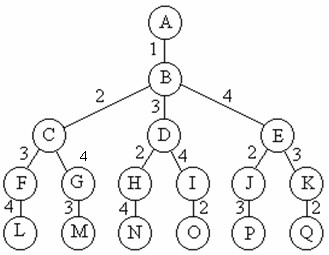
排列树
当所给问题是确定n个元素满足某种性质的排列时,相应的解空间树称为排列树。例如旅行售货员问题的解空间树是一棵排列树,这类排列树通常有n!{n!}n!个叶结点。遍历子集树的算法需O(n!{n!}n!)计算时间
用回溯法搜索排列树的一般算法可描述为:
/*** output(x) 记录或输出得到的可行解x* constraint(t) 当前结点的约束函数* bount(t) 当前结点的限界函数* @param t t为当前解空间的层数*/
void backtrack(int t){if(t >= n)output(x);elsefor (int i = t; i <= n; i++) {swap(x[t], x[i]);if(constraint(t) && bount(t))backtrack(t+1);swap(x[t], x[i]);}
}
Leetcode真题
电话号码的字母组合
解题思路:
经典排列树,按节点遍历
private String[] voc = new String[]{"","*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
List<String> res = new ArrayList();
public List<String> letterCombinations(String digits) {if (digits == null || digits.length() == 0) {return res;}backtrack(digits, 0, new StringBuffer());return res;
}public void backtrack(String digits, int index, StringBuffer s) {if (index == digits.length()) {res.add(s.toString());return;}int i = digits.charAt(index) - '0';for (char c : voc[i].toCharArray()) {s.append(c);backtrack(digits, index + 1, s);s.deleteCharAt(s.length() - 1);}
}
括号生成
解题思路:
排列树,按节点遍历
- 回溯结束条件:左括号数 = 右括号数 = 总数
- 左括号数<总数, 字符串加入左括号
- 右括号数<总数 且 左括号数>右括号数,字符串加入右括号
List<String> res = new ArrayList<>();
public List<String> generateParenthesis(int n) {backtrack(n, 0, 0, "");return res;
}void backtrack(int n, int l, int r, String str) {if (l == n && r == n) {res.add(str);}if (l < n) {backtrack(n, l + 1, r, str + "(");}if (r < n && l > r) {backtrack(n, l, r + 1, str + ")");}
}
N皇后
解题思路:
子集树,按节点遍历
- 回溯结束条件:所有层数放置完毕
- 每列循环遍历,当满足非冲突条件时(列,主对角线,副对角线不冲突)
- 放置该行的皇后
- 执行下一级回溯
两点位于同一对角线时,行列值相加/相减的值相等
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {if (n <= 0) {return res;}backtrack(0, n, new int[n]);return res;
}/*** output(x) 记录或输出得到的可行解x* constraint(t) 当前结点的约束函数** @param t t为当前解空间的层数* @param n 总层数* @param queens 结果集,下标为行号,值为列号*/
void backtrack(int t, int n, int[] queens) {if (t >= n) {output(res, n, queens);return;} else {for (int j = 0; j < n; j++) {if (constraint(t, j, n, queens)) {queens[t] = j;backtrack(t + 1, n, queens);}}}
}/*** 检查是否存在冲突(列,主对角线,副对角线)* 两点位于同一对角线时,行列值相加/相减的值相等*/
boolean constraint(int t, int j, int n, int[] queens) {for (int i = 0; i < t; i++) {if (queens[i] == j || i - queens[i] == t - j || i + queens[i] == t + j) {return false;}}return true;
}void output(List<List<String>> res, int n, int[] queens) {List<String> list = new ArrayList<>();for (int i = 0; i < n; i++) {char[] chars = new char[n];Arrays.fill(chars, '.');chars[queens[i]] = 'Q';list.add(new String(chars));}res.add(list);
}
参考资料:
- 回溯法的解题步骤与例子解析
- leetcode
- 深度优先搜索
相关文章:
Leetcode 回溯详解
回溯法 回溯法有“通用解题法”之称,用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。 在包含问题的所有解的解空间树中,按照深度优先搜索(DFS))的策略,从根结点出发深度探索解空间树。当探索…...
AI_Papers:第一期
2023.02.06—2023.02.12 文摘词云 Top Papers Subjects: cs.CL 1.Multimodal Chain-of-Thought Reasoning in Language Models 标题:语言模型中的多模式思维链推理 作者:Zhuosheng Zhang, Aston Zhang, Mu Li, Hai Zhao, George Karypis, Alex Sm…...
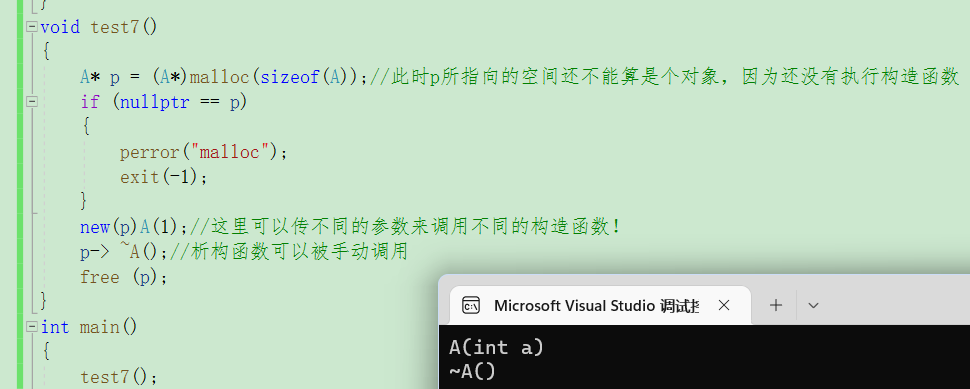
C/C++内存管理
C/C内存管理C/C内存分布C语言中内存管理的方式:malloc/calloc/realloc/freeC内存管理方式内置类型自定义类型operator new 与operator deletenew和delete的实现原理内置类型自定义类型定位new表达式(placement-new)new/delete与malloc/free的区别C/C内存分布 我们先…...
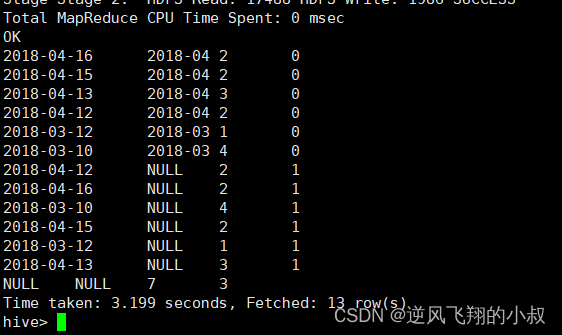
【大数据hive】hive 函数使用详解
一、前言 在任何一种编程语言中,函数可以说是必不可少的,像mysql、oracle中,提供了很多内置函数,或者通过自定义函数的方式进行定制化使用,而hive作为一门数据分析软件,随着版本的不断更新迭代,…...
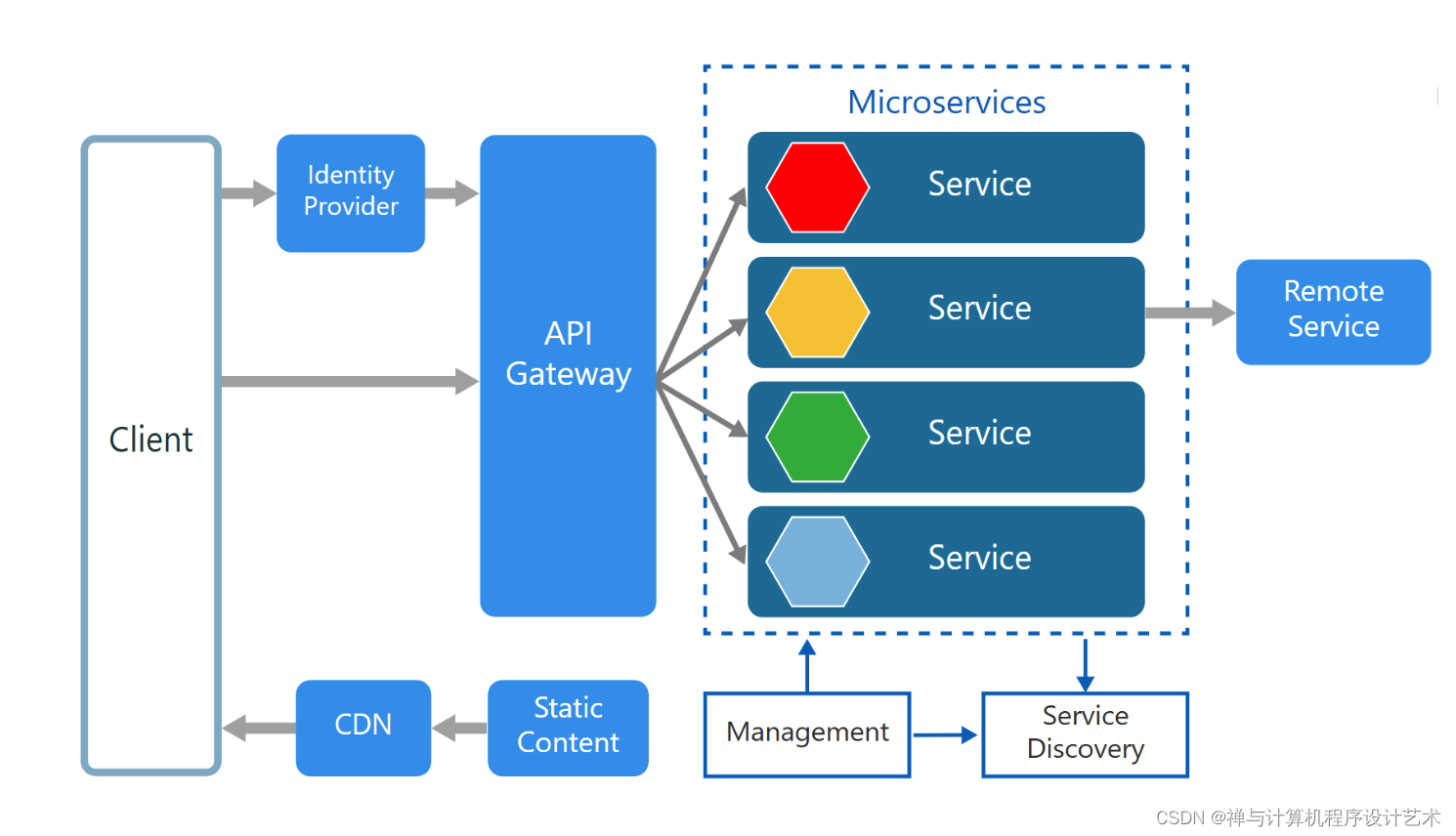
彻底搞懂分布式系统服务注册与发现原理
目录 引入服务注册与发现组件的原因 单体架构 应用与数据分离...

安卓Camera2用ImageReader获取NV21源码分析
以前如何得到Camera预览流回调 可以通过如下方法,得到一路预览回调流 Camera#setPreviewCallbackWithBuffer(Camera.PreviewCallback),可以通过如下方法,设置回调数据的格式,比如 ImageFormat.NV21 Camera.Parameters#setPreview…...

24. 两两交换链表中的节点
文章目录题目描述迭代法递归法参考文献题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入&a…...

linux006之帮助命令
linux帮助命令简介: linux的命令是非常多的,光靠人是记不住的,在工作中一般都会去网上查,这是有外网的情况下,如果项目中不允许访问外网,那么linux的帮助命令就可以派上用场了, linux帮助命令是…...

【C++初阶】十三、模板进阶(总)|非类型模板参数|模板的特化|模板分离编译|模板总结(优缺点)
目录 一、非类型模板参数 二、模板的特化 2.1 模板特化概念 2.2 函数模板特化 2.3 类模板特化 2.3.1 全特化 2.3.2 偏特化 三、模板分离编译 四、模板总结(优缺点) 前言:之前模板初阶并没有把 C模板讲完,因为当时没有接触…...
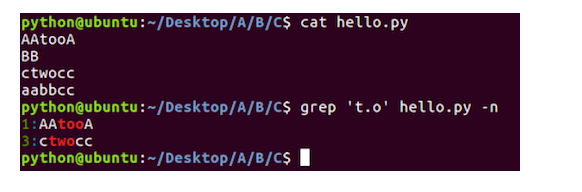
Linux之文本搜索命令
文本搜索命令学习目标能够知道文本搜索使用的命令1. grep命令的使用命令说明grep文本搜索grep命令效果图:2. grep命令选项的使用命令选项说明-i忽略大小写-n显示匹配行号-v显示不包含匹配文本的所有行-i命令选项效果图:-n命令选项效果图:-v命令选项效果图:3. grep命令结合正则表…...

微信小程序Springboot 校园拼车自助服务系统java
系统管理员: 管理员账户管理:在线对管理员的账户信息进行管理,包括对管理员信息的增加修改以及密码的修改等。 站内新闻管理:在后台对站内新闻信息进行发布,并能够对站内新闻信息进行删除修改等。 论坛版块管理&#x…...

【Unity3D 常用插件】Haste插件
一,Haste介绍 Haste插件是一款针对 Unity 3D 的 Everthing软件,可以实现基于名称快速定位对象的功能。Unity 3D 编辑器也自带了搜索功能,但是在 project视图 和 Hierarchy视图 中的对象需要分别查找,不支持模糊匹配。Haste插件就…...

【c++面试问答】全局变量和局部变量的区别
问题 C中的全局变量和局部变量有什么区别? 注:内容全部参考自文末的参考资料 全局变量和局部变量的区别 可以从以下4个角度来区分: 区别全局变量局部变量作用域全局作用域局部作用域内存分配全局变量在静态数据区静态局部变量在静态数据区…...

Java List集合
6 List集合 List系列集合:添加的元素是有序,可重复,有索引 ArrayList: 添加的元素是有序,可重复,有索引LinkedList: 添加的元素是有序,可重复,有索引Vector :是线程安全的ÿ…...

linux服务器挂载硬盘/磁盘
1. 查看机器所挂硬盘个数及分区情况:fdisk -l可以看出来目前/dev/vda 目前有300G可用.内部有两个分区(/dev/vda1,/dev/vda2)。2. 格式化磁盘格式化磁盘命令为【mkfs.磁盘类型格式 目录路径组成】查看磁盘文件格式:df -T格式化磁盘…...

Java 抽象类
文章目录1、抽象方法和抽象类2、抽象类的作用当编写一个类时,常常会为该类定义一些方法,用于描述该类的行为方式,这些方法都有具体的方法体。但在某些情况下,某个基类只是知道其子类应该包含那些方法,但不知道子类是如…...
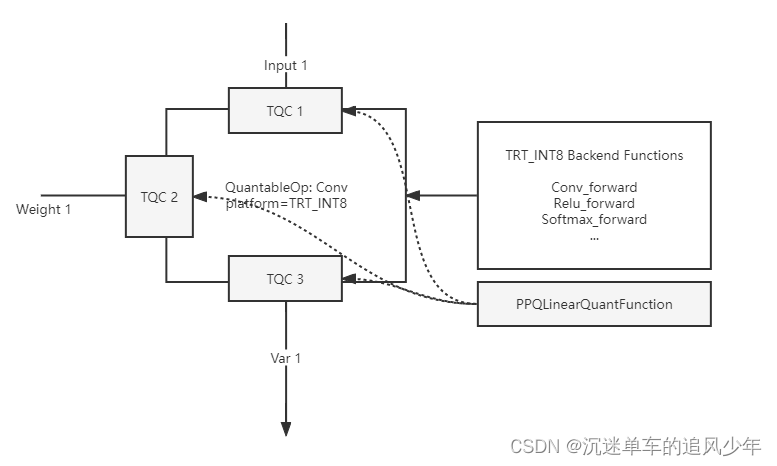
OpenPPL PPQ量化(5):执行引擎 源码剖析
目录 PPQ Graph Executor(PPQ 执行引擎) PPQ Backend Functions(PPQ 算子库) PPQ Executor(PPQ 执行引擎) Quantize Delegate (量化代理函数) Usage (用法示例) Hook (执行钩子函数) 前面四篇博客其实就讲了下面两行代码: ppq_ir load_onnx_graph(onnx_impor…...
【脚本开发】运维人员必备技能图谱
脚本(Script)语言是一种动态的、解释性的语言,依据一定的格式编写的可执行文件,又称作宏或批处理文件。脚本语言具有小巧便捷、快速开发的特点;常见的脚本语言有Windows批处理脚本bat、Linux脚本语言shell以及python、…...
N字形变换-力扣6-java
一、题目描述将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:P A H NA P L S I I GY I R之后,你的输出需要从左往右逐行读…...
)
概论_第5章_中心极限定理1__定理2(棣莫弗-拉普拉斯中心极限定理)
在概率论中, 把有关论证随机变量和的极限分布为正态分布的一类定理称为中心极限定理称为中心极限定理称为中心极限定理。 本文介绍独立同分布序列的中心极限定理。 一 独立同分布序列的中心极限定理 定理1 设X1,X2,...Xn,...X_1, X_2, ...X_n,...X1,X2,...Xn…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...