概论_第5章_中心极限定理1__定理2(棣莫弗-拉普拉斯中心极限定理)
在概率论中, 把有关论证随机变量和的极限分布为正态分布的一类定理称为中心极限定理称为中心极限定理称为中心极限定理。
本文介绍独立同分布序列的中心极限定理。
一 独立同分布序列的中心极限定理
定理1 设X1,X2,...Xn,...X_1, X_2, ...X_n,...X1,X2,...Xn,... 是独立同分布的随机变量序列, 且具有相同数学期望和方差,E(Xi)=μ,D(Xi)=σ2(i=1,2,...)E(X_i)=\mu, D(X_i)=\sigma^2(i=1,2, ...)E(Xi)=μ,D(Xi)=σ2(i=1,2,...), 记随机变量 Yn=Y_n=Yn=∑i=1nXi−nμnσ\frac{\sum\limits_{i=1}^{n}X_i-n\mu}{\sqrt{n}\sigma}nσi=1∑nXi−nμ 的分布函数为Fn(x)F_n(x)Fn(x), 则对于任意实数 xxx,
limn→∞Fn(x)=limn→∞P{Yn⩽x}=\lim\limits_{n \rightarrow \infty}F_n(x) =\lim\limits_{n \rightarrow \infty}P\{Y_n \leqslant x\} =n→∞limFn(x)=n→∞limP{Yn⩽x}= limn→∞P\lim\limits_{n \rightarrow \infty}Pn→∞limP{\{{ ∑i=1n−nμnσ\frac{\sum\limits_{i=1}^{n}-n\mu}{ \sqrt{n}\sigma}nσi=1∑n−nμ }\}}
=∫−∞x12πe−t22dt=Φ(x)=\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt=\Phi(x)=∫−∞x2π1e−2t2dt=Φ(x),
由这一定理可知以下结论:
1.
当n充分大时, 独立同分布的随机变量之和 Zn=∑i=1nXiZ_n=\sum\limits_{i=1}^{n}X_iZn=i=1∑nXi的分布近似于正态分布 N(nμ,nσ2)N(n\mu, n\sigma^2)N(nμ,nσ2).
中心极限定理告诉我们, 不论X1,X2,...,Xn,...X_1,X_2, ..., X_n,...X1,X2,...,Xn,...同服从什么分布, 当n充分大时, 其和ZnZ_nZn 近似服从正态分布.
2.
考虑 独立同分布的随机变量X1,X2,...,Xn,...X_1, X_2,..., X_n,...X1,X2,...,Xn,... 的平均值 X‾=1n∑i=1nXi\overline X = \frac{1}{n}\sum\limits_{i=1}^{n}X_iX=n1i=1∑nXi, 有
它的标准化随机变量为 X‾−μσ/n\frac{\overline X - \mu}{\sigma/ \sqrt{n}}σ/nX−μ 即为上述YnY_nYn, 因此 X‾−μσ/n\frac{\overline X - \mu}{\sigma/ \sqrt{n}}σ/nX−μ 的分布函数即是上述的Fn(x)F_n(x)Fn(x), 因而有
limn→∞Fn(x)=∫−∞x12πe−t22dt=Φ(x)\lim\limits_{n \rightarrow \infty}F_n(x) =\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt = \Phi(x)n→∞limFn(x)=∫−∞x2π1e−2t2dt=Φ(x).
由此可见, 当n充分大时, 独立同分布随机变量的平均值X‾=1n∑i=1nXi\overline X = \frac{1}{n}\sum\limits_{i=1}^{n}X_iX=n1i=1∑nXi 的分布近似于正态分布 NNN(μ,σ2n)(\mu, \frac{\sigma^2}{n})(μ,nσ2), 这是独立同分布中心极限定理的另一表达形式。
二 棣莫弗—拉普拉斯中心极限定理
此定理是 定理1 的特殊情况。
定理2(棣—拉中心极限定理)
设随机变量ZnZ_nZn是n次独立重复试验中事件A发生的次数, p是事件A发生的概率, 则对于任意实数 xxx
limn→∞\lim\limits_{n \rightarrow \infty}n→∞limP{\{{Zn−npnp(1−p)⩽x\frac{Z_n-np}{\sqrt{np(1-p)}}\leqslant xnp(1−p)Zn−np⩽x}\}}=∫−∞x12πe−t22dt=Φ(x)=\int_{- \infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt = \Phi(x)=∫−∞x2π1e−2t2dt=Φ(x).
由棣—拉中心极限定理,得到下列结论:
1.
在贝努利试验中, 若事件A发生的概率为p, 设ZnZ_nZn为n次独立重复试验中事件A发生的频数, 则当n充分大时, ZnZ_nZn 近似服从N(np,np(1−p))N(np, np(1-p))N(np,np(1−p)).
2.
在贝努利试验中, 若事件A发生的概率为p, Znn\frac{Z_n}{n}nZn 为n次独立重复试验中事件A 发生的频率, 则当n充分大时, Znn\frac{Z_n}{n}nZn 近似服从N(p,p(1−p)n)N(p, \frac{p(1-p)}{n})N(p,np(1−p)).
三 例题
- 设随机变量X~B(100, 0.2), Φ(x)\Phi(x)Φ(x) 为标准正态分布函数, 已知Φ(2.5)=0.9938\Phi(2.5)=0.9938Φ(2.5)=0.9938, 应用 中心极限定理, 可得 P{20⩽x⩽3020\leqslant x \leqslant 3020⩽x⩽30} ≈\approx≈ ___________。
解: X ~ B(100, 0.2), np=20, npq = 16, 则P{20 ⩽x⩽30\leqslant x \leqslant 30⩽x⩽30} = P{20−2016⩽X−2016⩽30−2016}P\{{\frac{20-20}{\sqrt{16}} \leqslant \frac{X-20}{\sqrt{16}} \leqslant \frac{30-20}{\sqrt{16}}}\}P{1620−20⩽16X−20⩽1630−20} (这一步用到定理2)
≈Φ(30−204)−Φ(20−204)=Φ(2.5)−Φ(0)=0.9938−0.5=0.4938\approx \Phi(\frac{30-20}{4}) - \Phi(\frac{20-20}{4}) = \Phi(2.5) - \Phi(0) = 0.9938-0.5 = 0.4938≈Φ(430−20)−Φ(420−20)=Φ(2.5)−Φ(0)=0.9938−0.5=0.4938.
答案为 0.4938。
相关文章:
)
概论_第5章_中心极限定理1__定理2(棣莫弗-拉普拉斯中心极限定理)
在概率论中, 把有关论证随机变量和的极限分布为正态分布的一类定理称为中心极限定理称为中心极限定理称为中心极限定理。 本文介绍独立同分布序列的中心极限定理。 一 独立同分布序列的中心极限定理 定理1 设X1,X2,...Xn,...X_1, X_2, ...X_n,...X1,X2,...Xn…...
详细解读503服务不可用的错误以及如何解决503服务不可用
文章目录1. 问题引言2. 什么是503服务不可用错误3 尝试解决问题3.1 重新加载页面3.2 检查该站点是否为其他人关闭3.3 重新启动设备3.3 联系网站4. 其他解决问的方法1. 问题引言 你以前遇到过错误503吗? 例如,您可能会收到消息,如503服务不可…...

【前端vue2面试题】2023前端最新版vue模块,高频17问(上)
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:博主收集的关于vue2面试题(上) 目录 vue2面试题 1、$route 和 $router的区别 2、一个…...
数据库(三):多版本并发控制MVCC,行锁的衍生版本,记录锁,间隙锁, Next-Key锁(邻键锁)
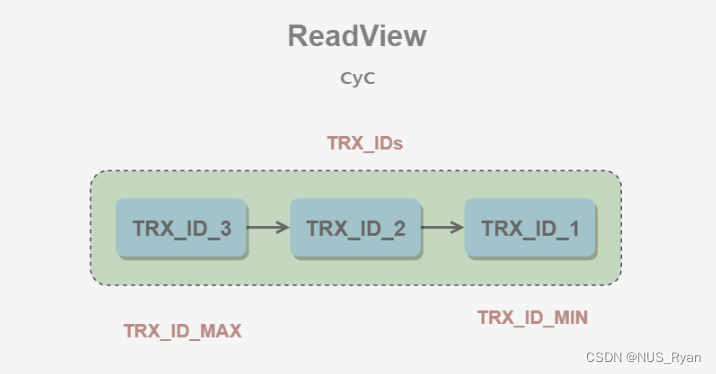
文章目录前言一、MVCC以及MVCC的缺点1.1 MVCC可以为数据库解决什么问题1.2 MVCC的基本思想1.3 版本号1.4 Undo日志1.5 ReadView1.6 快照读和当前读1.6.1 快照读1.6.2 当前读二、记录锁三、间隙锁四、邻键锁总结前言 一、MVCC以及MVCC的缺点 MVCC,即多版本并发控制…...
c# 自定义隐式转换与运算符重载
用户定义的显式和隐式转换运算符 参考代码 用户定义的显式和隐式转换运算符 - 提供对不同类型的转换 | Microsoft Learn 代码例程 using System;public readonly struct Digit {private readonly byte digit;public Digit(byte digit){if (digit > 9){throw new Argumen…...
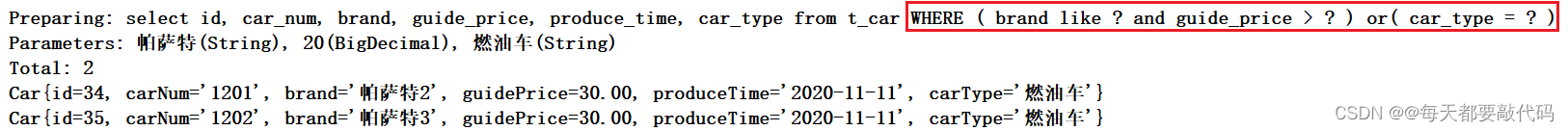
【MyBatis】| MyBatis的逆向⼯程
目录 一:MyBatis的逆向⼯程 1. 逆向⼯程配置与⽣成 2. 测试生成的逆向⼯程 一:MyBatis的逆向⼯程 (1)所谓的逆向⼯程是:根据数据库表逆向⽣成Java的pojo类,SqlMapper.xml⽂件,以及Mapper接⼝…...

Python|每日一练|哈希表|罗马数字|图算法|圆周率|单选记录:给定数列和|罗马数字转整数|计算圆周率
1、要求编写函数fn(a,n) 求aaaaaa⋯aa⋯aa(n个a)之和,fn须返回的是数列和(算法初阶) 要求编写函数fn(a,n) 求aaaaaa⋯aa⋯aa(n个a)之和,fn须返回的是数列和。 从控制台输入正整数a和n的值(两…...

分布式之分布式事务V2
写在前面 本文一起来看下分布式环境下的事务问题,即我们经常听到的分布式事务问题。想要解决分布式事务问题,需要使用到分布式事务相关的协议,主要有2PC即两阶段提交协议,TCC(try-confirm-cancel)…...

算法笔记(二)—— 认识N(logN)的排序算法
递归行为的时间复杂度估算 整个递归过程是一棵多叉树,递归过程相当于利用栈做了一次后序遍历。 对于master公式,T(N)表明母问题的规模为N,T(N/b)表明每次子问题的规模,a为调用次数,加号后面表明,除去调用之…...

最长湍流子数组——滚动窗口,双指针,暴力求解
978. 最长湍流子数组难度中等216收藏分享切换为英文接收动态反馈给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。更正式地来说,当 arr 的子数组 A[i]…...

45.在ROS中实现global planner(1)
前文move_base介绍(4)简单介绍move_base的全局路径规划配置,接下来我们自己实现一个全局的路径规划 1. move_base规划配置 ROS1的move_base可以配置选取不同的global planner和local planner, 默认move_base.cpp#L70中可以看到是…...
Java中导入、导出Excel——HSSFWorkbook 使用
一、介绍 当前B/S模式已成为应用开发的主流,而在企业办公系统中,常常有客户这样子要求:你要把我们的报表直接用Excel打开(电信系统、银行系统)。或者是:我们已经习惯用Excel打印。这样在我们实际的开发中,很多时候需要…...

c#数据结构-列表
列表 数组可以管理大量数组,但缺点是无法更变容量。 创建小了不够用,创建大了浪费空间。 无法预测需要多少大小的时候,可能范围越大,就会浪费越多的空间。 所以,你可能会想要一种可以扩容的东西,代替数组…...
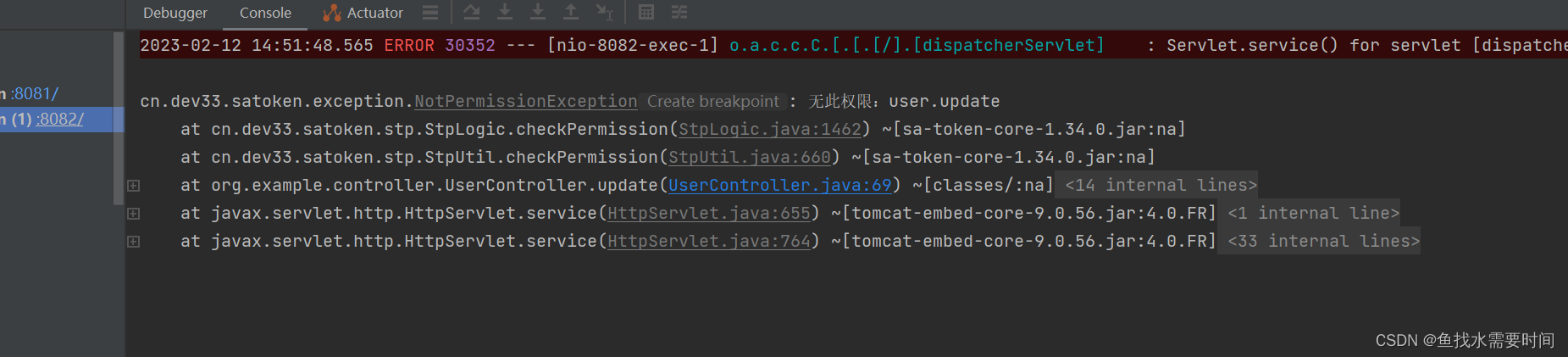
Sa-Token实现分布式登录鉴权(Redis集成 前后端分离)
文章目录1. Sa-Token 介绍2. 登录认证2.1 登录与注销2.2 会话查询2.3 Token 查询3. 权限认证3.1 获取当前账号权限码集合3.2 权限校验3.3 角色校验4. 前后台分离(无Cookie模式)5. Sa-Token 集成 Redis6. SpringBoot 集成 Sa-Token6.1 创建项目6.2 添加依…...

leaflet显示高程
很多地图软件都能随鼠标移动动态显示高程。这里介绍一种方法,我所得出的。1 下载高程数据一般有12.5m数据下载,可惜精度根本不够,比如mapbox的免费在线的,或者91卫图提供百度网盘打包下载的,没法用,差距太大…...
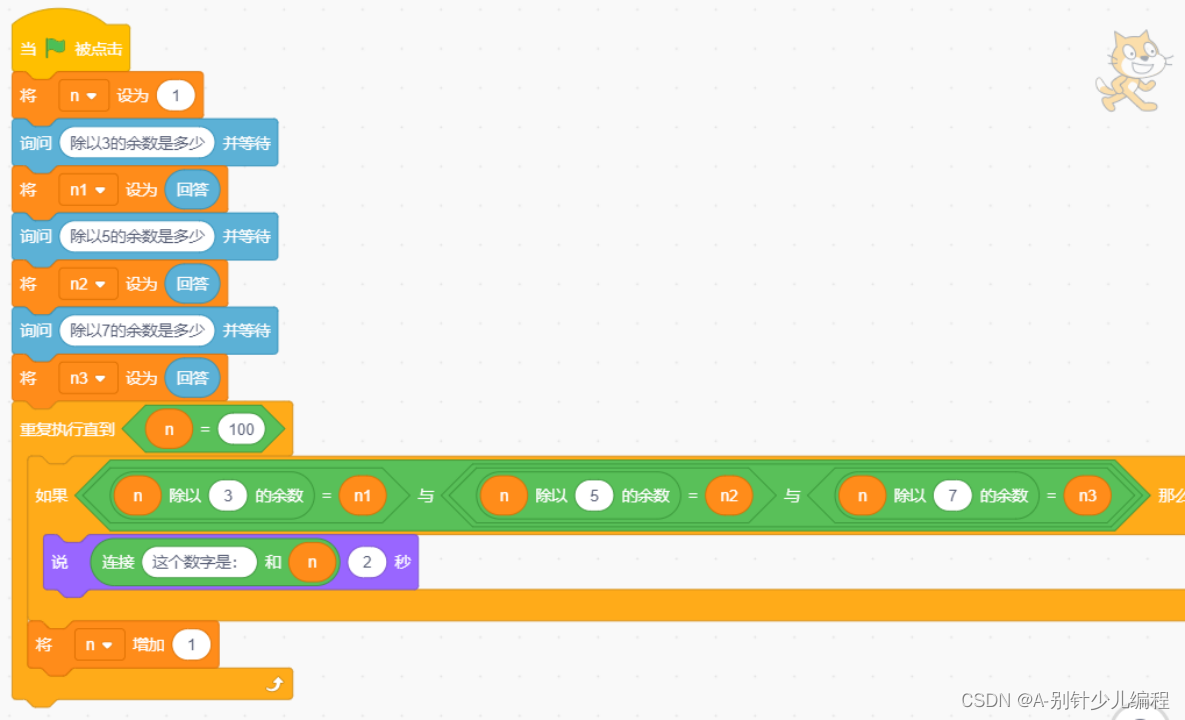
电子学会2022年12月青少年软件编程(图形化)等级考试试卷(三级)答案解析
目录 一、单选题(共25题,共50分) 二、判断题(共10题,共20分) 三、编程题(共3题,共30分) 青少年软件编程(图形化)等级考试试卷(三级) 一、单选题(共25题,共50分) 1. 默认小猫角色…...

ubuntu 驱动更新后导致无法进入界面
**问题描述: **安装新ubuntu系统后未禁止驱动更新导致无法进入登录界面。 解决办法: 首先在进入BIOS中,修改设置以进行命令行操作,然后卸载已有的系统驱动,最后安装新的驱动即可。 开机按F11进入启动菜单栏…...
解决访问GitHub时出现的“您的连接不是私密连接”的问题!
Content问题描述解决办法问题描述 访问github出现您的连接不是私密连接问题,无法正常访问,如下图所示: 解决办法 修改hosts文件。hosts文件位于:C:\Windows\System32\drivers\etc\hosts 首先在https://www.ipaddress.com/查找两…...
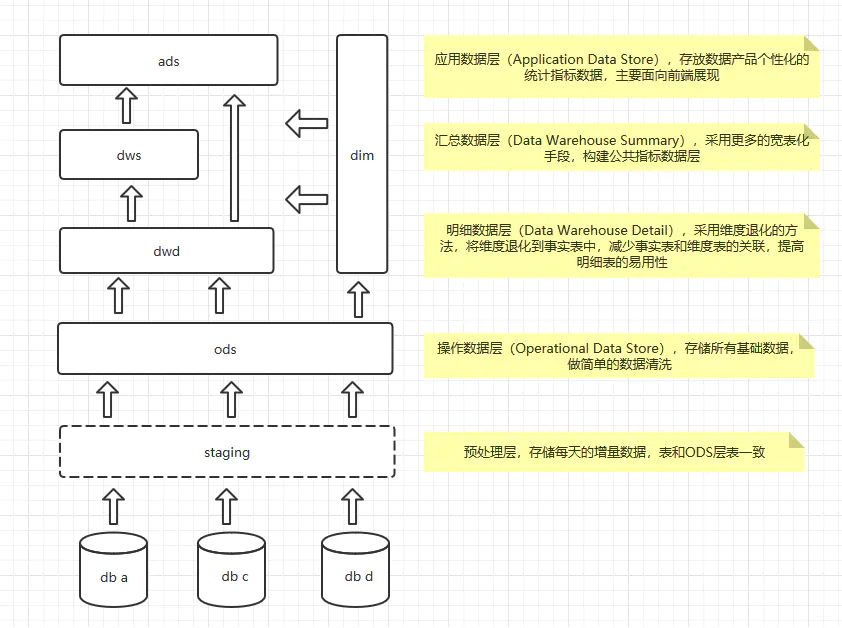
初识数据仓库
一、什么是数据仓库数据库 --> OLTP:(on-line transaction processing)翻译为联机事务处理记录某类业务事件的发生,如购买行为,银行交易行为,当行为产生后,系统会记录是谁在何时何地做了何事…...

FilenameUtils工具类部分源码自研
FilenameUtils工具类部分源码自研getExtension(orgFileName)源码如下逐行分析getExtension(orgFileName)源码如下 public class FilenameUtils {public static int indexOfExtension(String fileName) throws IllegalArgumentException {if (fileName null) {return -1;} els…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
