Python|每日一练|哈希表|罗马数字|图算法|圆周率|单选记录:给定数列和|罗马数字转整数|计算圆周率
1、要求编写函数fn(a,n)
求a+aa+aaa++⋯+aa⋯aa(n个a)之和,fn须返回的是数列和(算法初阶)
要求编写函数fn(a,n) 求a+aa+aaa++⋯+aa⋯aa(n个a)之和,fn须返回的是数列和。 从控制台输入正整数a和n的值(两个值都不超过9),并输出fn(a,n)的结果值。
选项代码:
def fun(a,n):s = 1sum = 1for i in range(1,n):s = 1 + s*10sum+=sy = a *sumprint(y)
def main():while(1):a = int(input('请输入a:'))if a>9 or a<0:print('a的值输入错误,请重新输入:')else:breakwhile(1):n = int(input('请输入n:'))if n>9 or n<0:print('n的值输入错误,请重新输入:')else:breakfun(a,n)
if __name__ == '__main__':main()2、罗马数字转整数(哈希表,数学)
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
- I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
- X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
- C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
(原题目中示例的输入、输出与题意相反,已修正)。
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V = 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
- 1 <= num <= 3999
选项代码:
class Solution:def romanToInt(self, s: str) -> int:units = [["M", 1000, 1],["CM", 900, 2],["D", 500, 1],["CD", 400, 2],["C", 100, 1],["XC", 90, 2],["L", 50, 1],["XL", 40, 2],["X", 10, 1],["IX", 9, 2],["V", 5, 1],["IV", 4, 2],["I", 1, 1]]end = len(s)start = 0i = 0r = 0while i < len(units):unit = units[i][0]value = units[i][1]step = units[i][2]if end-start >= step and s[start:start+step] == unit:r += valuestart += stepelse:i += 1return r
# %%
s = Solution()
print(s.romanToInt('MCMXCIV'))
3、python 编写函数计算圆周率(图算法,算法高阶)
计算圆周率。存在圆心在直角坐标系原点且半径为 1 的圆及其外切正方形。为计算方便,仅考虑位于第一象限的四分之一正方形和四分之一圆。随机生成该四分之一正方形中一系列点,散布于四分之一圆内比例即为圆周率四分之一。散步点越多,结果越精确,耗时也越长。
以下程序实现了这一功能,请你填补空白处内容:
from random import random
from math import sqrt
N=eval(input("请输入次数:"))
K=0
for i in range(1,N+1):x,y=random(),random()dist =sqrt(x**2+y**2)_____________________;
pi=4*(K/N)
print("圆周率值:{}".format(pi))
完整选项代码:
from random import random
from math import sqrt
N=eval(input("请输入次数:"))
K=0for i in range(1,N+1):x,y=random(),random()dist =sqrt(x**2+y**2)if dist <= 1.0:K = K + 1
pi=4*(K/N)
print("圆周率值:{}".format(pi))相关文章:

Python|每日一练|哈希表|罗马数字|图算法|圆周率|单选记录:给定数列和|罗马数字转整数|计算圆周率
1、要求编写函数fn(a,n) 求aaaaaa⋯aa⋯aa(n个a)之和,fn须返回的是数列和(算法初阶) 要求编写函数fn(a,n) 求aaaaaa⋯aa⋯aa(n个a)之和,fn须返回的是数列和。 从控制台输入正整数a和n的值(两…...

分布式之分布式事务V2
写在前面 本文一起来看下分布式环境下的事务问题,即我们经常听到的分布式事务问题。想要解决分布式事务问题,需要使用到分布式事务相关的协议,主要有2PC即两阶段提交协议,TCC(try-confirm-cancel)…...

算法笔记(二)—— 认识N(logN)的排序算法
递归行为的时间复杂度估算 整个递归过程是一棵多叉树,递归过程相当于利用栈做了一次后序遍历。 对于master公式,T(N)表明母问题的规模为N,T(N/b)表明每次子问题的规模,a为调用次数,加号后面表明,除去调用之…...

最长湍流子数组——滚动窗口,双指针,暴力求解
978. 最长湍流子数组难度中等216收藏分享切换为英文接收动态反馈给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。更正式地来说,当 arr 的子数组 A[i]…...

45.在ROS中实现global planner(1)
前文move_base介绍(4)简单介绍move_base的全局路径规划配置,接下来我们自己实现一个全局的路径规划 1. move_base规划配置 ROS1的move_base可以配置选取不同的global planner和local planner, 默认move_base.cpp#L70中可以看到是…...
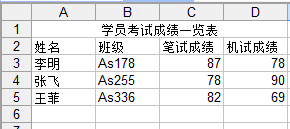
Java中导入、导出Excel——HSSFWorkbook 使用
一、介绍 当前B/S模式已成为应用开发的主流,而在企业办公系统中,常常有客户这样子要求:你要把我们的报表直接用Excel打开(电信系统、银行系统)。或者是:我们已经习惯用Excel打印。这样在我们实际的开发中,很多时候需要…...

c#数据结构-列表
列表 数组可以管理大量数组,但缺点是无法更变容量。 创建小了不够用,创建大了浪费空间。 无法预测需要多少大小的时候,可能范围越大,就会浪费越多的空间。 所以,你可能会想要一种可以扩容的东西,代替数组…...
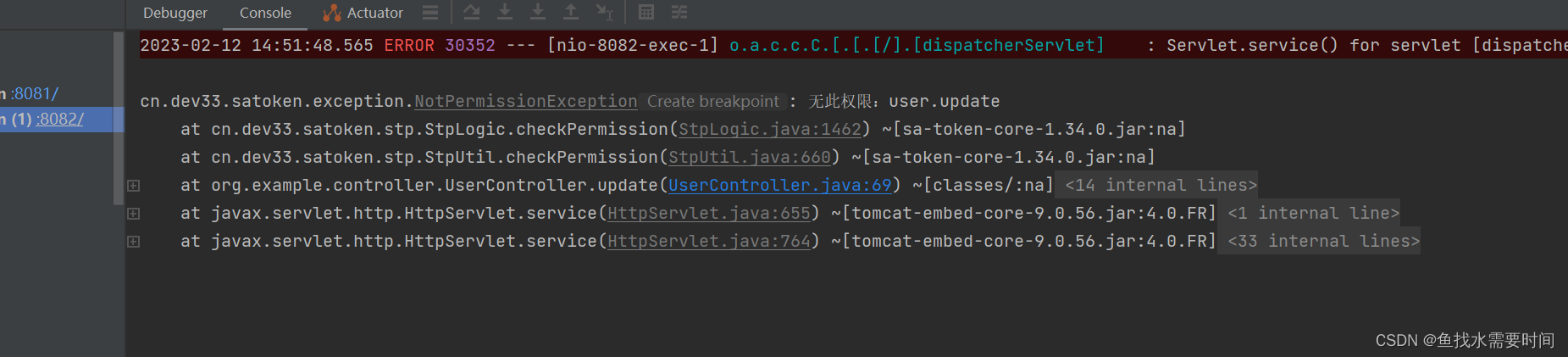
Sa-Token实现分布式登录鉴权(Redis集成 前后端分离)
文章目录1. Sa-Token 介绍2. 登录认证2.1 登录与注销2.2 会话查询2.3 Token 查询3. 权限认证3.1 获取当前账号权限码集合3.2 权限校验3.3 角色校验4. 前后台分离(无Cookie模式)5. Sa-Token 集成 Redis6. SpringBoot 集成 Sa-Token6.1 创建项目6.2 添加依…...

leaflet显示高程
很多地图软件都能随鼠标移动动态显示高程。这里介绍一种方法,我所得出的。1 下载高程数据一般有12.5m数据下载,可惜精度根本不够,比如mapbox的免费在线的,或者91卫图提供百度网盘打包下载的,没法用,差距太大…...
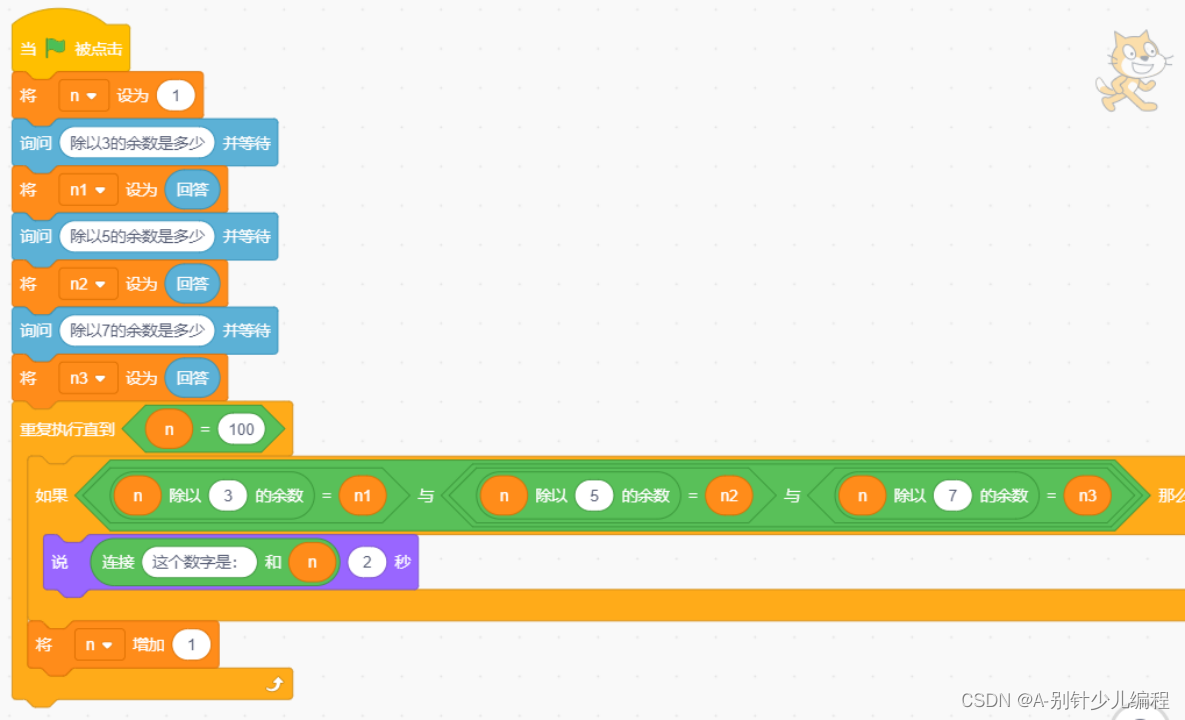
电子学会2022年12月青少年软件编程(图形化)等级考试试卷(三级)答案解析
目录 一、单选题(共25题,共50分) 二、判断题(共10题,共20分) 三、编程题(共3题,共30分) 青少年软件编程(图形化)等级考试试卷(三级) 一、单选题(共25题,共50分) 1. 默认小猫角色…...

ubuntu 驱动更新后导致无法进入界面
**问题描述: **安装新ubuntu系统后未禁止驱动更新导致无法进入登录界面。 解决办法: 首先在进入BIOS中,修改设置以进行命令行操作,然后卸载已有的系统驱动,最后安装新的驱动即可。 开机按F11进入启动菜单栏…...
解决访问GitHub时出现的“您的连接不是私密连接”的问题!
Content问题描述解决办法问题描述 访问github出现您的连接不是私密连接问题,无法正常访问,如下图所示: 解决办法 修改hosts文件。hosts文件位于:C:\Windows\System32\drivers\etc\hosts 首先在https://www.ipaddress.com/查找两…...
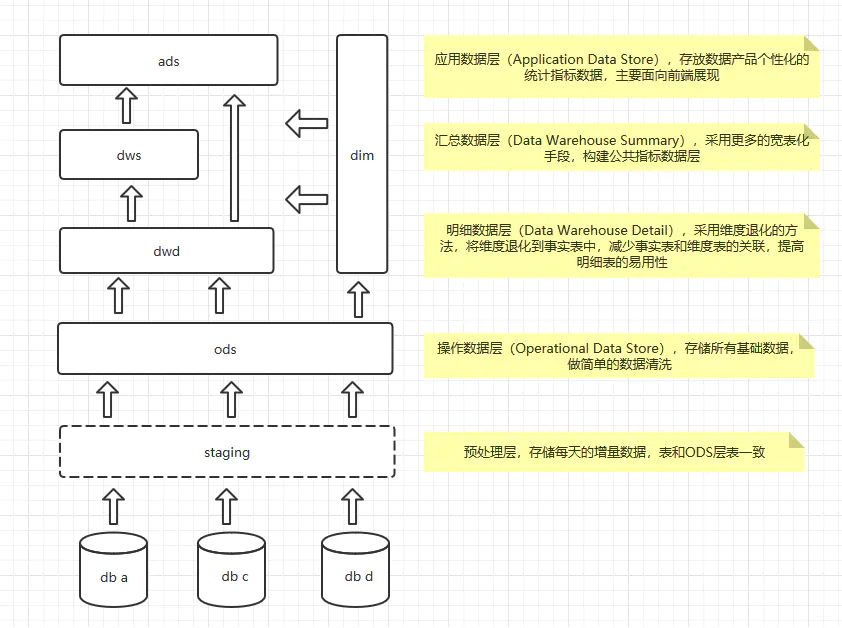
初识数据仓库
一、什么是数据仓库数据库 --> OLTP:(on-line transaction processing)翻译为联机事务处理记录某类业务事件的发生,如购买行为,银行交易行为,当行为产生后,系统会记录是谁在何时何地做了何事…...

FilenameUtils工具类部分源码自研
FilenameUtils工具类部分源码自研getExtension(orgFileName)源码如下逐行分析getExtension(orgFileName)源码如下 public class FilenameUtils {public static int indexOfExtension(String fileName) throws IllegalArgumentException {if (fileName null) {return -1;} els…...
【前端领域】3D旋转超美相册(HTML+CSS)
世界上总有一半人不理解另一半人的快乐。 ——《爱玛》 目录 一、前言 二、本期作品介绍 3D旋转相册 三、效果展示 四、详细介绍 五、编码实现 index.html style.css img 六、获取源码 公众号获取源码 获取源码?私信?关注?点赞&…...
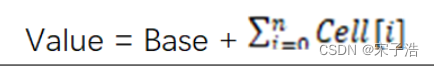
Java——聊聊JUC中的原子变量类
文章目录: 1.什么是原子变量类? 2.AtomicInteger(基本类型原子变量类) 3.AtomicIntegerArray(数组类型原子变量类) 4.AtomicMarkableReference(引用类型原子变量类) 5.AtomicInteger…...

elasticsearch索引与搜索初步
ES支持cURL交互,使用http请求完成索引和搜索操作,最基本的格式如下:创建索引我们可以使用PUT方法创建索引,通过指定“索引”、“类型”、“文档ID”锁定文档,通过参数指定文档的数据。红色部分的路由分别指定了“索引”…...

【Python】多线程与多进程学习笔记
本文是一篇学习笔记,学习内容主要来源于莫凡python的文档:https://mofanpy.com/tutorials/python-basic/threading/thread 多线程 线程基本结构 开启子线程的简单方式如下: import threadingdef thread_job():print(This is a thread of %…...

MySQL基础知识点
1.在Linux上安装好MySQL8.0之后,默认数据目录的具体位置是什么?该目录下都保存哪些数据库组件?在目录/usr/sbin、/usr/bin、/etc、/var/log 分别保存哪些组件? 答:默认数据目录:/var/lib/mysql。保存有mysq…...

代码随想录算法训练营第五十九天| 583. 两个字符串的删除操作、72. 编辑距离
Leetcode - 583dp[i][j]代表以i-1结尾的words1的子串 要变成以j-1结尾的words2的子串所需要的次数。初始化: "" 变成"" 所需0次 dp[0][0] 0, ""变成words2的子串 需要子串的长度的次数,所以dp[0][j] j, 同理,dp[i][0] …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
)
Android多媒体——音/视频数据播放(十八)
在媒体数据完成解码并准备好之后,播放流程便进入了最终的呈现阶段。为了确保音视频内容能够顺利输出,系统需要首先对相应的播放设备进行初始化。只有在设备初始化成功后,才能真正开始音视频的同步渲染与播放。这一过程不仅影响播放的启动速度,也直接关系到播放的稳定性和用…...
MySQL 数据库深度剖析:事务、SQL 优化、索引与 Buffer Pool
在当今数据驱动的时代,数据库作为数据存储与管理的核心,其性能与可靠性至关重要。MySQL 作为一款广泛使用的开源数据库,在众多应用场景中发挥着关键作用。在这篇博客中,我将围绕 MySQL 数据库的核心知识展开,涵盖事务及…...
