一些简单却精妙的算法
文章目录
- 1.树状数组
- 2.红黑树
- 3.星星打分
- 4.欧几里得算法
- 5.快速幂
- 6.并查集
在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。
1.树状数组
int lowbit(int x)
{ return x&-x;
}
树状数组里的这个,太精妙了,树状数组使区间求和复杂度降低到了log(n),发明这段代码的人一定是个天才,而这个lowbit恰恰是最精妙的一部分,可以准确的找到我们需要加的部分,巧妙的利用了计算机的位运算。
2.红黑树
defun rbt-balance (tree) "Balance the rbtree list TREE." (pcase tree (`(B (R (R ,a ,x ,b) ,y ,c) ,z ,d) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B (R ,a ,x (R ,b ,y ,c)) ,z ,d) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B ,a ,x (R (R ,b ,y ,c) ,z ,d)) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B ,a ,x (R ,b ,y (R ,c ,z ,d))) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (_ tree))) (defun rbt-insert- (x s) "Auxilary function of rbt-insert." (pcase s (`nil `(R nil ,x nil)) (`(,color ,a ,y ,b) (cond ((< x y) (rbt-balance `(,color ,(rbt-insert- x a) ,y ,b))) ((> x y) (rbt-balance `(,color ,a ,y ,(rbt-insert- x b)))) (t s))) (_ (error "Expected tree: %S" s)))) (defun rbt-insert (x s) "Insert S to rbtree X." (pcase (rbt-insert- x s) (`(,_ ,a ,y ,b) `(B ,a ,y ,b)) (_ (error "Internal error: %S" s))))
3.星星打分
function getRating(rating) { if(rating > 5 || rating < 0) throw new Error('数字不在范围内'); return '★★★★★☆☆☆☆☆'.substring(5 - rating, 10 - rating );
}
这种实现方式之所以精妙,是因为它利用了字符串的固定模式和 substring 方法的灵活性来生成不同数量的星星,而不需要使用循环或额外的逻辑来逐个添加或删除星星。这种方法简洁且高效,特别是在需要频繁生成星级评分表示时。
然而,这段代码也有局限性,它假设评分总是整数,并且只支持0到5的评分范围。如果需要支持小数评分或更广泛的评分范围,这段代码将需要相应的调整。
4.欧几里得算法
function gcd(a, b) { return b ? gcd(b, a % b) : a;
}
这种递归实现的欧几里得算法非常简洁且高效。它利用了数学上的一个性质:两个整数的最大公约数与它们的余数和较小数的最大公约数相同。即 gcd(a, b) = gcd(b, a % b)。
5.快速幂
function fastPower(b, n) { if (n === 0) return 1; const result = fastPower(b, Math.floor(n / 2)); return n % 2 === 0 ? result * result : b * result * result;
用于高效地计算 b 的 n 次方。快速幂算法特别适用于计算大幂次的情况,因为它将幂次的计算复杂度从 O(n) 降低到 O(log n)。
6.并查集
int find(int x){ x==parent[x]?:find(parent[x]);
}
并查集(Union-Find)数据结构中的 find 函数的简洁实现。
递归查找:find 函数通过递归的方式查找元素 x 的根节点。递归会在元素与其父节点不同时,继续查找父节点的父节点,直到找到一个元素其父节点是它自己的元素,即根节点。
路径压缩:代码中的三元运算符 ?: 实现了路径压缩技术。当 x 不是其根节点时(即 x != parent[x]),find 函数会调用自身并传入 parent[x] 作为参数。在递归返回的过程中,每个节点的父节点指针都被更新为最终的根节点,这样可以减少后续查找操作的深度。
相关文章:

一些简单却精妙的算法
文章目录 1.树状数组2.红黑树3.星星打分4.欧几里得算法5.快速幂6.并查集 在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。 1.树状数组 int lowbit(int x) { …...

git多账号使用报错:You don‘t have permissions to push to “xxx/xxxx“ onGitHub. Would
git多账号使用报错:You don’t have permissions to push to “xxx/xxxx” onGitHub. Would 有的时候我们有两个甚至多个git账号(公司的git账号和自己的github),为了不混淆提交,我们需要在提交之前查看自己的git账号必…...
2023年12月真题C语言软件编程等级考试三级(含详细解析答案))
中国电子学会(CEIT)2023年12月真题C语言软件编程等级考试三级(含详细解析答案)
中国电子学会(CEIT)考评中心历届真题(含解析答案) C语言软件编程等级考试三级 2023年12月 编程题五道 总分:100分一、因子问题(20分) 任给两个正整数N、M,求一个最小的正整数a,使得a和(M-a)都是N的因子。 时间限制: 10000ms 内存限制: 65536kb 输入 包括两个整…...

多线程爬取百度图片
爬取网页图片 import urllib.parse import requests import os import time from concurrent.futures import ThreadPoolExecutorheaders {"User-Agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/125.0.0.0…...

RK3568-修改fiq-debugger调试串口
瑞芯微SDK默认将uart2_m0作为调试串口,以下方法将调试串口修改为uart5_m1。修改bootloader 修改/OK3568-linux-source/rkbin/tools/ddrbin_param.txt文件,5表示串口5。1表示复用m1。执行./ddrbin_tool ddrbin_param.txt ../bin/rk35/rk3568_ddr_1560MHz_v1.11.bin命令修改ub…...

我们离成功有多远呢?只要能完成自己阶段性的目标就算是一次成功
做起一个账号,带好一个团队,经营好一家公司,似乎这些都能叫成功,成功的定义可大可小,而我认为只要能完成自己阶段性的目标就算是一次成功,毕竟每个人学历、背景、阅历、资源、认知都不同,很难同…...

Golang 避坑指南
文章目录 1. Channel 与 Goroutine 泄露1.1 发送不接收1.2 接收不发送1.3 nil channel2. 跳出 for-switch 或 for-select 3.for 迭代变量3.1 闭包中的for迭代变量3.2 for range 迭代变量 4. 循环内的 defer5.defer 函数的参数值6.nil interface 和 nil interface 值7.结构体指针…...
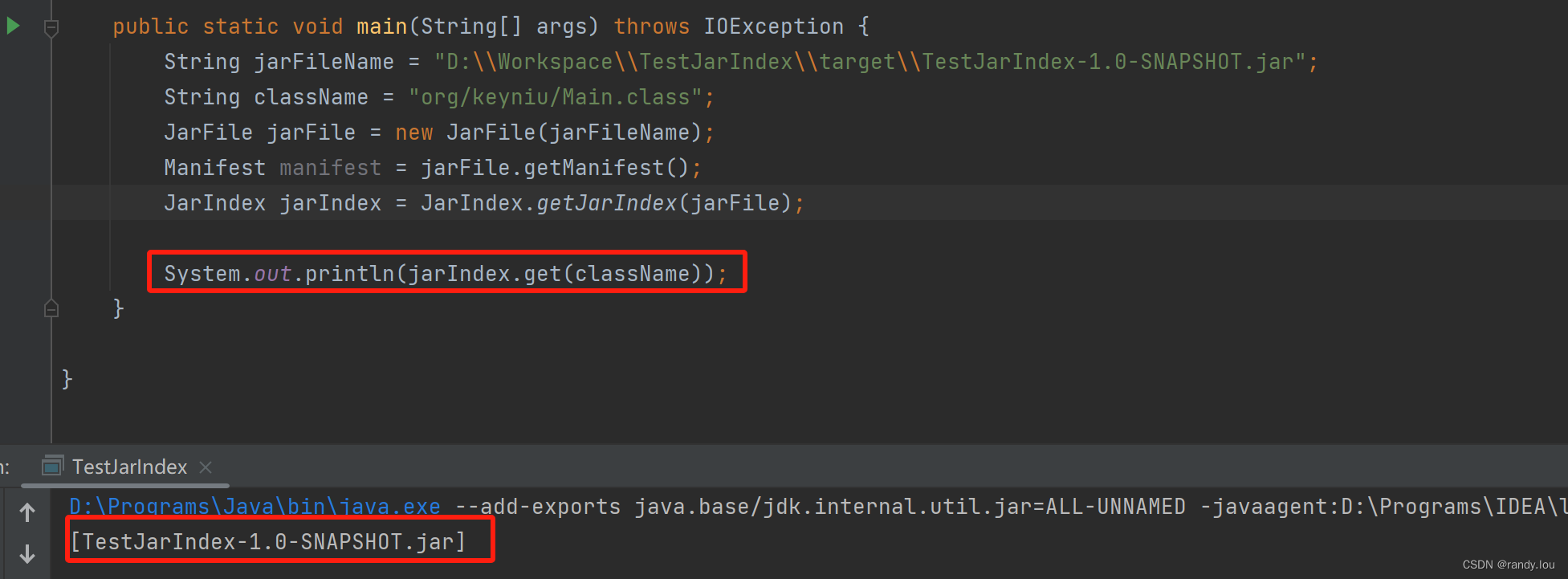
Java核心: JarIndex的使用
在讲解Java类加载器的时候,我们发现URLClassLoader加载类或资源时通过访问ClassPath下的每一个路径,来确定类是否存在的,假设我们执行的命令是这样的 java -classpath D:\DiveInSpring\target\classes;C:\lib\spring-expression.jar;C:\lib\…...

1052 卖个萌(测试点1,2)
solution 想要输出\需要用\\才能输出,即 cout << "Are you kidding me? \\/" << endl;测试点1,2:输入序号小于1的非法情况 #include<iostream> #include<string> #include<map> using namespace…...

Vue 3与ESLint、Prettier:构建规范化的前端开发环境
title: Vue 3与ESLint、Prettier:构建规范化的前端开发环境 date: 2024/6/11 updated: 2024/6/11 publisher: cmdragon excerpt: 这篇文章介绍了如何在Vue 3项目中配置ESLint和Prettier以统一代码风格,实现代码规范性与可读性的提升。通过设置规则、解…...

npm安装依赖过慢
今天在使用npm安装taro框架的依赖时,速度慢到吐血,使用了淘宝镜像源依然很慢,安装一个多小时没反应,最后清理了缓存再次安装速度就快很多了,因此解决方法大致有两种: 使用淘宝镜像源 原域名: ht…...

计算机毕业设计 | SpringBoot+vue的教务管理系统
1,绪论 1.1 项目背景 在这个资讯高度发展的时代,资讯管理变革已经是一个更为宽泛、更为全面的潮流。为了保证中国的可持续发展,随着信息化技术的不断进步,教务管理体系也在不断完善。与此同时,伴随着信息化的飞速发展…...

深入探索深度学习的验证集:必要还是可选?
深入探索深度学习的验证集:必要还是可选? 在深度学习项目的设计和实施过程中,数据通常被划分为训练集、测试集,以及有时的验证集。尽管在一些研究中,我们可能看到只有训练集和测试集被使用,验证集的作用及…...

初识C++ · 反向迭代器简介
目录 前言 反向迭代器的实现 前言 继模拟实现了list和vector之后,我们对迭代器的印象也是加深了许多,但是我们实现的都是正向迭代器,还没有实现反向迭代器,那么为什么迟迟不实现呢?因为难吗?实际上还好。…...

fastapi学习前置知识点
前置知识点 FastApi:一个用于构建API的现代、快速(高性能)的web框架。 FastApi是建立在Pydantic和Starlette基础上,Pydantic是一个基于Python类型提示来定义数据验证、序列化和文档的库。Starlette是一种轻量级的ASGI框架/工具包…...

机器学习常见知识点 1:Baggin集成学习技术和随机森林
文章目录 1、集成学习a.BaggingBagging的工作原理1. 自助采样(Bootstrap Sampling)2. 训练多个基学习器3. 聚合预测 Bagging的优点Bagging的缺点应用场景 b.Boosting 2、决策树3、随机森林随机森林的核心概念1. 集成学习2. 决策树 构建随机森林的步骤1. …...

容器(Docker)安装
centos安装Docker sudo yum remove docker* sudo yum install -y yum-utils#配置docker的yum地址 sudo yum-config-manager \ --add-repo \ http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo#安装指定版本 - 可以根据实际安装版本 sudo yum install -y docke…...

前端JS必用工具【js-tool-big-box】学习,获取当前浏览器向上滚动还是向下滚动,获取当前距离顶部和底部的距离
这一小节,我们说一下 js-tool-big-box 添加的最新工具方法,在日常前端开发工作中,如果网页很长,我们就需要获取当前浏览器是在向上滚动,还是向下滚动。如果向上滚动,滚动到0的时候呢,需要做一些…...

【python】flask 框架
python flask 框架 flask是一个轻量级的python后端框架 (Django, tornado, flask) 官网:欢迎来到 Flask 的世界 — Flask中文文档(3.0.x) 安装:pip install Flask -i https://pypi.douban.com 常识: http,默认端口号为80; https,默认端口号…...

Word中插入Mathtype右编号,调整公式与编号的位置
当你已经将mathtype内置于word后,可以使用右编号快速插入公式 但是往往会出现公式和编号出现的位置或之间的距离不合适 比如我在双栏下插入公式,会发现插入的公式与编号是适用于单栏的 解决办法: 开始->样式->MTDisplayLquation -&g…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
