深入探索深度学习的验证集:必要还是可选?

深入探索深度学习的验证集:必要还是可选?
在深度学习项目的设计和实施过程中,数据通常被划分为训练集、测试集,以及有时的验证集。尽管在一些研究中,我们可能看到只有训练集和测试集被使用,验证集的作用及其重要性经常被新手所忽视或误解。本文将详细探讨验证集的功能、为何它在许多情况下是必不可少的,以及在什么情况下可能被省略。
一、验证集的基本功能
为什么需要验证集?
验证集主要用于模型的性能评估和调整模型参数(如神经网络的层数、节点数、学习率等)。验证集在训练过程中的使用有以下几个关键作用:
- 模型选择:验证集可以用来比较不同模型的性能,帮助选择最佳的模型架构或参数。
- 超参数调整:在模型训练过程中,验证集帮助调整超参数,确保模型不仅仅是对训练数据过度拟合。
- 防止过拟合:通过监控在验证集上的性能,可以及时发现过拟合的现象。如果模型在训练集上表现良好但在验证集上表现不佳,这通常是过拟合的信号。
验证集如何工作?
在训练过程中,模型首先在训练集上学习数据的特征和模式。在各个训练阶段(通常是一个epoch结束后),模型会在验证集上评估,而不会在此数据集上进行进一步的学习。这样可以保证评估结果的客观性和准确性,同时对模型的泛化能力进行了测试。
二、是否可以省略验证集?
虽然验证集在许多深度学习项目中发挥着关键作用,但在某些情况下,研究人员可能会省略它:
1. 资源限制
在数据极其有限的情况下,保留一部分数据作为验证集可能不可行。这种情况下,研究者可能会直接使用测试集来进行模型的选择和调整,尽管这会增加过拟合的风险。
2. 交叉验证
如果采用交叉验证方法,特别是在数据量不足时,可以不单独设置验证集。在交叉验证中,数据被分成多个小组,每个小组轮流作为测试集,其余部分作为训练集,从而每个数据点都被用于训练和验证,增加了评估的稳健性。
3. 使用预训练模型
在使用广泛验证过的预训练模型并进行微调时,有时可以直接使用测试集来调整少量的顶层参数。这种方法在数据集非常特定,且预训练模型已在相似任务上表现良好的情况下使用。
三、总结
虽然在某些特定情况下可以不使用验证集,但在大多数深度学习项目中,验证集是至关重要的。它不仅帮助研究者评估模型的泛化能力,还是调整模型参数、选择最佳模型配置的有力工具。省略验证集可能会带来过拟合和模型泛化能力不足的风险,因此在决定是否使用验证集时,必须权衡这些潜在的风险。
对于深度学习的实践者来说,理解验证集的作用并妥善使用它,是确保模型达到最优性能的关键步骤之一。在设计深度学习实验和模型时,应考虑到验证集的重要性,并根据项目的具体需求和条件作出合理的安排。
相关文章:

深入探索深度学习的验证集:必要还是可选?
深入探索深度学习的验证集:必要还是可选? 在深度学习项目的设计和实施过程中,数据通常被划分为训练集、测试集,以及有时的验证集。尽管在一些研究中,我们可能看到只有训练集和测试集被使用,验证集的作用及…...

初识C++ · 反向迭代器简介
目录 前言 反向迭代器的实现 前言 继模拟实现了list和vector之后,我们对迭代器的印象也是加深了许多,但是我们实现的都是正向迭代器,还没有实现反向迭代器,那么为什么迟迟不实现呢?因为难吗?实际上还好。…...

fastapi学习前置知识点
前置知识点 FastApi:一个用于构建API的现代、快速(高性能)的web框架。 FastApi是建立在Pydantic和Starlette基础上,Pydantic是一个基于Python类型提示来定义数据验证、序列化和文档的库。Starlette是一种轻量级的ASGI框架/工具包…...

机器学习常见知识点 1:Baggin集成学习技术和随机森林
文章目录 1、集成学习a.BaggingBagging的工作原理1. 自助采样(Bootstrap Sampling)2. 训练多个基学习器3. 聚合预测 Bagging的优点Bagging的缺点应用场景 b.Boosting 2、决策树3、随机森林随机森林的核心概念1. 集成学习2. 决策树 构建随机森林的步骤1. …...

容器(Docker)安装
centos安装Docker sudo yum remove docker* sudo yum install -y yum-utils#配置docker的yum地址 sudo yum-config-manager \ --add-repo \ http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo#安装指定版本 - 可以根据实际安装版本 sudo yum install -y docke…...

前端JS必用工具【js-tool-big-box】学习,获取当前浏览器向上滚动还是向下滚动,获取当前距离顶部和底部的距离
这一小节,我们说一下 js-tool-big-box 添加的最新工具方法,在日常前端开发工作中,如果网页很长,我们就需要获取当前浏览器是在向上滚动,还是向下滚动。如果向上滚动,滚动到0的时候呢,需要做一些…...

【python】flask 框架
python flask 框架 flask是一个轻量级的python后端框架 (Django, tornado, flask) 官网:欢迎来到 Flask 的世界 — Flask中文文档(3.0.x) 安装:pip install Flask -i https://pypi.douban.com 常识: http,默认端口号为80; https,默认端口号…...

Word中插入Mathtype右编号,调整公式与编号的位置
当你已经将mathtype内置于word后,可以使用右编号快速插入公式 但是往往会出现公式和编号出现的位置或之间的距离不合适 比如我在双栏下插入公式,会发现插入的公式与编号是适用于单栏的 解决办法: 开始->样式->MTDisplayLquation -&g…...
基于【Lama Cleaner】一键秒去水印,轻松移除不想要的内容!
一、项目背景 革命性的AI图像编辑技术,让您的图片焕然一新!无论水印、logo、不想要的人物或物体,都能被神奇地移除,只留下纯净的画面。操作简单,效果出众,给你全新的视觉体验。开启图像编辑新纪元,尽在掌控! 利用去水印开源工具Lama Cleaner对照片中"杂质"进行去除…...

VMware Workstation Ubuntu server 24 (Linux) 磁盘扩容 挂载硬盘
1 Ubuntu server 关机,新增加磁盘 2 启动ubuntu虚拟机,分区和挂载磁盘 sudo fdisk /dev/sdb #查看磁盘UUID sudo blkid #创建挂载目录 sudo mkdir /mnt/data # sudo vi /etc/fstab /dev/disk/by-uuid/0b440ed0-b28b-4756-beeb-10c585e3d101 /mnt/data ext4 defaults 0 1 #加…...
表的设计与查询
目录 一、表的设计 1.第一范式(一对一) 定义: 示例: 2.第二范式(一对多) 定义: 要求: 示例: 3.第三范式(多对多) 定义: 要求…...

【react】如何合理使用useEffect
useEffect 是 React Hooks API 的一部分,它允许你在函数组件中执行副作用操作,比如数据获取、订阅或者手动更改 DOM。合理使用 useEffect 可以帮助你管理组件的生命周期行为,同时避免不必要的渲染和性能问题。以下是一些关于如何合理使用 useEffect 的建议: 明确依赖项: 当…...

计算机专业英语Computer English
计算机专业英语 Computer English 高等学校计算机英语教材 Contents 目录 Part One Computer hardware and software 计算机硬件和软件----------盖金曙 生家峰 Unit 1 the History of Computers计算机的历史 Unit 2 Computer System计算机系统 Unit 3 Di…...
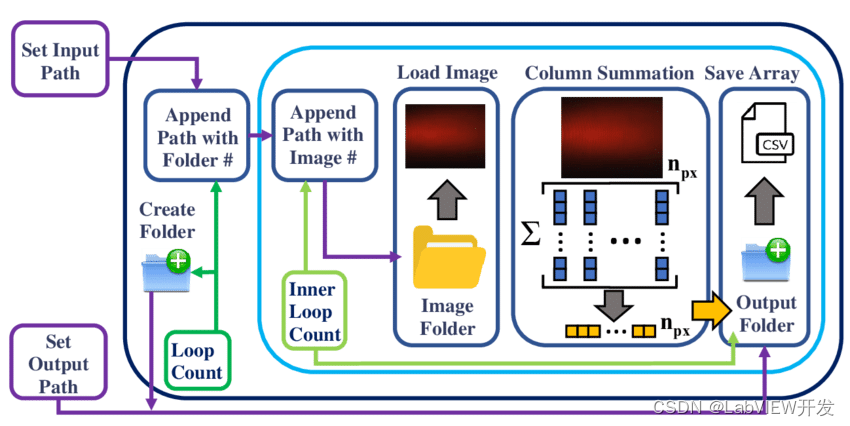
目前比较好用的LabVIEW架构及其选择
LabVIEW提供了多种架构供开发者选择,以满足不同类型项目的需求。选择合适的架构不仅可以提高开发效率,还能确保项目的稳定性和可维护性。本文将介绍几种常用的LabVIEW架构,并根据不同项目需求和个人习惯提供选择建议。 常用LabVIEW架构 1. …...

CSS之块浮动
在盒子模型的基础上就可以对网页进行设计 不知道盒子模型的可以看前面关于盒子模型的内容 而普通的网页设计具有一定的原始规律,这个原始规律就是文档流 文档流 标签在网页二维平面内默认的一种排序方式,块级标签不管怎么设置都会占一行,而同一行不能放置两个块级标签 行级…...
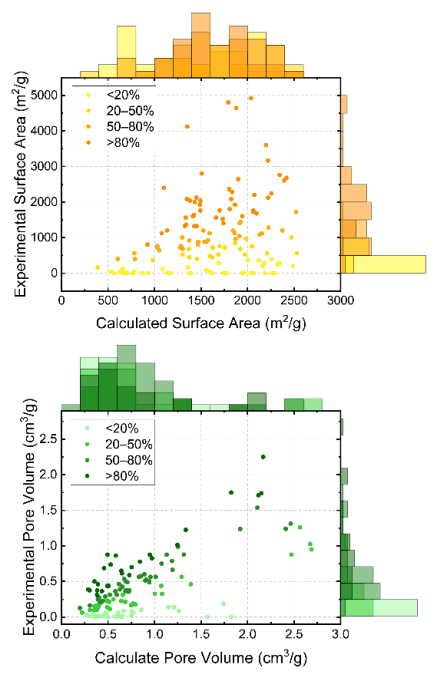
探索GPT-4V在学术领域的应用——无需编程即可阅读和理解科学论文
1. 概述 论文地址:https://arxiv.org/pdf/2312.05468.pdf 随着人工智能潜力的不断扩大,人工智能(AI)在化学领域的应用也在迅速发展。特别是大规模语言模型的出现,极大地扩展了人工智能在化学研究中的作用。由于这些模…...

耐用充电宝有哪些?优质充电宝到底选哪个?良心推荐!
在电量即生产力的现今时代,如何为移动设备寻找一位最佳的伴侣呢?一款耐用、优质的充电宝无疑是你的不二之选。今天我们将带您揭开市场隐藏的一面,揭示哪些充电宝品牌真正代表了耐用与品质的标杆。让我们一起深入了解并选购最适合自己的充电宝…...

何为屎山代码?
在编程界,有一种代码被称为"屎山代码"。这并非指某种编程语言或方法,而是对那些庞大而复杂的项目的一种形象称呼。屎山代码,也被称为"祖传代码",是历史遗留问题,是前人留给我们的"宝藏"…...

基于esp8266_点灯blinker_智能家居
文章目录 一 实现思路1 项目简介2 项目构成3 代码实现4 外壳部分 二 效果展示UI图片 一 实现思路 摘要:esp8266,mixly,点灯blinker,物联网,智能家居,3donecut 1 项目简介 1 项目效果 通过手机blinker app…...

Web前端开发交流群:深度探索、实践与创新的集结地
Web前端开发交流群:深度探索、实践与创新的集结地 在数字时代的浪潮中,Web前端开发扮演着举足轻重的角色。为了促进前端技术的交流与发展,Web前端开发交流群应运而生,成为众多开发者学习、分享、创新的集结地。本文将从四个方面、…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
