代码随想录算法训练营第三十八 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
我在每一个算法开始之前都会去认真的看一下这个理论基础,或者说是算法的主要思想,可以直接看视频carl讲解的很清晰;其次还会大致看一下这一part中的题型及难度
动态规划理论基础讲解链接:https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html视频:https://www.bilibili.com/video/BV13Q4y197Wg
509. 斐波那契数
https://programmercarl.com/0509.%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0.html
视频:https://www.bilibili.com/video/BV1f5411K7mo
class Solution {
public:int fib(int n) {if(n<=1) return n;//dp[i] 第i个斐波那契数值为dp[i]vector<int> dp(n+1);//初始化dp[0] = 0;dp[1] = 1;//遍历顺序:从前往后for(int i=2;i<=n;i++) {//递推公式dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};
70. 爬楼梯
https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频:https://www.bilibili.com/video/BV17h411h7UH
class Solution {
public:int climbStairs(int n) {//dp[i]表示 爬到第i层楼梯,有dp[i]种方法//上i-1层楼梯,有dp[i - 1]种方法,i层就加一//dp[i] = dp[i-1]+dp[i-2]if(n<=1) return n;//希望从i=1开始vector<int> dp(n+1); //犯了个低级错误定义成了dp[n+1]dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++) {dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};

746. 使用最小花费爬楼梯
https://programmercarl.com/0746.%E4%BD%BF%E7%94%A8%E6%9C%80%E5%B0%8F%E8%8A%B1%E8%B4%B9%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频讲解:https://www.bilibili.com/video/BV16G411c7yZ
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1);dp[0] = 0;dp[1] = 0;for(int i=2; i<=cost.size();i++) {dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};

相关文章:

代码随想录算法训练营第三十八 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
我在每一个算法开始之前都会去认真的看一下这个理论基础,或者说是算法的主要思想,可以直接看视频carl讲解的很清晰;其次还会大致看一下这一part中的题型及难度 动态规划理论基础讲解链接:https://programmercarl.com/%E5%8A%A8%E6…...

如何有效处理服务器后台密码暴露
服务器后台密码的暴露是信息安全领域中的严重事件,它可能引发未经授权的数据访问、恶意软件植入或系统功能滥用等一系列问题。本文将探讨几种处理服务器后台密码暴露的有效策略,包括紧急响应步骤、密码安全增强措施及长期预防机制,并提供实际…...

使用本地大模型调用代码,根本就是一场骗局!
通过大模型调用其他工具到底可不可行?ChatGPT 或许能轻松搞定一切,但同样的需求落在本地大模型上,恐怕就要打个问号了。 法国开发工程师 Emilien Lancelot 尝试了多款号称具备工具调用功能的 agent 框架,来看看本地大模型到底能不…...

一些简单却精妙的算法
文章目录 1.树状数组2.红黑树3.星星打分4.欧几里得算法5.快速幂6.并查集 在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。 1.树状数组 int lowbit(int x) { …...

git多账号使用报错:You don‘t have permissions to push to “xxx/xxxx“ onGitHub. Would
git多账号使用报错:You don’t have permissions to push to “xxx/xxxx” onGitHub. Would 有的时候我们有两个甚至多个git账号(公司的git账号和自己的github),为了不混淆提交,我们需要在提交之前查看自己的git账号必…...
2023年12月真题C语言软件编程等级考试三级(含详细解析答案))
中国电子学会(CEIT)2023年12月真题C语言软件编程等级考试三级(含详细解析答案)
中国电子学会(CEIT)考评中心历届真题(含解析答案) C语言软件编程等级考试三级 2023年12月 编程题五道 总分:100分一、因子问题(20分) 任给两个正整数N、M,求一个最小的正整数a,使得a和(M-a)都是N的因子。 时间限制: 10000ms 内存限制: 65536kb 输入 包括两个整…...

多线程爬取百度图片
爬取网页图片 import urllib.parse import requests import os import time from concurrent.futures import ThreadPoolExecutorheaders {"User-Agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/125.0.0.0…...

RK3568-修改fiq-debugger调试串口
瑞芯微SDK默认将uart2_m0作为调试串口,以下方法将调试串口修改为uart5_m1。修改bootloader 修改/OK3568-linux-source/rkbin/tools/ddrbin_param.txt文件,5表示串口5。1表示复用m1。执行./ddrbin_tool ddrbin_param.txt ../bin/rk35/rk3568_ddr_1560MHz_v1.11.bin命令修改ub…...

我们离成功有多远呢?只要能完成自己阶段性的目标就算是一次成功
做起一个账号,带好一个团队,经营好一家公司,似乎这些都能叫成功,成功的定义可大可小,而我认为只要能完成自己阶段性的目标就算是一次成功,毕竟每个人学历、背景、阅历、资源、认知都不同,很难同…...

Golang 避坑指南
文章目录 1. Channel 与 Goroutine 泄露1.1 发送不接收1.2 接收不发送1.3 nil channel2. 跳出 for-switch 或 for-select 3.for 迭代变量3.1 闭包中的for迭代变量3.2 for range 迭代变量 4. 循环内的 defer5.defer 函数的参数值6.nil interface 和 nil interface 值7.结构体指针…...
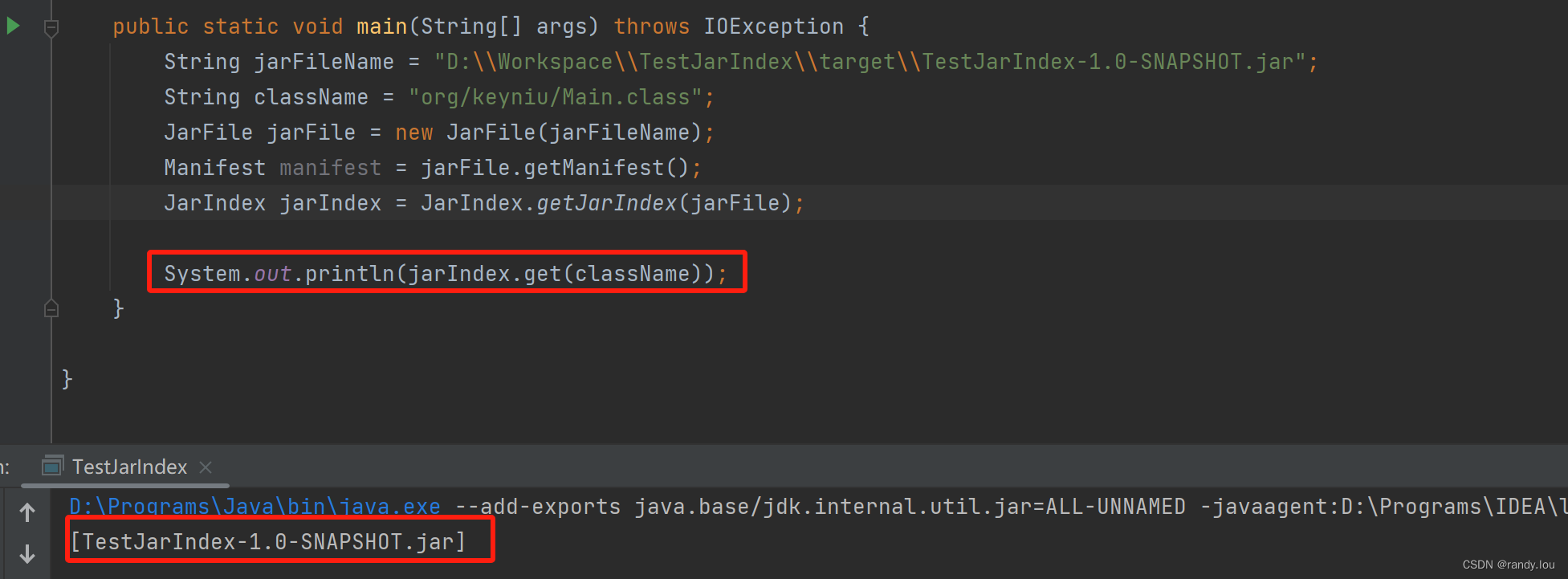
Java核心: JarIndex的使用
在讲解Java类加载器的时候,我们发现URLClassLoader加载类或资源时通过访问ClassPath下的每一个路径,来确定类是否存在的,假设我们执行的命令是这样的 java -classpath D:\DiveInSpring\target\classes;C:\lib\spring-expression.jar;C:\lib\…...

1052 卖个萌(测试点1,2)
solution 想要输出\需要用\\才能输出,即 cout << "Are you kidding me? \\/" << endl;测试点1,2:输入序号小于1的非法情况 #include<iostream> #include<string> #include<map> using namespace…...

Vue 3与ESLint、Prettier:构建规范化的前端开发环境
title: Vue 3与ESLint、Prettier:构建规范化的前端开发环境 date: 2024/6/11 updated: 2024/6/11 publisher: cmdragon excerpt: 这篇文章介绍了如何在Vue 3项目中配置ESLint和Prettier以统一代码风格,实现代码规范性与可读性的提升。通过设置规则、解…...

npm安装依赖过慢
今天在使用npm安装taro框架的依赖时,速度慢到吐血,使用了淘宝镜像源依然很慢,安装一个多小时没反应,最后清理了缓存再次安装速度就快很多了,因此解决方法大致有两种: 使用淘宝镜像源 原域名: ht…...

计算机毕业设计 | SpringBoot+vue的教务管理系统
1,绪论 1.1 项目背景 在这个资讯高度发展的时代,资讯管理变革已经是一个更为宽泛、更为全面的潮流。为了保证中国的可持续发展,随着信息化技术的不断进步,教务管理体系也在不断完善。与此同时,伴随着信息化的飞速发展…...

深入探索深度学习的验证集:必要还是可选?
深入探索深度学习的验证集:必要还是可选? 在深度学习项目的设计和实施过程中,数据通常被划分为训练集、测试集,以及有时的验证集。尽管在一些研究中,我们可能看到只有训练集和测试集被使用,验证集的作用及…...

初识C++ · 反向迭代器简介
目录 前言 反向迭代器的实现 前言 继模拟实现了list和vector之后,我们对迭代器的印象也是加深了许多,但是我们实现的都是正向迭代器,还没有实现反向迭代器,那么为什么迟迟不实现呢?因为难吗?实际上还好。…...

fastapi学习前置知识点
前置知识点 FastApi:一个用于构建API的现代、快速(高性能)的web框架。 FastApi是建立在Pydantic和Starlette基础上,Pydantic是一个基于Python类型提示来定义数据验证、序列化和文档的库。Starlette是一种轻量级的ASGI框架/工具包…...

机器学习常见知识点 1:Baggin集成学习技术和随机森林
文章目录 1、集成学习a.BaggingBagging的工作原理1. 自助采样(Bootstrap Sampling)2. 训练多个基学习器3. 聚合预测 Bagging的优点Bagging的缺点应用场景 b.Boosting 2、决策树3、随机森林随机森林的核心概念1. 集成学习2. 决策树 构建随机森林的步骤1. …...

容器(Docker)安装
centos安装Docker sudo yum remove docker* sudo yum install -y yum-utils#配置docker的yum地址 sudo yum-config-manager \ --add-repo \ http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo#安装指定版本 - 可以根据实际安装版本 sudo yum install -y docke…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
