【数据结构】带你深入理解栈

一. 栈的基本概念💫
栈是一种特殊的线性表。其只允许在固定的一端进行插入和删除元素的操作,进行数据的插入和删除的一端称作栈顶,另外一端称作栈底。栈不支持随机访问,栈的数据元素遵循后进先出的原则,即LIFO(Late In First Out)。
也许有人曾经听说过压栈和入栈的术语,以下是它们的定义:
压栈:栈的插入操作叫做进栈/压栈/入栈,插入数据是在栈顶
出栈:栈的删除操作叫做出栈/弹栈,删除数据也是在栈顶
我们结合动图来理解栈的后进先出:

二. 栈实现方法的分析与选择👉
2.1 引入
我们可以使用顺序存储结构或者链式存储结构来实现栈。换句话来说,我们可以使用之前学习过的顺序表或者链表来实现栈,它们各自有自己的优缺点,下面我们就来分析分析。
2.2 用顺序表来实现
以下是动态顺序表实现栈的结构体声明和图示:
typedef struct StackList
{STDataType* a; //指向动态开辟的空间int top; //栈顶所在下标,相当于元素个数int capacity;//顺序表容量
}ST;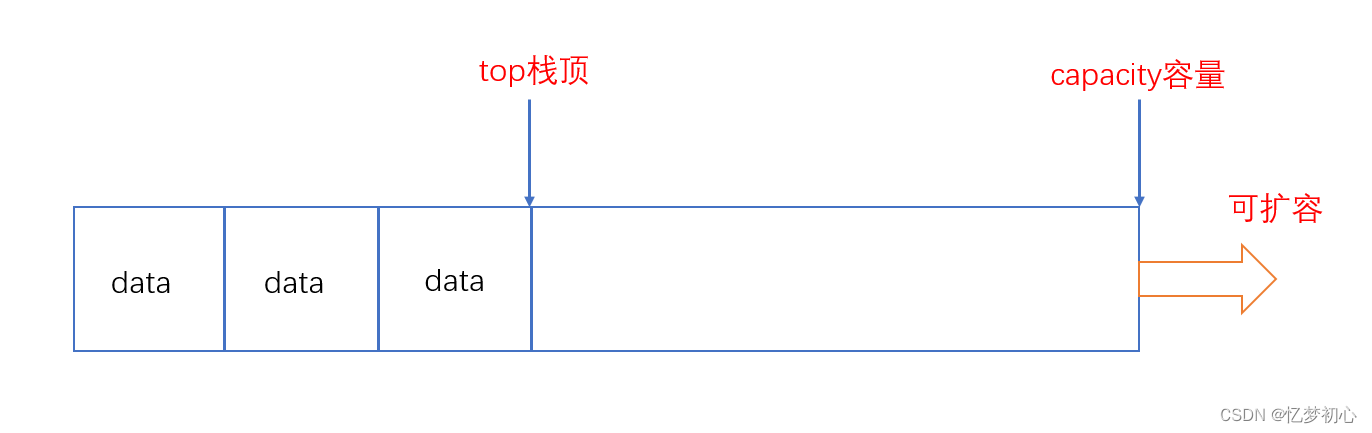
优点:由于栈的插入和删除数据符合后进先出的原则,我们把顺序表末端当作栈顶,则插入数据和删除数据就是尾插和尾删。而前面我们知道顺序表的尾插和尾删效率非常高,时间复杂度为O(1)。
缺点:存在容量限制,当容量不足是需要扩容,扩容需要成本。
2.3 用链表来实现
2.3.1 单链表实现(尾为栈顶)
typedef struct StackNode
{STDataType x;//数据域StackNode* nest;//指针域,指向下一结点
}ST;
struct Stack
{ST* phead;//指向第一个结点ST* tail;//指向尾结点
}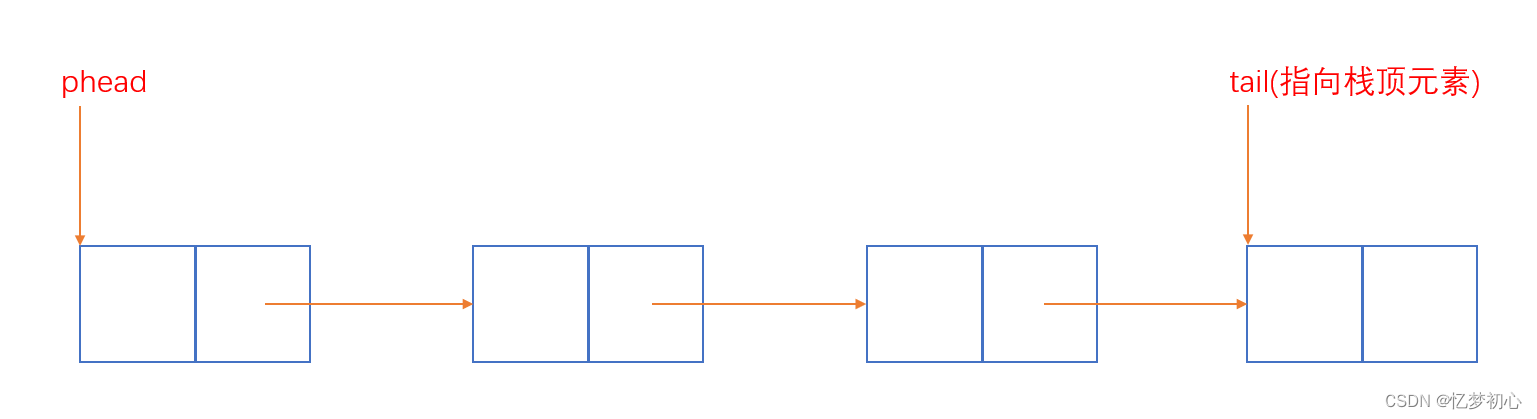
假如我们使用链表尾当作栈顶,则对应的插入删除就是尾插和尾删。我们知道单链表的尾插和尾删要先找到链表尾,时间复杂度是O(N)。可能有人会想,那我定义一个尾指针来记录链表尾部,想法很好,但是这样虽然解决了尾插效率低的问题,但是尾删除了要找到最后一个结点,还要找到其前面的结点,由于链表单向,最终还是要遍历链表,没有什么意义。
2.3.2 单链表实现(头为栈顶)
我们知道,和顺序表相反,单链表头插和头删效率较高,时间复杂度为O(1)。我们就可以将链表头当作栈顶,这样插入就相当于头插,删除就相当于头删,如下:
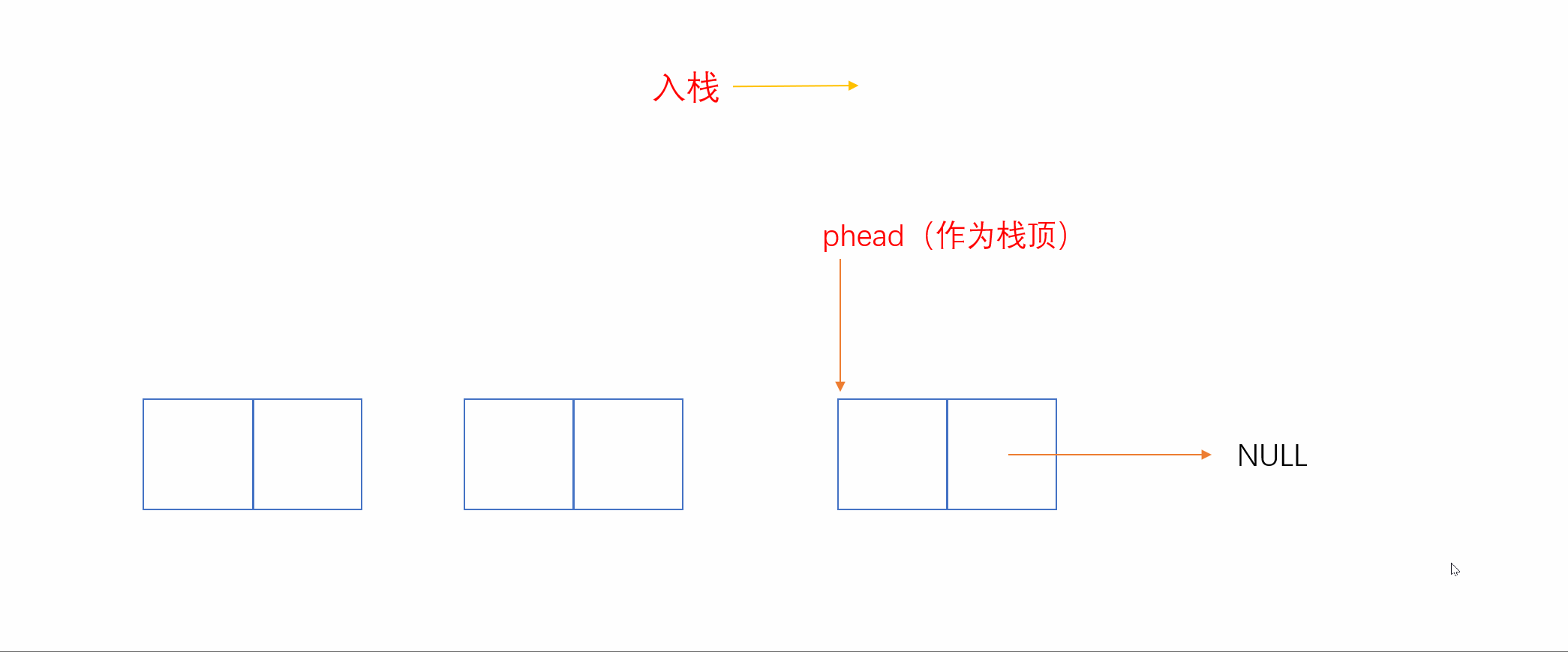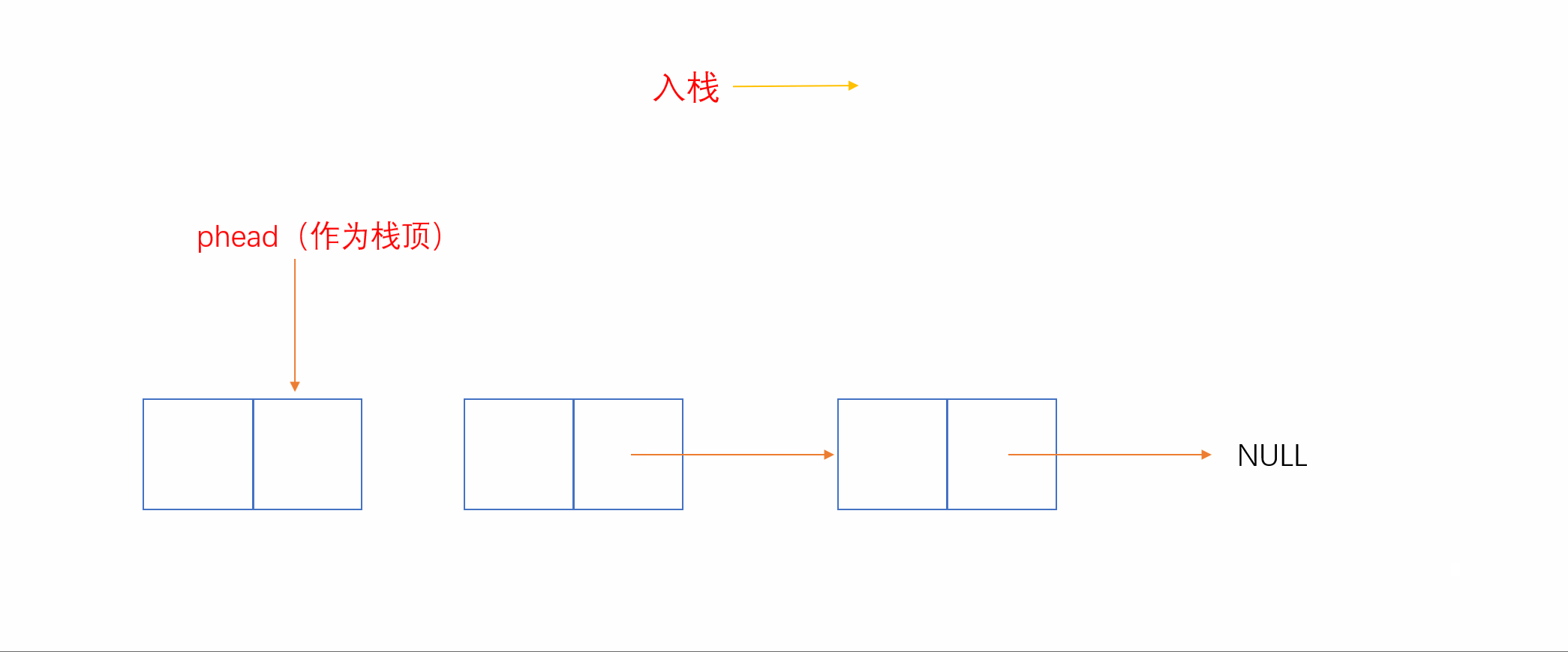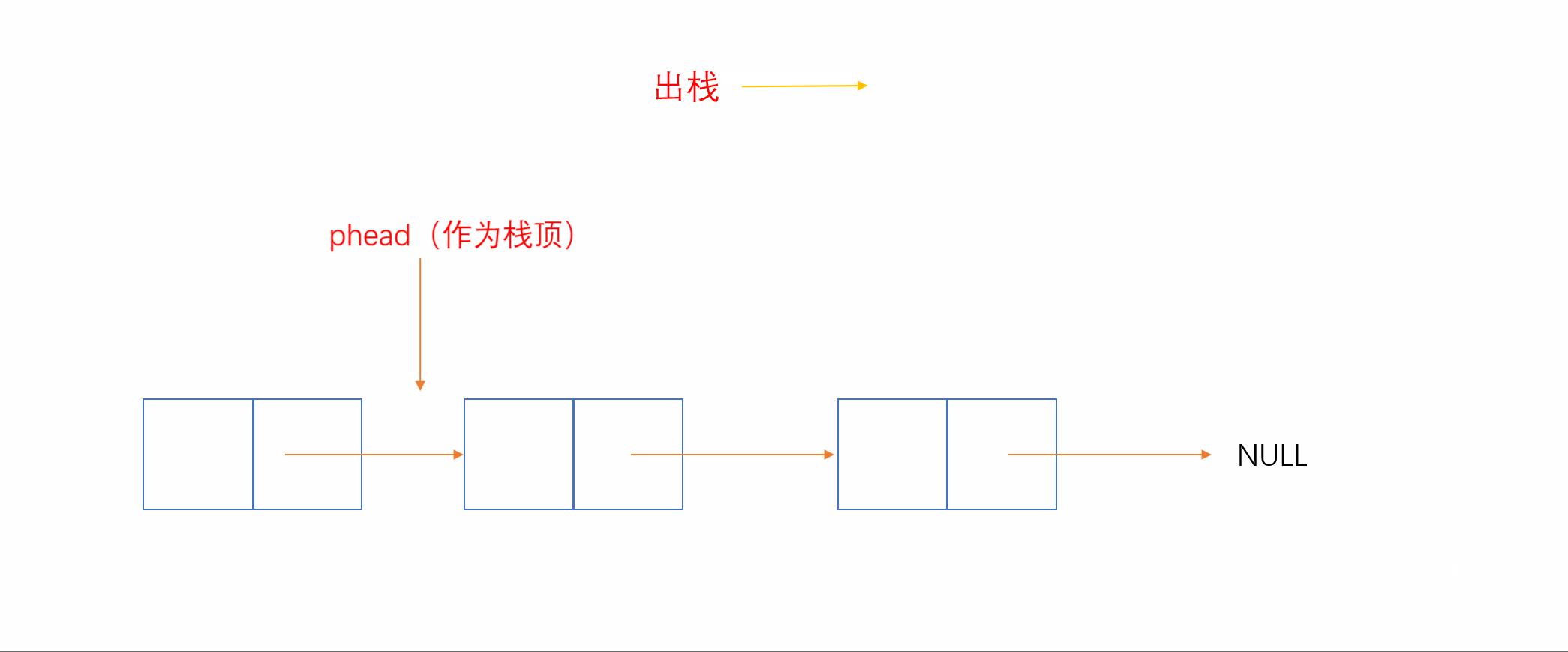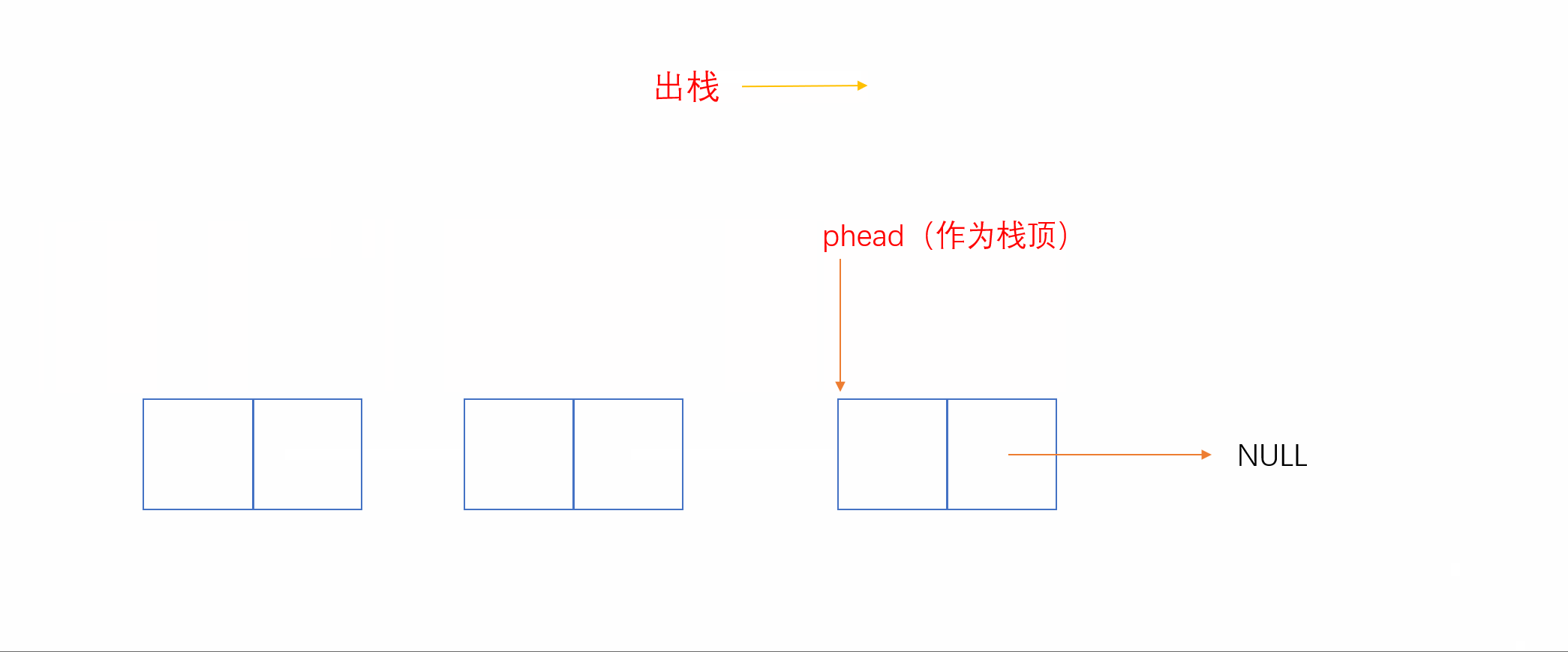
2.3.3 双向链表实现
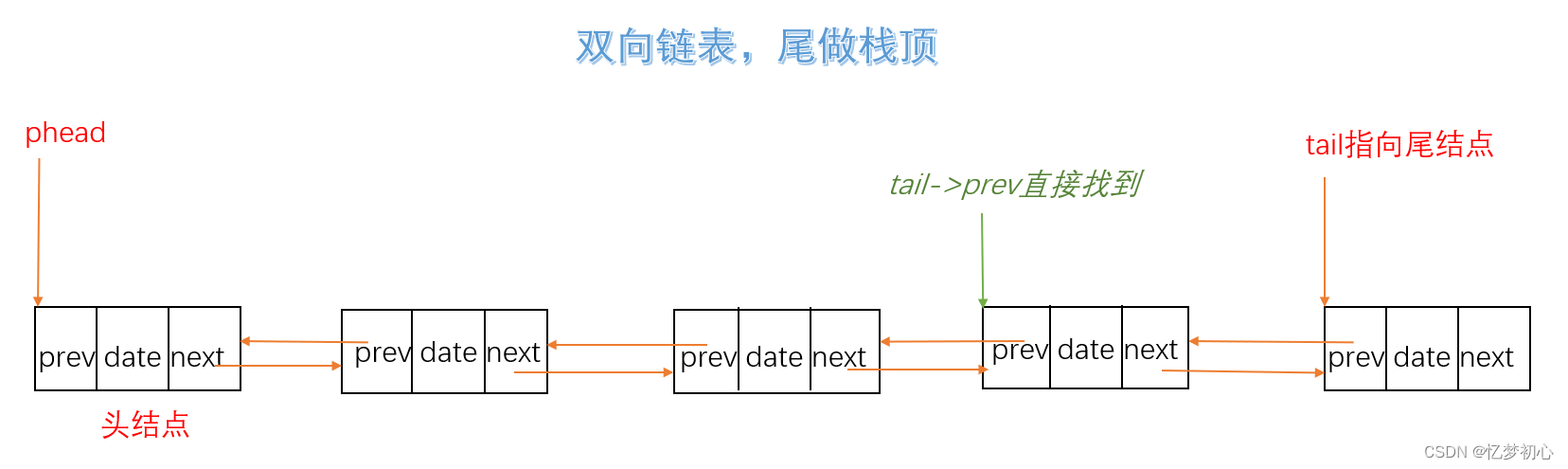
如果一定要使用链表以及把链表尾当作栈顶,为了解决删除需要找到尾结点的前驱结点时间效率低的问题,我们可以用双向链表来实现栈。双向链表除了后继指针还增加了前驱指针来指向上一个结点,利用这个结构可以直接得到上一个结点,无需再遍历链表,时间复杂度为O(1)。
typedef struct StackNode
{STDataType x;//数据域StackNode* nest;//后继指针域,指向下一结点StackNode* prev;//前驱指针域,指向上一结点
}ST;
struct Stack
{ST* phead;//指向第一个结点ST* tail;//指向尾结点
}
2.3.4 总结
如果没有要求栈顶的位置,则我们还是使用单链表来实现,将头作为栈顶。这是因为双向链表比单链表的结点多占用了一个前驱指针的空间,虽然现代计算机空间已然构不成太大问题,但是能省则省,大伙们懂的😏。
如果题目要求栈顶在链表尾的话,那还是老老实实用双向链表实现吧。
使用链表的缺点就是每次插入都要malloc新结点,会消耗一定的时间成本。
2.4 选择
我们推荐采用顺序表来实现对栈的操作,原因如下:
1. 栈的特性完美避开了顺序表尾插尾删效率过低的问题,虽然需要扩容,但是链表创建结点也同样需要成本,而顺序表扩容频率不像链表一样如此频繁。
2. 我们知道CPU与主存速度上存在巨大差距,为了提高效率,CPU和主存之间还存在着cache高速缓存。CPU访问cache的速度是快于主存的。每次CPU取数据时会访问cache看看存不存在所需的数据,如果不存在才会访问主存,然后将数据所在的内存块加载到cache中。由于顺序表空间是连续的,根据cache的空间局部性原理,采用顺序表cache的命中率会高于链表,效率高。
三. 接口的实现✈
3.1 栈的声明
本文我们采用动态顺序表来实现栈,结构体的声明如下:
typedef int STDataType;
typedef struct StackList
{STDataType* a;//指向动态开辟的空间int top; //栈顶所在下标,相当于元素个数int capacity;//栈的容量
}ST;和前面链表顺序表一样,我们不直接指定数据的类型,而是将类型重定义为STDataType,这样做有利于提高代码的可维护性。
3.2 初始化和销毁
和其他数据结构一样,当我们使用栈结构之前需要对其进行初始化,当我们不再使用它是要对它进行销毁,具体代码如下:
//初始化栈
void StackInit(ST* ps) //需要改变实参,传指针
{assert(ps);//确保传入的指针不为空ps->a = (STDataType*)malloc(4 * sizeof(STDataType));//起初先分配四个字节空间ps->capacity = 4;ps->top = 0;
}//销毁栈
void StackDestroy(ST* ps)
{assert(ps);free(ps->a);//将栈空间释放掉//将栈结构中的信息清空ps->capacity = 0;ps->top = 0;ps->a = NULL;
}3.3 入栈
由于栈只允许在固定的一端插入,我们又将末端当作栈顶,因此入栈就是尾插。而顺序表的尾插我们已经很清楚了,往栈顶所在下标放入数据,然后栈顶下标加1即可。效果和代码如下:

//入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity) //元素个数等于容量,栈满了,先扩容{STDataType* temp = (STDataType*)realloc(ps->a, 2 * ps->capacity*sizeof(STDataType));if (temp == NULL)//失败则退出程序{printf("扩容失败\n");exit(-1);}else{ps->a = temp;ps->capacity *= 2;temp = NULL;}}(ps->a)[ps->top] = x;//入栈(ps->top)++;//更新栈顶位置
}3.4 出栈
和入栈一样,出栈也只在固定的一端进行。入栈是尾插,则出栈就是尾删。而我们用顺序表来实现栈,因此尾删只需要将栈顶退后一位即可。
这里有人可能会将栈顶的元素置0然后再将栈顶位置后退一位。实际上这种方法并不可取,有以下两种原因:
1. 如果栈顶的元素本身就是0,那我们的行为就失去了意义。
2. 栈的元素类型不一定是整形,如果是浮点型或者结构体,我们赋值为0显然是不妥的。
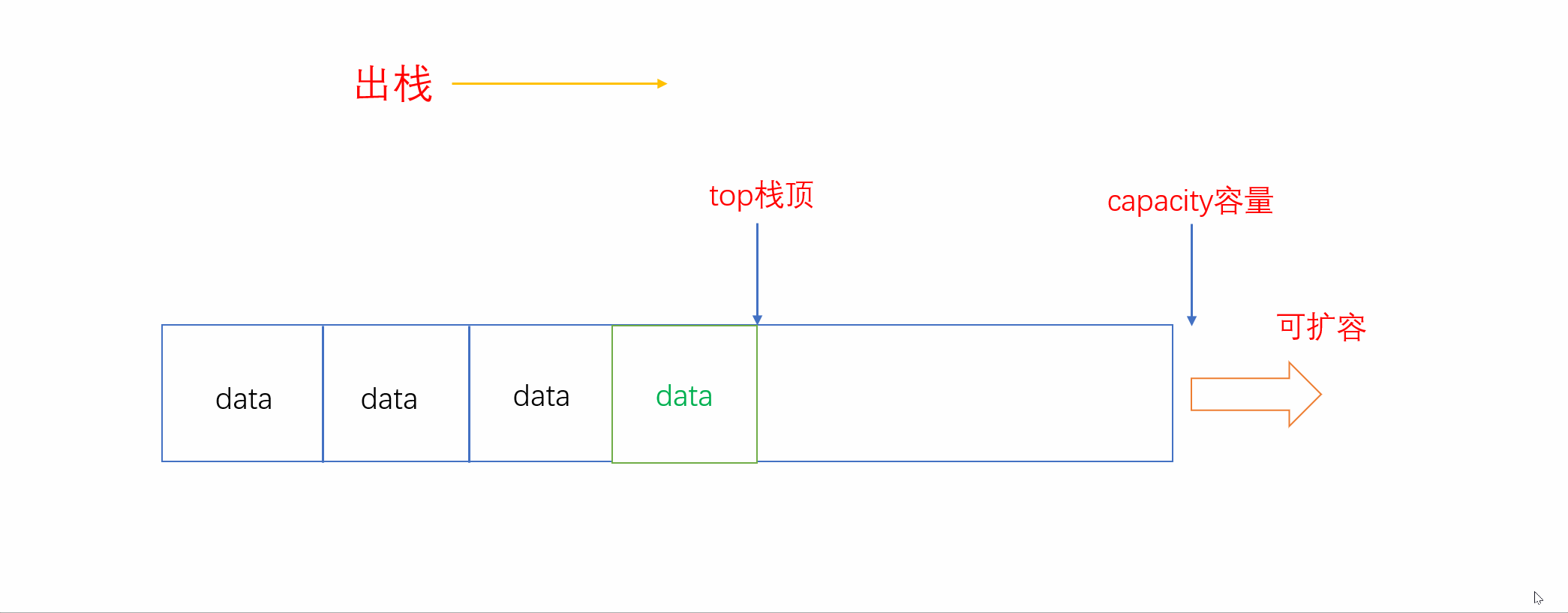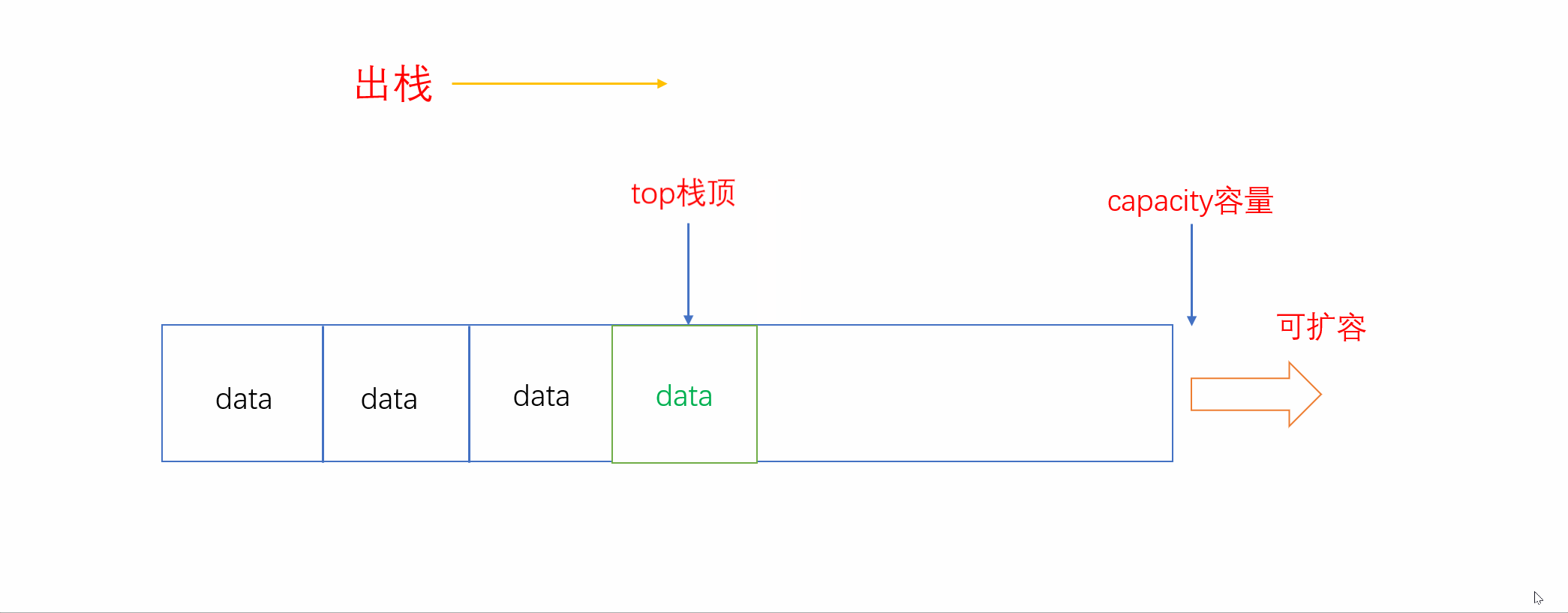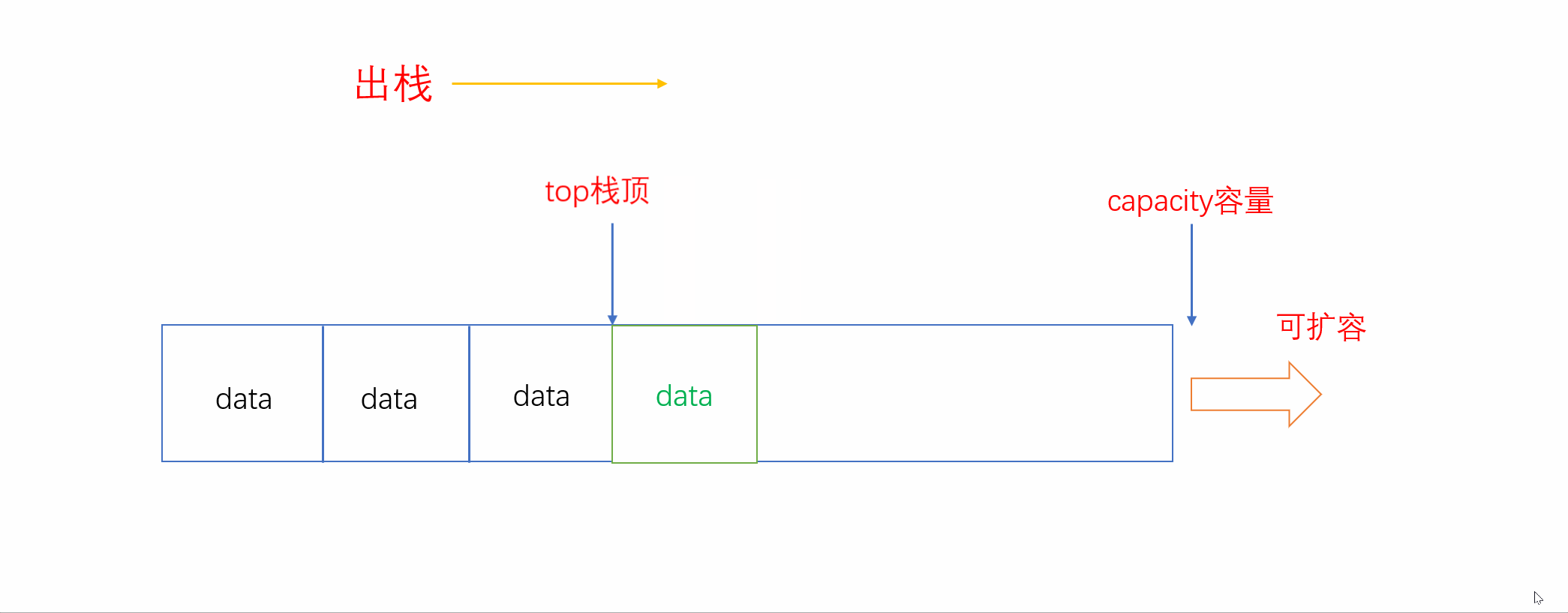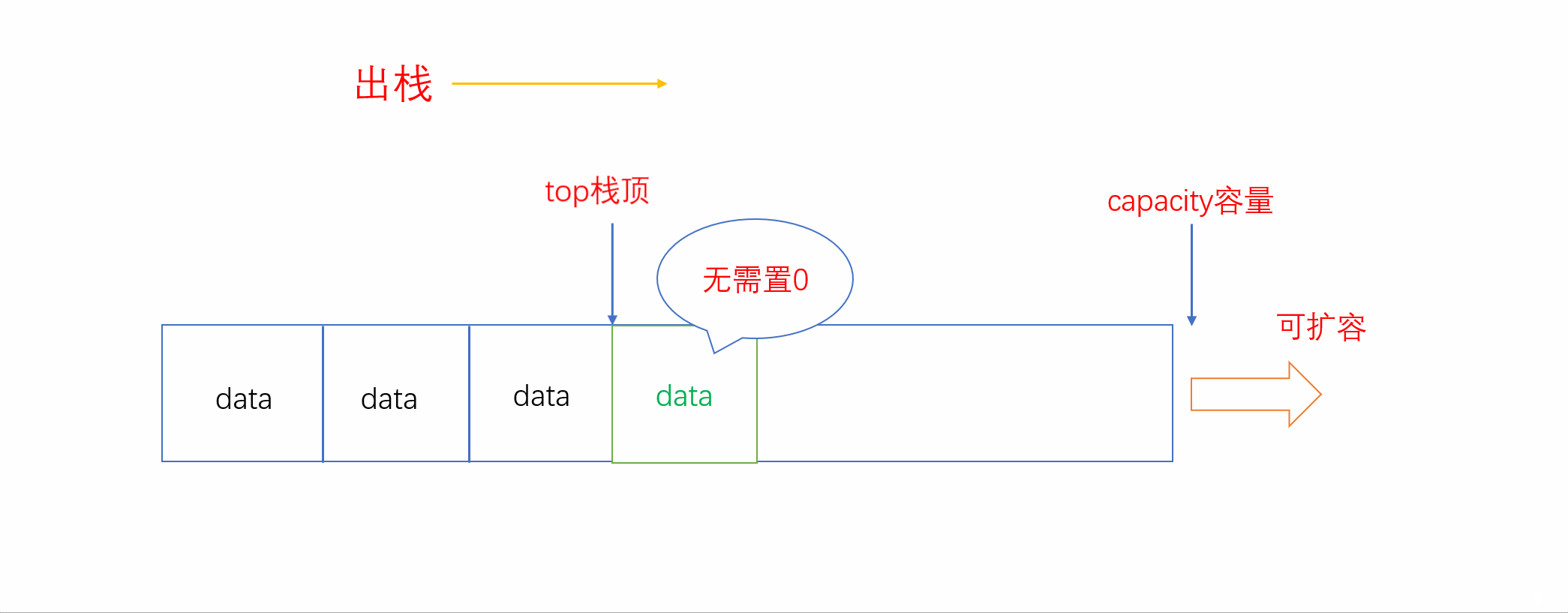
//出栈
void StackPop(ST* ps)
{assert(ps);//确保传入指针不为空assert(ps->top);//确保栈存在元素(ps->top)--;//更新栈顶
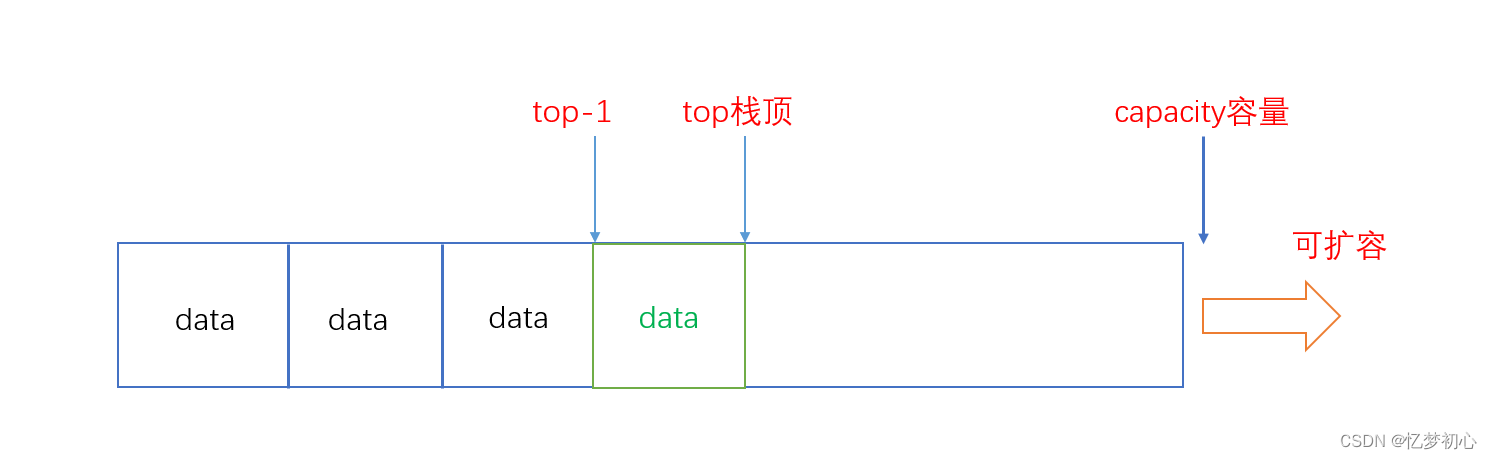
}3.5 求栈顶元素
很简单,我们可以直接根据栈顶所在的下标得到栈顶元素,如下:
//求栈顶元素
STDataType StackTop(ST* ps)
{assert(ps);assert(ps->top);//确保栈中存在元素return ps->a[ps->top - 1];//栈顶元素所在下标即为top-1
}3.6 判空
在我们设计的栈结构中,top实际上就等价于元素个数,通过判断top是否为0就可以知道栈是否为空。我们使用了C语言stdbool.h头文件中的bool类型,其只能用来存放true(1)和false(0)两个值,分别代表真和假。代码如下:
//判空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top;//top为0则返回false,不为零返回true
}3.7 求栈的元素个数
根据我们构造的栈结构体,栈顶top的值就是栈的元素个数,直接返回即可:
//求栈的元素个数
int StackSize(ST* ps)
{assert(ps);return ps->top;
}3.8 思考
会不会有人会有以下思考:
1. 求栈顶元素,判空,求元素个数都是用一行直接返回,这些接口会不会有些许多余,直接访问结构体相应成员不就好了?
2. 为什么没有实现查找,打印,修改等接口?
下面我们来分析一下:
我们要知道,数据结构的实现方式多种多样,在本文我们将栈元素个数作为栈顶的下标,那可不可以将最后一个元素的下标作为栈顶下标呢?实际上完全可以。那么就会出现一个问题,如果我们使用别人已经封装好的栈,我们要怎么知道栈顶元素下标是top还是top-1呢?我们要怎么知道是top=0为空还是top=-1为空呢?我们要怎么知道元素个数是top还是top+1呢?我们完全不知道,只有设计者才知道,因此设计者往往会将这些功能再封装成函数,供我们直接调用。
这是因为栈是一种限制型数据结构,其不支持随机访问,只允许在固定的一端(栈顶)进行插入和删除操作,不允许在其他的位置进行任何操作。因此,栈不存在查找,打印,修改等对除栈顶之外的位置进行操作的接口,否则会破坏栈的特性。为了遵循栈的特性,我们就不实现这些接口。
四. 完整代码及效果展示🌠
按照以往惯例,我们采用多文件编写的形式,将上述接口的定义实现放在Stack.c文件中,然后将接口的声明和结构体的定义放于Stack.h头文件中,以达到封装的效果。这样我们如果需要使用栈,就只需要在文件中包含对应的头文件Stack.h就可以使用我们上面定义的各种接口。以下为本文实现的栈完整代码以及效果展示:
//Stack.h文件,用于声明接口函数,定义结构体
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;
typedef struct StackList
{STDataType* a;//指向动态开辟的空间int top; //栈顶所在下标,相当于元素个数int capacity;//栈的容量
}ST;//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);
//出栈
void StackPop(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//求栈顶元素
STDataType StackTop(ST* ps);
//求栈元素个数
int StackSize(ST* ps);
//判空
bool StackEmpty(ST* ps);//Stack.c文件,用于定义接口函数
#include"Stack.h"//初始化栈
void StackInit(ST* ps) //需要改变实参,传指针
{assert(ps);//确保传入的指针不为空ps->a = (STDataType*)malloc(4 * sizeof(STDataType));//起初先分配四个字节空间ps->capacity = 4;ps->top = 0;
}//入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity) //元素个数等于容量,栈满了,先扩容{STDataType* temp = (STDataType*)realloc(ps->a, 2 * ps->capacity * sizeof(STDataType));if (temp == NULL)//失败则退出程序{printf("扩容失败\n");exit(-1);}else{ps->a = temp;ps->capacity *= 2;temp = NULL;}}(ps->a)[ps->top] = x;//入栈(ps->top)++;//更新栈顶位置
}//出栈
void StackPop(ST* ps)
{assert(ps);//确保传入指针不为空assert(ps->top);//确保栈存在元素(ps->top)--;//更新栈顶
}//求栈顶元素
STDataType StackTop(ST* ps)
{assert(ps);assert(ps->top);//确保栈中存在元素return ps->a[ps->top - 1];//栈顶元素所在下标即为top-1
}//求栈的元素个数
int StackSize(ST* ps)
{assert(ps);return ps->top;
}//判空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top;//top为0则返回false,不为零返回true
}//销毁栈
void StackDestroy(ST* ps)
{assert(ps);free(ps->a);//将栈空间释放掉//将栈结构中的信息清空ps->capacity = 0;ps->top = 0;ps->a = NULL;
}最后, 我们在tesst.c文件调用栈各个接口进行测试,如下:
//test.c文件,用于测试
#include"Stack.h"void test01()
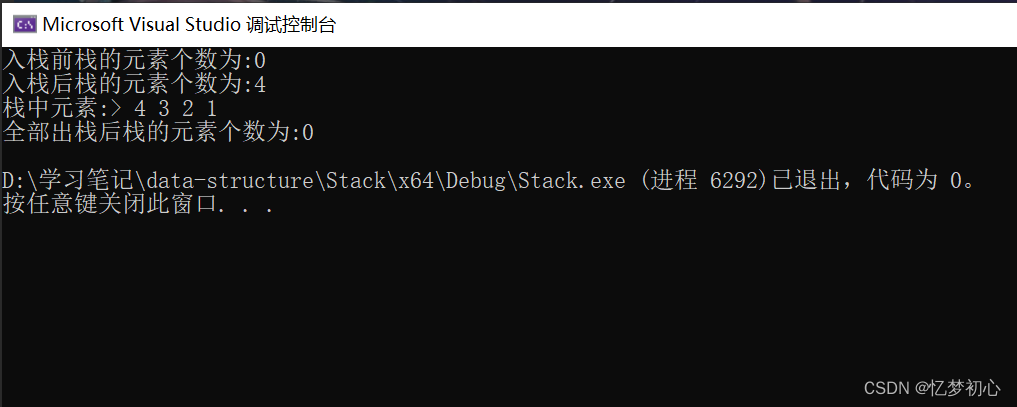
{ST s1;//初始化StackInit(&s1);//求元素个数printf("入栈前栈的元素个数为:%d\n", StackSize(&s1));//入栈StackPush(&s1,1);StackPush(&s1, 2);StackPush(&s1, 3);StackPush(&s1, 4);printf("入栈后栈的元素个数为:%d\n", StackSize(&s1));//由于无法遍历打印,我们就交替使用 求栈顶元素-出栈 来显示栈中元素printf("栈中元素:> ");while (StackEmpty(&s1))//栈不为空则继续{//求栈顶元素printf("%d ", StackTop(&s1));//出栈StackPop(&s1);}//全部出栈printf("\n全部出栈后栈的元素个数为:%d\n", StackSize(&s1));//销毁StackDestroy(&s1);
}int main()
{test01();return 0;
}以下是测试的最终效果:
以上,就是本期的全部内容啦🌸
制作不易,能否点个赞再走呢🙏
相关文章:

【数据结构】带你深入理解栈
一. 栈的基本概念💫栈是一种特殊的线性表。其只允许在固定的一端进行插入和删除元素的操作,进行数据的插入和删除的一端称作栈顶,另外一端称作栈底。栈不支持随机访问,栈的数据元素遵循后进先出的原则,即LIFOÿ…...
认识CSS之如何提高写前端代码的效率
🌟所属专栏:前端只因变凤凰之路🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该系列将持续更新前端的相关学习笔记,欢迎和我一样的小白订阅,一起学习共同进步~👉文章简…...

Vue中watch和computed
首先这里进行声明,这个讲的是vue2的内容,在vue3发生了什么变动与此无关 这里是官网: https://v2.cn.vuejs.org/v2/guide/installation.html computed > 计算属性 watch > 侦听器(也叫监视器) 其区别如下&…...

华为鲲鹏+银河麒麟v10 安装 docker-ce
设备:硬件:仅有ARM处理器,无GPU和NPU,操作系统麒麟银河V10,Kunpeng-920 #######参考原链接######### 华为鲲鹏银河麒麟v10 安装 docker-ce 踩坑 - akiyaの博客 在 arm64(aarch64) 架构服务器上基于国产化操作系统安…...

Lambda,Stream,响应式编程从入门到放弃
Lambda表达式 Java8新引入的语法糖 Lambda表达式*(关于lambda表达式是否属于语法糖存在很多争议,有人说他并不是语法糖,这里我们不纠结于字面表述)*。Lambda表达式是一种用于取代匿名类,把函数行为表述为函数式编程风…...

C语言枚举使用技巧
什么是C语言枚举 C语言枚举是一种用户自定义数据类型,它允许程序员定义一个变量,并将其限制为一组预定义的常量。这些常量被称为“枚举值”,并且可以通过名称进行引用。 在C语言中,枚举值是整数类型,它们的值默认从0…...

保姆级使用PyTorch训练与评估自己的EfficientNetV2网络教程
文章目录前言0. 环境搭建&快速开始1. 数据集制作1.1 标签文件制作1.2 数据集划分1.3 数据集信息文件制作2. 修改参数文件3. 训练4. 评估5. 其他教程前言 项目地址:https://github.com/Fafa-DL/Awesome-Backbones 操作教程:https://www.bilibili.co…...

【9】基础语法篇 - VL9 使用子模块实现三输入数的大小比较
VL9 使用子模块实现三输入数的大小比较 【报错】官方平台得背锅 官方平台是真的会搞事情,总是出一些平台上的莫名其妙的错误。 当然如果官方平台是故意考察我们的细心程度,那就当我没有说!! 在这个程序里,仿真时一直在报错 错误:无法在“test”中绑定wire/reg/memory“t…...

成功的项目管理策略:减少成本,提高质量
项目管理是一项具有挑战性的任务,项目团队需要合理的规划和策略,以确保项目的成功和达成预期。为了实现项目的成功,项目经理必须采用正确的策略,才能以最大限度地减少成本并提高项目质量。本文将探讨成功的项目管理策略࿰…...

centos 7下JDK8安装
下载安装包https://www.oracle.com/java/technologies/downloads/#java8-linux上传路径 /usr/local(替换为自己需要安装的路径)解压tar -zxvf jdk-8u131-linux-x64.tar.gz配置环境变量[rootlocalhost java]# vi /etc/profile添加如下配置在配置文件最后&…...

datatables.js中文项目使用案例
官方下载地址https://datatables.net/download/中文官网:http://datatables.club/资源引用<link href"~/datatables/datatables.min.css" rel"stylesheet" /> <script src"~/jquery.min.js" type"text/javascript"…...

Hadoop小结
Hadoop是什么Hadoop是一 个由Apache基金 会所开发的分布式系统基础架构。主要解决,海量数据的存储和海量数据的分析计算问题。广义上来说,Hadoop通 常是指一个更广泛的概念一Hadoop 生态圈。Hadoop优势Hadoop组成HDFS架构Hadoop Distributed File System,…...
)
经典卷积模型回顾14—vgg16实现图像分类(tensorflow)
VGG16是由牛津大学计算机视觉小组(Visual Geometry Group)开发的深度卷积神经网络模型。其结构由16层组成,其中13层是卷积层,3层是全连接层。 VGG16被广泛应用于各种计算机视觉任务,如图像分类、目标检测和人脸识别等。…...

#Vue2篇:keep-alive的属性和方法
定义 keep-alive 组件是 Vue.js 内置的一个高阶组件,用于缓存其子组件,以提高组件的性能和响应速度。 除了基本用法之外,它还提供了一些属性和方法,以便更好地控制缓存的组件。 属性 include属性用于指定哪些组件应该被缓存&a…...
webpack指南(项目篇)——webpack在项目中的运用
系列文章目录 webpack指南(基础篇)——手把手教你配置webpack webpack指南(优化篇)——webpack项目优化 文章目录系列文章目录前言一、配置拆分二、修改启动命令三、定义环境变量四、配置路径别名总结前言 前面我们对webpack的基…...
unicode字符集与utf-8编码的区别,unicode转中文工具、中文转unicode工具(汉字)
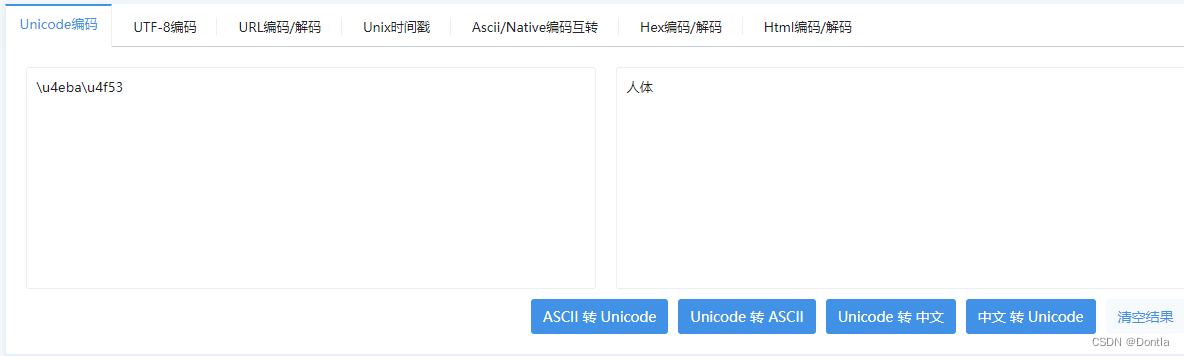
在cw上报的报警信息中,有一个name字段的值是\u4eba\u4f53 不知道是啥,查了一下,是unicode编码,用下面工具转换成汉字就是“人体” 参考文章:https://tool.chinaz.com/tools/unicode.aspx 那么我很好奇,uni…...

3D数学系列之——再谈特卡洛积分和重要性采样
目录一、前篇文章回顾二、积分的黎曼和形式三、积分的概率形式(蒙特卡洛积分)四、误差五、蒙特卡洛积分计算与收敛速度六、重要性采样七、重要性采样方法和过程八、重要性采样的优缺点一、前篇文章回顾 在前一篇文章3D数学系列之——从“蒙的挺准”到“蒙…...

Python错误 TypeError: ‘NoneType‘ object is not subscriptable解决方案汇总
目录前言一、引发错误来源二、解决方案2-1、解决方案一(检查变量)2-2、解决方案二(使用 [] 而不是 None)2-3、解决方案三(设置默认值)2-4、解决方案四(使用异常处理)2-5、解决方案五…...

VMware空间不足又无法删除快照的解决办法
如果因为快照删除半路取消或者失败,快照管理器就不再显示这个快照,但是其占用的空间还在,最终导致硬盘不足。 可以百度到解决方案,就是在快照管理器,先新建一个,再点删除,等待删除完成就可以将…...
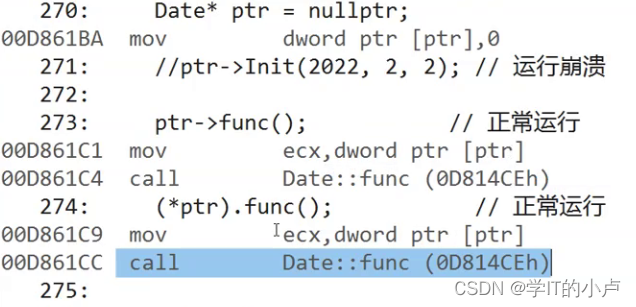
类和对象(一)
类和对象(一) C并不是纯面向对象语言 C是面向过程和面向对象语言的! 面向过程和面向对象初步认识: C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。 C是基…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
