当前位置：首页 > news >正文

mac 安装HomeBrew

news 2026/5/13 1:35:41

一、HomeBrew是什么？

homebrew是一款Mac OS平台下的软件包管理工具，拥有安装、卸载、更新、查看、搜索等功能。通过简单的指令可以实现包管理，而不用关心各种依赖和文件路径情况。

二、HomeBrew命令

1、检查是否安装HomeBrew

brew -v

下面是没有安装brew截图：
在这里插入图片描述

2、更新brew版本

brew update

<br

三、安装HomeBrew

1、官网安装

在终端执行如下命令：

/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"

如果安装不上，一般报如下错误：

curl: (7) Failed to connect to raw.githubusercontent.com port 443 after 23 ms: Couldn't connect to server

在这里插入图片描述
无法链接服务器下载，需要梯子，有梯子基本没有问题。

2、100%成功安装

安装指令：

/bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"

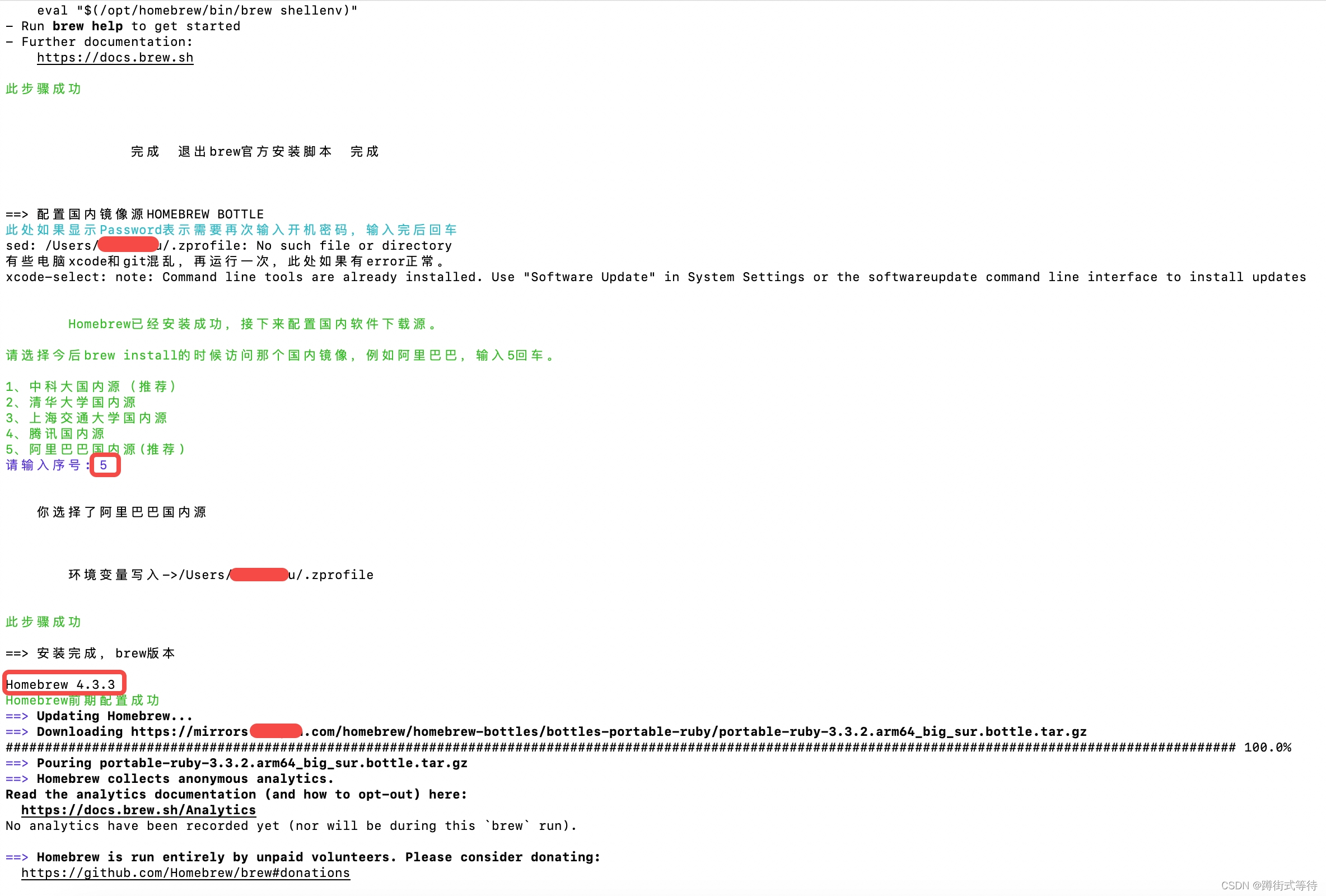
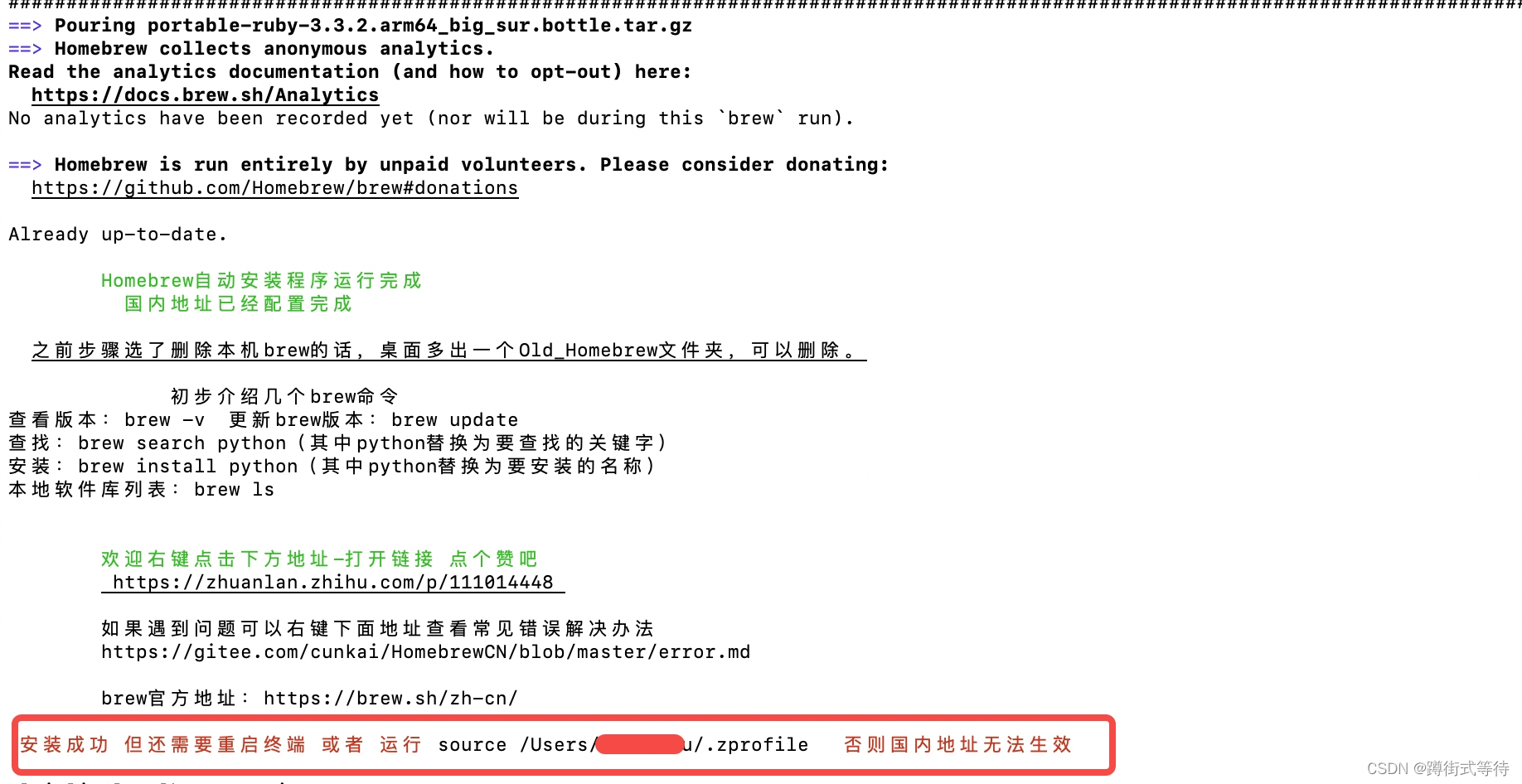
在这里插入图片描述

重启终端之后，执行brew -v命令，正常输出就说明安装成功了。

卸载命令：

/bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/HomebrewUninstall.sh)"

mac 安装HomeBrew

目录一、HomeBrew是什么？二、HomeBrew命令1、检查是否安装HomeBrew2、更新brew版本三、安装HomeBrew1、官网安装2、100%成功安装一、HomeBrew是什么？ homebrew是一款Mac OS平台下的软件包管理工具，拥有安装、卸载、更新、查看、搜索等功能…...

编程日记 2024/6/12 15:53:43

Windows C++: 剪切板内容获取

获取Windows用户的剪切操作是部分程序的需求，我们同样可以利用这个功能做一个小工具来记忆曾经的复制内容。代码示例 if (OpenClipboard(nullptr)) {// 打开剪贴板HANDLE hClipboardData GetClipboardData(CF_UNICODETEXT);// 获取剪贴板中的Unicode文本数据if …...

编程日记 2024/6/12 15:52:42

1panel运维面板

文章目录引言I 安装防火墙II 借助运维面板1panel运维面板安装nacos 引言在 SSH 终端输入以下命令来查看面板入口: 1pctl user-info 提示：修改密码可执行命令：1pctl update password I 安装防火墙 https://1panel.cn/docs/user_manual/hosts/firewall…...

编程日记 2024/6/12 15:51:40

人工智能GPT-4o？

对比分析在讨论GPT-4o时，我们首先需要了解其前身，即GPT-4，以及其之前的版本。GPT系列从GPT-1到GPT-4经历了多次迭代，每一次都带来了显著的进步。 GPT-4 vs GPT-4o： 1. **参数规模：** GPT-4o在参数规模上…...

编程日记 2024/6/12 15:48:37

python之语法糖

一.语法糖语法糖不是糖,而是编程语言中的某些特殊写法,这些写法让书写起来更加简洁,容易理解,因此被叫做语法糖二.语法糖分类数字分隔符 a 10_0000_0000交换变量值 a 1;b 2 a,b b,a连续比较式 a 90 if 80<a<100: print(‘优秀’)字符串乘法 a ‘_’*10列表拼…...

编程日记 2024/6/12 15:46:34

纷享销客海外合规观点与方案：个人隐私数据保护与数据出入境

出海，已不再是企业的“备胎”，而是必须面对的“大考”！在这个全球化的大潮中，有的企业乘风破浪，勇攀高峰，也有的企业在异国他乡遭遇了“水土不服”。面对“要么出海，要么出局”的抉择&#xf…...

编程日记 2024/6/12 15:45:32

公司面试题总结（四）

19.请解释什么是事件代理，应用场景 ⚫ 事件流的都会经过三个阶段： 捕获阶段 -> 目标阶段 -> 冒泡阶段，而事件委托就是在冒泡阶段完成 ⚫ 事件委托，会把一个或者一组元素的事件委托到它的父层或者更外层元素上&#xf…...

编程日记 2024/6/12 15:44:31

守护山川，联通希望 —— 北斗户外应急呼叫柱：野外安全的守护神

在大自然的怀抱中，每一次探险和巡检都是对未知的挑战，也是对安全的考验。北斗户外应急呼叫柱，以科技创新为基石，致力于在最偏远、最危险的环境中搭建起生命的桥梁，确保每一次求救都能被听见，每一处危机都能…...

编程日记 2024/6/12 15:43:29

使用canvas制作一个无人机旋转特效

使用HTML5的Canvas API来制作一个无人机旋转特效。这个特效将包括一个无人机图标（你可以使用任何你喜欢的图标），它会在一个固定的位置旋转。首先，我们需要创建一个HTML文件，然后在其中添加一个canvas元素。canvas…...

编程日记 2024/6/12 15:42:28

感受风的速度~2024COSP上海国际户外展为您的骑行之旅锦上添花

夏天已经到来你是在家里宅着还是出去晒太阳呢若是还没抉择好不如来一场畅快淋漓的追风之旅抬头可见蓝天白云低头便是美丽风景无论是在凉亭闲聊的人们还是竞相绽放的花朵每一个场景都令人难忘骑累了就到附近的座椅上小憩一番不用刻意追求速度尽享“慢…...

编程日记 2024/6/12 15:41:27

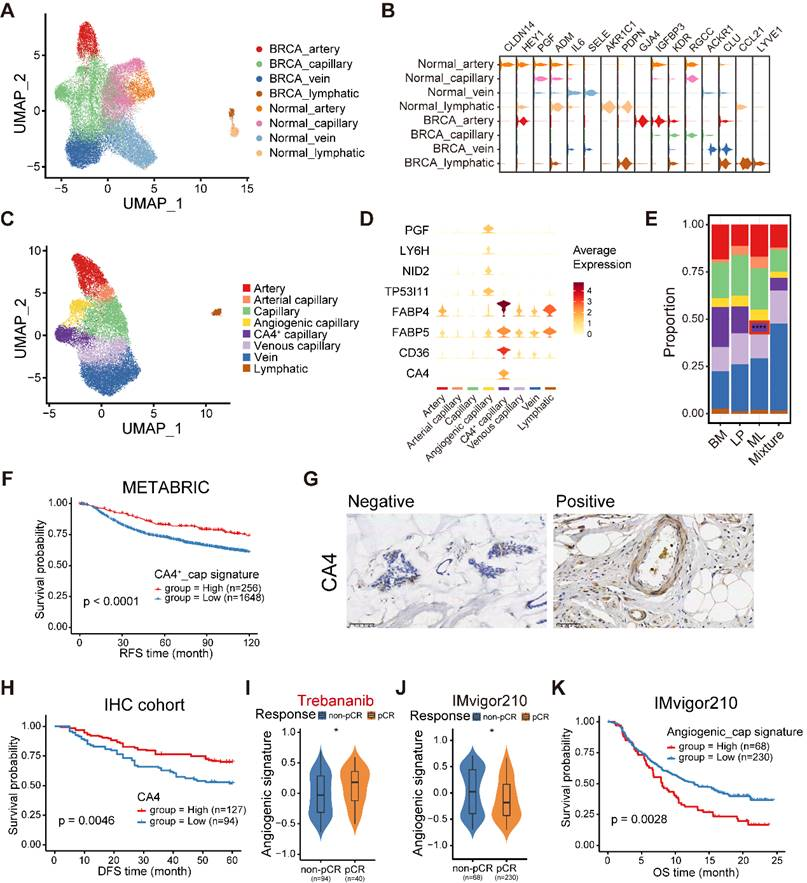
冲12分top刊｜乳腺癌单细胞细分亚型的正确打开方式

说在前面学习一下一篇自测数据工作量叠满的单细胞文章，也算是多组学的了，bulkRNAscRNA，还有个伪RNA。整体是一个单细胞分小群的研究思路，分出三种上皮细胞亚群（BM、LP、ML），在功能、免疫、预…...

编程日记 2024/6/12 15:40:25

1-Maven-settings配置

1-Maven-settings配置整理下Maven工具的使用。【本地仓库、私服、镜像仓库、远程仓库、中央仓库】本文基于阅读其他博客和对公司Maven配置的学习整理出来的。希望通过本此学习能对Maven有个整体性的掌控。顺序：profile.repository > pom文件中的repository &…...

编程日记 2024/6/12 15:39:24

使用服务器搭建个人图床

前置条件云服务器picGo软件，下载地址开始搭建发布站点该步骤不一一说明，主要说明搭建图床的步骤。可以直接使用nginx或者宝塔面板，发布一个静态资源的文件夹。假如我发布的文件路径是/www/img，访问地址是http://cc.cc.cc（没有域名ip地址也行）在img下建立两个文件夹…...

编程日记 2024/6/12 15:34:20

探索 doc 和 docx 文件格式的区别

人不走空 🌈个人主页：人不走空 💖系列专栏：算法专题 ⏰诗词歌赋：斯是陋室，惟吾德馨目录 🌈个人主页：人不走空 💖系列专栏：算法专题 ⏰诗词歌…...

编程日记 2024/6/12 15:33:18

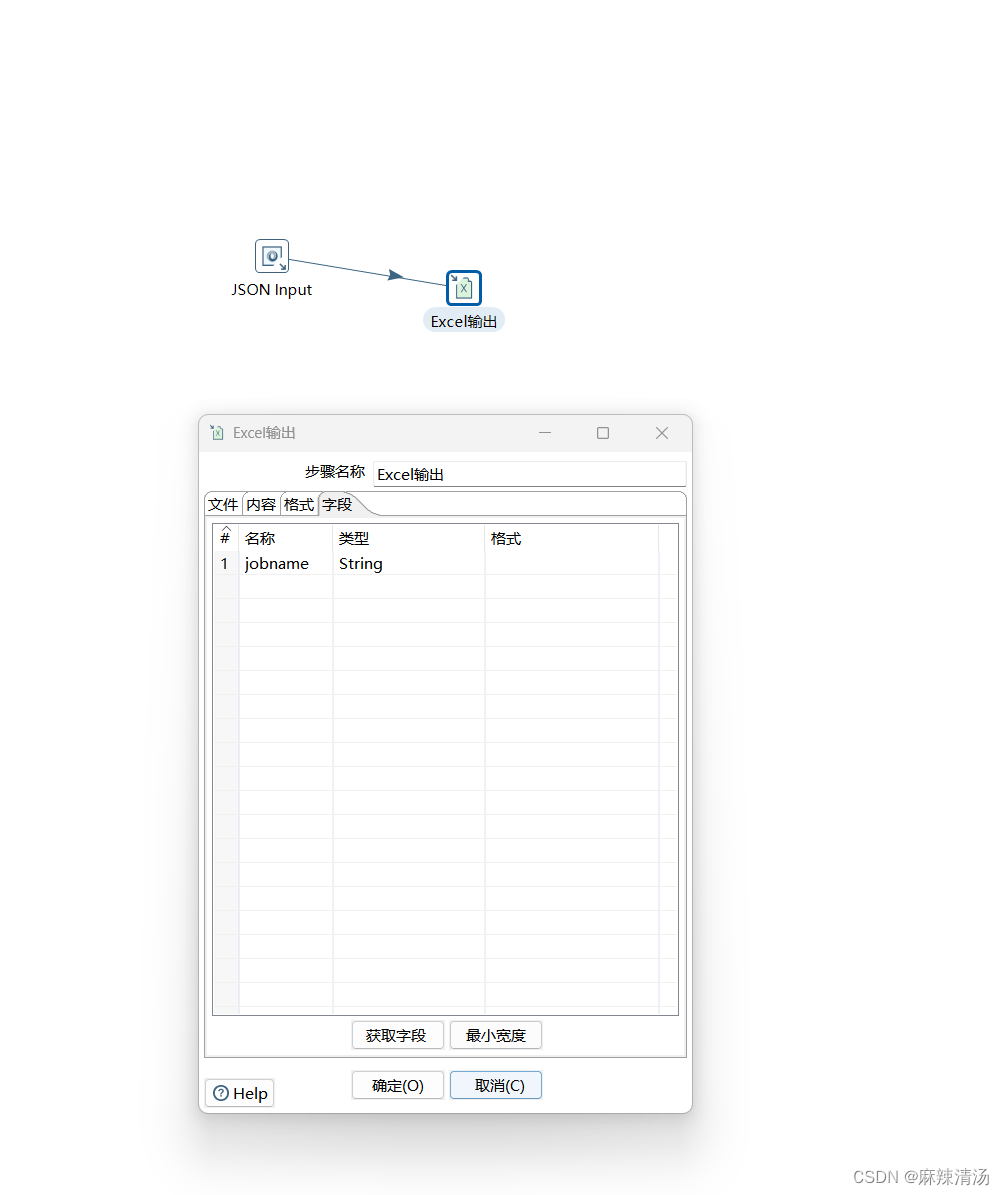
kettle学习（利用jsonPath定位，json文件转换）

kettle学习（利用jsonPath定位，json文件转换） 于数据处理的广袤天地间，我们时常需应对各类繁杂状况与各式格式。Kettle 作为极具威力的数据集成利器，赋予了我们诸多功能与无限可能此次博客里，我们将重点投向…...

编程日记 2024/6/12 15:32:17

选到哪里看命

srand()、rand() srand(static_cast<unsigned int>(time(nullptr))) 是 C 中用于初始化随机数生成器（Random Number Generator, RNG）的一个常用语句。srand 函数是 C 标准库 <cstdlib> 中的一部分，用于设置随机数发生器的种子值…...

编程日记 2024/6/12 15:31:16

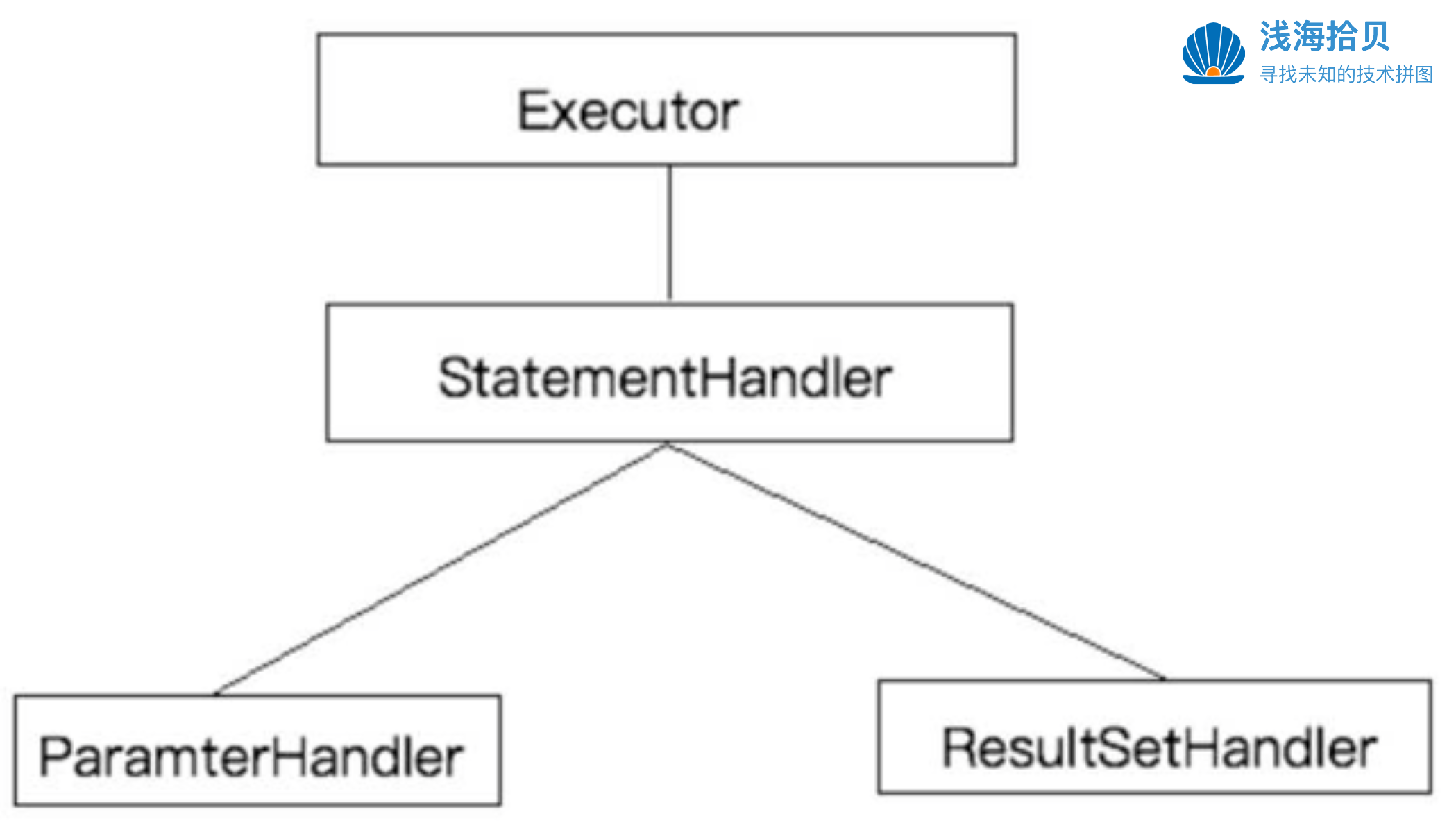
MyBatis插件机制介绍与原理

插件简介什么是插件插件是一种软件组件，可以在另一个软件程序中添加功能或特性。插件通常被设计成可以随时添加或删除的，而不影响主程序的功能。插件可以扩展软件程序的功能，这让用户可以根据自己的需求定制软件，提高工作…...

编程日记 2024/6/12 15:29:13

[每日一练]利用.str.len()布尔值查询实现字数需求

该题目来源于力扣： 1683. 无效的推文 - 力扣（LeetCode） 题目要求： 表：Tweets ------------------------- | Column Name | Type | ------------------------- | tweet_id | int | | content …...

编程日记 2024/6/12 15:28:12

Post Microsoft Build and AI Day 北京开发者日

Microsoft Build 开发者大会 Microsoft Build 开发者大会是微软每年一次的开发者技术盛会，旨在向全球开发者展示微软最新的技术、产品和服务。刚刚过去的 2024 Microsoft Build 开发者大会围绕 Copilot、生成式 AI、应用程序安全、云平台、低代码等多个技术方向&a…...

编程日记 2024/6/12 15:27:11

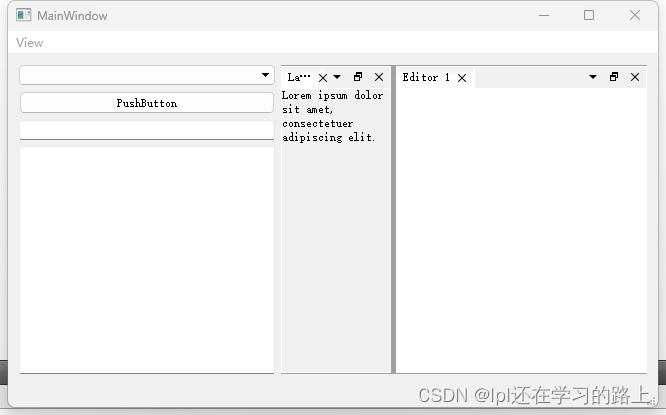
Qt-Advanced-Docking-System的学习

Qt5.12实现Visual Studio 2019 拖拽式Dock面板-Qt-Advanced-Docking-System_c_saide6000-GitCode 开源社区 (csdn.net) 我使用的是Qt5.5.0 开始，我下载的是最新版的源码：4.1版本但是，打开ads.pro工程文件，无法编译成功。然后…...

编程日记 2024/6/12 15:25:08

清华系团队造出能“边听边说、边看边想“的AI耳朵MiniCPM-o 4.5

这项由清华大学自然语言处理实验室（THUNLP）主导、OpenBMB开源社区联合推出的研究成果，于2026年4月30日以预印本形式发布在arXiv平台，编号为arXiv:2604.27393。感兴趣的读者可通过这个编号检索到完整论文。**一场关于"耳朵和嘴…...

编程新知 2026/5/13 1:34:44

1查询整个mysql下数据库大小SELECTtable_schema AS db_name,ROUND(SUM(data_length index_length)/1024/1024,2) AS size_mb FROM information_schema.tables GROUP BY table_schema ORDER BY size_mb DESC;| db_name | size_mb | -------------------------…...

编程新知 2026/5/13 1:01:09