矩阵练习2
48.旋转图像
规律:
对于矩阵中第 i行的第 j 个元素,在旋转后,它出现在倒数第i 列的第 j 个位置。
matrix[col][n−row−1]=matrix[row][col]
可以使用辅助数组,如果不想使用额外的内存,可以用一个临时变量 。
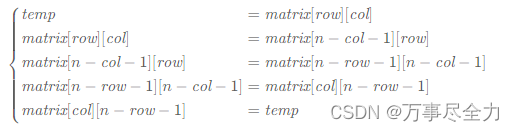
还可以通过水平翻转后再进行主对角线翻转。
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 水平翻转for(int i=0; i<n/2; i++){for(int j=0; j<n; j++){int temp = matrix[i][j];matrix[i][j]=matrix[n-i-1][j];matrix[n-i-1][j]=temp;}}// 主对角线翻转for(int i=0; i<n; i++){for(int j=0; j<i; j++){int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i]=temp;}}}
}240.搜索二维矩阵 II
由于矩阵 matrix中每一行的元素都是升序排列的,因此我们可以对每一行都使用一次二分查找,判断 target 是否在该行中,从而判断 target 是否出现。
也可以采用Z字形查找。
从矩阵 matrix的右上角 (0,n−1)进行搜索。在每一步的搜索过程中,如果我们位于位置 (x,y),那么我们希望在以 matrix 的左下角为左下角、以 (x,y)为右上角的矩阵中进行搜索,即行的范围为 [x,m−1],列的范围为 [0,y]。
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int x=0, y=n-1;while(x<m && y>=0){if(matrix[x][y]==target){return true;}if(matrix[x][y]<target){x++;}else{y--;}}return false;}
}相关文章:
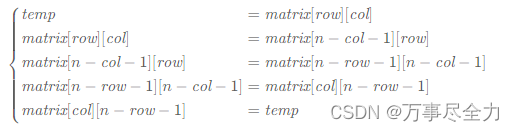
矩阵练习2
48.旋转图像 规律: 对于矩阵中第 i行的第 j 个元素,在旋转后,它出现在倒数第i 列的第 j 个位置。 matrix[col][n−row−1]matrix[row][col] 可以使用辅助数组,如果不想使用额外的内存,可以用一个临时变量 。 还可以通…...
2024海南省大数据教师培训-Hadoop集群部署
前言 本文将详细介绍Hadoop分布式计算框架的来源,架构和应用场景,并附上最详细的集群搭建教程,能更好的帮助各位老师和同学们迅速了解和部署Hadoop框架来进行生产力和学习方面的应用。 一、Hadoop介绍 Hadoop是一个开源的分布式计算框架&…...

力扣算法题:将数字变为0的操作次数--多语言实现
无意间看到,力扣存算法代码居然还得升级vip。。。好吧,我自己存吧 golang: func numberOfSteps(num int) int {steps : 0for num > 0 {if num%2 0 {num / 2} else {num - 1}steps}return steps } javascript: /*** param {number} num…...

vue前段处理时间格式,设置开始时间为00:00:00,设置结束时间为23:59:59
在Vue开发中,要在前端控制日期时间选择器的时间范围,可以通过以下方式实现: 使用beforeDestroy生命周期钩子函数来处理时间范围: 在Vue组件中,可以监听日期时间选择器的变化,在选择开始日期时,自…...

Java 8 新特性全面解读
Java 8,作为一次重大更新,于2014年引入了多项创新特性,极大地改善了Java的编程体验和性能。此版本不仅加入了对函数式编程的支持,还增强了接口的功能,引入了新的API,并优化了语言的整体效率。接下来&#x…...

JavaScript知识之函数
javascript函数 在JavaScript基础之上提供了部分函数,同时也可以自定义函数,JavaScript基础详见之前的文章javascript基础知识 自定义函数 //关键字 函数名 参数列表 函数体 function test(a,b,c){alert(a":"b":"c) }function test1(a,b){return a;//不…...

【Pepper机器人开发与应用】一、Pepper SDK for LabVIEW下载与安装教程
🏡博客主页: virobotics(仪酷智能):LabVIEW深度学习、人工智能博主 📑上期文章:『一文汇总对比英伟达、AMD、英特尔显卡GPU』 🍻本文由virobotics(仪酷智能)原创 🥳欢迎大家关注✌点赞&…...

HCIP-AI EI 认证课程大纲
该阶段详细介绍计算机视觉、注意力机制与Transformer、自然语言处理、语音处理等 AI 核心领域技术,并重点介绍华为云 EI 服务使用。 共计48 课时。第一节:计算机视觉技术概述与图像处理基础 - (3 课时) - 什么是计算机视觉&#x…...
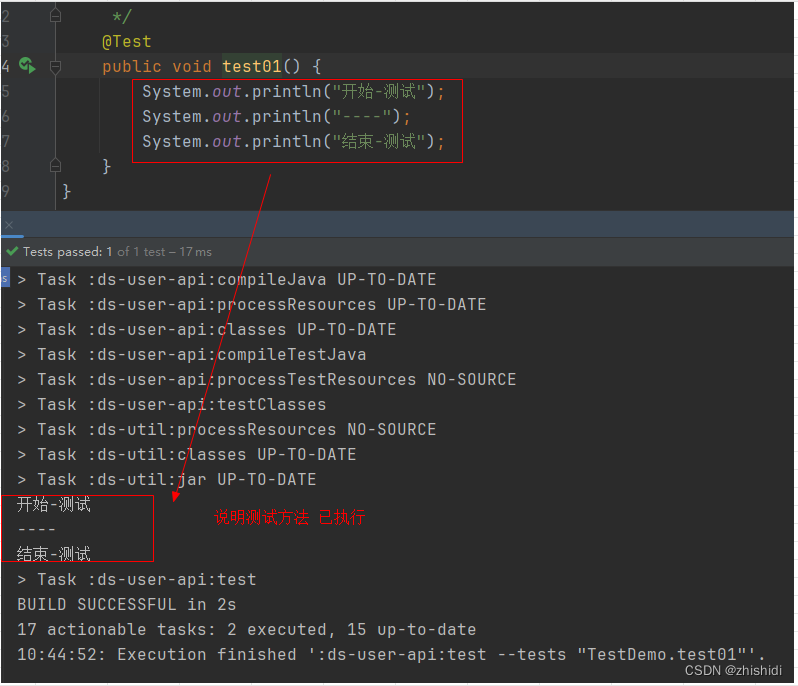
@Test注解方法,方法无法执行
1.背景 写了一个测试方法,执行后如图 2.原因是 该项目是springbootgradle...构建的项目 在build.gradle配置文件中关闭了单元测试: test {useJUnitPlatform()// 是否启用单元测试enabled false } 3.处理方式 开启单元测试 test {useJUnitPlatform()// 是否启用单元测试ena…...
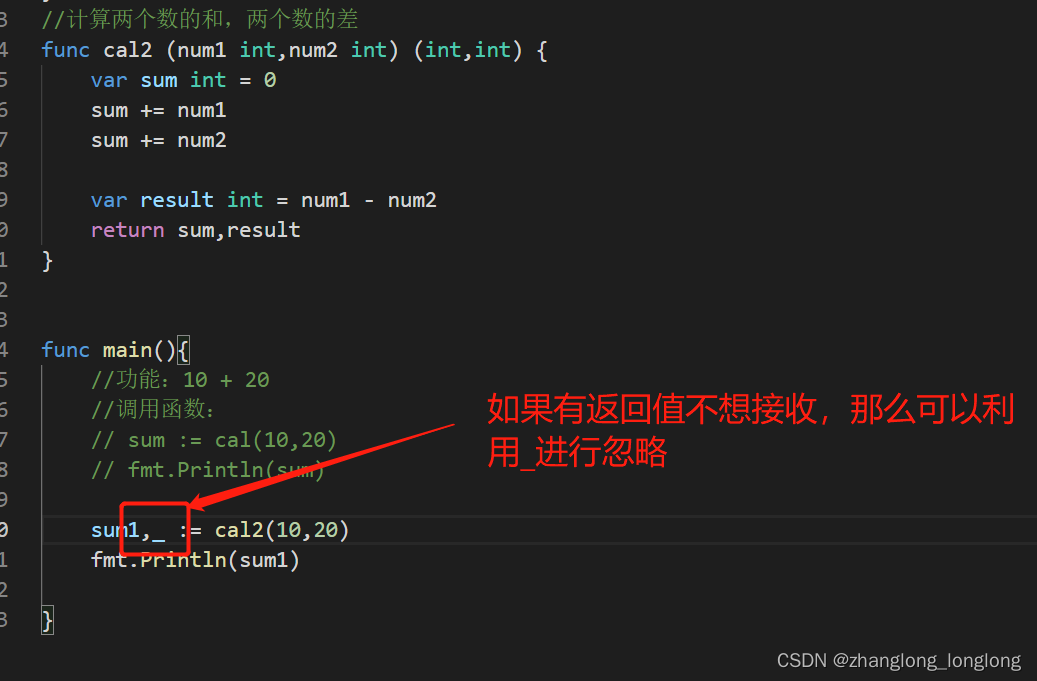
golang函数
【1】函数: 对特定的功能进行提取,形成一个代码片段,这个代码片段就是我们所说的函数 【2】函数的作用:提高代码的复用性 【3】函数和函数是并列的关系,所以我们定义的函数不能写到main函数中 【4】基本语法 func 函…...

ubuntu上存在多个版本python,根据需要选择你想使用的python版本
文章目录 前言一、二、使用步骤总结 前言 参考1 一、 sudo update-alternatives --install /usr/bin/python python /usr/bin/python3.6 1二、使用步骤 总结...

idea 常用插件推荐
文章目录 1、Lombok2、Convert YAML and Properties File3、Grep Console4、MyBatisX5、Free MyBatis Tool6、MyBatis Log EasyPlus (SQL拼接)7、MyBatisPlus8、Eclipse theme9、Eclipse Plus Theme10、Rainbow Brackets Lite - Free and OpenSource&…...
训练大模型自动在RAG和记忆间选择
现如今,检索增强生成(Retrieval-augmented generation,RAG)管道已经能够使得大语言模型(Large Language Models,LLM)在其响应环节中,充分利用外部的信息源了。不过,由于RAG应用会针对发送给LLM的每个请求,都…...

抖店没人做了?不是项目不行了,而是商家们都换思路去玩了
我是王路飞。 有没有发现现在很多抖店新手都在吐槽,抖店不好做了,做不起来,没人做了,太内卷了...... 对这种做不起来还在怪项目本身的,一定要离他远一点,省得被他的负能量给影响到自己的状态。 任何项目…...

Qt5.15.2+VS2019新加类出现无法解析的外部符号
Qt5.15.2VS2019新加类出现无法解析的外部符号: 原因:没有生成对应的moc文件,导致没生成对应的元对象。 解决方案:记事本打开工程vcxproj,把报错的文件ClInclude,改为QtMoc,解决问题 未修改前&…...
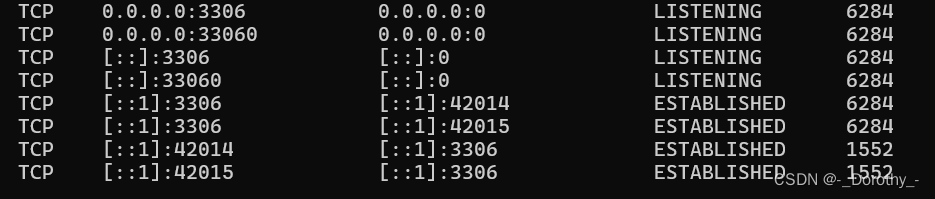
启动mysql 3.5时出现 MySql 服务正在启动 . MySql 服务无法启动。
有可能是端口冲突 netstat -ano | findstr :3306运行这段代码出现类似: 可以看到端口 3306 已经被进程 ID 为 6284 的进程占用。为了启动新的 MySQL 服务,我们需要停止这个进程或更改新服务的端口: 1、终止进程 taskkill /PID 6284 /F2、确…...
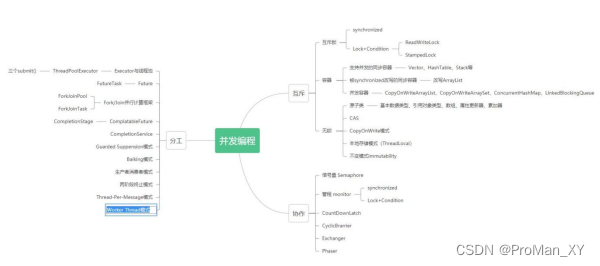
并发编程理论基础——可见性、原子性和有序性问题(一)
核心问题:分工,同步,互斥 分工:如何高效地拆解任务并分配给线程 生产者-消费者模式、Thread-Per-Message模式、Worker-Thread模式、ComplateableFuture和CompletionServiceJava SDK 并发包里的 Executor、Fork/Join、Future 本质上…...

心理咨询系统源码|心理咨询系统开发|心理咨询系统
心理咨询系统,作为一种集现代化科技与专业心理服务于一体的工具,正逐渐渗透到我们生活的各个角落。它不仅为个人提供了便捷的心理支持,还为企业和组织带来了全新的管理方式。下面,我们将深入探讨心理咨询系统的可应用范围及其带来…...
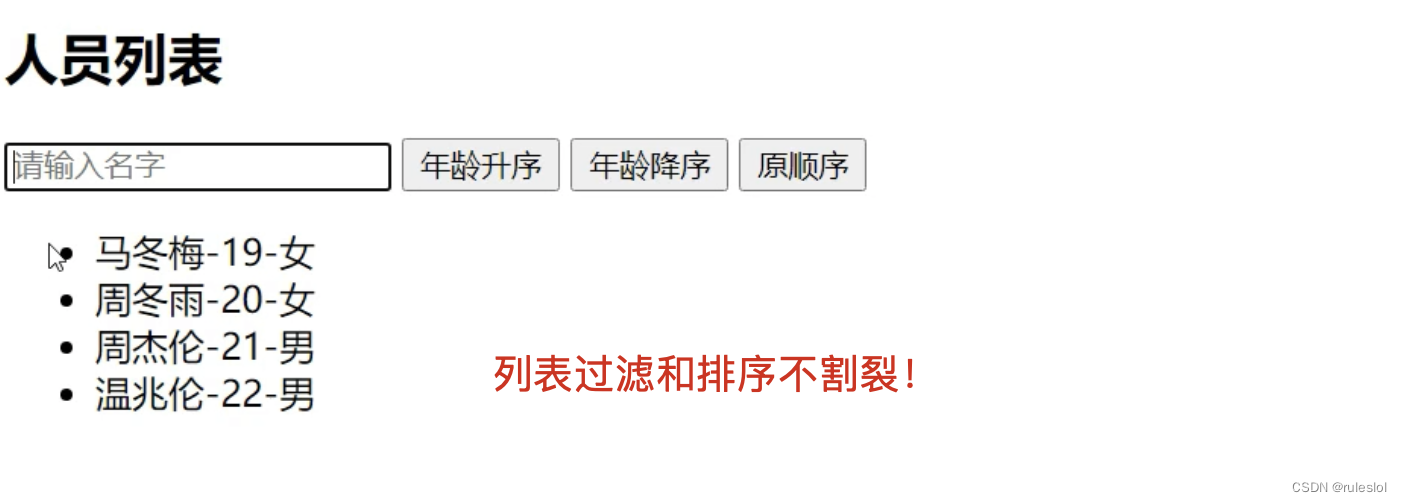
Vue21-列表排序
一、需求 二、解决方式 <body><div id"root"><h2>人员列表</h2><input type"text" placeholder"请输入" v-model"keyword"><button click"sortType 1">年龄升序</button><b…...

配置 JDK 和 Android SDK
目录 一、配置JDK 1. 安装 JDK 2. JDK 环境配置 3. JDK的配置验证 二、配置 adb 和Android SDK环境 1、下载 2、配置 Android SDK 环境 一、配置JDK 1. 安装 JDK 安装链接:Java Downloads | Oracle 我安装的是 .zip ,直接在指定的文件夹下解压就…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
