169. 多数元素
题目
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
- 输入:
nums = [3,2,3] - 输出:
3
示例 2:
- 输入:
nums = [2,2,1,1,1,2,2] - 输出:
2
提示:
n == nums.length1 <= n <= 5 * 10^4-10^9 <= nums[i] <= 10^9
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
代码
完整代码
int majorityElement(int* nums, int numsSize) {int most = nums[0];int cnt = 1;for (int i = 1; i < numsSize; i++) {if (nums[i] == most) {cnt++;} else {cnt--;if (cnt < 0) {most = nums[i];cnt = 1;}}}return most;
}
思路分析
该问题的最优解法是使用Boyer-Moore多数投票算法,时间复杂度为 O(n),空间复杂度为 O(1)。这个算法的核心思想是维护一个候选多数元素以及其计数器。当遍历数组时,如果当前元素与候选多数元素相同,计数器加一;如果不同,计数器减一。当计数器减为零时,将当前元素设为候选多数元素,并重置计数器为一。最终剩下的候选多数元素即为数组中的多数元素。
拆解分析
初始化候选元素和计数器
初始化候选多数元素 most 为数组的第一个元素,计数器 cnt 为 1。
int most = nums[0];
int cnt = 1;
遍历数组更新候选元素和计数器
遍历数组,从第二个元素开始:
- 如果当前元素等于候选多数元素,计数器加一;
- 否则,计数器减一;
- 如果计数器减为零,更新候选多数元素为当前元素,并重置计数器为一。
for (int i = 1; i < numsSize; i++) {if (nums[i] == most) {cnt++;} else {cnt--;if (cnt < 0) {most = nums[i];cnt = 1;}}
}
返回候选多数元素
最终返回候选多数元素 most。
return most;
复杂度分析
- 时间复杂度:O(n),其中 n 是数组的长度。我们只需遍历数组一次。
- 空间复杂度:O(1),我们只使用了常数级别的额外空间。
结果
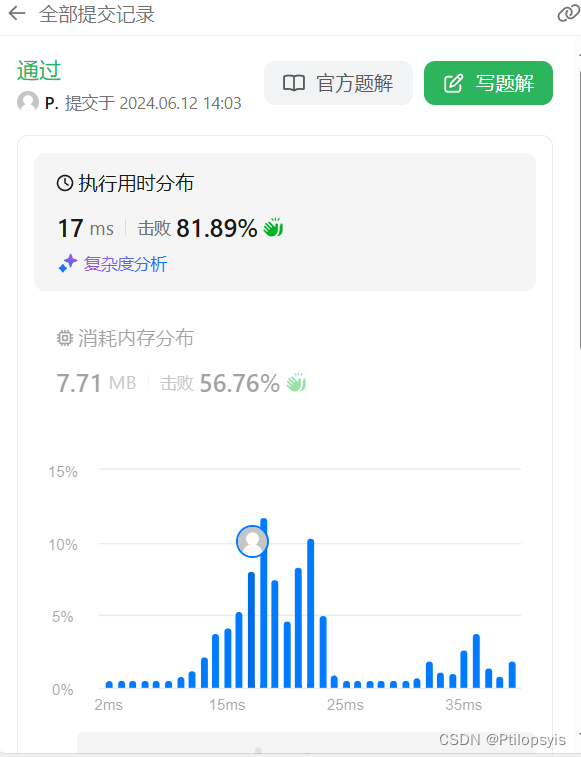
一题多解
排序法
排序法思路分析
排序数组后,多数元素必定会出现在中间位置。我们可以直接返回排序后的数组中位于 n/2 位置的元素。
排序法复杂度分析
- 时间复杂度:O(n log n),这是
qsort的时间复杂度。 - 空间复杂度:O(1),如果排序算法是原地排序,否则为 O(n)。
完整代码
#include <stdio.h>
#include <stdlib.h>int cmp(const void* a, const void* b) {return (*(int*)a - *(int*)b);
}int majorityElement(int* nums, int numsSize) {qsort(nums, numsSize, sizeof(int), cmp);return nums[numsSize / 2];
}
拆解分析
排序数组
使用标准库中的 qsort 函数对数组进行排序。
qsort(nums, numsSize, sizeof(int), cmp);
返回中间元素
由于多数元素必定会出现在中间位置,直接返回排序后数组中 numsSize / 2 位置的元素。
return nums[numsSize / 2];
结果
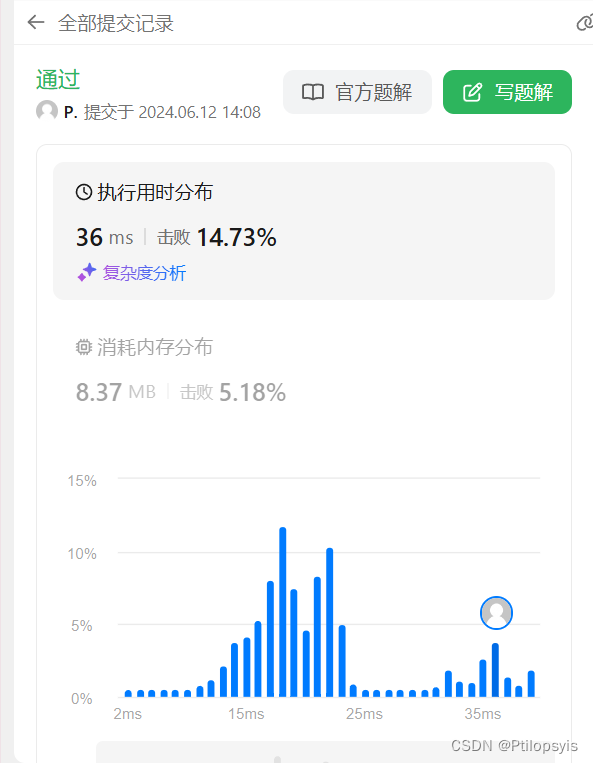
相关文章:

169. 多数元素
题目 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3]输出:3 …...

ADS基础教程19 - 电磁仿真(EM)基本概念和实操
EM介绍 一、引言二、基本概念1.EM介绍2.Momentum介绍3.FEM介绍4.Substrate介绍 三、创建Layout并进行Momentum仿真1.创建Layout2.添加Microtrip(微带线)3.添加Substrate4.Momentum仿真 四、总结 一、引言 本章节开始介绍EM的基本概念、内容以及实现具体…...
LabVIEW RT环境中因字符串拼接导致的系统崩溃问题
在LabVIEW实时操作系统(RT)环境中运行的应用程序出现字符串拼接后死机的问题,通常涉及内存管理、内存泄漏或其他资源管理问题。以下是一些指导和步骤,帮助解决这个问题: 1. 内存泄漏检测 字符串拼接会在内存中创建新…...
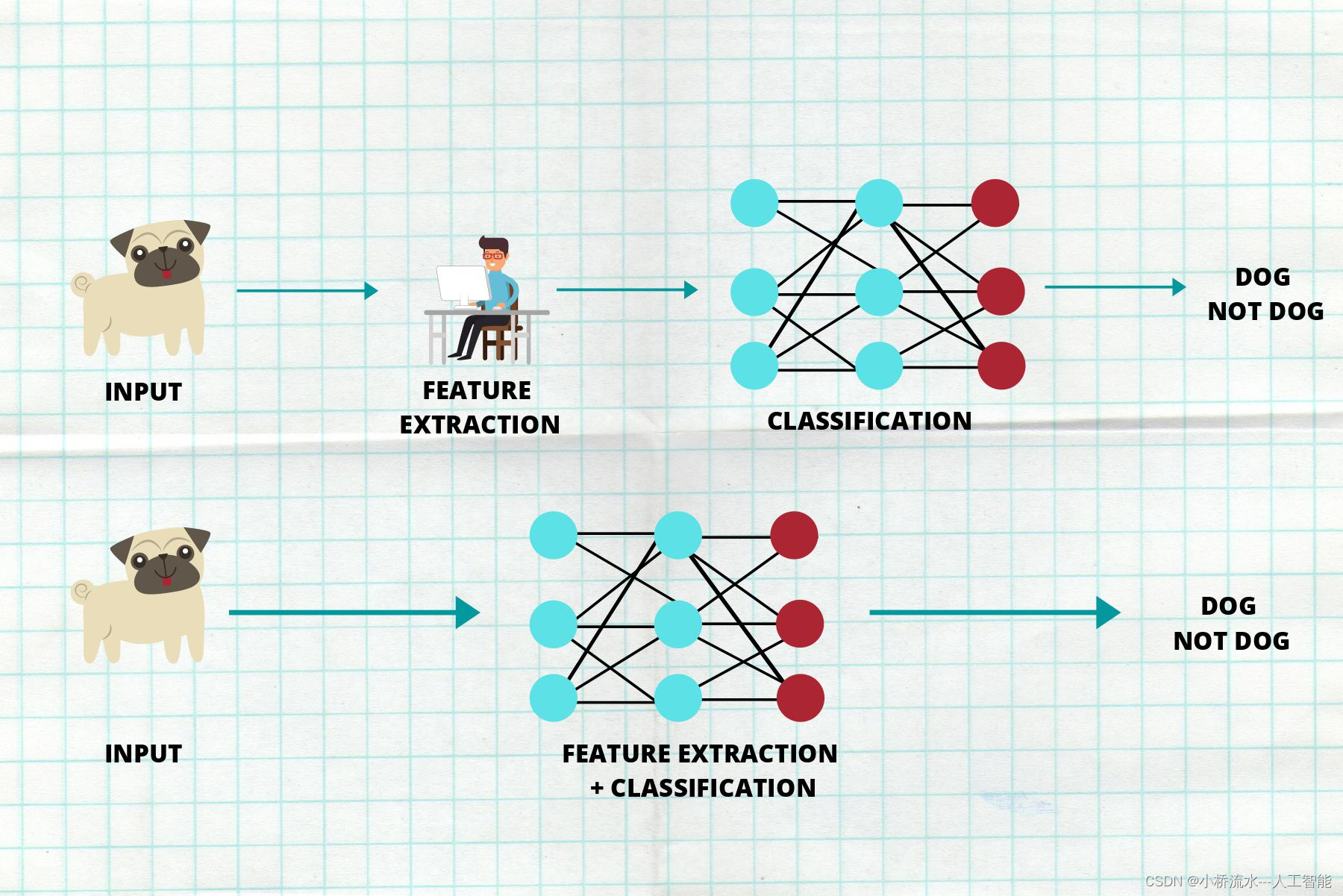
深层网络:层数多真的更好吗?
深层网络:层数多真的更好吗? 在深度学习的世界里,"深度"始终是一个热门话题。随着技术的发展,我们有了越来越多的方法来构建更深的神经网络,这似乎暗示着“层数越多,效果越好”。然而࿰…...
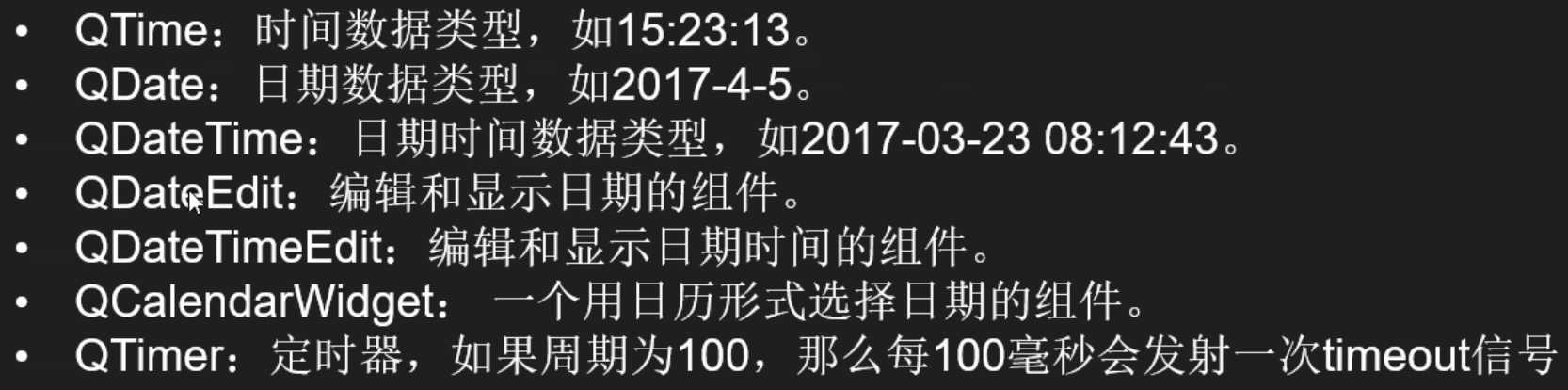
【QT5】<知识点> QT常用知识(更新中)
目录 一、更改文本颜色和格式 二、QT容器类 三、字符串与整数、浮点数之间的转换 四、QString常用功能 五、SpinBox的属性介绍 六、滑动、滚动、进度条和表盘LCD 七、时间、日期、定时器 一、更改文本颜色和格式 动态设置字体粗体:QFont对象的setBold方法动态…...

如何将AndroidStudio和IDEA的包名改为分层级目录
新版UIAndroidStudio 1、点击项目目录右上角如图所示的三个点点。 2、然后依次取消Hide empty middle package ,Flatten package的勾选 3、注意:一定要先取消hide的勾选,不然目录不会完全分级(做错了可以反过来重新设置&#x…...
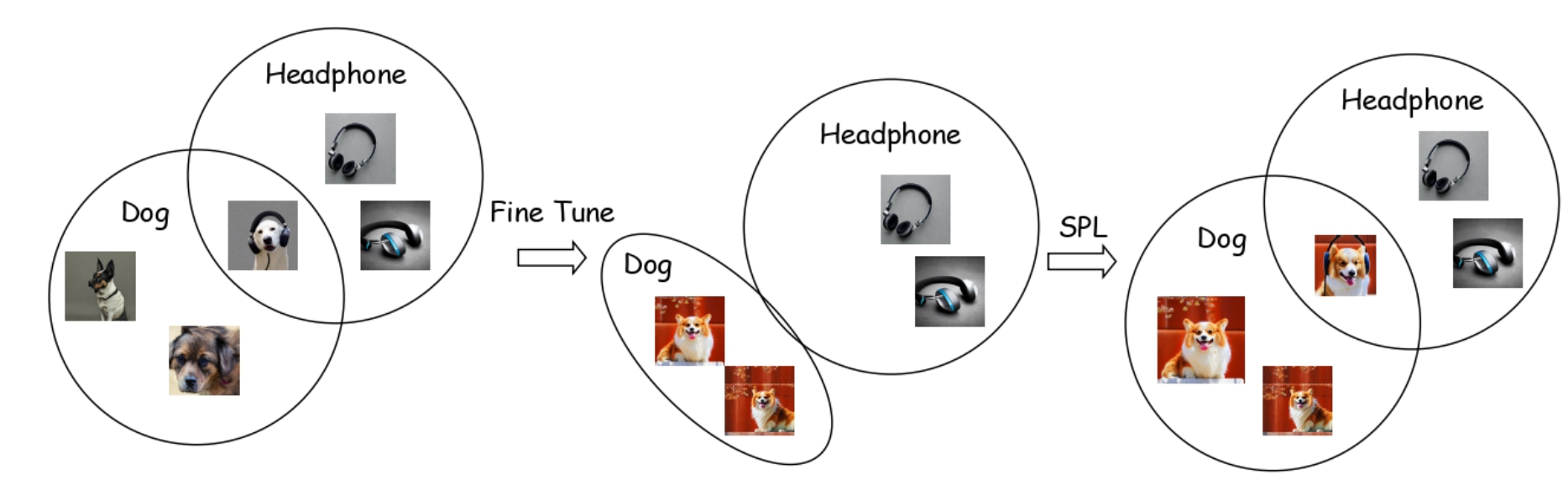
北交字节联合提出ClassDiffusion: 使用显式类别引导的一致性个性化生成。
在个性化生成领域, 微调可能会引起过拟合导致模型无法生成与提示词一致的结果。针对这个问题,北交&字节联合提出ClassDiffusion,来提升个性化生成的一致性。 通过两个重要观察及理论分析提出了新的观点:一致性的损失是个性化概念语义偏移导致的, 还…...

37、matlab矩阵运算
1、前言 矩阵运算是指对矩阵的各种操作和运算,包括矩阵加法、矩阵减法、矩阵乘法、矩阵转置、求逆矩阵等。以下是常见的矩阵运算: 矩阵加法:对应位置的元素相加,要求加数和被加数的维度相同。 A B | a11 b11 | | a12 b12 | | …...

用软件实现的硬件——虚拟机
通过软件实现CPU和内存等硬件所具有的功能,并在计算机中运行循环的计算机技术称为虚拟机。使用虚拟机,就可以在一台计算机中运行多个循环出来的计算机。 近几年的计算机,除了硬件具有较高的性能外,CPU的性能也有了提升。因此&…...
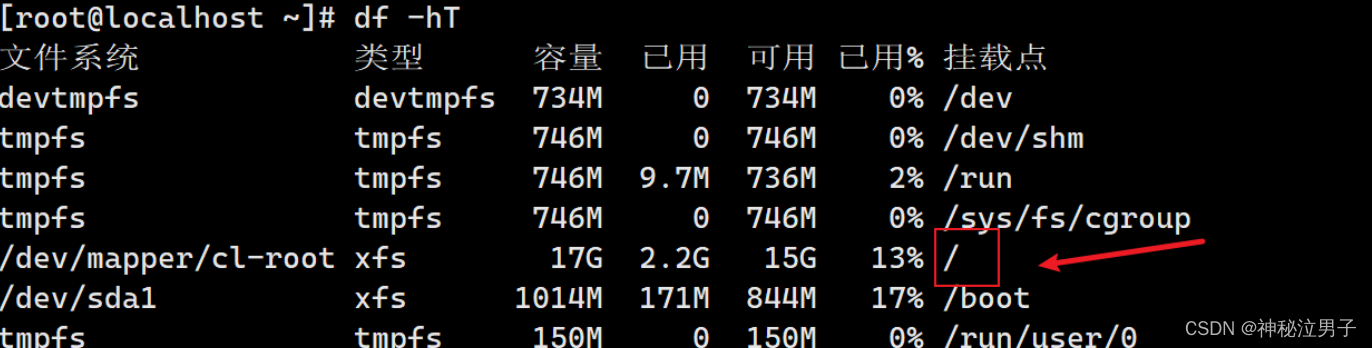
[Shell编程学习路线]--shell中重定向和管道符(详细介绍)
🏡作者主页:点击! 🛠️Shell编程专栏:点击! ⏰️创作时间:2024年6月12日10点50分 🀄️文章质量:93分 ——前言—— 在Shell编程中,重定向和管道符是两个…...

Linux命令详解(1)
在Linux操作系统中,命令行界面(CLI)是一个强大的工具,它允许用户通过键入命令来与系统交互。无论是系统管理员还是普通用户,掌握一些基本的Linux命令都是非常重要的。在本文中,我们将探讨一些常用的Linux命…...

网工内推 | 深信服、中软国际技术支持工程师,最高13k*13薪
01 深信服 🔷招聘岗位:远程技术支持工程师 🔷任职要求: 一、专业能力和行业经验: ①具备友商同岗位工作经验1.5年以上,具备良好的分析和判断能力,有独立问题处理思路,具备常见协…...

实现卡片的展开缩放动画
原理,外层包裹一个元素,子元素分别是展开和收起的元素,然后对展开的元素添加动画,动画内容是随时间变化,将卡片的transform:rotateX属性进行调整,因为改变的是子元素的旋转,父元素高…...

实验:贪心算法
实验二:贪心算法 【实验目的】 应用贪心算法求解活动安排问题。 【实验性质】 验证性实验。 【实验要求】 活动安排问题是可以用贪心算法有效求解的很好的例子。 问题:有n个活动的集合A{1,2,…,n},其中每个活动都要求使用同一资源&…...

Python学习笔记12 -- 有关布尔值的详细说明
一、布尔表达式 最终值为true 或者false 二、常见形式: 1、常量:true false 2、比较运算: and ! 3、复合运算: and and or 4、其他 例:检测闰年: def specialYearMine(year):if (year%4 …...

SQL-窗口函数合集
目录 1.窗口函数简介2.窗口的定义3.相关题目示例3.1 PERCENT_RANK()2346 以百分比计算排名 3.2 FIRST_VALUE()/LAST_VALUE()/NTH_VALUE()2388 将表中的空值更改为前一个值 1.窗口函数简介 MySQL 开窗函数(Window Functions)是 MySQL 8.0 版本引入的一个…...

2024 全球软件研发技术大会官宣,50+专家共话软件智能新范式!
2024年的全球软件研发技术大会(SDCon)由CSDN和高端IT咨询与教育平台Boolan联合主办,将于7月4日至5日在北京威斯汀酒店举行。本次大会的主题为“大模型驱动软件智能化新范式”,旨在探讨大模型和开源技术的发展如何引领全球软件研发…...
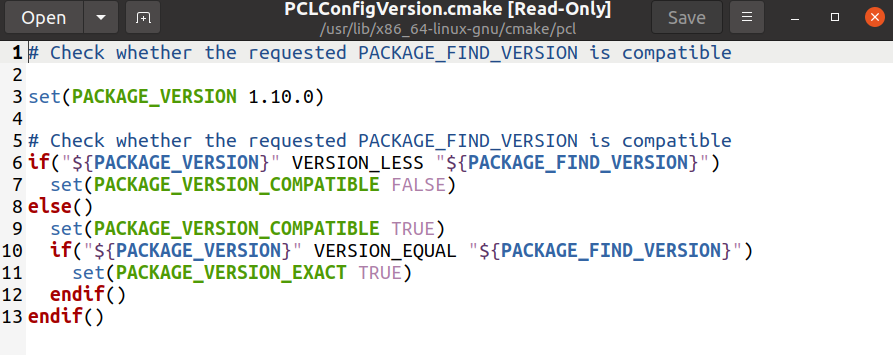
opencv快速安装以及各种查看版本命令
安装opencv并查看其版本,直接通过一个可执行文件实现。 #!/bin/bashwget https://codeload.github.com/opencv/opencv/zip/3.4 -O opencv-3.4.zip && unzip opencv-3.4.zip && cd opencv-3.4 && \mkdir build && cd build &&a…...
免费学习通刷课(免费高分)Pro版
文章目录 概要整体架构流程小结 概要 关于上一版的免费高分的学习通刷课,有很多人觉得还得登录太复杂了,然后我又发现了个神脚本,操作简单,可以后台挂着,但是还是建议调整速度到2倍速,然后找到你该刷的课&…...

线性数据结构-队列
队列(Queue)是一种先进先出(First In First Out, FIFO)的数据结构,它按照元素进入的顺序来处理元素。队列的基本操作包括: enqueue:在队列的末尾添加一个元素。dequeue:移除队列的第…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
