OpenCV学习(4.11) OpenCV中的图像转换
1. 目标
在本节中,我们将学习
- 使用OpenCV查找图像的傅立叶变换
- 利用Numpy中可用的FFT功能
- 傅立叶变换的一些应用
- 我们将看到以下函数:**cv.dft()** ,**cv.idft()** 等
理论
傅立叶变换用于分析各种滤波器的频率特性。对于图像,使用 2D离散傅里叶变换(DFT) 查找频域。快速算法称为 快速傅立叶变换(FFT) 用于计算DFT。关于这些的详细信息可以在任何图像处理或信号处理教科书中找到。请参阅其他资源_部分。
对于正弦信号,$x(t)=Asin(2\pi ft)$ ,我们可以说 $f$ 是信号的频率,如果采用其频域,我们可以在 $f$ 处看到一个尖峰。如果信号进行采样,以形成离散信号,我们得到了相同的频域,但在范围周期性 $[-π,π]$ 或 $[0,2\pi]$(或 $[0,N]$ 用于N点DFT)。您可以将图像视为在两个方向上采样的信号。因此,在X和Y方向都进行傅立叶变换,可以得到图像的频率表示。
更直观地说,对于正弦信号,如果振幅在短时间内变化如此之快,则可以说它是高频信号。如果变化缓慢,则为低频信号。您可以将相同的想法扩展到图像。图像中的振幅在哪里急剧变化?在边缘点或噪音。因此,可以说边缘和噪声是图像中的高频内容。如果幅度没有太大变化,则它是低频分量。(一些链接已添加到“其他资源”,其中通过示例直观地说明了频率变换)。
现在,我们将看到如何找到傅立叶变换。
2.Numpy中的傅里叶变换
首先,我们将看到如何使用Numpy查找傅立叶变换。Numpy具有FFT软件包来执行此操作。np.fft.fft2() 为我们提供了频率转换,它将是一个复杂的数组。它的第一个参数是输入图像,即灰度图像。第二个参数是可选的,它决定输出数组的大小。如果它大于输入图像的大小,则在计算FFT之前用零填充输入图像。如果小于输入图像,将裁切输入图像。如果未传递任何参数,则输出数组的大小将与输入的大小相同。
现在,一旦获得结果,零频率分量(DC分量)将位于左上角。如果要使其居中,则需要将结果偏移 $\frac{N}{2}$ 在两个方向上。只需通过函数 np.fft.fftshift() 即可完成。(它更容易分析)。找到频率变换后,就可以找到幅度谱。
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('messi5.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()结果如下:

看,您可以在中心看到更多白色区域,这表明低频内容更多。
因此,您已经进行了频率变换,您可以在频域中执行一些操作,例如高通滤波和重建图像,若进行逆DFT。为此,您需用尺寸为60x60的矩形窗口遮罩来消除低频。然后,使用 np.fft.ifftshift() 应用反向移位,以使DC分量再次出现在左上角。然后使用 np.ifft2() 函数找到逆FFT 。同样,结果将是一个复数。您可以采用其绝对值来进行
rows, cols = img.shape
crow,ccol = rows//2 , cols//2
fshift[crow-30:crow+31, ccol-30:ccol+31] = 0
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.real(img_back)
plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(img_back, cmap = 'gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()结果如下:

结果表明高通滤波是边缘检测操作。这就是我们在“图像渐变”一章中看到的。这也表明大多数图像数据都存在于频谱的低频区域。无论如何,我们已经看到了如何在Numpy中找到DFT,IDFT等。现在,让我们看看如何在OpenCV中进行操作。
如果您仔细观察结果,尤其是最后一张JET颜色的图像,您会看到一些伪像(我用红色箭头标记的一个实例)。它在那里显示出一些波纹状结构,称为 振铃效应 。这是由我们用于遮罩的矩形窗口引起的。此蒙版转换为正弦形状,从而导致此问题。因此,矩形窗口不用于过滤。更好的选择是高斯窗口。
3. OpenCV中傅里叶变换
OpenCV 为此提供了功能 cv.dft() 和 cv.idft() 。它返回与以前相同的结果,但是有两个通道。第一个通道将具有结果的实部,第二个通道将具有结果的虚部。输入的图像应首先转换为np.float32 。我们将看到如何做。
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('messi5.jpg',0)
dft = cv.dft(np.float32(img),flags = cv.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()注意 您还可以使用 cv.cartToPolar() 一次返回大小和相位
因此,现在我们必须进行逆DFT。在上一部分中,我们创建了一个HPF,这次我们将看到如何去除图像中的高频内容,即我们将LPF应用于图像。实际上会使图像模糊。为此,我们首先创建一个在低频时具有高值(1)的蒙版,即,我们传递LF含量,并在HF区域传递0。
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv.idft(f_ishift)
img_back = cv.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()查看结果:

注意 像往常一样,OpenCV函数 cv.dft() 和 cv.idft() 比Numpy对应函数要快。但是Numpy功能更加人性化。有关性能问题的更多详细信息,请参阅以下部分。
4. DFT的性能优化
对于某些阵列大小,DFT计算的性能更好。当阵列大小为2的幂时,它是最快的。大小为2、3和5的乘积的数组也得到了有效处理。因此,如果您担心代码的性能,可以在找到DFT之前将数组的大小修改为任何最佳大小(通过填充零)。对于OpenCV,您必须手动填充零。但是对于Numpy,您可以指定FFT计算的新大小,它将自动为您填充零。
那么我们如何找到这个最佳尺寸呢?OpenCV 为此提供了一个函数 cv.getOptimalDFTSize() 。它适用于 cv.dft() 和 np.fft.fft2() 。让我们使用IPython magic命令timeit检查它们的性能。
In [16]: img = cv.imread('messi5.jpg',0)
In [17]: rows,cols = img.shape
In [18]: print("{} {}".format(rows,cols))
342 548
In [19]: nrows = cv.getOptimalDFTSize(rows)
In [20]: ncols = cv.getOptimalDFTSize(cols)
In [21]: print("{} {}".format(nrows,ncols))
360 576参见,将大小(342,548)修改为(360,576)。现在让我们用零填充(对于OpenCV),并找到其DFT计算性能。您可以通过创建一个新的大零数组并将数据复制到其中来完成此操作,或者使用 cv.copyMakeBorder() 。
nimg = np.zeros((nrows,ncols))
nimg[:rows,:cols] = img要么:
right = ncols - cols
bottom = nrows - rows
bordertype = cv.BORDER_CONSTANT #just to avoid line breakup in PDF file
nimg = cv.copyMakeBorder(img,0,bottom,0,right,bordertype, value = 0)现在,我们计算Numpy函数的DFT性能比较:
In [22]: %timeit fft1 = np.fft.fft2(img)
10 loops, best of 3: 40.9 ms per loop
In [23]: %timeit fft2 = np.fft.fft2(img,[nrows,ncols])
100 loops, best of 3: 10.4 ms per loop它显示了4倍的加速。现在,我们将尝试使用OpenCV函数。
In [24]: %timeit dft1= cv.dft(np.float32(img),flags=cv.DFT_COMPLEX_OUTPUT)
100 loops, best of 3: 13.5 ms per loop
In [27]: %timeit dft2= cv.dft(np.float32(nimg),flags=cv.DFT_COMPLEX_OUTPUT)
100 loops, best of 3: 3.11 ms per loop它还显示了4倍的加速。您还可以看到OpenCV函数比Numpy函数快3倍左右。也可以对逆FFT进行测试,这留给您练习。
5. 为什么拉普拉斯算子是高通滤波器?
在论坛上提出了类似的问题。问题是,为什么拉普拉斯算子是高通滤波器?为什么Sobel是HPF?等等。第一个得到的答案是傅里叶变换。只需对Laplacian进行傅立叶变换,以获得更大的FFT大小。分析一下:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# simple averaging filter without scaling parameter
mean_filter = np.ones((3,3))
# creating a gaussian filter
x = cv.getGaussianKernel(5,10)
gaussian = x*x.T
# different edge detecting filters
# scharr in x-direction
scharr = np.array([[-3, 0, 3],[-10,0,10],[-3, 0, 3]])
# sobel in x direction
sobel_x= np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])
# sobel in y direction
sobel_y= np.array([[-1,-2,-1],[0, 0, 0],[1, 2, 1]])
# laplacian
laplacian=np.array([[0, 1, 0],[1,-4, 1],[0, 1, 0]])
filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \'sobel_y', 'scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
for i in xrange(6):plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()查看结果:

从图像中,您可以看到每个内核阻止的频率区域以及它经过的区域。从这些信息中,我们可以说出为什么每个内核都是HPF或LPF
相关文章:

OpenCV学习(4.11) OpenCV中的图像转换
1. 目标 在本节中,我们将学习 使用OpenCV查找图像的傅立叶变换利用Numpy中可用的FFT功能傅立叶变换的一些应用我们将看到以下函数:**cv.dft()** ,**cv.idft()** 等 理论 傅立叶变换用于分析各种滤波器的频率特性。对于图像,使用…...

2024.6.13每日一题
LeetCode 子序列最大优雅度 题目链接:2813. 子序列最大优雅度 - 力扣(LeetCode) 题目描述 给你一个长度为 n 的二维整数数组 items 和一个整数 k 。 items[i] [profiti, categoryi],其中 profiti 和 categoryi 分别表示第 i…...

Linux命令详解(2)
文本处理是Linux命令行的重要应用之一。通过一系列强大的命令,用户可以轻松地对文本文件进行编辑、查询和转换。 cat: 这个命令用于查看文件内容。它可以一次性显示整个文件,或者分页显示。此外,cat 还可以用于合并多个文件的内容…...

iOS ReactiveCocoa MVVM
学习了在MVVM中如何使用RactiveCocoa,简单的写上一个demo。重点在于如何在MVVM各层之间使用RAC的信号来更方便的在各个层之间进行响应式数据交互。 demo需求:一个登录界面(登录界面只有账号和密码都有输入,登录按钮才可以点击操作)࿰…...

图文解析ASN.1中BER编码:结构类型、编码方法、编码实例
本文将详细介绍ASN.1中的BER编码规则,包括其编码机制、数据类型表示、以及如何将复杂的数据结构转换为二进制数据。通过本文的阅读,读者将对ASN.1中的BER编码有一个全面的理解。 目录 一.引言 二.BER编码基本结构 ▐ 1. 类型域(Type&#…...

jQuery如何停止动画队列
在jQuery中,你可以使用.stop()方法来停止动画队列。.stop()方法有几个可选的参数,可以用来控制停止动画的方式。 以下是.stop()方法的基本用法和一些参数选项: 无参数:立即停止当前动画,并跳到最后的状态。后续的动画…...

vue3+electron搭建桌面软件
vue3electron开发桌面软件 最近有个小项目, 客户希望像打开 网易云音乐 那么简单的运行起来系统. 前端用 Vue 会比较快一些, 因此决定使用 electron 结合 Vue3 的方式来完成该项目. 然而, 在实施过程中发现没有完整的博客能够记录从创建到打包的流程, 摸索一番之后, 随即梳理…...

oracle常用经典SQL查询
oracle常用经典SQL查询(转贴) oracle常用经典SQL查询 常用SQL查询: 1、查看表空间的名称及大小 select t.tablespace_name, round(sum(bytes/(1024*1024)),0) ts_size from dba_tablespaces t, dba_data_files d where t.tablespace_name d.tablespace_name grou…...

Android shell 常用 debug 命令
目录 1、查看版本2、am 命令3、pm 命令4、dumpsys 命令5、sed命令6、log定位查看APK进程号7、log定位使用场景 1、查看版本 1.1、Android串口终端执行 getprop ro.build.version.release #获取Android版本 uname -a #查看linux内核版本信息 uname -r #单独查看内核版本 1.2、…...

Unity3D Shader数据传递语法详解
在Unity3D中,Shader是用于渲染图形的一种程序,它定义了物体在屏幕上的外观。Shader通过接收输入数据(如顶点位置、纹理坐标、光照信息等)并计算像素颜色来工作。为了使得Shader能够正确运行并产生期望的视觉效果,我们需…...

计算机组成原理(五)
一、链式查询方式 接口的优先级固定不变 在链式查询的情况下,设备的优先级通常与其在链中的位置有关。具体来说,越靠近查询链的起始位置的设备通常具有较高的优先级,而越靠近链的末尾位置的设备优先级较低。 优点: 简单实现&am…...
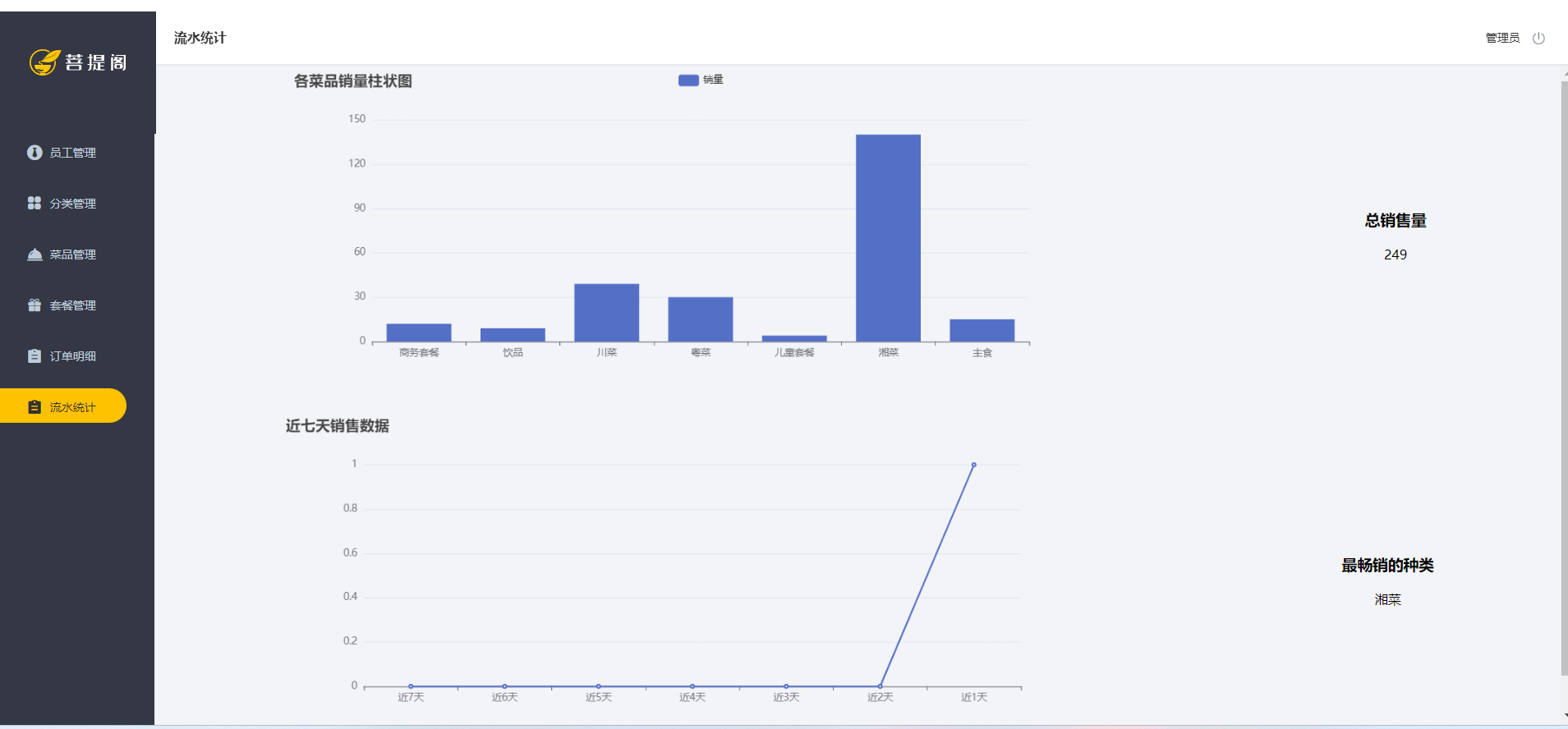
后端项目实战--瑞吉外卖项目软件说明书
瑞吉外卖项目软件说明书 一、项目概述 瑞吉外卖项目是一个外卖服务平台,用户可以通过该平台浏览餐厅菜单、下单、支付以及追踪订单状态。产品原型就是一款产品成型之前的一个简单的框架,就是将页面的排版布局展现出来,使产品得初步构思有一…...
LeetCode | 27.移除元素
这道题的思路和26题一模一样,由于要在元素组中修改,我们可以设置一个index表示目前要修改原数组的第几位,由于遍历,访问原数组永远会在我们修改数组之前,所以不用担心数据丢失的问题,一次遍历数组ÿ…...

为什么要选择AWS?AWS的优势有哪些?
亚马逊云服务器(Amazon Web Services,AWS)是全球领先的云计算服务提供商之一,其提供的云服务器是在全球范围内可用的弹性计算服务。对于很多用户来说,他们可能会担心亚马逊云服务器是否会对服务器的使用进行限制。以下…...

【Intel CVPR 2024】通过图像扩散模型生成高质量360度场景,只需要一个语言模型
在当前人工智能取得突破性进展的时代,从单一输入图像生成全景场景仍是一项关键挑战。大多数现有方法都使用基于扩散的迭代或同步多视角内绘。然而,由于缺乏全局场景布局先验,导致输出结果存在重复对象(如卧室中的多张床࿰…...

postman教程-21-Newman运行集合生成测试报告
上一小节我们Postman Newman的安装方法,本小节我们讲解一下Postman Newman的具体使用方法。 使用Newman运行集合 1、导出Postman集合: 在Postman中,选择你想要运行的集合,然后点击“导出”按钮,选择导出为“Collect…...
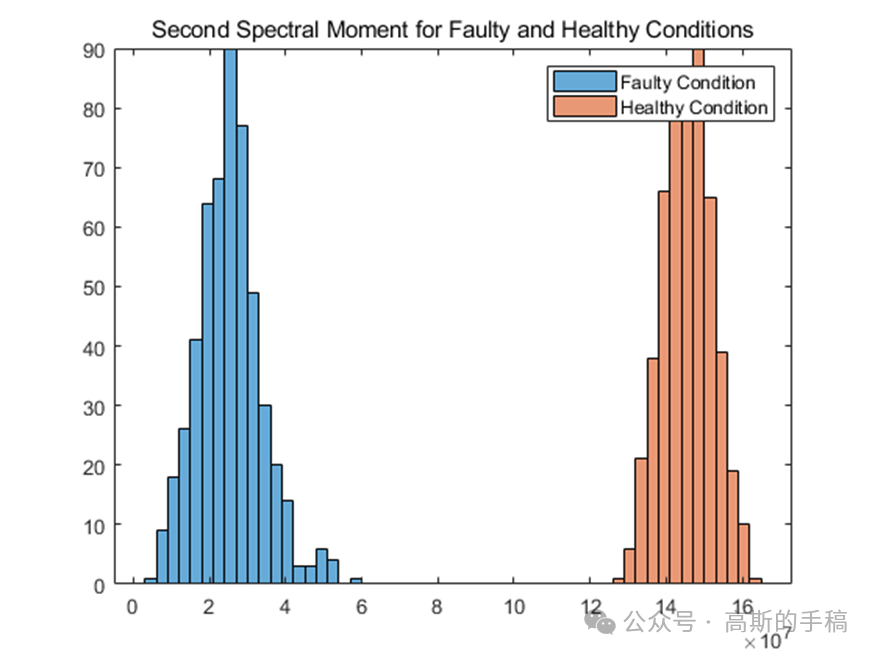
基于条件谱矩的时间序列分析(以轴承故障诊断为例,MATLAB)
谱矩方法可以对数据的表面形貌做较为细致的描述.它以随机过程为理论基础,用各阶谱矩及统计不变量等具体的参数表征表面的几何形态,算术平均顶点曲率是一种基于四阶谱矩的统计不变量。 鉴于此,采用条件谱矩方法对滚动轴承进行故障诊…...

ArcGIS Pro 3.0加载在线高德地图
1、打开ArcGIS Online官网,登录自己的账号,登录后效果如下图所示 官网地址:https://www.arcgis.com/home/webmap/viewer.html 2、点击Add,选择Add Layer from Web,如下图所示 3、在显示的Add Layer from Web页面内&am…...

服务器防漏扫,主机加固方案来解决
什么是漏扫? 漏扫是漏洞扫描的简称。漏洞扫描是一种安全测试方法,用于发现计算机系统、网络或应用程序中的潜在漏洞和安全弱点。通过使用自动化工具或软件,漏洞扫描可以检测系统中存在的已知漏洞,并提供相关的报告和建议…...

Linux2(基本命令2)
目录 一、文件类型分类 二、基本命令 1. find 帮助查询 2. stat 查看文件的信息 3. wc 统计文本 4. 查看文本内容 4.1 cat 4.2 more 4.3 less 4.4 head 4.5 tail 5. cal 显示日历 6. date 显示时间 7. du 文件大小 8. ln 链接 软链接 硬链接 区别 9. history…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
