2024/06/13--代码随想录算法2/17| 62.不同路径、63. 不同路径 II、343. 整数拆分 (可跳过)、96.不同的二叉搜索树 (可跳过)
62.不同路径
力扣链接

动态规划5步曲
- 确定dp数组(dp table)以及下标的含义: dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式,dp[i][j] = dp[i - 1][j] + dp[i][j - 1] i>0,j>0
- dp数组如何初始化
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序【dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。】
- 举例推导dp数组
时间复杂度:O(m × n) 空间复杂度:O(m × n)
class Solution:def uniquePaths(self, m: int, n: int) -> int:dp = [[0]*n for _ in range(m)] ## 创建一个二维列表用于存储唯一路径数# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i-1][j]+dp[i][j-1]# 返回右下角单元格的唯一路径数return dp[m-1][n-1]递归法
class Solution:def uniquePaths(self, m: int, n: int) -> int:if m == 1 or n == 1:return 1return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)63. 不同路径 II
力扣链接
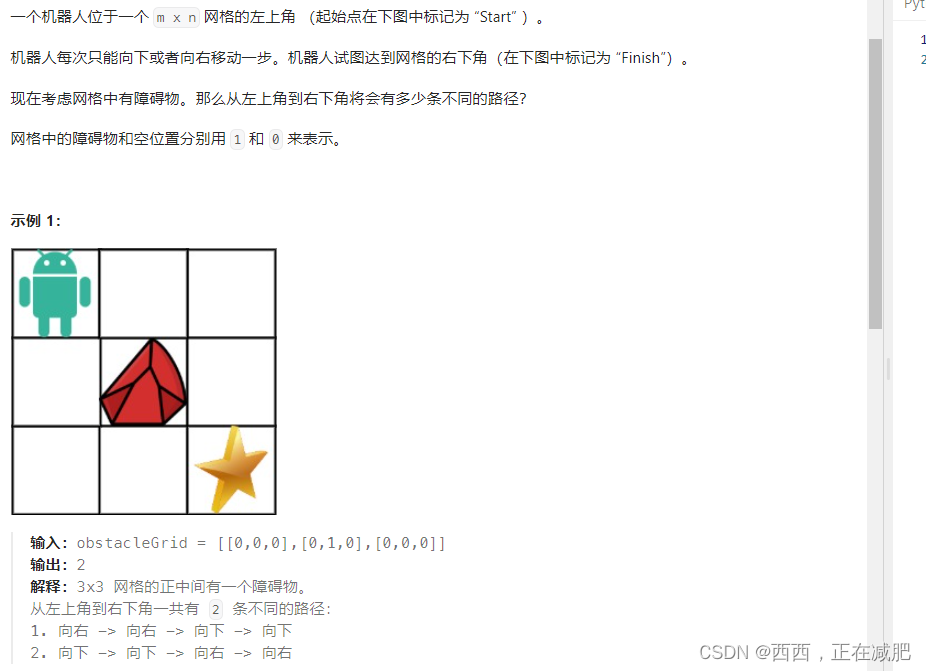
动态规划5步曲
- 确定dp数组(dp table)以及下标的含义:dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式,dp[i][j] = dp[i - 1][j] + dp[i][j - 1] i>0,j>0
- dp数组如何初始化 【但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。】
- 确定遍历顺序【dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。】
- 举例推导dp数组
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid) #行数n = len(obstacleGrid[0]) #列数if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:return 0dp = [[0]*n for _ in range(m)]for i in range(m):if obstacleGrid[i][0] == 0: # 遇到障碍物时,直接退出循环,后面默认都是0dp[i][0] = 1 else:breakfor j in range(n):if obstacleGrid[0][j] == 0:dp[0][j] = 1else:breakfor i in range(1, m):for j in range(1,n):if obstacleGrid[i][j] == 1:continuedp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]
343. 整数拆分 (可跳过)
力扣链接

动态规划5步曲
- 确定dp数组(dp table)以及下标的含义: dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
- 确定递推公式,
可以想 dp[i]最大乘积是怎么得到的呢?【拆成2个,拆成3个以上】
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
j从1开始遍历,dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));- dp数组如何初始化 【dp[2]=1 】
- 确定遍历顺序【从前往后遍历】
- 举例推导dp数组【1<=j <=i-2】
时间复杂度:O(n^2) 空间复杂度:O(n)
class Solution:# 假设对正整数 i 拆分出的第一个正整数是 j(1 <= j < i),则有以下两种方案:# 1) 将 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是 j * (i-j)# 2) 将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是 j * dp[i-j]def integerBreak(self, n):dp = [0] * (n + 1) # #dp[n]: n拆分的整数的乘积的最大值. dp[2] = 1 # 初始化dp[2]为1,因为当n=2时,只有一个切割方式1+1=2,乘积为1# 从3开始计算,直到nfor i in range(3, n + 1):# 遍历所有可能的切割点for j in range(1, i // 2 + 1):# 计算切割点j和剩余部分(i-j)的乘积,并与之前的结果进行比较取较大值dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)return dp[n] # 返回最终的计算结果
96.不同的二叉搜索树 (可跳过)
力扣链接
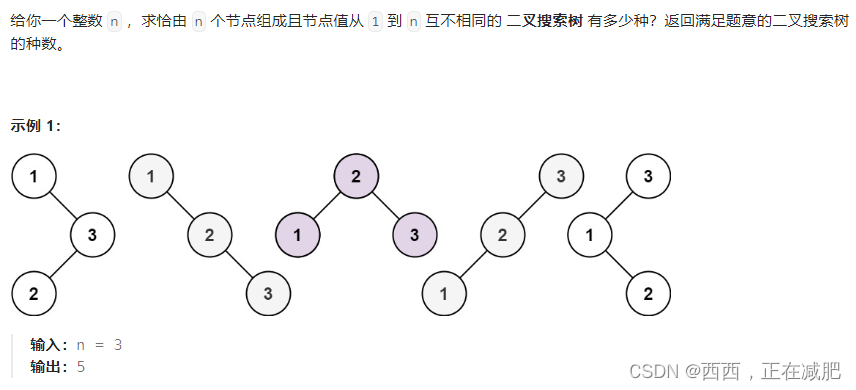

动态规划5步曲
- 确定dp数组(dp table)以及下标的含义: dp[n]:n个节点,组成的二叉树种类。
- 确定递推公式,dp[n] = dp[n-1]*dp[0]+dp[n-2]*dp[1]+dp[n-3]*dp[2]+…+dp[0]*dp[n-1]
- dp数组如何初始化 【dp[0]=1 】
- 确定遍历顺序【那么遍历i里面每一个数作为头结点的状态,用j来遍历】
- 举例推导dp数组
时间复杂度:$O(n^2)$ 空间复杂度:$O(n)$
class Solution:def numTrees(self, n: int) -> int:dp = [0] * (n+1) #dp[n]表示由n个节点组成的二叉搜索树的种类dp[0] = 1 # 当n为0时,只有一种情况,即空树,所以dp[0] = 1for i in range(1,n+1): # 遍历从1到n的每个数字for j in range(0, i): # 对于每个数字i,计算以i为根节点的二叉搜索树的数量dp[i] += dp[j]*dp[i-j-1] # 利用动态规划的思想,累加左子树和右子树的组合数量return dp[n]
相关文章:

2024/06/13--代码随想录算法2/17| 62.不同路径、63. 不同路径 II、343. 整数拆分 (可跳过)、96.不同的二叉搜索树 (可跳过)
62.不同路径 力扣链接 动态规划5步曲 确定dp数组(dp table)以及下标的含义: dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。确定递推公式,dp[i][j] d…...
Android低代码开发 - 直接创建一个下拉刷新列表界面
看了我Android低代码开发 - 让IDE帮你写代码这篇文章的小伙伴,大概都对Dora全家桶开发框架有基本的认识了吧。本篇文章将会讲解如何使用dora-studio-plugin快捷创建一个下拉刷新列表界面。 效果演示 这样直接通过图形界面的方式就创建好了下拉刷新上拉加载空态界面…...

23.Dropout
在深度学习的训练过程中,过拟合是一个常见的问题。为了解决这个问题,研究者们提出了多种正则化技术,其中Dropout技术因其简单而有效的特点,得到了广泛的应用。本文将对Dropout技术的工作原理、主要优点、潜在缺点以及应用场景进行…...

电脑撤回的快捷键是什么?
下面给大家介绍了各种办公应用的撤回以及反向撤回快捷键介绍,在ps、excel中都是可以使用的。 撤回键是ctrl加什么 1、撤销的快捷键是“CtrlZ”,用于取消上一步操作,对与在电脑系统上或软件内的操作均适用。重复按下可以取消多步操作。 2、而…...
每日一题——Python实现PAT甲级1116 Come on! Let‘s C(举一反三+思想解读+逐步优化)五千字好文
一个认为一切根源都是“自己不够强”的INTJ 个人主页:用哲学编程-CSDN博客专栏:每日一题——举一反三Python编程学习Python内置函数 Python-3.12.0文档解读 目录 我的写法 代码点评 时间复杂度分析 空间复杂度分析 总结 我要更强 优化思路 优化…...
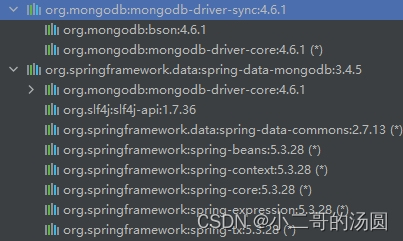
spring-data-mongodb版本兼容问题
spring-data-mongodb与mongodb驱动有兼容性问题,不匹配会报NoSuchMethod异常,mongodb的java驱动包在4.0之后由mongodb-java-driver更名为mongodb-driver-sync。 spring-data-mongodb包依赖中有mongodb-driver-core,但缺诸如MongoCollection等…...

Java的核心类库
引言 在Java编程中,熟练掌握常用类与对象操作是开发的基础。Java的核心类库提供了丰富的功能,可以帮助开发者高效地处理各种编程任务。本文将详细介绍Java字符串操作、集合框架、日期与时间处理等内容,并通过图表和表格进行总结与示范。 字符…...
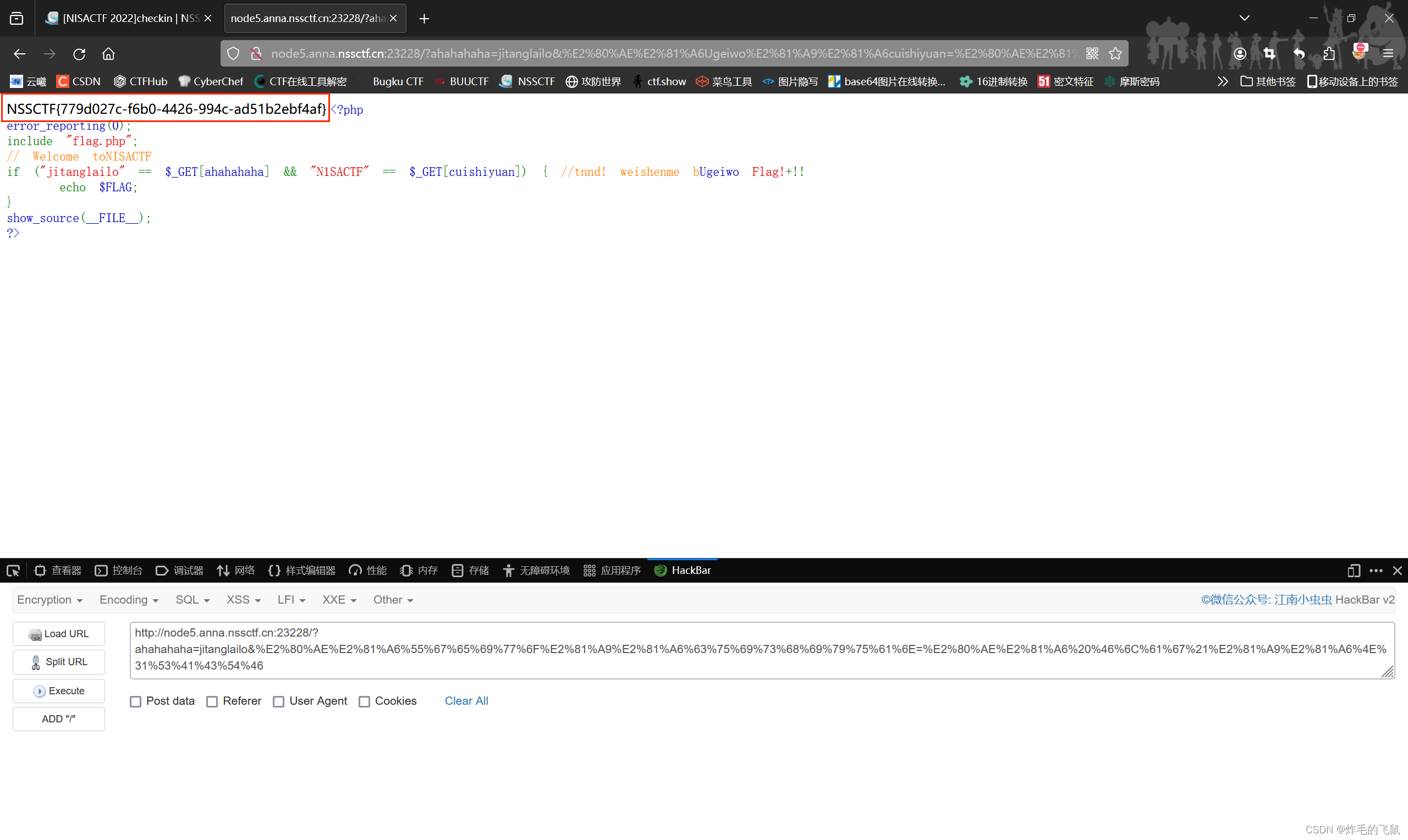
NSS题目练习9
[极客大挑战 2020]welcome 界面打开后一片空白,查看题目描述,翻译过来是 1.除了GET请求方法,还有一种常见的请求方法… 2.学习一些关于sha1和array的知识。 3.更仔细地检查phpinfo,你会发现标志在哪里。 补充: sh…...

JS 【算法】二分查找
使用场景 在有序数组中查找目标元素 const arr [1, 2, 3, 4, 5, 6, 7, 8, 9] const target 2 console.log(binarySearch1(arr, target)) console.log(binarySearch2(arr, target))循环实现 function binarySearch1(arr, target) {const length arr.lengthif (length 0) re…...
—— Webpack(v5.91.0):应用模块打包器与构建工具)
前端工程化工具系列(十四)—— Webpack(v5.91.0):应用模块打包器与构建工具
Webpack 是用于现代 JavaScript 应用程序的静态模块打包器。 当 webpack 处理应用程序时,它会在内部构建一个依赖关系图,该图映射项目所需的每个模块最终会生成一个或多个包。 1 概念 1.1 modules Webpack 中,无论是 JS 、CSS 还是图片等&…...
ThinkPHP+Bootstrap简约自适应网址导航网站源码
使用 ThinkPHPbootstrap 开发,后台采用全局 ajax 无刷新加载,前后台自适应,前台页面非常简洁适合自己收藏网站或做导航网站。 搭建教程: 1.整个主机 2.绑定解析域名 3.上传源码,解压 把解压出来的 nav.sql 文件导入数…...
Flutter 使用ffigen生成ffmpeg的dart接口
Flutter视频渲染系列 第一章 Android使用Texture渲染视频 第二章 Windows使用Texture渲染视频 第三章 Linux使用Texture渲染视频 第四章 全平台FFICustomPainter渲染视频 第五章 Windows使用Native窗口渲染视频 第六章 桌面端使用texture_rgba_renderer渲染视频 第七章 使用ff…...
: No CUDA toolset found.)
(message): No CUDA toolset found.
解决方法: C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.2\extras\visual_studio_integration\MSBuildExtensions\ 下的4个文件 复制到 D:\Program Files\Microsoft Visual Studio\2022\Enterprise\MSBuild\Microsoft\VC\v170\BuildCustomizations\下。…...

【python】邮箱正则验证
当然可以。以下是一个使用Python正则表达式的例子,用于检查一个字符串是否是一个有效的电子邮件地址: import re def is_valid_email(email):regex r^[a-zA-Z0-9._%-][a-zA-Z0-9.-]\.[a-zA-Z]{2,}$return bool(re.match(regex, email)) # 测试电子邮件…...

深度学习(四)——torchvision中数据集的使用
1. 参数详解 torchvision中每个数据集的参数都是大同小异的,这里只介绍CIFAR10数据集 该数据集的数据格式为PIL格式 class torchvision.datasets.CIFAR10(root:str,train:boolTrue,transform:Optional[Callable]None,target_transform:Optional[Callable]None,do…...

【全开源】图书借阅管理系统源码(ThinkPHP+FastAdmin)
📚图书借阅管理系统:打造你的私人图书馆 一款基于ThinkPHPFastAdmin开发的简易图书借阅管理系统,一款轻量级的图书借阅管理系统,具有会员管理,图书管理,借阅及归还管理,会员充值等基本功能&…...
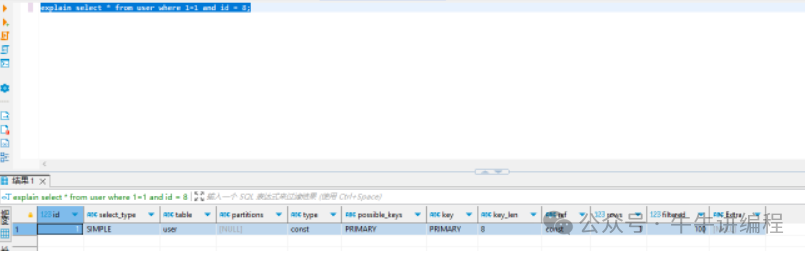
Mysql中使用where 1=1有什么问题吗
昨天偶然看见一篇文章,提到说如果在mysql查询语句中,使用where 11会有性能问题?? 这着实把我吸引了,因为我项目中就有不少同事,包括我自己也有这样写的。为了不给其他人挖坑,赶紧学习一下&…...
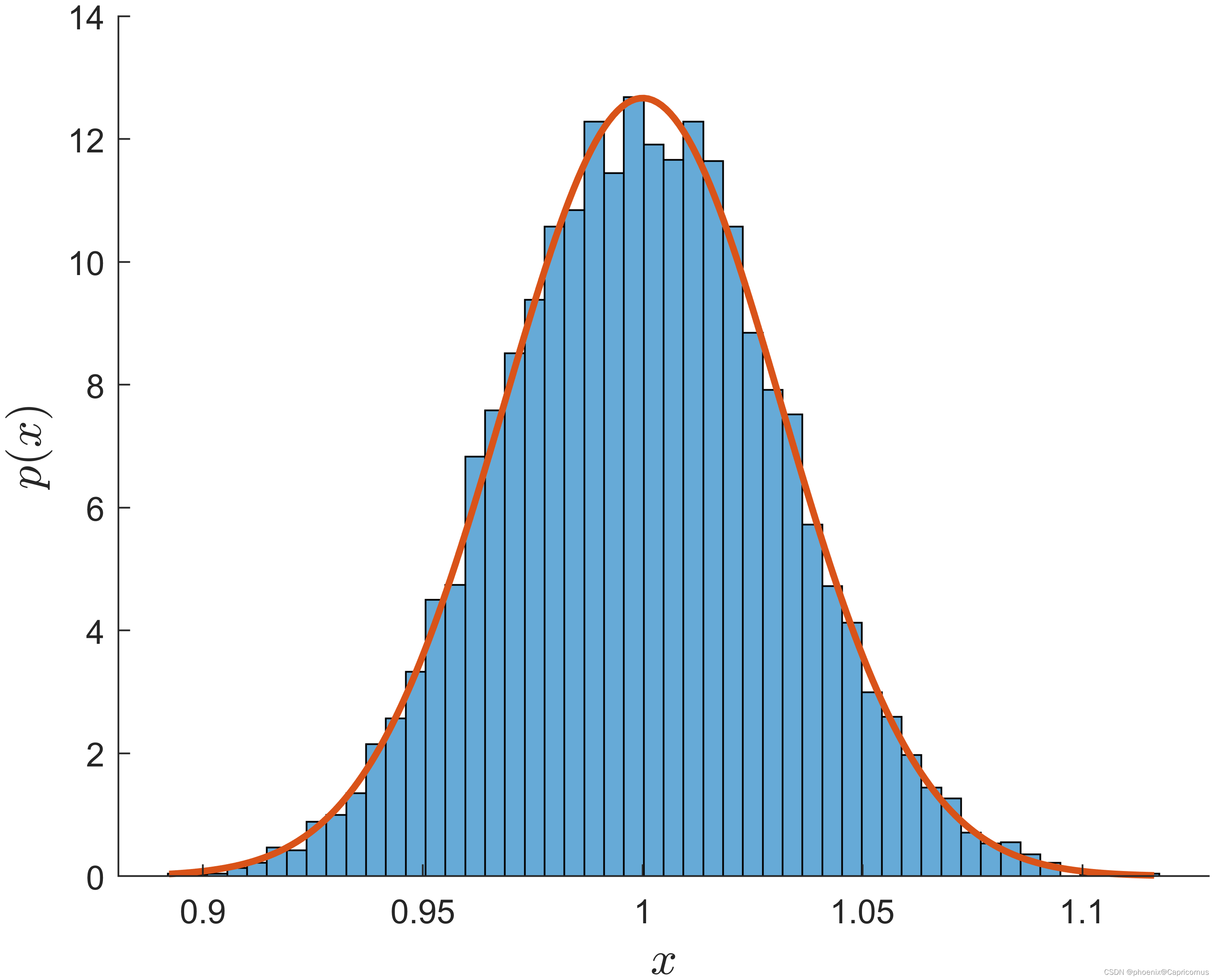
中心极限定理的MATLAB例
独立同分布的中心极限定理: 设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是独立同分布的随机变量序列,且 E ( X i ) μ E(X_i) \mu E(Xi)μ, D ( X i ) σ 2 > 0 D(X_i) \sigma^2 > 0 D(Xi)σ2>0&a…...

定义input_password函数,提示用户输入密码.如果用户输入长度<8,抛出异常,如果用户输入长度>=8,返回输入的密码
def input_password(password):str1passwordlen1len(str1)try:if len1<8:raise ValueError("密码长度不能小于8")else:return print(f"你的密码为:{password},请确认")except ValueError as e:print(f":Error is {e}")number1input("请…...

【深度学习】IP-Adapter 和 InstantID 的核心机制比较
IP-Adapter 和 InstantID 是两个在图像生成中具有不同优势和应用场景的模型。以下是这两个模型的区别及其理论分析。 IP-Adapter 特点: 图像提示能力: IP-Adapter 通过引入图像提示能力,使得预训练的文本到图像扩散模型可以接受图像作为提示,从而生成…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
