机器学习--回归模型和分类模型常用损失函数总结(详细)

文章目录
- 引言
- 回归模型常用损失函数
- 均方误差(Mean Squared Error, MSE)
- 均方根误差(Root Mean Squared Error, RMSE)
- 平均绝对误差(Mean Absolute Error, MAE)
- Huber损失(Huber Loss)
- 分类模型常用损失函数
- 交叉熵损失(Cross-Entropy Loss)
- Hinge损失(Hinge Loss)
- Kullback-Leibler散度(Kullback-Leibler Divergence, KL散度)
- 总结
- 回归模型
- 分类模型
引言
在机器学习和统计学领域,损失函数是评估和优化模型性能的核心工具。它们通过量化模型预测值与真实值之间的差异,指导模型的训练过程,最终影响模型的准确性和可靠性。不同类型的损失函数适用于不同的任务,如回归问题和分类问题,因此选择合适的损失函数是构建高效模型的关键步骤。
在回归问题中,常见的损失函数包括均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)和Huber损失。每种损失函数都有其独特的优缺点和适用场景,例如,MSE在处理大误差时表现良好,但对异常值敏感;MAE对异常值更鲁棒,但梯度不连续。Huber损失则结合了MSE和MAE的优点,在面对异常值时表现出较好的鲁棒性。
对于分类问题,交叉熵损失是最常用的损失函数,广泛应用于二分类和多分类任务,特别是在深度学习中。它通过优化预测概率分布,帮助模型在复杂任务中取得优异的表现。其他常用的损失函数如Hinge损失和Kullback-Leibler散度(KL散度),分别在支持向量机和概率模型中有着重要应用。
本文将深入探讨回归模型和分类模型中常用的损失函数,分析它们的数学公式、优缺点以及适用场景,帮助读者更好地理解和选择合适的损失函数来优化机器学习模型。
回归模型常用损失函数
均方误差(Mean Squared Error, MSE)
MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
优点:
平滑性:误差平方使得损失函数平滑且容易求导,有助于梯度下降法等优化算法。
放大大误差:平方项会放大大误差的影响,使模型更关注大误差。
缺点:
对异常值敏感:因为误差被平方,大的异常值会极大地增加损失值,影响模型的鲁棒性。
适用场景: 当数据中异常值较少且对大误差的敏感度要求高时使用。
均方根误差(Root Mean Squared Error, RMSE)
RMSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} RMSE=n1∑i=1n(yi−y^i)2
优点:
直观性:与MSE相比,RMSE保留了平方误差放大大误差的特性,但单位与原始数据相同,更容易解释。
缺点:
计算复杂度:相比MSE多了一步平方根计算。
适用场景:
同MSE,且需要损失函数值与数据原始单位一致时。
平均绝对误差(Mean Absolute Error, MAE)
MAE = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| MAE=n1∑i=1n∣yi−y^i∣
优点:
鲁棒性:对异常值不敏感,因为误差没有被平方。
易解释:损失值直接反映平均预测误差的大小。
缺点:
梯度不连续:在误差为零点处,梯度不连续,可能导致优化算法收敛较慢。
适用场景:
数据中含有异常值且需要对这些异常值有更高容忍度时。
Huber损失(Huber Loss)
Huber ( y , y ^ ) = { 1 2 ( y − y ^ ) 2 if ∣ y − y ^ ∣ ≤ δ δ ∣ y − y ^ ∣ − 1 2 δ 2 if ∣ y − y ^ ∣ > δ \text{Huber}(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{if } |y - \hat{y}| \leq \delta \\ \delta |y - \hat{y}| - \frac{1}{2}\delta^2 & \text{if } |y - \hat{y}| > \delta \end{cases} Huber(y,y^)={21(y−y^)2δ∣y−y^∣−21δ2if ∣y−y^∣≤δif ∣y−y^∣>δ
优点:
平衡性:结合了MSE和MAE的优点,小误差时类似于MSE,大误差时类似于MAE,对异常值有一定的鲁棒性。
可调参数:参数 ( δ ) (\delta) (δ) 可以根据具体情况调整,灵活性强。
缺点:
参数调整:需要调整参数 ( δ ) (\delta) (δ),不适当的 ( δ ) (\delta) (δ)值可能影响模型性能。
适用场景:
当数据中存在少量异常值且需要模型对大误差和小误差都能进行有效处理时。
分类模型常用损失函数
交叉熵损失(Cross-Entropy Loss)
二分类交叉熵损失:
Binary Cross-Entropy = − 1 n ∑ i = 1 n [ y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ] \text{Binary Cross-Entropy} = - \frac{1}{n} \sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] Binary Cross-Entropy=−n1∑i=1n[yilog(y^i)+(1−yi)log(1−y^i)]
多分类交叉熵损失:
Categorical Cross-Entropy = − 1 n ∑ i = 1 n ∑ c = 1 C y i , c log ( y ^ i , c ) \text{Categorical Cross-Entropy} = - \frac{1}{n} \sum_{i=1}^{n} \sum_{c=1}^{C} y_{i,c} \log(\hat{y}_{i,c}) Categorical Cross-Entropy=−n1∑i=1n∑c=1Cyi,clog(y^i,c)
优点:
适用性广:广泛应用于分类问题,特别是深度学习模型。
概率解释:损失函数值与概率相关,直观且易于理解。
良好梯度特性:对概率预测进行优化效果好。
缺点:
对错误分类惩罚较高:可能导致模型在异常数据上过拟合。
适用场景:
二分类和多分类任务,如图像分类、文本分类等。
Hinge损失(Hinge Loss)
Hinge Loss = 1 n ∑ i = 1 n max ( 0 , 1 − y i y ^ i ) \text{Hinge Loss} = \frac{1}{n} \sum_{i=1}^{n} \max(0, 1 - y_i \hat{y}_i) Hinge Loss=n1∑i=1nmax(0,1−yiy^i)
其中, ( y i ) ( y_i ) (yi) 为真实标签(取值为+1或-1), ( y ^ i ) (\hat{y}_i) (y^i) 为预测值。
优点:
分类边界优化:对分类边界的优化效果好,适用于支持向量机(SVM)。
对大间隔分类器友好:鼓励模型找到更大的分类间隔。
缺点:
仅适用于线性可分问题:对非线性可分问题效果不佳。
不处理概率输出:不能直接用于概率模型。
适用场景:
线性可分问题和支持向量机的应用场景。
Kullback-Leibler散度(Kullback-Leibler Divergence, KL散度)
KL ( P ∥ Q ) = ∑ i = 1 n P ( i ) log P ( i ) Q ( i ) \text{KL}(P \| Q) = \sum_{i=1}^{n} P(i) \log \frac{P(i)}{Q(i)} KL(P∥Q)=∑i=1nP(i)logQ(i)P(i)
其中, ( P ) (P) (P) 和 ( Q ) (Q) (Q) 是两个概率分布。
优点:
测量概率分布差异:适用于比较两个概率分布,特别是处理概率模型的输出。
灵活性:适用于多种任务中的概率分布比较。
缺点:
计算不稳定性:当 ( Q ( i ) ) (Q(i)) (Q(i)) 很小或为零时,计算结果会不稳定。
不对称性: ( KL ( P ∥ Q ) ≠ KL ( Q ∥ P ) ) (\text{KL}(P \| Q) \neq \text{KL}(Q \| P)) (KL(P∥Q)=KL(Q∥P)),需要注意使用场景。
适用场景:
处理概率分布差异的任务,如语言模型、生成对抗网络(GAN)等。
总结
回归模型
**均方误差(MSE)**适用于大多数回归问题,特别是异常值较少的情况下。
**均方根误差(RMSE)**适用于需要损失函数值与原始数据单位一致的场景。
**平均绝对误差(MAE)**适用于对异常值敏感度要求低的场景。
Huber损失适用于数据中存在少量异常值且需要综合处理大误差和小误差的场景。
分类模型
交叉熵损失广泛适用于二分类和多分类任务,特别是在深度学习中。
Hinge损失适用于线性可分问题和支持向量机应用。
KL散度适用于需要比较概率分布的任务,如语言模型和生成对抗网络。
选择合适的损失函数不仅取决于具体的任务和数据特性,还需要考虑模型的优化难度、对异常值的处理能力以及应用场景的具体要求。
相关文章:

机器学习--回归模型和分类模型常用损失函数总结(详细)
文章目录 引言 回归模型常用损失函数均方误差(Mean Squared Error, MSE)均方根误差(Root Mean Squared Error, RMSE)平均绝对误差(Mean Absolute Error, MAE)Huber损失(Huber Loss) …...

企业选择数字工厂管理系统供应商的标准是什么
随着信息技术的飞速发展,数字化转型已成为企业提升竞争力、实现可持续发展的必由之路。在制造业领域,数字工厂管理系统实现生产流程自动化、智能化的关键工具,其选择的重要性不言而喻。本文将从多个维度探讨企业选择数字工厂管理系统供应商的…...

京准电钟|基于纳秒级的GPS北斗卫星授时服务器
京准电钟|基于纳秒级的GPS北斗卫星授时服务器 京准电钟|基于纳秒级的GPS北斗卫星授时服务器 你有没有思考过这样一个问题:火车站内,熙熙攘攘,旅客排队进站、列车停靠发车,一切井然有序。一旦有个别时间出现…...

Flutter知识点
Dart语言基础知识 Dart特性: Dart 是少数同时支持 JIT(Just In Time,即时编译)和 AOT(Ahead of Time,运行前编译)的语言之一。语言在运行之前通常都需要编译,JIT 和 AOT 则是最常见…...

2024-06-12 问AI: 在大语言模型中,什么是Jailbreak漏洞?
文心一言 在大语言模型中,Jailbreak漏洞(也称为越狱攻击或指令注入攻击)是一种特定的安全漏洞,它允许用户或攻击者通过精心设计的输入或指令,绕过模型的安全限制,诱导模型产生原本被设定为禁止或限制的输出…...

Vue22-v-model收集表单数据
一、效果图 二、代码 2-1、HTML代码 2-2、vue代码 1、v-model单选框的收集信息 v-model:默认收集的就是元素中的value值。 单选框添加默认值: 2、v-model多选框的收集信息 ①、多个选择的多选 注意: 此处的hobby要是数组!&…...

【深度学习】深入解码:提升NLP生成文本的策略与参数详解
文章目录 解码策略解码参数公式解释代码例子区别 更详细的束搜索的解释更详细的例子解释第一步第二步第三步 解码策略和解码参数在自然语言处理(NLP)模型的生成过程中起着不同的作用,但它们共同决定了生成文本的质量和特性。 解码策略 解码…...
Petalinux由于网络原因产生的编译错误(2)--Fetcher failure:Unable to find file
1 Fetcher failure:Unable to find file 错误 如果编译工程遇到如下图所示的“Fetcher failure for URL”或相似错误 出现这种错误的原因是 Petalinux 在配置和编译的时候,需要联网下载一些文件,由于网 络原因这些文件不能正常下载,导致编译…...
随手记:商品信息过多,展开收起功能
UI原型图: 页面思路: 在商品信息最小item外面有一个包裹所有item的标签,控制这个标签的高度来实现展开收起功能 <!-- 药品信息 --><view class"drugs" v-if"inquiryInfoSubmitBtn"><view class"…...
uniapp上传头像并裁剪图片
第一步写上uniapp自带的选择图片button按钮 点击之后会弹出选择图片的方式 拍照或从相册选择图片后将会跳到图片裁剪 然后我们裁剪完之后点击确定在上传图片 这里是上传图片的接口 拿到本地图片 上传的话自己想以那种方式上传都可以...

9.1.3 简单介绍单阶段模型YOLO、YOLOv2、YOLO9000、YOLOv3的发展过程
9.1.3 简单介绍单阶段模型YOLO、YOLOv2、YOLO9000、YOLOv3的发展过程 前情回顾:9.1.2 简单介绍两阶段模型R-CNN、SPPNet、Fast R-CNN、Faster R-CNN的发展过程 摘要 YOLOYOLOv2YOLO9000YOLOv3基本思想使用一个端到端的卷积神经网络直接预测目标的类别和位置针对YOL…...

英智教育智能体,AI Agent赋能教育培训行业数字化升级
教育是当前需求巨大且没有足够人力来满足的领域,每个学生个体差异较大,有限的教师资源无法针对性实行差异教学,学生学不会,教师教学压力大等问题普遍存在。 面对这些难题,英智在通用大模型能力的基础上,整合…...
什么是电脑监控软件?六款知名又实用的电脑监控软件
电脑监控软件是一种专为监控和记录计算机活动而设计的应用程序,它能够帮助用户(如家长、雇主或系统管理员)了解并管理目标计算机的使用情况。这些软件通常具有多样化的功能,包括但不限于屏幕捕捉、网络行为监控、应用程序使用记录…...

小程序名片怎么生成?AI名片生成器源码系统 为企业店铺创建自己的数字名片
在数字化时代,小程序名片已经成为企业店铺展示自身形象、推广产品和服务的重要工具。分享一个AI名片生成器源码系统春哥AI雷达智能名片小程序系统企业商业运营版,含完整代码包和详细的图文安装部署搭建教程,新手也能轻松使用,源码…...

浅谈PMP:项目管理的专业化认证
引言: 项目管理作为现代企业运营的核心环节,其重要性不言而喻。随着全球化的加速和市场竞争的加剧,企业对项目管理的需求日益增长,项目管理专业人员的需求也水涨船高。在这样的背景下,PMP(Project Managem…...

获取闲鱼商品详情api
要使用闲鱼商品详情API,你需要先申请一个开发者账号,并且在开发者中心创建一个应用,目前很难申请到,还有一个方式是获取第三方应用的AppKey和AppSecret直接使用。 API的请求地址为: https://api.m.taobao.com/h5/mto…...
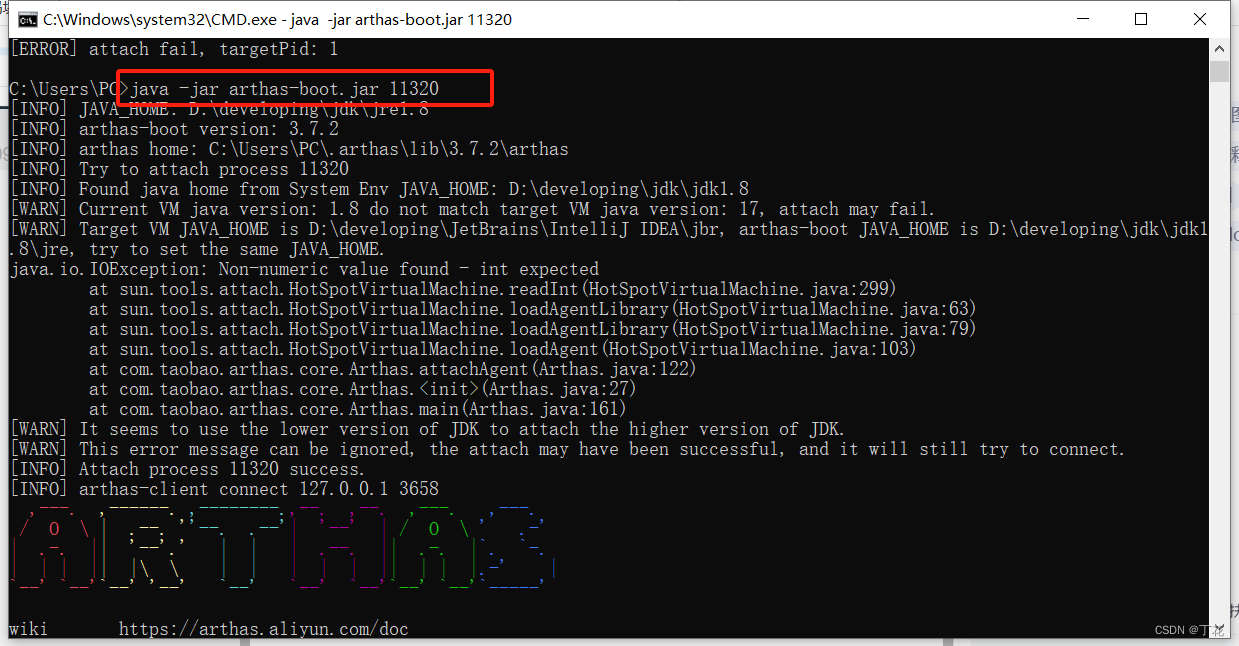
java1.8运行arthas-boot.jar运行报错解决
报错内容 输入java -jar arthas-boot.jar,后报错。 [INFO] JAVA_HOME: D:\developing\jdk\jre1.8 [INFO] arthas-boot version: 3.7.2 [INFO] Can not find java process. Try to run jps command lists the instrumented Java HotSpot VMs on the target system.…...

每日一练 - IGMP协议与查询器选举机制
01 真题题目 在共享网络中存在多台路由器的情况下,是否是IGMP协议本身负责选举出查询器的角色? A. 正确 B. 错误 02 真题答案 B 03 答案解析 IGMP(Internet Group Management Protocol)互联网组管理协议,主要用于IP多…...
)
深入浅出:面向对象软件设计原则(OOD)
目录 前言 1.单一责任原则(SRP) 2.开发封闭原则(OCP) 3.里氏替换原则(LSP) 4.依赖倒置原则(DIP) 5.接口分离原则(ISP) 6.共同封闭原则(CCP)…...

缓存与数据一致性问题
1、更新了数据库,再更新缓存 假设数据库更新成功,缓存更新失败,在缓存失效和过期的时候,读取到的都是老数据缓存。 2、更新缓存,更新数据库 缓存更新成功了,数据库更新失败,是不是读取的缓存的都…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
