6-11 函数题:某范围中的最小值
6-11 函数题:某范围中的最小值
分数 5
全屏浏览
作者 雷丽兰
单位 宜春学院
有n(n<=1000)个整数,从这n个整数中找到值落在(60至100之间)的最小整数。
函数接口定义:
int min ( int arr[], int n);
说明:其中 `arr,n`都是用户传入的参数。 函数返回数组arr中的值落在60至100之间的最小整数。
裁判测试程序样例:
#include <stdio.h>
#define N 1000
int min ( int arr[], int n);int main(){int arr[N];int n;scanf("%d", &n);for(int i=0;i<n;i++){ scanf("%d", &arr[i]); }int m = min(arr,n);if(m==101)printf("NO\n",m );else printf("%d\n",m);return 0;}/* 请在这里填写答案: */输入样例1:
在这里给出一组输入。例如:
5
66 22 95 44 63
输出样例1:
在这里给出相应的输出。例如:
63输入样例2:
在这里给出一组输入。例如:
5
102 22 55 44 33
输出样例2:
在这里给出相应的输出。例如:
NO代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
函数代码分享:
int min ( int arr[], int n){int min=0,flag=0;for(int i=0;i<n;i++){if(arr[i]>=60&&arr[i]<=100&&flag==0){min=arr[i];flag=1;}else if(arr[i]>=60&&arr[i]<=100&&arr[i]<min)min=arr[i];}if(min==0&&flag==0)return 101;elsereturn min;
}相关文章:

6-11 函数题:某范围中的最小值
6-11 函数题:某范围中的最小值 分数 5 全屏浏览 作者 雷丽兰 单位 宜春学院 有n(n<1000)个整数,从这n个整数中找到值落在(60至100之间)的最小整数。 函数接口定义: int min ( int arr[], int n); 说明…...
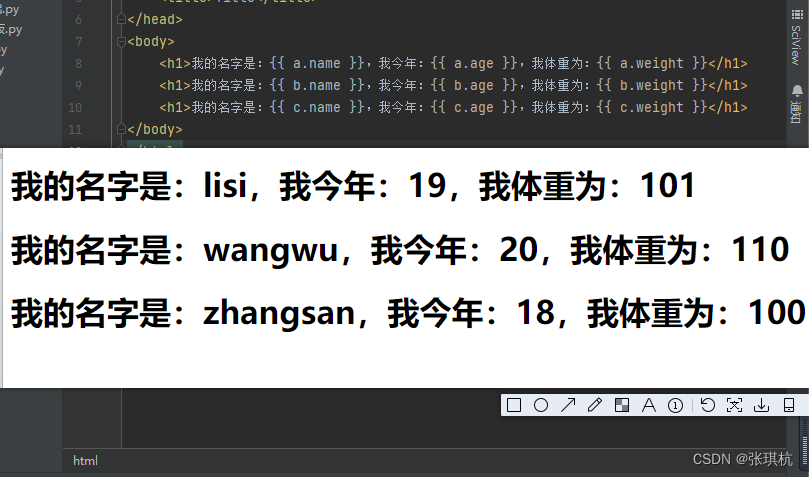
Flask基础2-Jinja2模板
目录 1.介绍 2.模板传参 1.变量传参 2.表达式 3.控制语句 4.过滤器 5.自定义过滤器 6.测试器 7.块和继承 flask基础1 1.介绍 Jinja2:是Python的Web项目中被广泛应用的模板引擎,是由Python实现的模板语言,Jinja2 的作者也是 Flask 的作 者。他的设计思想来源于Django的模…...
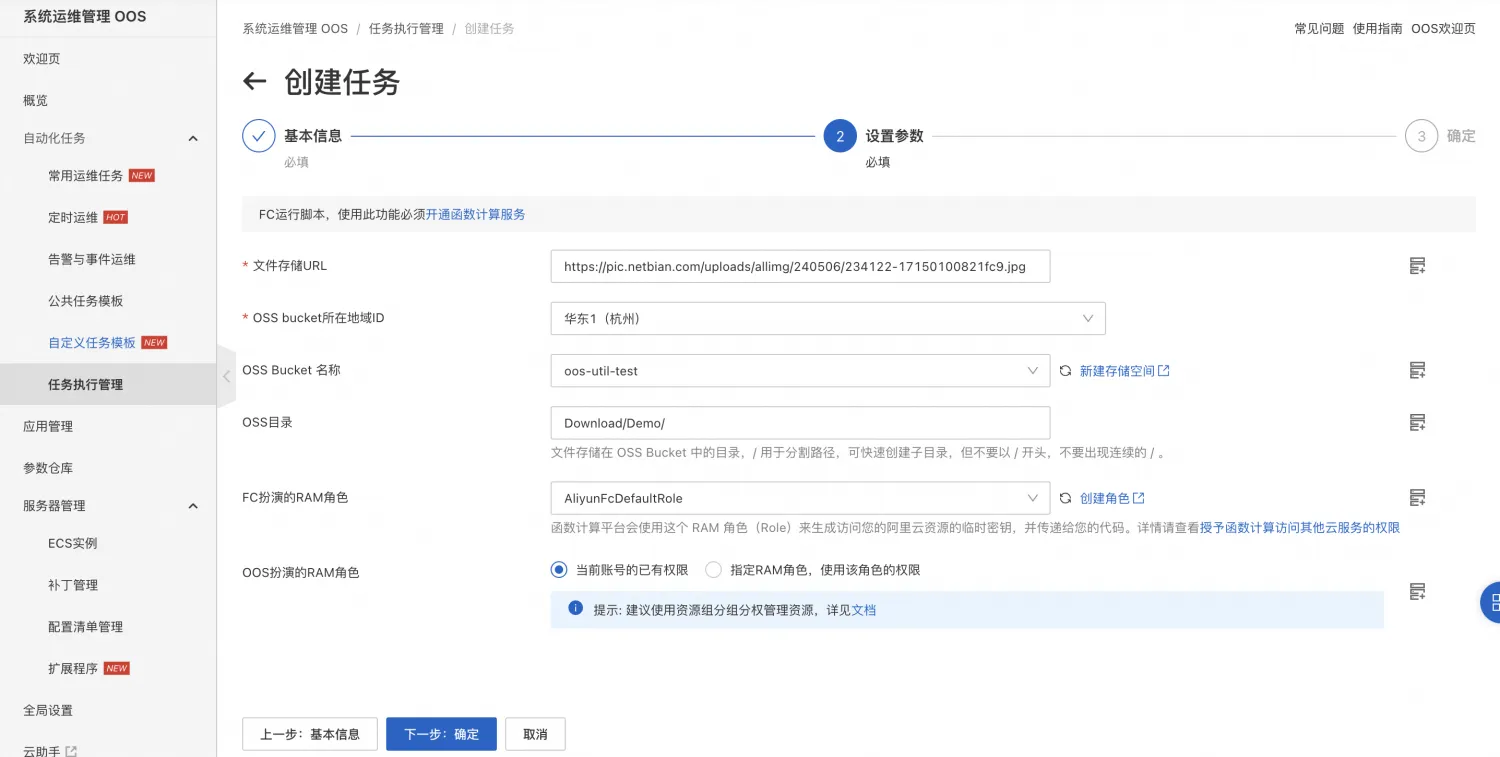
Serverless 使用OOS将http文件转存到对象存储
目录 背景介绍 系统运维管理OOS 文件转存场景 前提条件 实践步骤 附录 示例模板 背景介绍 系统运维管理OOS 系统运维管理OOS(CloudOps Orchestration Service)提供了一个高度灵活和强大的解决方案,通过精巧地编排阿里云提供的OpenAPI…...
AcWing 477:神经网络 ← 拓扑排序+链式前向星
【题目来源】https://www.acwing.com/problem/content/479/【题目描述】 人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。 对神经网络的研究…...

鲁教版八年级数学下册-笔记
文章目录 第六章 特殊平行四边形1 菱形的性质与判定2 矩形的性质与判定3 正方形的性质与判定 第七章 二次根式1 二次根式2 二次根式的性质3 二次根式的加减二次根式的乘除 第八章 一元二次方程1 一元二次方程2 用配方法解一元二次方程3 用公式法解一元二次方程4 用因式分解法解…...

Web前端栅格:深入解析与实战应用
Web前端栅格:深入解析与实战应用 在Web前端开发中,栅格系统是一种重要的布局工具,它能够帮助我们快速构建响应式、灵活且美观的页面布局。然而,对于许多初学者和从业者来说,栅格系统的概念、原理以及实际应用却常常令…...

mysql Innodb引擎常见问题
问题 1:InnoDB 引擎的主要特点有哪些? 答:支持事务、行级锁、外键约束,具有较好的数据完整性和并发性。 问题 2:InnoDB 如何实现事务的 ACID 特性? 答:通过原子性(事务要么全部成功要…...
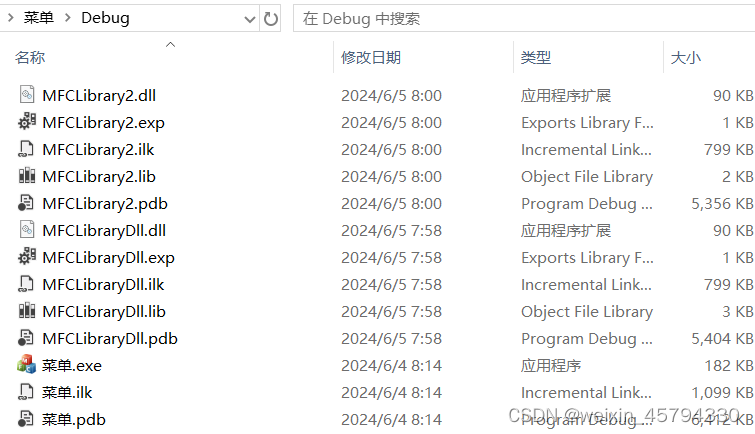
创建 MFC DLL-使用关键字_declspec(dllexport)
本文仅供学习交流,严禁用于商业用途,如本文涉及侵权请及时联系本人将于及时删除 从MFC DLL中导出函数的另一种方法是在定义函数时使用关键字_declspec(dllexport)。这种情况下,不需要DEF文件。 导出函数的形式为: declspec(dll…...
机器学习笔记 - 用于3D数据分类、分割的Point Net的网络实现
上一篇,我们大致了解了Point Net的原理,这里我们要进行一下实现。 机器学习笔记 - 用于3D数据分类、分割的Point Net简述-CSDN博客文章浏览阅读3次。在本文中,我们将了解Point Net,目前,处理图像数据的方法有很多。从传统的计算机视觉方法到使用卷积神经网络到Transforme…...

C#知识|基于实体类对象,返回实体集合封装介绍。
哈喽,你好啊,我是雷工! 前面通过实体类封装传递了零散的参数,打包后给数据访问方法。 但当查询结果是数据集,要把查询到的数据返回给UI时,我们也可以把返回的多条零散数据封装到实体类中。 此次练习可以使用实体容器:泛型集合List<T>,当把每条数据封装成实体对…...
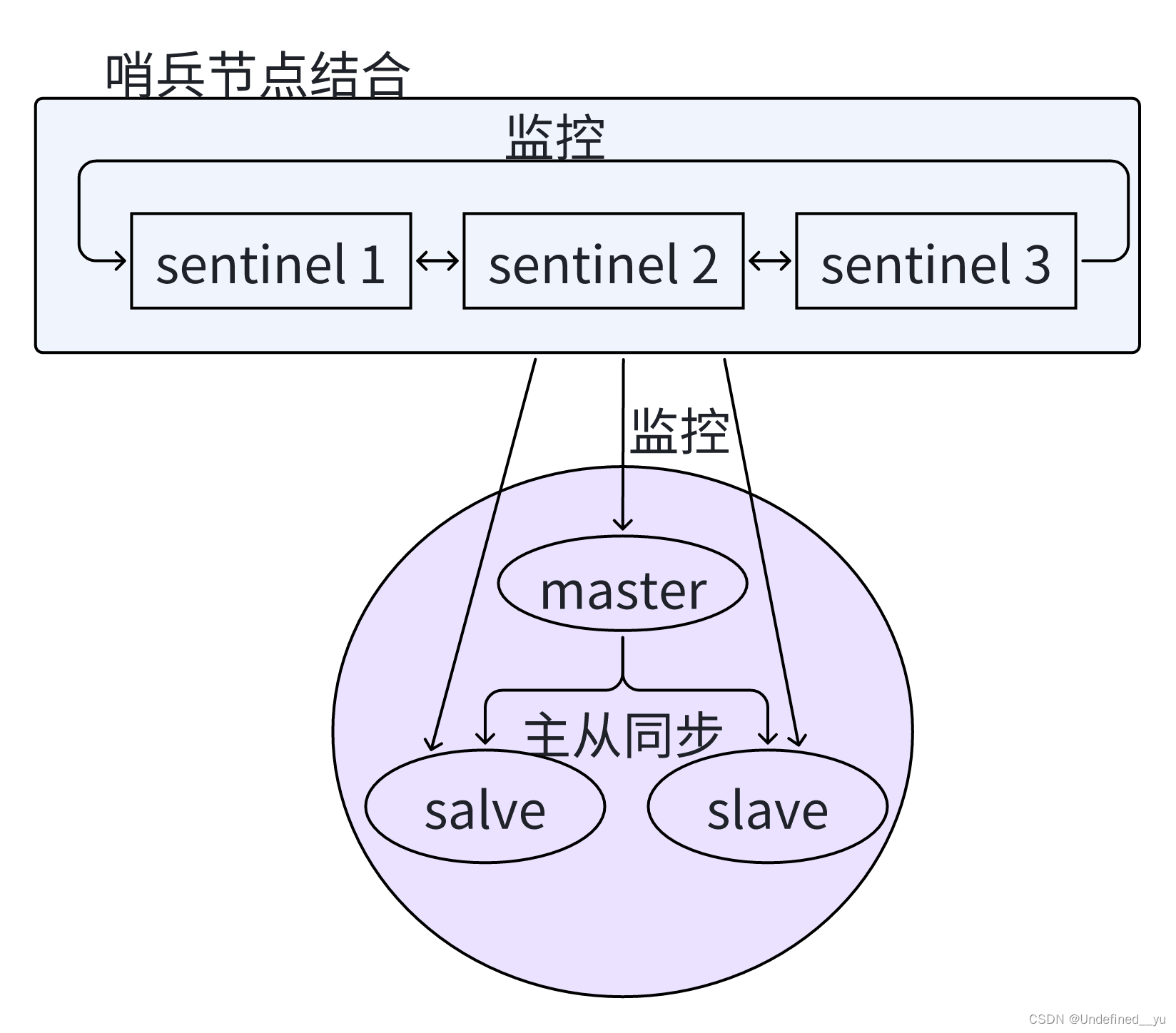
关于Redis中哨兵(Sentinel)
Redis Sentinel 相关名词解释 名词 逻辑结构 物理结构 主节点 Redis 主服务 一个独立的 redis-server 进程 从节点 Redis 从服务 一个独立的 redis-server 进程 Redis 数据节点 主从节点 主节点和从节点的进程 哨兵节点 监控 Redis 数据节点的节点 一个独立的 re…...

论文阅读:H-ViT,一种用于医学图像配准的层级化ViT
来自CVPR的一篇文章,用CNNTransformer混合模型做图像配准。可变形图像配准是一种在相同视场内比较或整合单模态或多模态视觉数据的技术,它旨在找到两幅图像之间的非线性映射关系。 1,模型结构 首先,使用类似特征金字塔网络&#…...
【MySQL】(基础篇七) —— 通配符和正则表达式
通配符和正则表达式 本章介绍什么是通配符、如何使用通配符以及怎样使用LIKE操作符进行通配搜索,以便对数据进行复杂过滤;如何使用正则表达式来更好地控制数据过滤。 目录 通配符和正则表达式LIKE操作符百分号(%)通配符下划线(_)通配符 通配符使用技巧正…...

HTML静态网页成品作业(HTML+CSS)—— 名人霍金介绍网页(6个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有6个页面。 二、作品演示 三、代…...
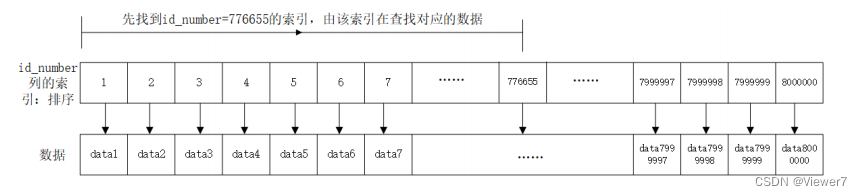
MySQL: 索引与事务
文章目录 1. 索引 (Index)1.1 概念1.2 作用1.3 使用场景1.4 索引的使用1.5 索引的使用案例 (不要轻易尝试)1.6 索引背后的数据结构1.7 重点总结 2.事务2.1 为什么要使用事务2.2 事务的概念2.3 事务的使用2.4 对事务的理解2.5 事务的基本特性 1. 索引 (Index) 1.1 概念 索引是…...

2024年最新Microsoft Edge关闭自动更新的方法分享
这里写自定义目录标题 打开【服务】 打开【服务】 windows中搜索服务,如下图: 打开服务界面,找到“Microsoft Edge Update Service (edgeupdate)” 及 “Microsoft Edge Update Service (edgeupdatem)” 两个服务,设置为禁用...

Unity3D TextMeshPro组件使用及优化详解
在Unity3D游戏开发中,文本渲染是一个不可或缺的部分。而TextMeshPro作为Unity的一个插件,提供了更高质量、更灵活的文本渲染功能,为开发者带来了极大的便利。本文将详细介绍TextMeshPro组件的使用技巧以及优化方法,并通过代码实例…...

react 0至1 【jsx】
1.函数调用 // 项目的根组件 // App -> index.js -> public/index.html(root)const count 100function getName () {return test }function App () {return (<div className"App">this is App{/* 使用引号传递字符串 */}{this is message}{/* 识别js变…...

算法训练营day58
题目1:392. 判断子序列 - 力扣(LeetCode) 暴力解法 class Solution { public:bool isSubsequence(string s, string t) {if(s.size() > t.size()) return false;if(s.size() < t.size()) {swap(s, t);}bool reslut false;int flag …...

JAVA面试中,面试官最爱问的问题。
解释Java中的抽象类和接口的区别。 在Java中,抽象类和接口都是用来定义类的抽象行为和特性的,但它们有一些关键区别: ### 抽象类 1. **定义**:抽象类是使用abstract关键字修饰的类,不能被实例化,只能被继…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
