DeepSORT(目标跟踪算法)中的状态向量与状态转移矩阵
DeepSORT(目标跟踪算法)中的状态向量与状态转移矩阵
flyfish
状态转移矩阵(State Transition Matrix)F的构造
这篇是一定要看的,拖到文章的最后部分,需要理解状态转移矩阵怎么来的,怎么是这个样子
状态向量(State Vector)
状态向量描述系统在某个时间点的完整状态。它通常包括多个变量,例如位置、速度、加速度等,具体取决于系统的动态特性。
- 记作 x k \mathbf{x}_k xk,其中 k k k 是时间步长。
状态转移矩阵(State Transition Matrix)
状态转移矩阵描述系统从一个时间点到下一个时间点的状态变化。它反映了状态向量的演化。
-
记作 A k \mathbf{A}_k Ak,用于将状态向量从 x k − 1 \mathbf{x}_{k-1} xk−1 转移到 x k \mathbf{x}_k xk:
x k = A k − 1 x k − 1 + B k − 1 u k − 1 + w k − 1 \mathbf{x}_k = \mathbf{A}_{k-1} \mathbf{x}_{k-1} + \mathbf{B}_{k-1} \mathbf{u}_{k-1} + \mathbf{w}_{k-1} xk=Ak−1xk−1+Bk−1uk−1+wk−1 -
状态向量与状态转移矩阵:状态转移矩阵 A k \mathbf{A}_k Ak 描述了状态向量 x k \mathbf{x}_k xk 如何从时间 k − 1 k-1 k−1 转移到时间 k k k。例如,对于一个简单的运动模型,状态向量可能包括位置和速度,而状态转移矩阵描述了位置和速度在每个时间步长中的变化。例如,对于一个匀速直线运动模型,状态向量和状态转移矩阵可以表示为: x k = [ x k x ˙ k ] , A k = [ 1 Δ t 0 1 ] \mathbf{x}_k = \begin{bmatrix} x_k \\ \dot{x}_k \end{bmatrix}, \quad \mathbf{A}_k = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} xk=[xkx˙k],Ak=[10Δt1]这里, Δ t \Delta t Δt 是时间步长。
假设我们要跟踪一个在平面上运动的物体,其状态包括位置和速度:
- 状态向量 x k \mathbf{x}_k xk: x k = [ x k y k x ˙ k y ˙ k ] \mathbf{x}_k = \begin{bmatrix} x_k \\ y_k \\ \dot{x}_k \\ \dot{y}_k \end{bmatrix} xk= xkykx˙ky˙k 这里 x k x_k xk 和 y k y_k yk 是位置, x ˙ k \dot{x}_k x˙k 和 y ˙ k \dot{y}_k y˙k 是速度。
- 状态转移矩阵 A k \mathbf{A}_k Ak: A k = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] \mathbf{A}_k = \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Ak= 10000100Δt0100Δt01 这表示位置随时间步长 Δ t \Delta t Δt 变化。
状态预测
给定当前时间步长 k − 1 k-1 k−1 的状态向量 x k − 1 \mathbf{x}_{k-1} xk−1 和状态转移矩阵 A k − 1 \mathbf{A}_{k-1} Ak−1,下一个时间步长 k k k 的预测状态向量 x ^ k ∣ k − 1 \hat{\mathbf{x}}_{k|k-1} x^k∣k−1 可以表示为:
x ^ k ∣ k − 1 = A k − 1 x k − 1 + B k − 1 u k − 1 \hat{\mathbf{x}}_{k|k-1} = \mathbf{A}_{k-1} \mathbf{x}_{k-1} + \mathbf{B}_{k-1} \mathbf{u}_{k-1} x^k∣k−1=Ak−1xk−1+Bk−1uk−1
- A k − 1 \mathbf{A}_{k-1} Ak−1 是状态转移矩阵,描述了系统的动态特性。
- B k − 1 \mathbf{B}_{k-1} Bk−1 是控制输入矩阵,描述了控制输入如何影响系统状态。
- u k − 1 \mathbf{u}_{k-1} uk−1 是控制输入向量,包含外部施加的控制量。
误差协方差预测
误差协方差矩阵 P k ∣ k − 1 \mathbf{P}_{k|k-1} Pk∣k−1 也需要更新,以反映预测状态的不确定性。预测步骤的误差协方差矩阵更新公式为:
P k ∣ k − 1 = A k − 1 P k − 1 ∣ k − 1 A k − 1 T + Q k − 1 \mathbf{P}_{k|k-1} = \mathbf{A}_{k-1} \mathbf{P}_{k-1|k-1} \mathbf{A}_{k-1}^T + \mathbf{Q}_{k-1} Pk∣k−1=Ak−1Pk−1∣k−1Ak−1T+Qk−1
- P k − 1 ∣ k − 1 \mathbf{P}_{k-1|k-1} Pk−1∣k−1 是当前时间步长 k − 1 k-1 k−1 的误差协方差矩阵。
- Q k − 1 \mathbf{Q}_{k-1} Qk−1 是过程噪声协方差矩阵,反映了模型中未捕捉到的不确定性。
例子
假设我们要跟踪一个在平面上运动的物体,其状态向量包括位置和速度:
x k = [ x k y k x ˙ k y ˙ k ] \mathbf{x}_k = \begin{bmatrix} x_k \\ y_k \\ \dot{x}_k \\ \dot{y}_k \end{bmatrix} xk= xkykx˙ky˙k
假设物体做匀速直线运动,状态转移矩阵可以表示为:
A = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] \mathbf{A} = \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} A= 10000100Δt0100Δt01
在没有控制输入的情况下,预测状态的计算如下:
x ^ k ∣ k − 1 = A x k − 1 \hat{\mathbf{x}}_{k|k-1} = \mathbf{A} \mathbf{x}_{k-1} x^k∣k−1=Axk−1
假设上一时间步长的状态向量为:
x k − 1 = [ 10 15 1 − 1 ] \mathbf{x}_{k-1} = \begin{bmatrix} 10 \\ 15 \\ 1 \\ -1 \end{bmatrix} xk−1= 10151−1
其中,物体在位置 ( 10 , 15 ) (10, 15) (10,15) 处,速度为 ( 1 , − 1 ) (1, -1) (1,−1) 米每秒,时间步长 Δ t = 1 \Delta t = 1 Δt=1 秒。
状态转移计算为:
x ^ k ∣ k − 1 = [ 1 0 1 0 0 1 0 1 0 0 1 0 0 0 0 1 ] [ 10 15 1 − 1 ] = [ 10 + 1 15 − 1 1 − 1 ] = [ 11 14 1 − 1 ] \hat{\mathbf{x}}_{k|k-1} = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 10 \\ 15 \\ 1 \\ -1 \end{bmatrix} = \begin{bmatrix} 10 + 1 \\ 15 - 1 \\ 1 \\ -1 \end{bmatrix} = \begin{bmatrix} 11 \\ 14 \\ 1 \\ -1 \end{bmatrix} x^k∣k−1= 1000010010100101 10151−1 = 10+115−11−1 = 11141−1
因此,通过状态转移矩阵,得到了下一个时间步长的预测状态向量 x ^ k ∣ k − 1 = [ 11 14 1 − 1 ] \hat{\mathbf{x}}_{k|k-1} = \begin{bmatrix} 11 \\ 14 \\ 1 \\ -1 \end{bmatrix} x^k∣k−1= 11141−1 。
在卡尔曼滤波中,控制输入(control input)指的是系统在每个时间步长可以施加的外部影响或干预。控制输入常用于表示可以影响系统状态的外部因素,例如驾驶员对汽车的操控、无人机的推力指令等。
控制输入的作用
控制输入用于描述外部控制如何影响系统状态的变化。它在状态转移方程中起到了修正预测状态的作用,帮助更准确地反映系统的动态。
控制输入的数学描述
状态转移方程中引入控制输入项,使状态更新更全面:
x k = A k − 1 x k − 1 + B k − 1 u k − 1 + w k − 1 \mathbf{x}_k = \mathbf{A}_{k-1} \mathbf{x}_{k-1} + \mathbf{B}_{k-1} \mathbf{u}_{k-1} + \mathbf{w}_{k-1} xk=Ak−1xk−1+Bk−1uk−1+wk−1
其中:
- A k − 1 \mathbf{A}_{k-1} Ak−1:状态转移矩阵,描述系统的内在动力学。
- B k − 1 \mathbf{B}_{k-1} Bk−1:控制输入矩阵,描述控制输入对系统状态的影响。
- u k − 1 \mathbf{u}_{k-1} uk−1:控制输入向量,表示外部施加的控制。
- w k − 1 \mathbf{w}_{k-1} wk−1:过程噪声,表示模型中未捕捉到的随机扰动。
示例
假设我们在跟踪一辆汽车,状态向量包括位置和速度:
x k = [ x k x ˙ k ] \mathbf{x}_k = \begin{bmatrix} x_k \\ \dot{x}_k \end{bmatrix} xk=[xkx˙k]
无控制输入的情况
状态转移矩阵假设汽车做匀速运动:
A = [ 1 Δ t 0 1 ] \mathbf{A} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} A=[10Δt1]
预测下一时间步的状态为:
x ^ k ∣ k − 1 = A x k − 1 \hat{\mathbf{x}}_{k|k-1} = \mathbf{A} \mathbf{x}_{k-1} x^k∣k−1=Axk−1
有控制输入的情况
假设汽车可以通过加速或减速改变速度,控制输入向量表示加速度:
u k = a k \mathbf{u}_k = a_k uk=ak
控制输入矩阵描述加速度对速度和位置的影响:
B = [ 0.5 Δ t 2 Δ t ] \mathbf{B} = \begin{bmatrix} 0.5 \Delta t^2 \\ \Delta t \end{bmatrix} B=[0.5Δt2Δt]
状态转移方程引入控制输入后变为:
x ^ k ∣ k − 1 = A x k − 1 + B u k − 1 \hat{\mathbf{x}}_{k|k-1} = \mathbf{A} \mathbf{x}_{k-1} + \mathbf{B} \mathbf{u}_{k-1} x^k∣k−1=Axk−1+Buk−1
具体计算
假设上一时间步的状态向量为:
x k − 1 = [ 10 5 ] \mathbf{x}_{k-1} = \begin{bmatrix} 10 \\ 5 \end{bmatrix} xk−1=[105]
其中,位置为10米,速度为5米每秒。时间步长 Δ t = 1 \Delta t = 1 Δt=1 秒。
如果加速度为2米每秒平方( a k = 2 a_k = 2 ak=2),则控制输入向量为:
u k − 1 = 2 \mathbf{u}_{k-1} = 2 uk−1=2
状态转移矩阵和控制输入矩阵为:
A = [ 1 1 0 1 ] , B = [ 0.5 1 ] \mathbf{A} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 0.5 \\ 1 \end{bmatrix} A=[1011],B=[0.51]
预测下一时间步的状态为:
x ^ k ∣ k − 1 = A x k − 1 + B u k − 1 = [ 1 1 0 1 ] [ 10 5 ] + [ 0.5 1 ] ⋅ 2 = [ 15 5 ] + [ 1 2 ] = [ 16 7 ] \hat{\mathbf{x}}_{k|k-1} = \mathbf{A} \mathbf{x}_{k-1} + \mathbf{B} \mathbf{u}_{k-1} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 10 \\ 5 \end{bmatrix} + \begin{bmatrix} 0.5 \\ 1 \end{bmatrix} \cdot 2 = \begin{bmatrix} 15 \\ 5 \end{bmatrix} + \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} 16 \\ 7 \end{bmatrix} x^k∣k−1=Axk−1+Buk−1=[1011][105]+[0.51]⋅2=[155]+[12]=[167]
因此,通过引入控制输入,预测得到下一时间步的位置为16米,速度为7米每秒。
在卡尔曼滤波中,测量向量通过观测矩阵可以得到与实际测量值进行比较的预测测量值。这是滤波器更新步骤中的一个关键部分,用于校正预测的状态。
相关文章:
中的状态向量与状态转移矩阵)
DeepSORT(目标跟踪算法)中的状态向量与状态转移矩阵
DeepSORT(目标跟踪算法)中的状态向量与状态转移矩阵 flyfish 状态转移矩阵(State Transition Matrix)F的构造 这篇是一定要看的,拖到文章的最后部分,需要理解状态转移矩阵怎么来的,怎么是这个…...
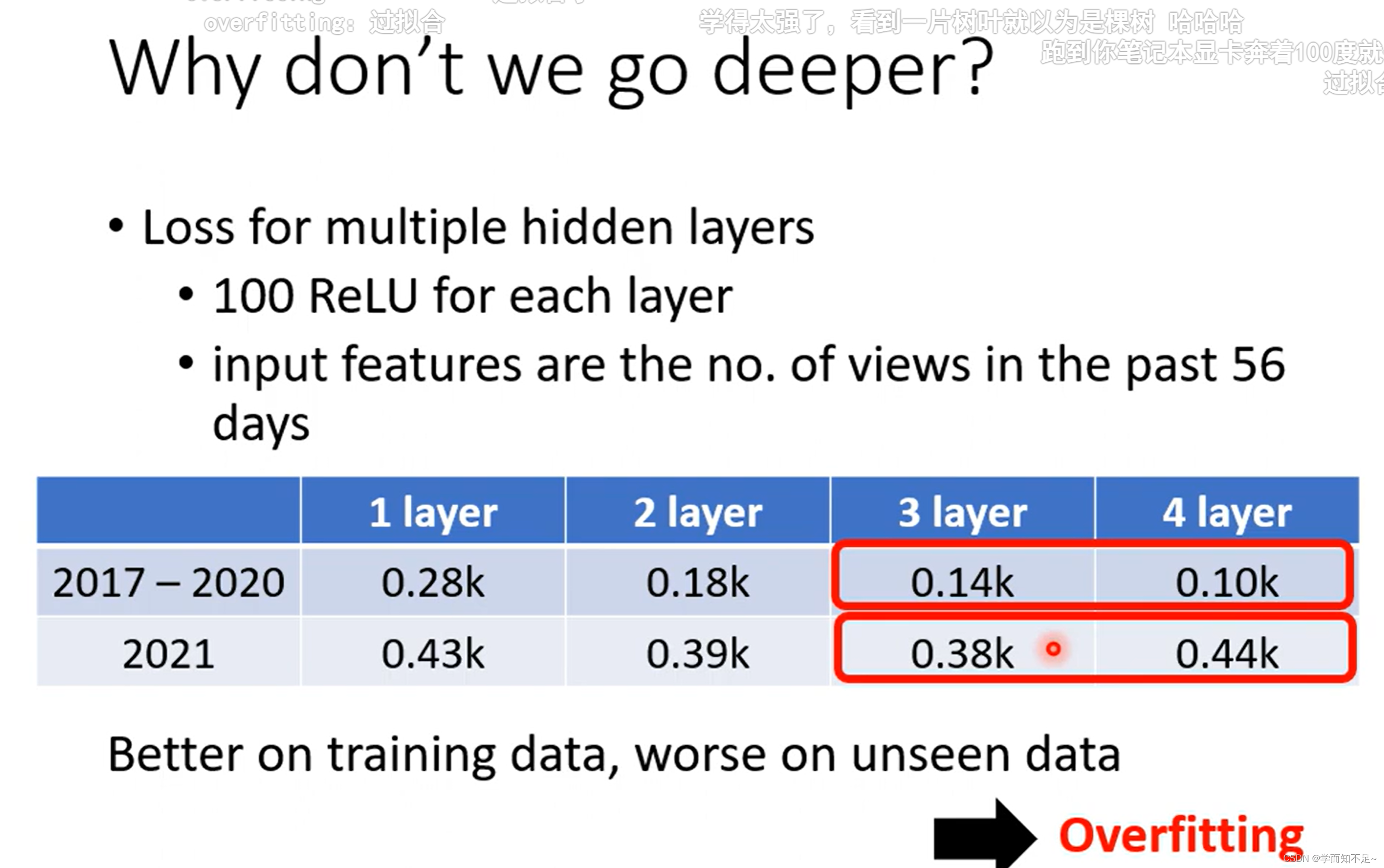
李宏毅深度学习01——基本概念简介
视频链接 基本概念 Regression(回归): 类似于填空 Classification(分类): 类似于选择 Structure Learning(机器学习): ?? 机器学习找对应函数…...
TcpClient 服务器、客户端连接
TcpClient 服务器 TcpListener 搭建tcp服务器的类,基于socket套接字通信的 1 创建服务器对象 TcpListener server new TcpListener(IPAddress.Parse("127.0.0.1"), 3000); 2 开启服务器 设置最大连接数 server.Start(1000); 3 接收客户端的链接,只能…...
13大最佳工程项目管理系统软件盘点
国内外主流的13款工程项目管理系统软件:Worktile、中建软件、泛微建筑项目管理软件、LiquidPlanner、Wrike、建文软件、广联达、Microsoft Project、泛普软件、Procore、Buildertrend、Fieldwire、Autodesk Construction Cloud。 在快速变化的工程领域,有…...
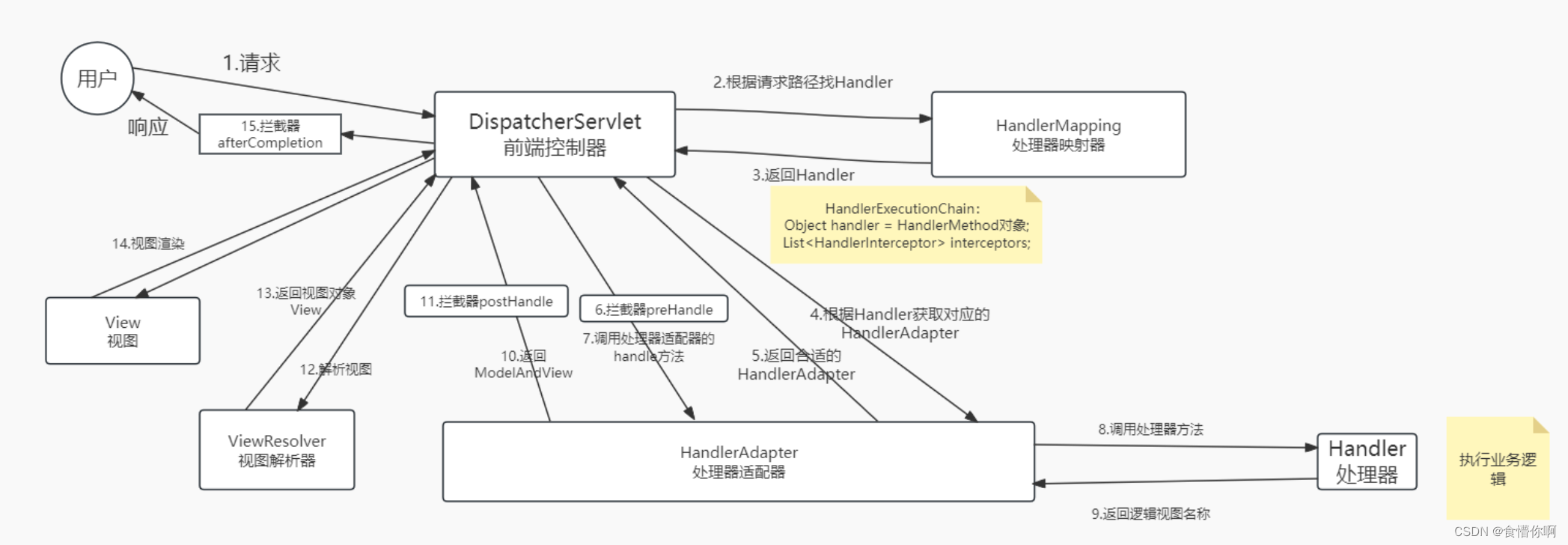
SpringMVC:拦截器(Interceptor)
1. 简介 拦截器(Interceptor)类似于过滤器(Filter) Spring MVC的拦截器作用是在请求到达控制器之前或之后进行拦截,可以对请求和响应进行一些特定的处理。拦截器可以用于很多场景下: 1. 登录验证…...

【Python】selenium使用find_element时解决【NoSuchWindowException】问题的方法
NoSuchWindowException 是 Selenium WebDriver 中的一种异常,当尝试切换到一个不存在的窗口时,或者在尝试获取窗口句柄时窗口已经关闭或不存在,就会抛出这个异常。 以下是一些解决 NoSuchWindowException 的常见方法: 检查窗口是…...

PTA:7-188 水仙花数
作者 王秀秀 单位 山东交通学院 任务描述 本关任务:输出100到999之间的所有的“水仙花数”。所谓的“水仙花数”是指一个3位数,其各位数字立方和等于该数本身。 例如,153是一个水仙花数,因为 15313 53 33 提示 关键在于对一…...

HTML静态网页成品作业(HTML+CSS+JS)—— 美食企业曹氏鸭脖介绍网页(4个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,使用Javacsript代码实现 图片轮播切换,共有4个页面。 二、…...
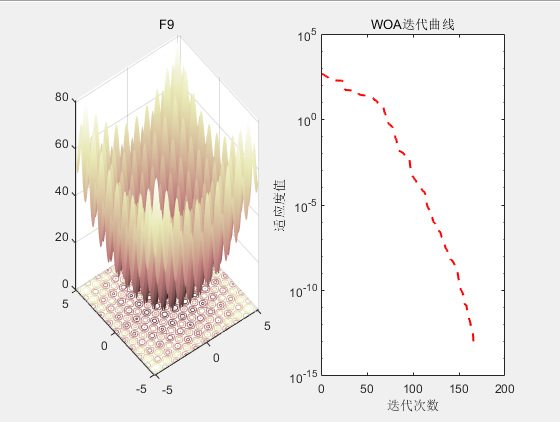
SCI二区|鲸鱼优化算法(WOA)原理及实现【附完整Matlab代码】
目录 1.背景2.算法原理2.1算法思想 3.结果展示4.参考文献5.代码获取 1.背景 2016年,S Mirjalili受到自然界座头鲸社会行为启发,提出了鲸鱼优化算法(Whale Optimization Algorithm, WOA)。 2.算法原理 WOA模拟了座头鲸的社会行为…...
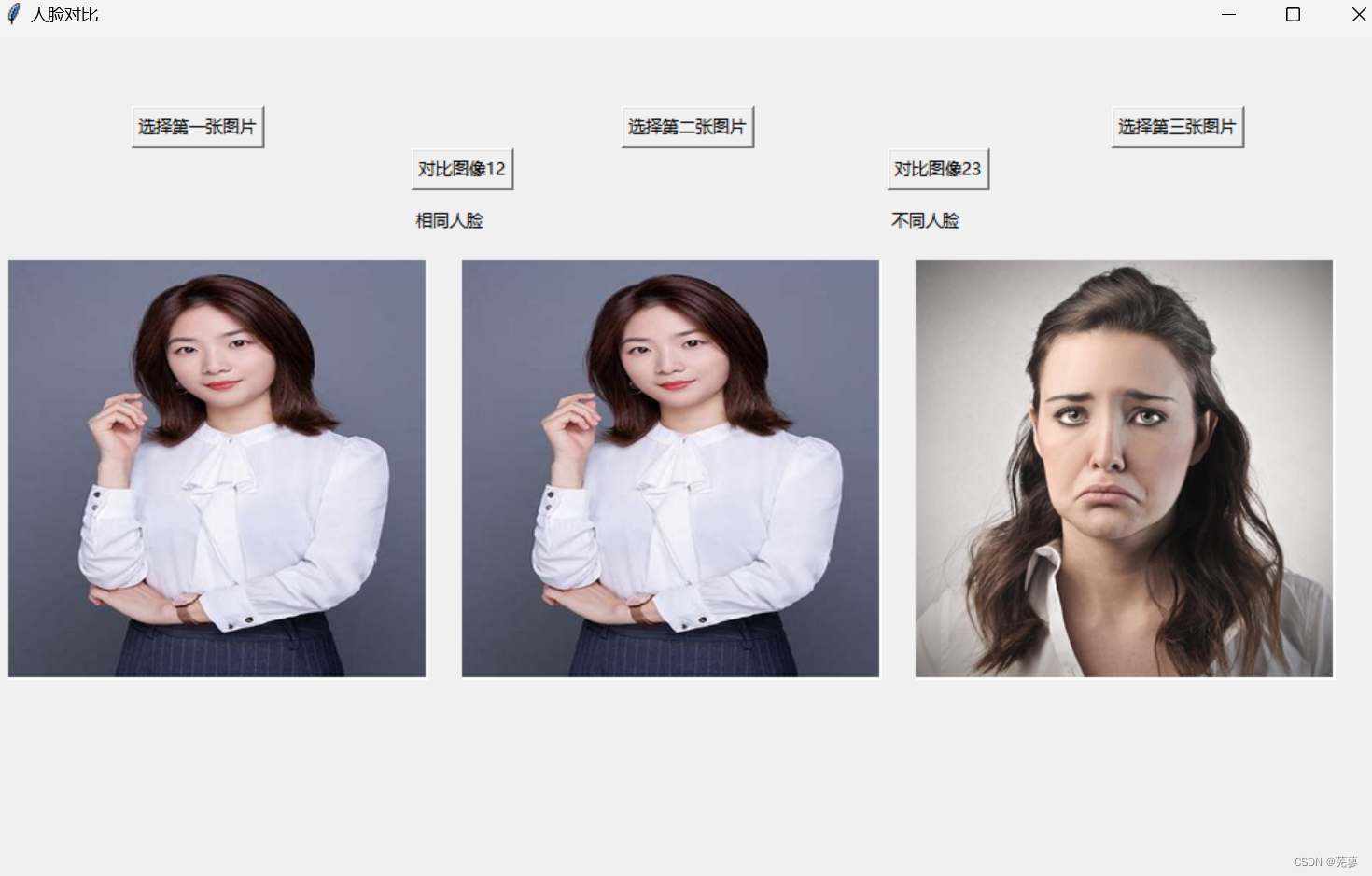
人脸匹配——OpenCV
人脸匹配 导入所需的库加载dlib的人脸识别模型和面部检测器读取图片并转换为灰度图比较两张人脸选择图片并显示结果比较图片创建GUI界面运行GUI主循环运行显示全部代码 导入所需的库 cv2:OpenCV库,用于图像处理。 dlib:一个机器学习库&#x…...
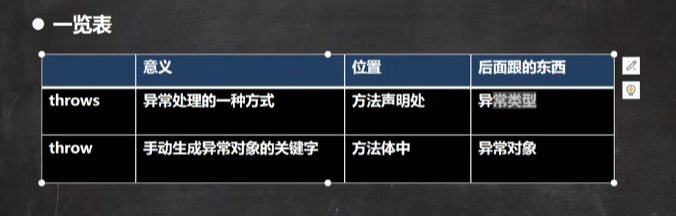
韩顺平0基础学java——第22天
p441-459 异常exception 选中代码块,快捷键ctraltt6,即trt-catch 如果进行了异常处理,那么即使出现了异常,但是会继续执行 程序过程中发生的异常事件分为两大类: 异常体系图※ 常见的运行异常:类型转换…...

神经网络介绍及教程案例
神经网络介绍及教程&案例 神经网络(Neural Networks)是机器学习和人工智能中的一种关键技术,模仿了人类大脑的工作方式,能够处理复杂的数据和任务。以下是神经网络的一些基础介绍: 基本概念 神经元(N…...
16个不为人知的资源网站,强烈建议收藏!
整理了16个不为人知的资源网站,涵盖了课程学习、办公技能、娱乐休闲、小说音乐等多种资源,强烈建议收藏! #学习网站 1、中国大学MOOC icourse163.org/ 这是一个汇集了国内顶尖大学免费课程资源的平台,众多985工程院校如北京大…...

pandas获取某列最大值的所有数据
第一种方法: 按照某列进行由大到小的排序,然后再进去去重,保留第一个值,最终保留的结果就是最大值的数据 # 由大到小排序 data_frame data_frame.sort_values(bycolumn_a, ascendingFalse)# 按照column_b列去重保留第一条&#…...
App UI 风格展现非凡创意
App UI 风格展现非凡创意...
rocketmq-5.1.2的dleger高可用集群部署
1、背景 原先为5.0.0版本,因检查出有漏洞,升级到5.1.2版本。 【Rocketmq是阿里巴巴在2012年开发的分布式消息中间件,专为万亿级超大规模的消息处理而设计,具有高吞吐量、低延迟、海量堆积、顺序收发等特点。在一定条件下…...

无线网络与物联网技术[1]之近距离无线通信技术
无线网络与物联网技术 近距离无线通信技术WIFIWi-Fi的协议标准Wi-Fi的信道Wi-Fi技术的术语Wi-Fi的组网技术Ad-hoc模式无线接入点-APAP:FAT AP vs FIT AP Wi-Fi的特点与应用Wi-Fi的安全技术 Bluetooth蓝牙技术概论蓝牙的技术协议蓝牙的组网技术微微网piconet(了解)散…...
)
Codeforces Round 952 (Div. 4)
题解写到博客园了,懒得复制过来了了,放个链接 https://www.cnblogs.com/yxcblogs/p/18243276 推广一下自己记录的算法编程竞赛模板仓库 GitHub - yxc-s/programming-template: This repository contains C programming templates optimized for competi…...
 中的聚类算法Bisecting K-Means、K-Means、Gaussian Mixture)
spark MLlib (DataFrame-based) 中的聚类算法Bisecting K-Means、K-Means、Gaussian Mixture
Bisecting K-Means 核心原理: Bisecting K-Means 是一种层次 K-Means 聚类算法,基于 Steinbach、Karypis 和 Kumar 的论文《A comparison of document clustering techniques》,并对 Spark 环境进行了修改和适应。 该算法通过递归地将数据集…...

天降流量于雀巢?元老品牌如何创新营销策略焕新生
大家最近有看到“南京阿姨手冲咖啡”的视频吗?三条雀巢速溶咖啡入杯,当面加水手冲,十元一份售出,如此朴实的售卖方式迅速在网络上走红。而面对这一波天降的热度,雀巢咖啡迅速做出了回应,品牌组特地去到了阿…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
