多源最短路径算法 -- 弗洛伊德(Floyd)算法
1. 简介
Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德的名字命名。
2. 核心思想
通过考虑图中所有可能的中转点,逐步更新两点间的最短路径长度和路径信息,直至找到最终的最短路径。有的人也称之为插点法。
3. 图解
3.1 初始化
初始化:设置图的邻接矩阵dict,其中dict[i][j]表示顶点i到顶点j的直接路径权重;如果两顶点不直接相连,则设为无穷大INF。
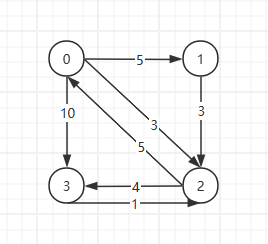
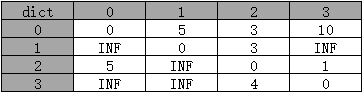
3.2 更新最短路径
更新最短路径:把每个节点当作是中转节点,更新矩阵中的距离。
通过中间顶点 k 从顶点 i 到顶点 j 的距离 小于 直接从顶点 i 到顶点 j 的距离,更新 dist[i][j] = dist[i][k] + dist[k][j]。
把0作为中转节点,此时表中黄色部分是不需要改的(都是从0出发或是直接到0的距离),
当更新 dict[1][2]也就是1 -> 2 时,需判断 1 -> 0 和 0 -> 2 的和是否比直达的1 -> 2更小。
若路径中有INF就无需更新,比如此时1 -> 0 就是INF,表示1 -> 2 以 0 作为中转点时不可能比 1 -> 2 直达的更小,所以此时不需要更新。
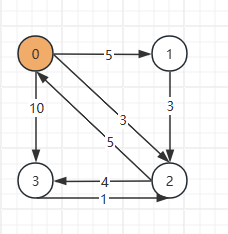
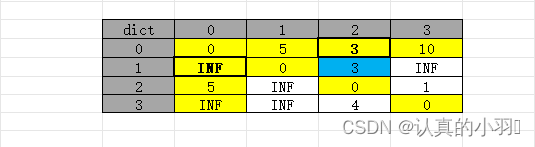
更新完 0作为中转节点时 数组为:

更新完 1作为中转节点时 数组为:
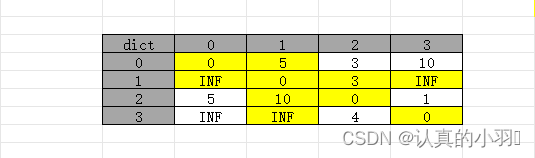
更新完 2作为中转节点时 数组为:

更新完 3作为中转节点时 数组为:

3.3 结果
最终结果的数组中就是点到点的最短路径。
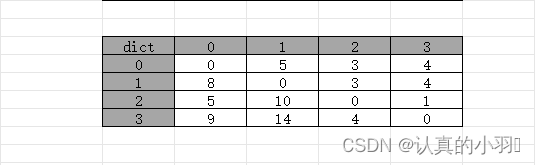
4. 代码实现
定义了一个4x4的图,其中INF表示两个顶点之间没有直接相连的边。然后调用floyd方法计算所有顶点对之间的最短路径,并输出结果。
public class Floyd {private static final int INF = Integer.MAX_VALUE; public static void floyd(int[][] graph) {int n = graph.length; // 获取图的顶点数int[][] dist = new int[n][n]; // 初始化矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dist[i][j] = graph[i][j]; }}// 使用Floyd算法计算所有顶点之间的最短路径for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][k] != INF && dist[k][j] != INF&& dist[i][k] + dist[k][j] < dist[i][j]) { // 更新i到j的最短路径dist[i][j] = dist[i][k] + dist[k][j];}}}}// 输出所有顶点之间的最短路径for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.print(dist[i][j] + " ");}System.out.println();}}public static void main(String[] args) {int[][] graph = {{0, 5 , 3 , 10 },{INF, 0 , 3 , INF},{5 , INF, 0 , 1 },{INF, INF, 4 , 0 }};floyd(graph); }
}
5. floyd算法和Dijkstra算法的区别
Floyd算法和Dijkstra算法都是计算图中顶点之间最短路径的著名算法,但它们的应用场景、原理和性能存在显著差异。具体分析如下:
应用场景
- Dijkstra算法:适用于单源最短路径问题,即从单个源点到其他所有点的最短路径。它不能处理具有负权边的图。
- Floyd算法:用于求解任意顶点对(多源最短路径问题)的最短路径,可以处理负权边,但不能处理包含负权回路的图。
算法原理
- Dijkstra算法:基于贪心策略,每次从未确定的顶点中选择一个距离源点最近的顶点,然后更新其邻接顶点的距离。该算法需要使用优先队列来选择下一个顶点,并且初始时除源点外的所有顶点的距离都设置为无穷大。
- Floyd算法:通过动态规划的方式,利用三层嵌套循环来计算所有顶点对之间的最短路径。算法的基本操作是比较(u,k) + (k,v)与(u,v)的长度,并据此更新(u,v)的长度。
时间复杂度
- Dijkstra算法:使用优先队列优化后的时间复杂度是O((V+E) log V),其中V是顶点数,E是边数。如果使用邻接矩阵实现且没有优化,复杂度会是O(V^2)。
- Floyd算法:时间复杂度为O(V^3),因为算法需要三层循环遍历所有顶点对和可能的中间顶点。
额外功能
- Dijkstra算法:可以输出从源点到各顶点的最短路径。
- Floyd算法:可以输出任意两个顶点间的最短路径及其长度。
总之,Dijkstra算法适合解决单源最短路径问题,尤其是在没有负权边的情况下,而Floyd算法适合解决所有顶点对之间的最短路径问题,尽管它可以处理负权边的情况,却不能容忍负权回路的存在。
6. 总结
总的来说,Floyd算法是一种计算图中所有顶点对之间最短路径的动态规划算法,它能够处理包含负权边的图,但不允许存在负权回路。适用于小型到中等规模稠密图的算法,尤其是在需要全局最短路径信息时。对于大型稀疏图或者单源最短路径问题,其他算法如Dijkstra算法可能更加合适。
相关文章:

多源最短路径算法 -- 弗洛伊德(Floyd)算法
1. 简介 Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特弗洛伊德的名字命名。 2. 核心思…...

同三维T80005EH4 H.265 4路高清HDMI编码器
同三维T80005EH4 H.265 4路高清HDMI编码器 4路HDMI输入2路3.5音频输入,第1路和第2路HDMI可支持4K30,其它支持高清1080P60 产品简介: 同三维T80005EH4 4路HDMI高清H.265编码器采用最新高效H.265高清数字视频压缩技术,具备稳定…...

焦化行业排放平台简介
在当今社会,环保事业日益受到人们的关注。焦化行业作为重要的工业领域之一,其排放问题一直是环保工作的重点。为了有效控制焦化行业的排放,实施焦化行业排放平台成为了必不可少的措施。朗观视觉小编将详细探讨焦化行业排放平台的实施范围&…...
『原型资源』Axure自带图标库不够用,第三方经典图标库来袭
今天小编为大家带来第三方经典图标库,己确认内容可用现推荐给大家。直接上手就可不用自己画哈~ 获取原型文档请与班主任联系! 先睹为快,合适再拿走不谢: 图标太多,截取部分给大家参考o(* ̄︶ ̄*…...

修改版的VectorDBBench更好用
原版本VectorDBBench的几个问题 在这里就不介绍VectorDBBench是干什么的了,上官网即可。 1.并发数设置的太少 2.测试时长30秒太长 3.连接milvus无用户和密码框,这个是最大的问题 4.修改了一下其它参数 由于很多网友发私信问一些milvus的相关技术问…...

六西格玛培训都培训哪些内容 ?
天行健六西格玛培训的内容通常涵盖多个方面,旨在帮助学员全面理解和应用六西格玛管理方法。以下是详细的培训内容概述: 一、六西格玛基础知识 引入六西格玛的概念、原理和历史,包括DMAIC(定义、测量、分析、改进、控制࿰…...

K8S环境部署Prometheus
K8S环境部署Prometheus 记录在K8S 1.18版本环境下部署Prometheus 0.5版本。 1. 下载kube-prometheus仓库 git clone https://github.com/coreos/kube-prometheus.git cd kube-prometheus笔者安装的K8S版本是1.18 ,prometheus选择配套的分支release-0.5࿱…...

在linux系统上挂载新硬盘
服务器的硬盘空间不够了,自己重新安装了一个硬盘,需要挂载,因为只是用来存放数据,所以不需要分区,直接挂载就可以 #查看当前所有硬盘 sudo fdisk -l #用于显示文件系统的磁盘空间使用情况 df -h发现一个/dev/nvme0n1 …...

1004.最大连续1的个数
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 示例 1: 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字…...

【机器学习300问】116、什么是序列模型?序列模型能干什么?
一、序列模型是什么? 序列模型是机器学习领域中专门设计来处理具有时间顺序或序列结构数据的模型。这类模型能够理解和学习数据中的顺序依赖关系,因此非常适合诸如自然语言处理、语音识别、音乐生成、时间序列预测等任务。 看了上面的定义,似…...

kafka 快速上手
下载 Apache Kafka 演示window 安装 编写启动脚本,脚本的路径根据自己实际的来 启动说明 先启动zookeeper后启动kafka,关闭是先关kafka,然后关闭zookeeper 巧记: 铲屎官(zookeeper)总是第一个到,最后一个走 启动zookeeper call bi…...

Python记忆组合透明度语言模型
🎯要点 🎯浏览器语言推理识别神经网络 | 🎯不同语言秽语训练识别数据集 | 🎯交互式语言处理解释 Transformer 语言模型 | 🎯可视化Transformer 语言模型 | 🎯语言模型生成优质歌词 | 🎯模型不确…...
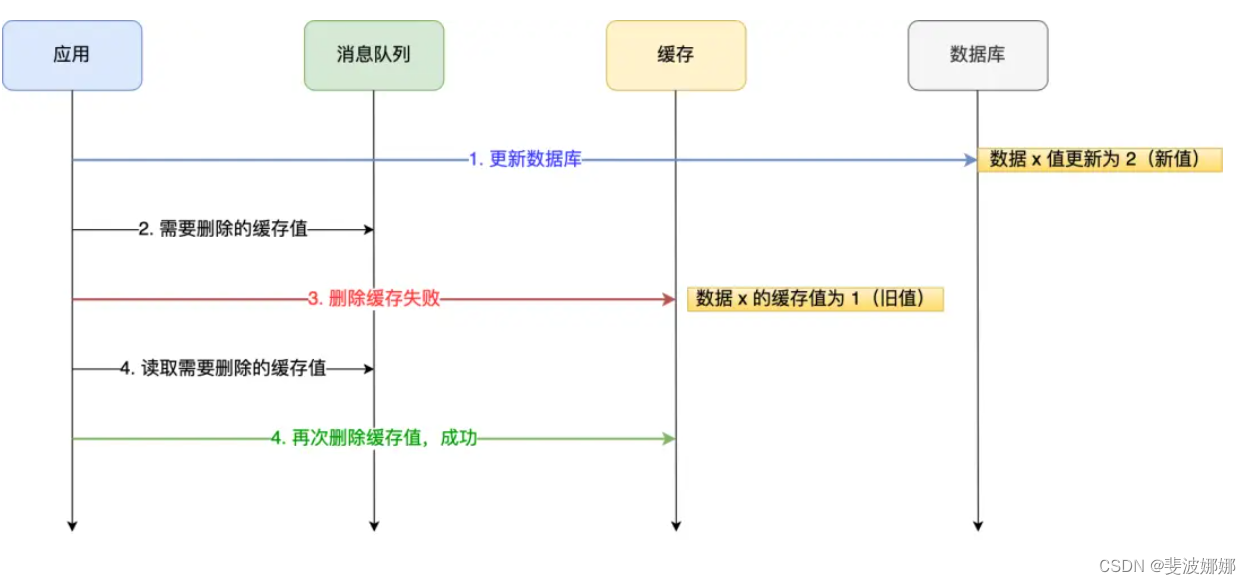
如何保证数据库和缓存的一致性
背景:为了提高查询效率,一般会用redis作为缓存。客户端查询数据时,如果能直接命中缓存,就不用再去查数据库,从而减轻数据库的压力,而且redis是基于内存的数据库,读取速度比数据库要快很多。 更新…...

Java基础 - 多线程
多线程 创建新线程 实例化一个Thread实例,然后调用它的start()方法 Thread t new Thread(); t.start(); // 启动新线程从Thread派生一个自定义类,然后覆写run()方法: public class Main {public static void main(String[] args) {Threa…...

云顶之弈-测试报告
一. 项目背景 个人博客系统采用前后端分离的方法来实现,同时使用了数据库来存储相关的数据,同时将其部署到云服务器上。前端主要有四个页面构成:登录页、列表页、详情页以及编辑页,以上模拟实现了最简单的个人博客系统。其结合后…...
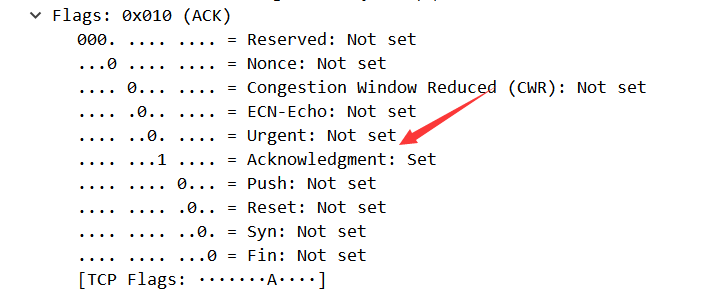
TCP/IP协议分析实验:通过一次下载任务抓包分析
TCP/IP协议分析 一、实验简介 本实验主要讲解TCP/IP协议的应用,通过一次下载任务,抓取TCP/IP数据报文,对TCP连接和断开的过程进行分析,查看TCP“三次握手”和“四次挥手”的数据报文,并对其进行简单的分析。 二、实…...
)
Python项目开发实战:企业QQ小程序(案例教程)
一、引言 在当今数字化快速发展的时代,企业对于线上服务的需求日益增长。企业QQ小程序作为一种轻量级的应用形态,因其无需下载安装、即开即用、占用内存少等优势,受到了越来越多企业的青睐。本文将以Python语言为基础,探讨如何开发一款企业QQ小程序,以满足企业的实际需求。…...

list模拟与实现(附源码)
文章目录 声明list的简单介绍list的简单使用list中sort效率测试list的简单模拟封装迭代器insert模拟erase模拟头插、尾插、头删、尾删模拟自定义类型迭代器遍历const迭代器clear和析构函数拷贝构造(传统写法)拷贝构造(现代写法) 源…...

Java应用中文件上传安全性分析与安全实践
✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心哦!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 一. 文件上传的风险 二. 使用合适的框架和库 1. Spr…...
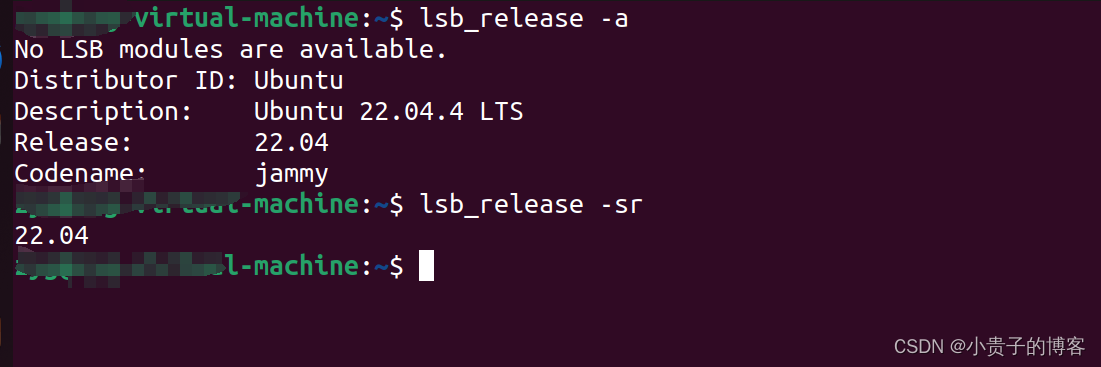
noVNC 小记
1. 怎么查看Ubuntu版本...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
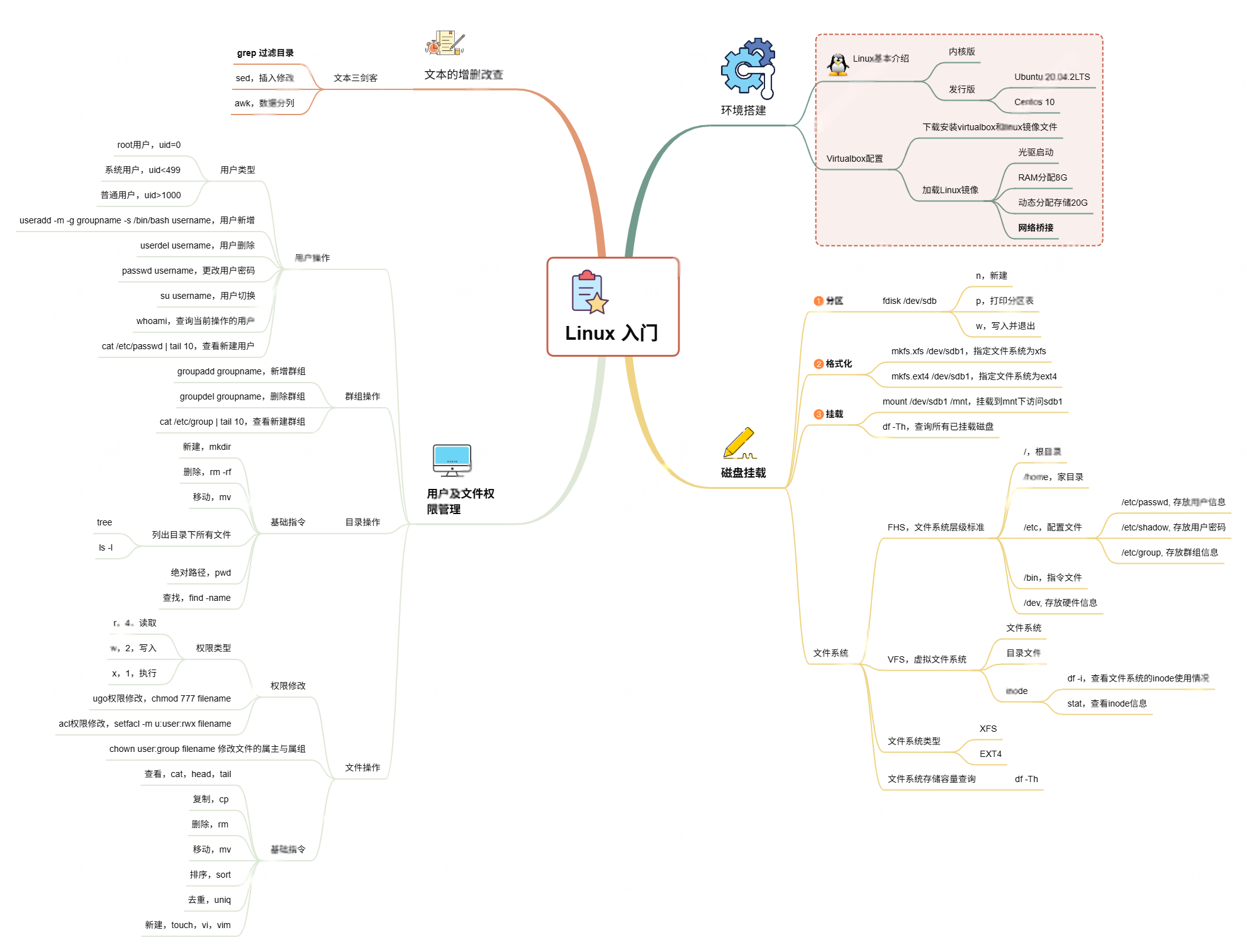
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
