C++算法-青蛙跳台阶【面试】
"青蛙跳台阶"问题是一个经典的递归问题,也与斐波那契数列有关。问题是这样的:一只青蛙站在一个n阶台阶上,它每次可以跳1阶或2阶,问青蛙跳到顶端总共有多少种跳法。
这个问题可以用递归或动态规划来解决。以下是使用C++实现的动态规划解法:
#include <iostream>
#include <vector>// 动态规划解法
int climbStairs(int n) {if (n <= 2) {return n;}// 创建一个数组来存储子问题的解std::vector<int> dp(n + 1, 0);// 初始化前两个台阶的跳法dp[1] = 1;dp[2] = 2;// 计算从3阶到n阶的跳法for (int i = 3; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}// 返回n阶台阶的跳法总数return dp[n];
}int main() {int n = 5;std::cout << "Number of ways to climb " << n << " steps is: " << climbStairs(n) << std::endl;return 0;
}
这段代码中,climbStairs函数使用了一个std::vector<int>来存储子问题的解,避免了重复计算。数组dp[i]表示到达第i阶台阶的跳法数。根据题目条件,到达第i阶台阶的跳法数等于到达(i-1)阶和(i-2)阶台阶的跳法数之和。
面试回答示例:
"青蛙跳台阶问题可以通过动态规划来解决。我们首先定义一个数组dp,其中dp[i]表示到达第i阶台阶的跳法数。我们知道到达第一阶和第二阶都只有一种方法。对于更高的台阶,到达那里的方法数是到达前一阶和前两阶台阶的方法数之和,因为青蛙可以选择从这两个位置跳过来。我们从第三阶台阶开始,逐步计算直到第n阶,最终返回dp[n]作为答案。这种方法避免了递归方法中的重复计算,时间复杂度是O(n),空间复杂度也是O(n)。"
相关文章:

C++算法-青蛙跳台阶【面试】
"青蛙跳台阶"问题是一个经典的递归问题,也与斐波那契数列有关。问题是这样的:一只青蛙站在一个n阶台阶上,它每次可以跳1阶或2阶,问青蛙跳到顶端总共有多少种跳法。 这个问题可以用递归或动态规划来解决。以下是使用C实…...
)
px转rem插件postcss-plugin-px2rem使用方法(浏览器缩放页面自适应)
px转rem插件postcss-plugin-px2rem使用方法(浏览器缩放页面自适应) 1. 常见屏幕自适应的布局 百分比布局rem布局css媒体查询在前端框架设计初期,应优先选择好页面布局方式 2. postcss-plugin-px2rem插件的使用 官网地址:https…...
批量文件重命名技巧:轻松替换删除文件夹名中的字母,实现高效文件管理新境界
在数字化时代,我们每天都会面对大量的文件和文件夹。无论是工作文档、学习资料还是个人收藏,文件命名的规范性都显得尤为重要。然而,手动一个一个去修改文件名,不仅耗时耗力,还容易出错。那么,有没有一种方…...

windows设备/路由设备上ip地址如何查看、使用
在Windows设备上查看本地IP地址(IPv4和IPv6): 使用命令提示符: 打开命令提示符(在Windows中按Win R,然后输入"cmd"并按Enter)。在命令提示符窗口中,输入以下命令以查看…...

服务端⾼并发分布式结构演进之路
在进行技术学习过程中,由于大部分读者没有经历过一些中大型系统的实际经验,导致无法从全局理解一些概念,所以本文以一个"电子商务"应用为例,介绍从一百个到千万级并发情况下服务端的架构的演进过程,同时列举…...

Stable Diffusion ProtoVisionXL大模型之艺术盛宴!
今天基于ProtoVisionXL这款大模型为大家呈现一些视觉上的艺术盛宴,视觉冲击宣传海报信手拈来,再配上你的宣传语,妥妥地让人眼前一亮。 实测参数: 分辨率:768*1024 采样方法 (Sampler):DPM 2M Karras 迭代步数 (Ste…...
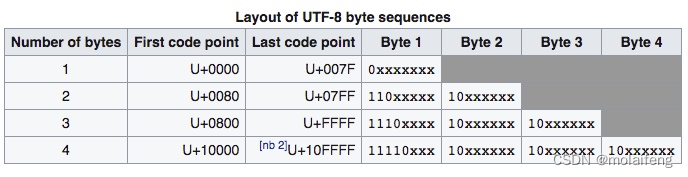
浅谈golang字符编码
1、 Golang 字符编码 Golang 的代码是由 Unicode 字符组成的,并由 Unicode 编码规范中的 UTF-8 编码格式进行编码并存储。 Unicode 是编码字符集,囊括了当今世界使用的全部语言和符号的字符。有三种编码形式:UTF-8,UTF-16&#…...

Vite和Webpack的区别是什么,你站队谁?
Vite和Webpack有很多相同之处,也有区别,很多老铁分不清,贝格前端工场借助此文为大家详细介绍一下。 一、关于Vite和Webpack Vite和Webpack都是前端开发中常用的构建工具,用于将源代码转换为可在浏览器中运行的静态资源。它们在一…...
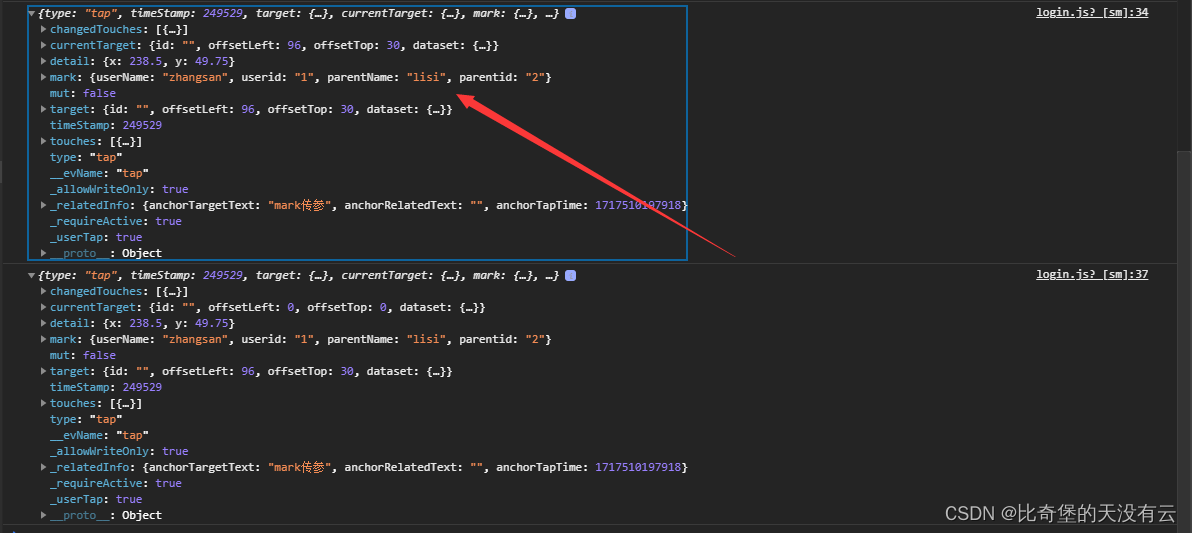
【微信小程序】事件传参的两种方式
文章目录 1.什么是事件传参2.data-*方式传参3.mark自定义数据 1.什么是事件传参 事件传参:在触发事件时,将一些数据作为参数传递给事件处理函数的过程,就是事件传参 在微信小程序中,我们经常会在组件上添加一些自定义数据,然后在…...

前端针对需要递增的固定数据
这里递增的是1到12 data(){return{cycleOptions:Array.from({ length: 12 }, (v, k) > ({value: k 1,label: String(k 1)})),} }<el-select v-model"ruleForm.monthLength" placeholder"请选择周期数量"><el-optionv-for"item in cycle…...

红酒保存中的氧气管理:适度接触与避免过度氧化
在保存云仓酒庄雷盛红酒的过程中,我们不得不面对一个微妙的问题:氧气管理。氧气,这个我们生活中无处不在的气体,对于红酒的保存却有着至关重要的影响。适度接触氧气对红酒的陈年过程和品质维护具有积极作用,然而过度氧…...

从零开始搭建开源智慧城市项目(三)上升线效果
前言 上一节实现了添加建筑物线框,模型外墙和道路地面材质添加。这一节准备通过简单的shader实现上升线效果。 思路 简单的说一下思路,通过获取模型顶点坐标所在的高度Z来进行筛选,高度再某一区间内设置成上升线的颜色,其余高度…...
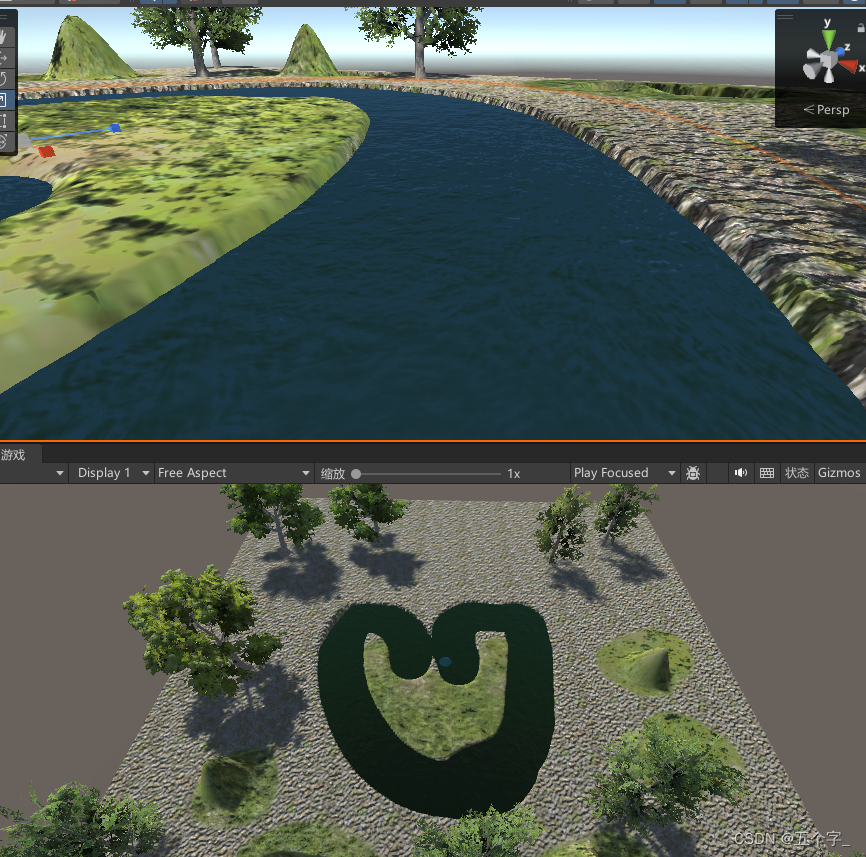
unity基础(五)地形详解
目录 一 创建地形 二 调整地形大小 三 创建相邻地形 四 创建山峰 五 创建树木 七 添加风 八 添加水 简介: Unity 中的基础地形是构建虚拟场景的重要元素之一。 它提供了一种直观且灵活的方式来创建各种地形地貌,如山脉、平原、山谷等。 通过 Unity 的地形…...

postman接口测试工具详解
Postman 是一个功能强大的 API 开发和测试工具,广泛应用于开发人员和测试人员进行 API 的调试、测试、文档生成等工作。以下是对 Postman 的详细介绍。 1. 功能概览 1.1 请求构建 请求类型: 支持 GET、POST、PUT、DELETE、PATCH、OPTIONS 等多种 HTTP 方法。URL …...
作者:————LJS)
2024年护网行动全国各地面试题汇总(3)作者:————LJS
应急响应基本思路和流程 收集信息:收集客户信息和中毒主机信息,包括样本判断类型:判断是否是安全事件,何种安全事件,勒索、挖矿、断网、DoS 等等抑制范围:隔离使受害⾯不继续扩⼤深入分析:日志分…...

计算机专业的学生要达到什么水平才能进入大厂工作?越早知道越好
计算机专业的学生要达到什么水平才能进入BAT等大厂工作?越早知道越好. 一、算法题 各大公司笔试、面试基本都考这个,别的不说,《剑指Offer》所有题目背下来,Leetcode高频题目刷个一两百遍,搞过ACM也可以,…...

巡检费时费力?试试AI自动巡检
随着企业IT规模不断增长,设备、系统越来越多,运维工作压力也与日俱增。保障设备、系统健康稳定地运行,日常巡检是运维工作不可或缺的部分。通过巡检可以及时发现设备、系统的异常问题,提前预防及时处理,避免问题扩大产…...

46-4 等级保护 - 网络安全等级保护概述
一、网络安全等级保护概述 原文:没有网络安全就没有国家安全 二、网络安全法 - 安全立法 中华人民共和国主席令 第五十三号 《中华人民共和国网络安全法》已于2016年11月7日由中华人民共和国第十二届全国人民代表大会常务委员会第二十四次会议通过,并自2017年6月1日起正式…...

css引入方式有几种?link和@import有什么区别?
在CSS中,引入外部样式表的方式主要有两种:<link>标签和import规则。 使用<link>标签引入外部样式表: <link rel"stylesheet" href"path/to/style.css">这种方式是在HTML文档的<head>部分或者…...

使用‘消除’技术绕过LLM的安全机制,不用训练就可以创建自己的nsfw模型
开源的大模型在理解和遵循指令方面都表现十分出色。但是这些模型都有审查的机制,在获得被认为是有害的输入的时候会拒绝执行指令,例如会返回“As an AI assistant, I cannot help you.”。这个安全功能对于防止误用至关重要,但它限制了模型的…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
