C语言|十进制数转换任意进制数
将十进制数转换成任意进制数。
思路分析:
先举一个具体的例子:十进制转换为二进制数
1 定义一个数组a[100],先归0,再存放运算过程中的余数
2 定义变量m, 先存放键盘上输入的十进制数
3 定义变量R 表示几进制数,循环变量i j
十进制转换成二进制,
就是m不断地除以2,写下每一次除完的余数,能整除就是0,不能就是1。
最后把余数从最后面往前输出,就是二进制数
1 while循环,表示十进制除2取余数的过程,
2 for循环,把余数从后往前输入,输出数组a[i],得到二进制数
【运行结果】
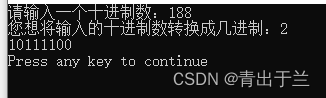
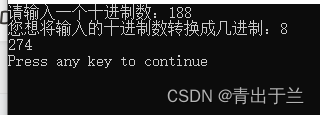
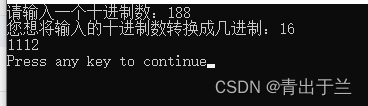
【程序代码】
#include <stdio.h>
int main(void)
{
int a[100] = {0}; //数组初始化,数组元素全部归零
int m = 0; //存储要转换成其他进制的数
int R = 0; // 转换成几进制
int i = 0;
int j = 0;
printf("请输入一个十进制数:");
scanf("%d", &m);
printf("您想将输入的十进制数转换成几进制:");
scanf("%d", &R);
//十进制转二进制:除2取余
while(m)
{
a[i] = m%R; //除2得到的余数,放到数组a中
m /=R; //得到下一次除2取余的数,直到m=0退出循环结束
i++;
}
//因为除2取余,最后要把结果倒过来才是二进制数,所以从后往前输出。
//又因为i最后多加了一次,所以从i-1开始。
for(j=i-1; j>=0; j--)
{
printf("%d", a[j]);
}
printf("\n");
return 0;
}
相关文章:

C语言|十进制数转换任意进制数
将十进制数转换成任意进制数。 思路分析: 先举一个具体的例子:十进制转换为二进制数 1 定义一个数组a[100],先归0,再存放运算过程中的余数 2 定义变量m, 先存放键盘上输入的十进制数 3 定义变量R 表示几进制数,循环变量…...
驱动开发(二):创建字符设备驱动
往期文章: 驱动开发(一):驱动代码的基本框架 驱动开发(二):创建字符设备驱动 ←本文 目录 字符驱动设备的作用 函数 字符驱动设备注册和注销 注册 注销 自动创建设备节点 创建class类…...

Golang:使用时会遇到的错误及解决方法详解
Go语言使用时常常会遇到的一些错误及解决方法,文中的示例代码讲解详细,感兴趣的小伙伴可以了解一下 1、go: go.mod file not found in current directory or any parent directory go mod init name 2、Failed to build the application: main.go:4:2:…...
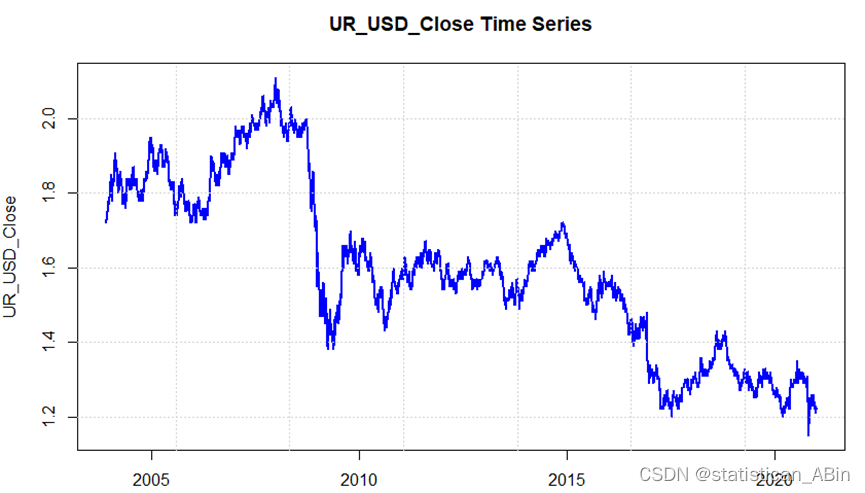
r语言数据分析案例25-基于向量自回归模型的标准普尔 500 指数长期预测与机制分析
一、背景介绍 2007 年的全球经济危机深刻改变了世界经济格局,引发了一系列连锁反应,波及各大洲。经济增长停滞不前,甚至在某些情况下出现负增长,给出口导向型发展中国家带来了不确定性。实体经济受到的冲击尤为严重,生…...
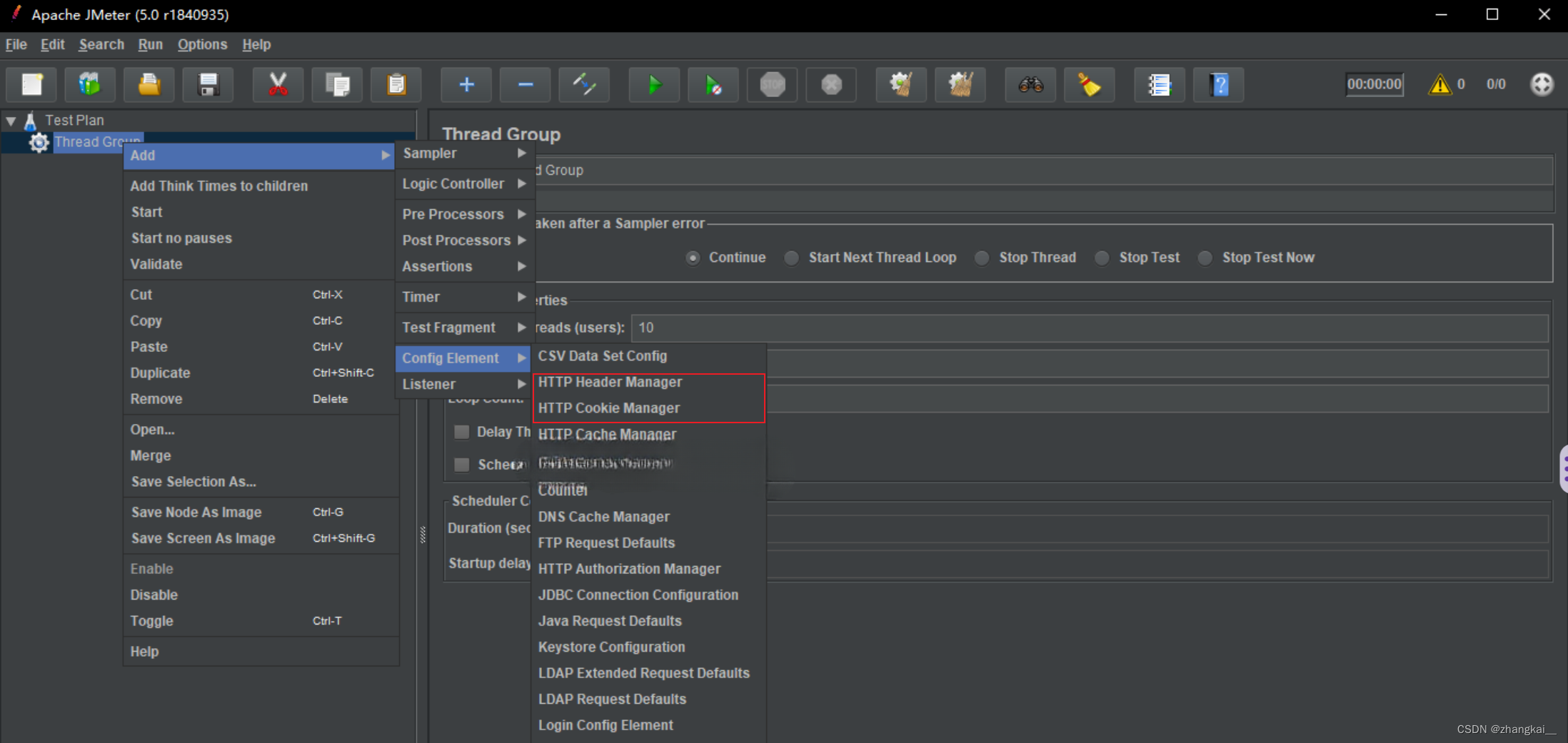
解决使用Jmeter进行测试时出现“302“,‘‘401“等用户未登录的问题
使用 JMeter 压力测试时解决登录问题的两种方法 在使用 JMeter 进行压力测试时,可能会遇程序存在安全验证,必须登录后才能对里面的具体方法进行测试: 如果遇到登录问题,通常是因为 JMeter 无法模拟用户的登录状态,导…...

MySql通过 Procedure 循环删除数据
一、问题描述 在日常使用运维中,一些特殊情况需要批量删除陈旧或异常数据。 如果通过 delete from 【表名】 where 【条件】 直接删除,可能会由于数据量过大,事务执行时间过长,造成死锁。 二、解决方案 通过 Procedure 使用循环…...

Spring Boot 的启动原理、Spring Boot 自动配置原理
Spring Boot启动原理包含自动装配原理。 Spring Boot 的启动原理: 1. 入口类与 SpringApplication 初始化: 应用程序通常从一个带有 SpringBootApplication 注解的主类开始,这个注解是一个组合注解,包含了 SpringBootConfigurat…...

不会开发的你也能管理好企业漏洞,开源免费工具:洞察(insight II)
公司刚开始建设安全管理时,都是从一片混沌开始的,资源总是不够的,我们每个做安全的人员,又要会渗透,又要抓制度,还得管理各种漏洞。在管理楼栋是,我相信大家都遇到过以下几个问题: …...

java实现两个不同对象的集合复制
场景: 我们开发中会遇到集合对象复制的场景,可以避免代码的重复编写 基于 com.alibaba.fastjson.JSON 实现对象集合的拷贝 对象定义:ObjectA属性:id,name,ageObjectB属性:id,name…...

bind failed: Address already in use
添加代码 这是个很常见的问题:在bind函数之前添加如下代码即可。 int yes 1; if (setsockopt(sockfd, SOL_SOCKET, SO_REUSEADDR, &yes, sizeof(int)) -1) { perror("setsockopt"); exit(1); } 查看端口 如果还是不能结果,那么说…...
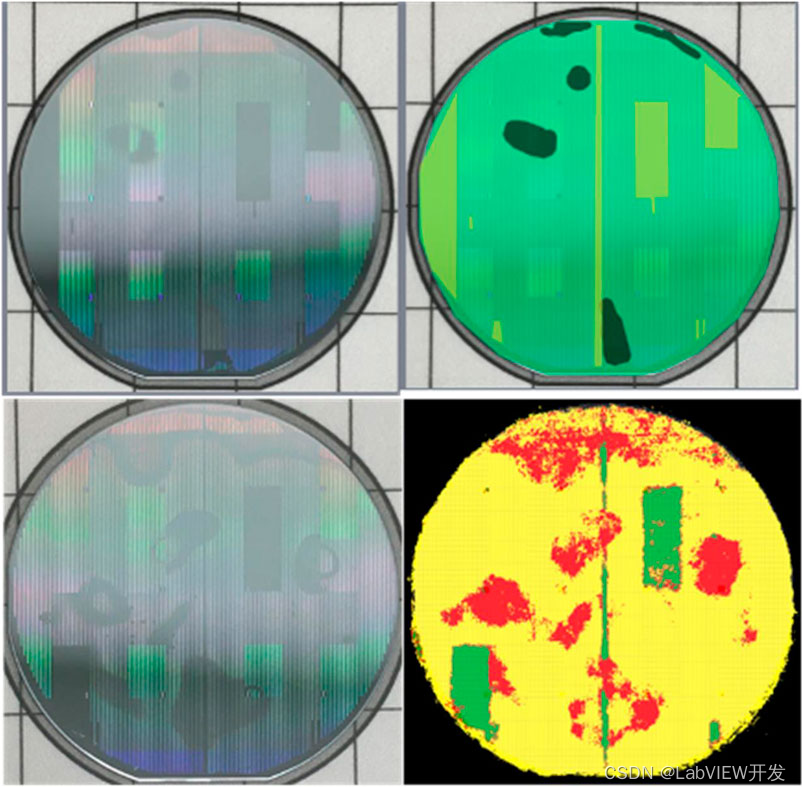
LabVIEW结构体内部缺陷振动检测
结构体内部缺陷会改变其振动特性,通过振动分析可以检测并定位这些缺陷。本文详细分析内部缺陷对振动的影响,从频谱分析、时域分析和模态分析等多角度探讨基于LabVIEW的检测方法,提供实施步骤和注意事项,帮助工程师有效利用LabVIEW…...
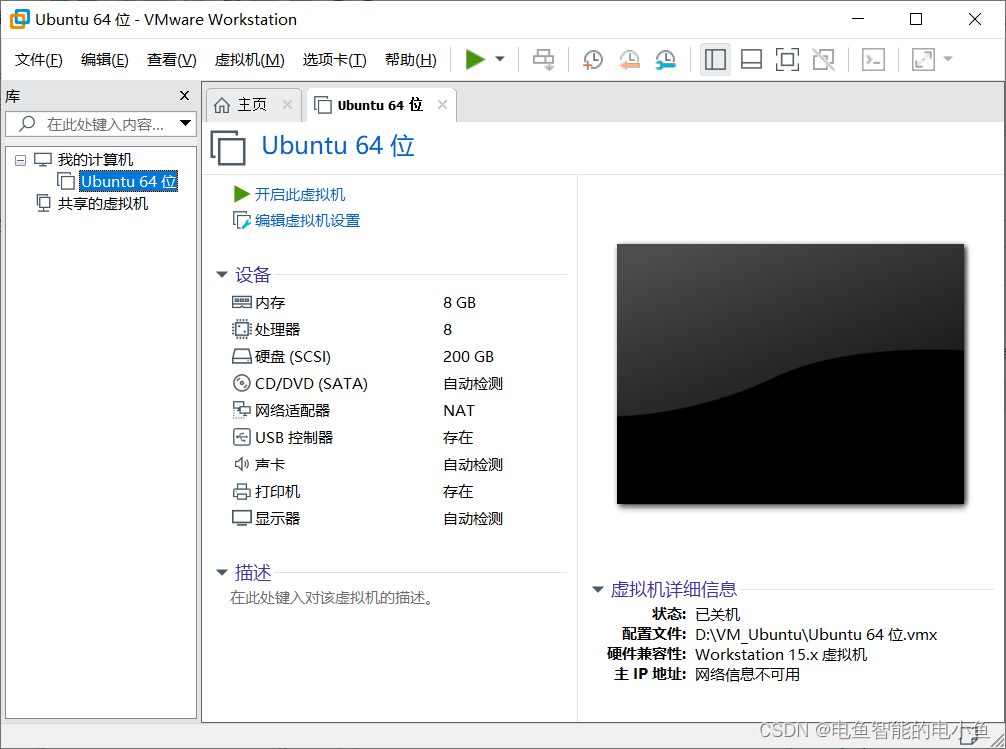
RK3568技术笔记六 新建 Ubuntu Linux 虚拟机
VMware 安装完成后,启动 VMware 软件。启动后在 VMware 主界面点击“创建新的虚拟机”。如下图所示: 开始对新建的虚拟机进行设置。选择“自定义”,然后点击“下一步”。如下图所示: 使用默认配置,单击“下一步”。如下…...

Web前端博客模板下载:一站式解决方案与深度探索
Web前端博客模板下载:一站式解决方案与深度探索 在当今数字化时代,拥有一个美观且功能强大的博客网站已成为许多人的追求。而Web前端博客模板作为构建博客网站的重要工具,其选择和下载对于实现这一目标至关重要。本文将从四个方面、五个方面…...
Docker部署常见应用之大数据实时计算引擎Flink
文章目录 Flink 简介Docker 部署Docker Compose 部署参考文章 Flink 简介 Apache Flink 是一个开源的分布式流批一体化的计算框架,它提供了一个流计算引擎,能够处理有界和无界的数据流。Flink 的核心优势在于其高吞吐量、低延迟的处理能力,以…...

python使用os.getcwd()获取当前路径不正确
# codinggbk import ostry:current_dir os.getcwd()#print(os.path.dirname(os.path.realpath(__file__)))#获取错误print("当前工作目录[不想要]:",current_dir)#获取真实文件夹路径print("当前工作目录[想要]:",os.path.dirname(…...

pycharm终端pip安装模块成功但还是显示找不到 ModuleNotFoundError: No module named
报错信息: ModuleNotFoundError: No module named 但是分明已经安装过此模块: 在cmd运行pip list 查看所有安装过的包找到了安装过: 如果重新安装就是这样:显示已经存在了 问题排查: 直接根据重新安装的显示已存在的…...
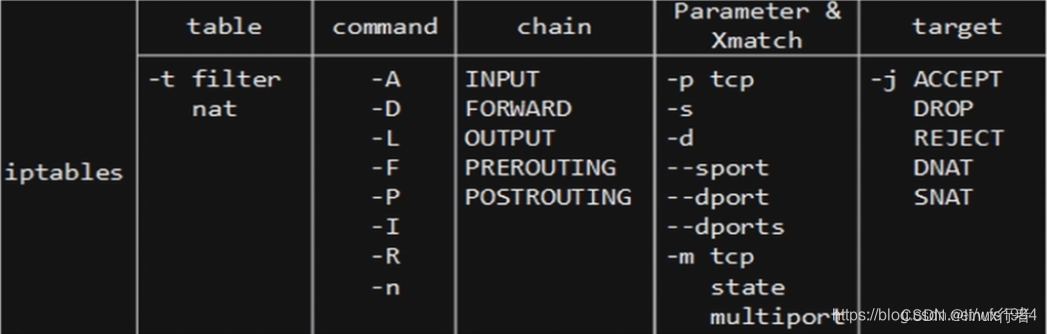
iptables教程
1 iptables安装 1.1 iptables和iptables-service的关系 iptables 是基于内核的,和 iptables-services 没有关系,不用安装任何工具包就可以使用 iptable 命令添加的防火墙规则, 但是iptables添加的规则是临时的,基于内存的&…...

破局外贸企业海外通邮难题,U-Mail邮件中继有绝招
在当今全球化的商业环境中,国内企业正扮演着越来越重要的角色,它们不仅在国内市场活跃,而且在全球范围内拓展业务,成为国际贸易中不可或缺的一部分。然而,尽管这些企业在业务扩展上取得了显著成就,但在与海…...
: 从理论到实践的指南(2))
支持向量机(SVM): 从理论到实践的指南(2)
葡萄酒数据集经常被用于机器学习、模式识别和统计分类算法的测试中。由于其特征维度较高,非常适合于验证特征选择和降维方法,例如主成分分析(PCA)或线性判别分析(LDA)的效果。同时,由于数据集包…...
——修订注释(Redaction))
PDF格式分析(八十六)——修订注释(Redaction)
修订注释(PDF 1.7及其以上版本),该注释的做用是标识要从文档中删除的内容。 修订注释启用的步骤如下: 1、内容标识。PDF编辑器可指定应删除的文档内容片段或区域,在执行下一个步骤前,用户可以看到、移动和重新定义这些注释。 2、内容移除。PDF阅读器应删除修订注释指…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
