北航数据结构与程序设计第五次作业选填题复习
选填题考的很多都是基础概念,对于巩固复习一些仡佬拐角的知识点是很有用的。非北航学生也可以来看看这些题,这一节主要是树方面的习题:
一、
 我们首先需要知道一个公式
我们首先需要知道一个公式

这是证明:

知道了这个公式,我们把题目中的数据带入即可:
n0=n2+2n3+3n4+1
=1+2 * 10+3 * 20+1
=82
二、

两个知识点:
1、二叉树的分支个数等于节点个数-1,适用于任何二叉树,则m=n-1
2、满二叉树的深度与结点个数之间的关系:n=2^h-1 , h=log(n+1)。
因此选D很明显
三、
 这个题蛮有意思,正着想不太好想,那我们就把每个选项都试一试,看看哪个符合要求。
这个题蛮有意思,正着想不太好想,那我们就把每个选项都试一试,看看哪个符合要求。
A.空和仅有一个节点,前序遍历和后序遍历长得一样,要说相反好像勉强也行。这个选项暂时保留,大概率肯定不是,我们往下看。
B.我们画个图实际演示一下
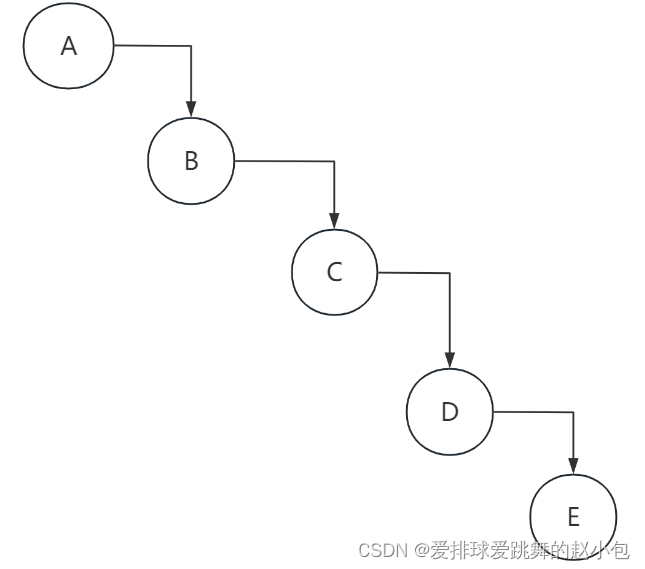 前序遍历:A B C D E
前序遍历:A B C D E
后序遍历:E D C B A
诶好像可以诶!!但是别高兴太早了,我们发现D选项囊括了B选项,那我们就要思考一下,这种情况会不会不全面呢?
C.其实有了上一个题的疑问,我们实际可以直接先验证D选项:
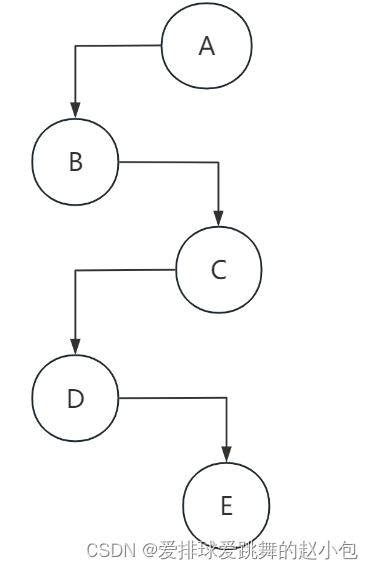
这是一个分支节点的度都为1的树,我们来验证一下他的前后序遍历:
前序遍历:A B C D E
后序遍历:E D C B A
正好相反,因此,正确答案为D
四、
 这道题的正确答案应该是A。
这道题的正确答案应该是A。
二叉查找树的查找效率由平均查找长度(ASL)来决定:

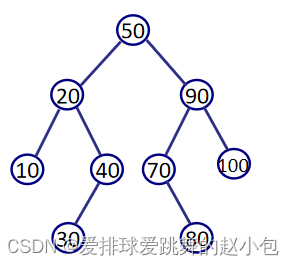
查找第一层的元素,需要比较1次,查找第二层的元素,需要比较2次……查找第n层的元素,需要查找n次,那么上述树的平均查找长度就为:(1 * 1 + 2 * 2 + 3 * 4 + 4 * 2)/9=25/9
在来看时间复杂度:理想情况下,查找一个元素需要比较的最多次数为深度次,也就是从树冠比到树根,那么时间复杂度就是O(h),h=logn (我们这里只说数量级,不考虑具体是满二叉树还是完全二叉树还是普通二叉树),时间复杂度也可以表示为:O(logn)。也就是说,二叉查找树查找的时间复杂度是由深度决定的。
注意,当二叉查找树退化时,也就是说,差不多快变成一个链表的时候(左右子树深度之差过大),那么这个时候查找的时间复杂度就和在链表里查找的时间复杂度差不多了,就变成O(n)了。
六、

这道题的正确答案应该为D
但是我对此存疑,我再问问助教去……
七、

中缀转前缀的方法为:
-
从右到左扫描表达式
-
遇到操作数直接输出,输出顺序从右到左
-
遇到操作符:
1.遇到 ‘ )’,入栈
2.操作符栈空,入栈
3.当前操作符优先级 >= 栈顶操作符,入栈(注意,中缀转后缀是要大于才入栈)
4.当前操作符优先级 < 栈顶操作符,栈顶操作符出栈,然后与新的栈顶元素比较,直到栈空或优先级大于等于栈顶操作符或遇到‘ )’ 时,入栈。 -
遇到括号:
1.遇到右括号,入栈
2.遇到左括号,将栈内运算符依次弹出并从右到左输出,直到遇到左括号,左括号弹出,但左括号不输出 -
将栈内剩余操作符从右到左依次弹出并输出
八、

前缀编码,任何一个编码都不能成为其他编码的前缀,但是B中,10是101的前缀。
九、

先来了解一下哈夫曼树的构造原理:
1.树的带权路径长度WPL:

wi为第i个叶结点被赋予的权值,li为根节点到第i个叶结点的路径长度
2.哈夫曼树的定义:
给定一组权值,构造出的具有最小带权路径长度的二叉树即哈夫曼树
3.哈夫曼树特点:
-
权值越大,离根越近,权值越小,离根越小
-
无度为1的节点
-
哈夫曼树不唯一
4.哈夫曼树的构造
- 对于给定的权值W={w1,w2,…… ,wm},构造出树林F={T1,T2,…… ,Tm},其中Ti为左右子树为空,且根节点的权值为wi的二叉树
- 将F中根节点权值最小的两棵二叉树合并成为一棵新的二叉树,将这两棵二叉树作为新二叉树的左右子树,并将新二叉树的根结点的权值定为这两棵二叉树权值的和。将新二叉树加入F,同时从F中删除之前的两棵二叉树
- 重复上一步,直到F中只有一棵二叉树。
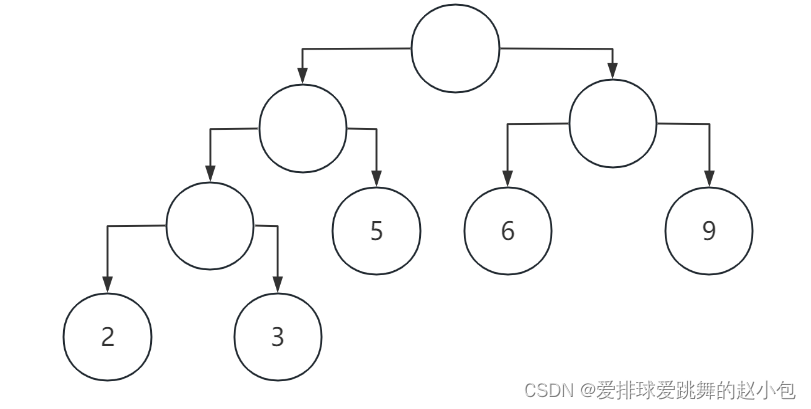
按照上述步骤,我们构造出了一棵哈夫曼树,那么带权路径长度就为:
2 * 3 + 3 * 3 + 5 * 2 + 6 * 2 + 9 * 2 = 55
二、

度为k,那么要求最多个结点,我们就让每个分支节点的度都为K,那么第一层就有k^0个结点,
第二层有k^1个,
第三层:k^2,
第四层:k^3,
以此类推,第i层最多就有k^(i-1)个节点
三、

满二叉树的深度和结点个数关系:n=2^h-1,则h=log(n+1),可得深度为:log(2048)=11,最后一层的节点个数,也就是叶结点个数为n=2 ^ (h-1)=2 ^ 10 = 1024。
四、
 先恢复一下二叉树:
先恢复一下二叉树:
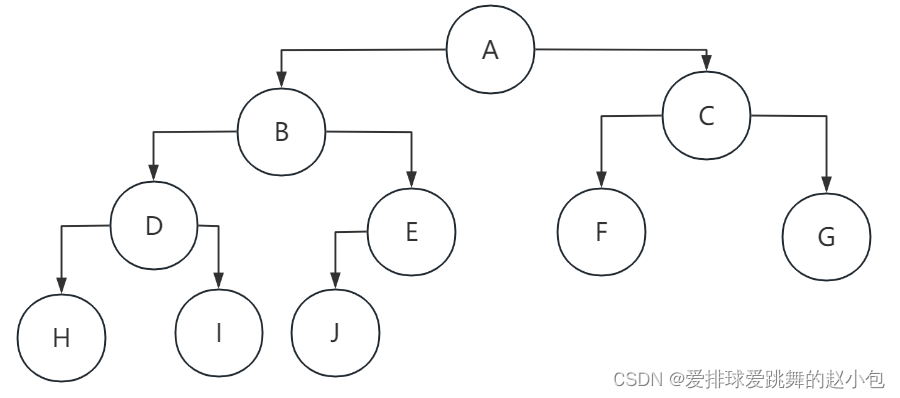
那么后续序列就为:
HIDJEBFGCA
五、

每个结点都有left和right两个指针,因此共有2n个指针域
分支节点个数等于节点个数减一,那么就意味着n-1个指针指向孩子节点,剩下的2n-(n-1)=n+1个指针域就指向空
六、
 先恢复一下二叉树
先恢复一下二叉树
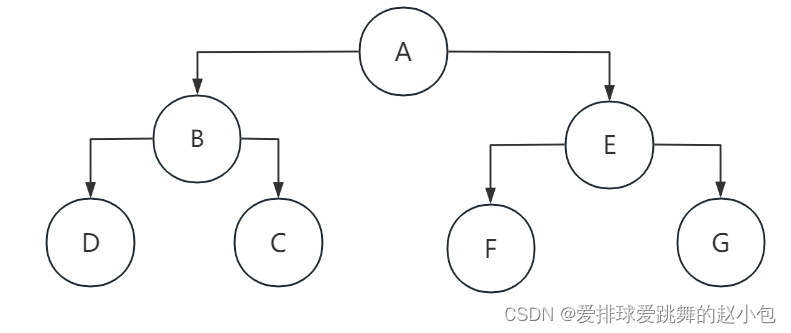
那么后序遍历结果就是:DCBFGEA
七、
 处在同一层,说明深度一样,
处在同一层,说明深度一样,
2^ (h-1) - 1 < i < 2 ^ (h) - 1
2^ (h-1) - 1 < j < 2 ^ (h) - 1
八、

这个注意,做减法和除法的时候,先弹出的减(除)后弹出的,和后缀表达式计算不太一样。
九、
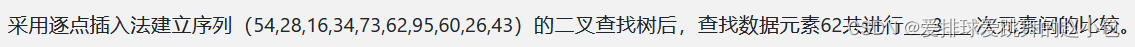
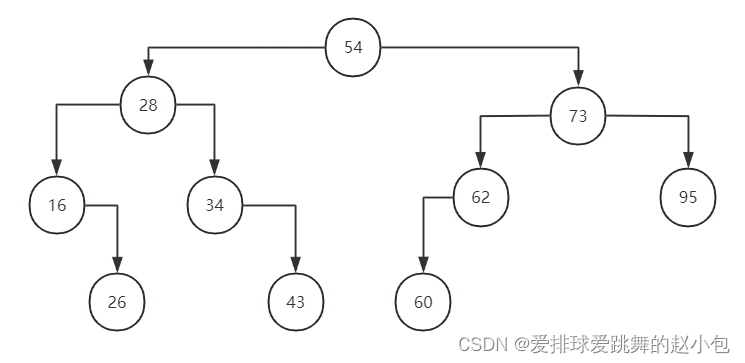
建立好的二叉查找树如上图,62先和54比,再和73比,再和62比,发现找到,结束比较,工比较三次。
十、

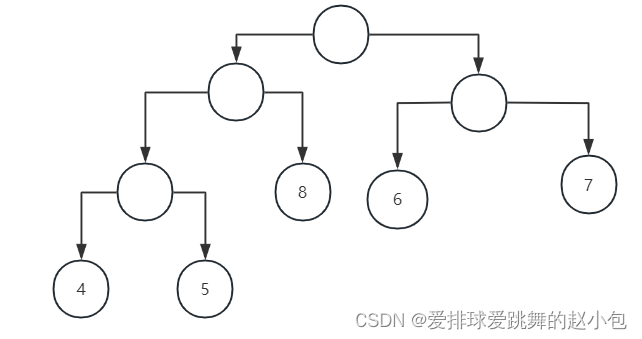
则带权路径长度为:4×3+5×3+8×2+6×2+7×2=12+15+16+12+14=69
相关文章:

北航数据结构与程序设计第五次作业选填题复习
选填题考的很多都是基础概念,对于巩固复习一些仡佬拐角的知识点是很有用的。非北航学生也可以来看看这些题,这一节主要是树方面的习题: 一、 我们首先需要知道一个公式 这是证明: 知道了这个公式,我们把题目中的数据…...
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第40课-实时订阅后端数据
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第40课-实时订阅后端数据 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。dtns.network是一款主要由JavaScript编写的智体世界引…...

系统集成知识科普:核心原理与关键技术
目录 1.系统集成的核心原理 1.1 模块化原理 1.1.1 定义: 1.1.2 优势: 1.1.3 实现方式: 1.2 标准化原理 1.2.1 定义: 1.2.2 作用: 1.2.3 实践案例: 1.2.4 制定与遵循: 1.3 协同性原理…...

Coze+Discord:打造你的免费AI助手(教您如何免费使用GPT-4o/Gemini等最新最强的大模型/Discord如何正确连接Coze)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 文章内容 📒📝 准备Discord📝 准备Coze🔌 连接💡 测试效果⚓️ 相关链接 ⚓️📖 介绍 📖 你是否想免费使用GPT-4o/Gemini等最新最强的大模型,但又不想花费高昂的费用?本文将教你如何通过Coze搭建Bot,并将其转发…...

「OC」UI练习(二)——照片墙
「OC」UI练习——照片墙 文章目录 「OC」UI练习——照片墙UITapGestureRecognizer介绍照片墙实现 UITapGestureRecognizer介绍 UITapGestureRecognizer是UIKit框架中的一个手势识别器类,用于检测用户在视图上的轻击手势。它是UIGestureRecognizer的一个子类&#x…...

一手洞悉巴西slot游戏包投放本土网盟CPI广告优势
一手洞悉巴西slot游戏包投放本土网盟CPI广告优势 在巴西这片热土上,slot游戏包的投放本土网盟CPI广告是一项既充满挑战又富有机遇的任务。CPI(Cost Per Install)广告模式,即按安装付费,已经成为许多游戏开发商推广产品…...

中国环保网引领元宇宙新纪元 -探索绿色未来
在数字化浪潮的推动下,元宇宙这一概念正逐渐进入公众视野,成为科技与创新交汇的新前沿。作为环境保护的坚定倡导者,中国环保网秉承着推动绿色发展、构建生态文明的使命,正式踏入元宇宙领域,旨在通过高科技手段为环保事…...

2024最新流媒体在线音乐系统网站源码 音乐社区 多语言开心版
本文来自:2024最新流媒体在线音乐系统网站源码 音乐社区 多语言开心版 - 源码1688 应用介绍 简介: 2024最新流媒体在线音乐系统网站源码| 音乐社区 | 多语言 | 开心版 图片:...

【Java】解决Java报错:FileNotFoundException
文章目录 引言1. 错误详解2. 常见的出错场景2.1 文件路径错误2.2 文件名拼写错误2.3 文件权限问题2.4 文件路径未正确拼接 3. 解决方案3.1 检查文件路径3.2 使用相对路径和类路径3.3 检查文件权限3.4 使用文件选择器 4. 预防措施4.1 使用配置文件4.2 使用日志记录4.3 使用单元测…...

Seate分布式锁
XA模式 在第一阶段资源协调者(TC)会向资源管理者(RM)发出一个准备的请求,RM开始处理自身的业务,处理完成后不提交事务,而是向TC响应一个执行结果,表明自己成功还是失败,如…...

金融科技助力绿色金融:可持续发展新动力
随着全球气候变化和环境问题的日益严重,绿色金融作为推动环境保护和经济可持续发展的重要手段,已经受到越来越多的关注。而金融科技,作为科技与金融深度融合的产物,正以其独特的优势为绿色金融的发展注入新动力。本文将探讨金融科…...

灾备建设中虚拟机细粒度恢复的含义及技术使用
灾备建设中为了考虑虚拟机恢复的效率与实际的用途,在恢复上出了普通的恢复虚拟机,也有其余的恢复功能,比如瞬时恢复,细粒度恢复等。这里谈的就是细粒度恢复。 首先细粒度恢复是什么,这个恢复可以恢复单个备份下来的文…...

十种排序方法
目录 1.冒泡排序(Bubble Sort)代码实现 2.选择排序(Selection Sort)代码实现 3.插入排序(Insertion Sort) 4.希尔排序(Shell Sort)代码实现 5.快速排序(Quick Sort&…...
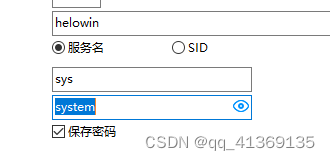
docker-compose启动oracle11、并使用navicat进行连接
一、docker-compose.yml version: 3.9 services:oracle:image: registry.cn-hangzhou.aliyuncs.com/helowin/oracle_11grestart: alwaysprivileged: truecontainer_name: oracle11gvolumes:- ./data:/u01/app/oracleports:- 1521:1521network_mode: "host"logging:d…...

使用ffmpeg进行音频处理
音频处理是数字媒体制作中不可或缺的一部分,而ffmpeg作为一款强大的多媒体处理工具,为我们提供了丰富的音频处理功能。 一、查看音频信息 在处理音频之前,了解音频的基本信息是非常重要的。FFmpeg的ffprobe工具可以帮助我们查看音频的详细信息,如采样率、位深等。 示例命…...

重装系统,以及设置 深度 学习环境
因为联想y7000在ubantu系统上连不到wifi,所以打算弄双系统 第一步:下载win10镜像,之后在系统用gparted新建个分区,格式化成ntfs,用来装win10系统 第二步,制作win10启动盘,这个需要先把u盘用disks格式化&a…...

深入理解渲染引擎:打造逼真图像的关键
在数字世界中,图像渲染是创造逼真视觉效果的核心技术。渲染引擎,作为这一过程中的关键组件,负责将二维或三维的模型、纹理、光照等数据转化为人们肉眼可见的二维图像。本文将深入探讨渲染引擎的工作原理及其在打造逼真图像中所起的关键作用。…...

【LeetCode最详尽解答】128_最长连续序列 Longest-Consecutive-Sequence
欢迎收藏Star我的Machine Learning Blog:https://github.com/purepisces/Wenqing-Machine_Learning_Blog。如果收藏star, 有问题可以随时与我交流, 谢谢大家! 链接: 128_最长连续序列 直觉 输入: nums [100, 4, 200, 1, 3, 2]输出: 4解释: 最长的连续元素序列是…...
盒马鲜生礼品卡如何使用?
盒马鲜生的礼品卡除了在门店用以外,还有什么用处啊 毕竟家附近的盒马距离都太远了,好多卡最后都闲置下来了,而且以前都不知道盒马卡还会过期,浪费了好多 还好最近发现了 盒马鲜生礼品卡现在也能在收卡云上兑现了,而且…...

有哪些常用ORM框架
ORM(Object-Relational Mapping,对象关系映射)是一种编程技术,它允许开发者使用面向对象的编程语言来操作关系型数据库。ORM的主要目的是将数据库中的数据表映射到编程语言中的对象,从而使得开发者可以使用对象的方式来…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
