前缀和算法:算法秘籍下的数据预言家
✨✨✨学习的道路很枯燥,希望我们能并肩走下来!
文章目录
目录
文章目录
前言
一. 前缀和算法的介绍
二、前缀和例题
2.1 【模版】前缀和
2.2 【模板】二维前缀和
2.3 寻找数组的中间下标
2.4 除自身以外数组的乘积
2.5 和为k的子数组
2.6 和可被k整除的子数组
2.7 连续数组
2.8 矩阵区域和
总结
前言
本篇详细介绍了前缀和算法的使用,让使用者了解前缀和,而不是仅仅停留在表面, 文章可能出现错误,如有请在评论区指正,让我们一起交流,共同进步!
一. 前缀和算法的介绍
前缀和算法是一种用空间换时间的算法,他常常用于解决某些题目或者作为某些高级算法的组成部分。
例如:让你求某个矩阵(一维)的子矩阵的最大值,如果使用暴力解法它的时间复杂度将会是O(n^2) ,但如果使用该算法就可以使其时间复杂度降低一个维度也就是O(N).
前缀和 是从 nums 数组中的第 0 位置开始累加,到第 𝑖位置的累加结果,我们常把这个结果保存到数组 Sum 中,记为 Sum[i]。
前缀和算法的本质是一个简单动态规划
接下来我们使用一些例题来介绍一下
二、前缀和例题
2.1 【模版】前缀和
牛客网—【模版】前缀和


#include <iostream>
#include<vector>
using namespace std;int main() {//1.读入数据int n ,q;cin>>n>>q;vector<int> arr(n+1);for(int i = 1;i<=n;i++) cin>>arr[i];//2. 预处理出来个前缀和数组vector<long long> dp(n+1); //防止溢出for(int i = 1;i<=n;i++) dp[i] = dp[i-1]+arr[i];//3.使用前缀和数组int l = 0, r = 0;while(q--){cin>>l>>r;cout<<dp[r]-dp[l-1]<<endl;}return 0;}2.2 【模板】二维前缀和
牛客网—【模版】二维前缀和


#include <iostream>
#include <vector>
using namespace std;int main() {int n,m,q;cin>>n>>m>>q;vector<vector<int>> arr(n+1,vector<int>(m+1));for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){cin>>arr[i][j];}}vector<vector<long long>> dp(n+1,vector<long long>(m+1));for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];}}int x1 = 0,y1 = 0,x2 = 0 ,y2 = 0;while(q--){cin>>x1>>y1>>x2>>y2;cout<<dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]<<endl;}return 0;
}2.3 寻找数组的中间下标
724. 寻找数组的中心下标 - 力扣(LeetCode)


class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);//1. 预处理前缀和数组和后缀和数组for(int i = 1;i<n;i++)f[i] = f[i-1] + nums[i-1];for(int i = n-2;i>=0;i--)g[i] = g[i+1] + nums[i+1];//2. 使用for(int i = 0;i<n;i++)if(f[i] == g[i]) return i;return -1;}
};2.4 除自身以外数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode)


class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();//细节处理vector<int> f(n,1), g(n,1);//前缀和和后缀和for(int i = 1;i<n;i++)f[i] = f[i-1]*nums[i-1];for(int i = n-2;i>=0;i--)g[i] = g[i+1]*nums[i+1];//使用vector<int> ret(n);for(int i = 0;i<n;i++)ret[i] = f[i] * g[i];return ret;}
};2.5 和为k的子数组
560. 和为 K 的子数组 - 力扣(LeetCode)


class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int> hash; //统计前缀和出现的次数hash[0] = 1;int sum = 0, ret = 0;for(auto&x : nums){sum+=x; //计算当前位置的前缀和if(hash.count(sum-k)) ret+=hash[sum-k]; //统计个数hash[sum]++;}return ret;}
};2.6 和可被k整除的子数组
974. 和可被 K 整除的子数组 - 力扣(LeetCode)


class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int> hash;hash[0 % k] = 1; //0 这个数的余数int sum = 0, ret = 0;for(auto& x : nums){sum+=x; //算出当前位置的前缀和if(hash.count((sum%k+k)%k)) ret+=hash[(sum%k+k)%k]; //修正后的余数+统计结果hash[(sum%k+k)%k]++;}return ret;}
};2.7 连续数组
525. 连续数组 - 力扣(LeetCode)

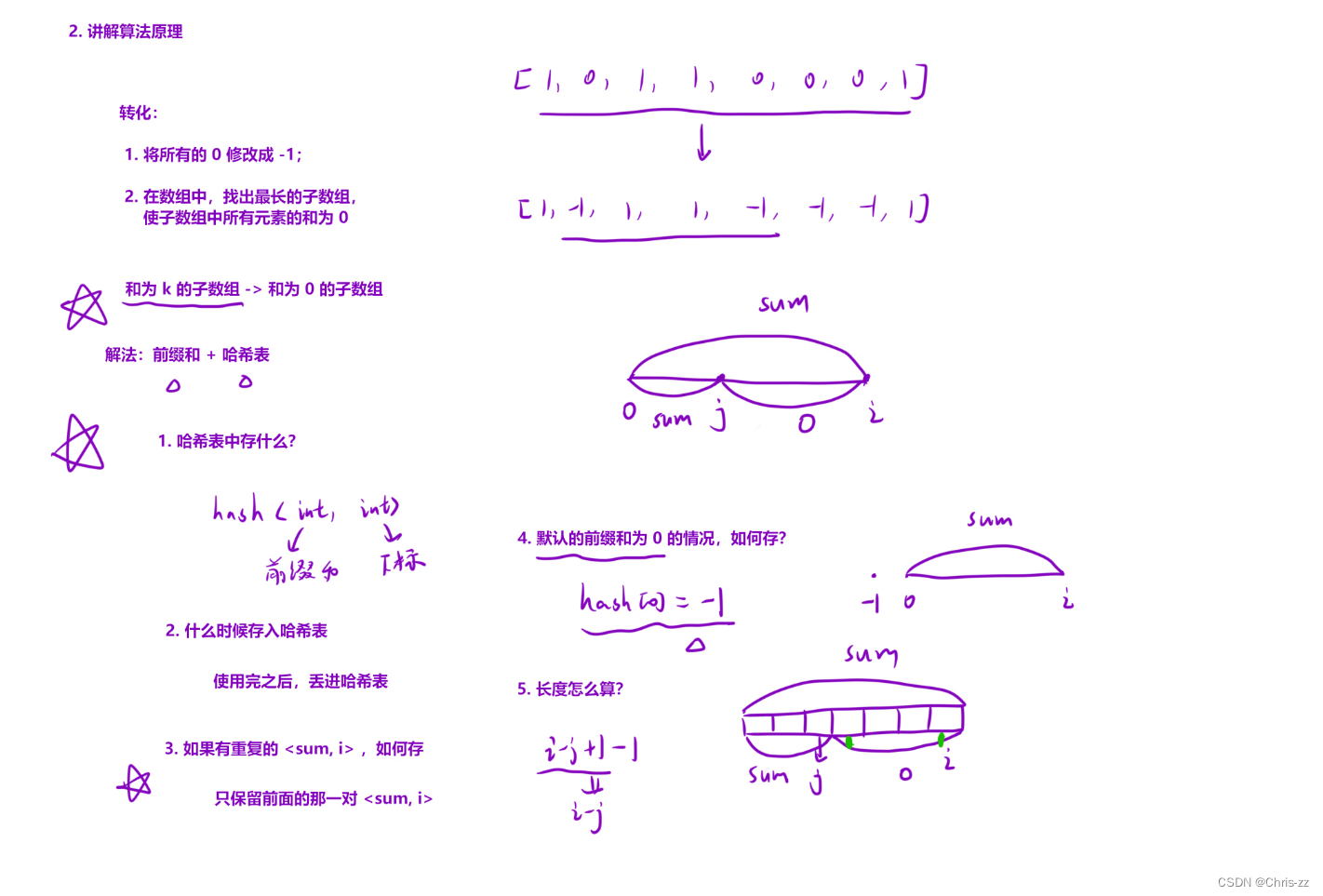
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int> hash;hash[0] = -1; //默认有一个前缀和为0的情况int sum = 0, ret = 0;for(int i = 0;i<nums.size();i++){sum+=nums[i] == 0 ? -1 : 1; //计算当前位置的前缀和if(hash.count(sum)) ret = max(ret,i - hash[sum]);else hash[sum] = i;}return ret;}
};2.8 矩阵区域和
1314. 矩阵区域和 - 力扣(LeetCode)
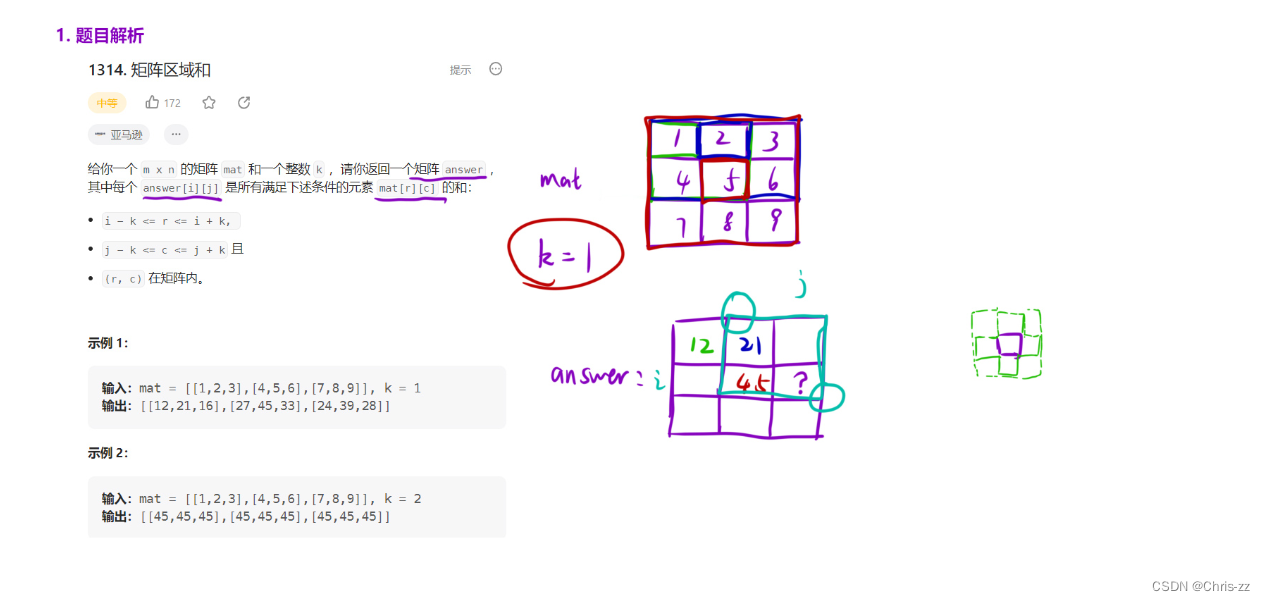

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1;i<=m;i++)for(int j = 1;j<=n;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];vector<vector<int>> answer(m,vector<int>(n));for(int i = 0;i<m;i++)for(int j = 0;j<n;j++){int x1 = max(0,i-k)+1;int y1 = max(0,j-k)+1;int x2 = min(m-1,i+k)+1;int y2 = min(n-1,j+k)+1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];}return answer;}
};总结
✨✨✨各位读友,本篇分享到内容是否更好的让你理解前缀和算法,如果对你有帮助给个👍赞鼓励一下吧!!
🎉🎉🎉世上没有绝望的处境,只有对处境绝望的人。
感谢每一位一起走到这的伙伴,我们可以一起交流进步!!!一起加油吧!!
相关文章:

前缀和算法:算法秘籍下的数据预言家
✨✨✨学习的道路很枯燥,希望我们能并肩走下来! 文章目录 目录 文章目录 前言 一. 前缀和算法的介绍 二、前缀和例题 2.1 【模版】前缀和 2.2 【模板】二维前缀和 2.3 寻找数组的中间下标 2.4 除自身以外数组的乘积 2.5 和为k的子数组 2.6 和可被k整除的子数组 2.7 …...

基于PointNet / PointNet++深度学习模型的激光点云语义分割
一、场景要素语义分割部分的文献阅读笔记 1.1 PointNet PointNet网络模型开创性地实现了直接将点云数据作为输入的高效深度学习方法(端到端学习)。最大池化层、全局信息聚合结构以及联合对齐结构是该网络模型的三大关键模块,最大池化层解决了…...

LabVIEW调用DLL时需注意的问题
在LabVIEW中调用DLL(动态链接库)是实现与外部代码集成的一种强大方式,但也存在一些常见的陷阱和复杂性。本文将从参数传递、数据类型匹配、内存管理、线程安全、调试和错误处理等多个角度详细介绍LabVIEW调用DLL时需要注意的问题,…...

时序预测 | MATLAB实现TCN-Attention自注意力机制结合时间卷积神经网络时间序列预测
时序预测 | MATLAB实现TCN-Attention自注意力机制结合时间卷积神经网络时间序列预测 目录 时序预测 | MATLAB实现TCN-Attention自注意力机制结合时间卷积神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.MATLAB实现TCN-Attention自注意力机制结合时…...
上位机图像处理和嵌入式模块部署(h750 mcu vs f407)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 在目前工业控制上面,f103和f407是用的最多的两种stm32 mcu。前者频率低一点,功能少一点,一般用在低端的嵌入式设…...
Linux C语言:指针和指针变量
一、指针的作用 使程序简洁、紧凑、高效有效地表示复杂的数据结构动态分配内存能直接访问硬件能够方便的处理字符串得到多于一个的函数返回值 二、内存、地址和变量 1、内存地址 2、变量和地址 1)变量用来在程序中保存数据 比如: int k 58; //声明一个int变…...

Llama模型家族之Stanford NLP ReFT源代码探索 (二)Intervention Layers层
LlaMA 3 系列博客 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 基于 LlaMA…...

MATLAB神经网络---序列输入层sequenceInputLayer
序列输入层sequenceInputLayer 描述一: sequenceinputlayer是Matlab深度学习工具箱中的一个层,用于处理序列数据输入。它可以将输入数据转换为序列格式,并将其传递给下一层进行处理。该层通常用于处理文本、语音、时间序列等类型的数据。在使用该层时&…...

使用CSS、JavaScript、jQuery三种方式实现手风琴效果
手风琴效果有不少,王者荣耀官网(源网址 https://pvp.qq.com/raiders/ )有一处周免英雄,使用的就是手风琴效果,如图所示。 我试着用css、js、jQuery三种方式实现了这种效果,最终效果差不多,美中不…...

什么是无头浏览器以及其工作原理?
如果您对这个概念还不熟悉,那么使用无头网络浏览器的想法可能会让您感到不知所措。无头浏览器本质上与您熟悉的网络浏览器相同,但有一个关键区别:它们没有图形用户界面 (GUI)。这意味着没有按钮、选项卡、地址栏或视觉显示。 相反,…...
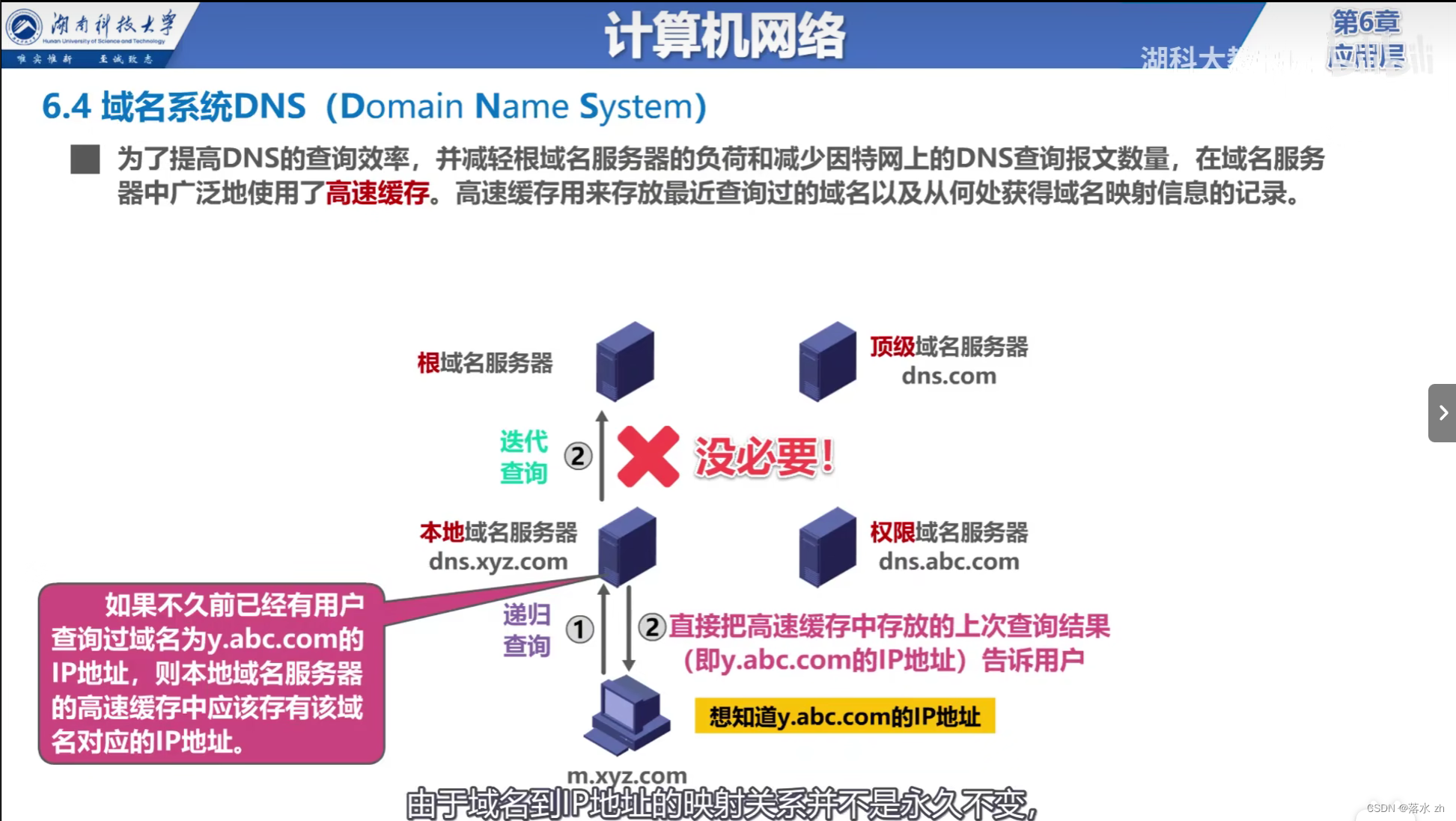
计算机网络 —— 应用层(DNS域名系统)
计算机网络 —— 应用层(DNS域名系统) 什么是DNS域名的层次结构域名分类 域名服务器的分类域名解析方式递归查询(Recursive Query)迭代查询(Iterative Query)域名的高速缓存 我们今天来看DNS域名系统 什么…...
Linux--MQTT简介
一、简介 MQTT ( Message Queuing Telemetry Transport,消息队列遥测传输), 是一种基于客户端服务端架构的发布/订阅模式的消息传输协议。 与 HTTP 协议一样, MQTT 协议也是应用层协议,工作在 TCP/IP 四…...

VMware Workerstation开启虚拟机后,产生乱码名称日志文件
问题情况 如下图所示,我的虚拟机版本是16.1.2版本,每次在启动虚拟机之后,D盘目录下都会产生一个如图下所示的乱码名称文件。同时,虚拟机文件目录也是杂乱不堪,没有按照一台虚拟机对应一个文件夹的形式存在。 问题处理…...

Unity射击游戏开发教程:(27)创建带有百分比的状态栏
创建带有弹药数和推进器百分比的状态栏 在本文中,我将介绍如何创建带有分数和百分比文本的常规状态栏。 由于 Ammo Bar 将成为 UI 的一部分,因此我们需要向 Canvas 添加一个空的 GameObject 并将其重命名为 AmmoBar。我们需要一个文本和两个图像对象,它们是 AmmoBar 的父级。…...
---更新中)
Linux内存从0到1学习笔记(8.16 SMMU详解)---更新中
写在前面 前面博客已经了解过。SMMU是IOMMU在ARM架构上的实现。主要为了解决虚拟化环境中,GuestOS无法直接将连续的物理地址分配给硬件的问题。对于Hypervisor/GuestOS的虚拟化系统来说,所有的VM都运行在Hypervisor上,每一个VM独立运行一个O…...

标准盒模型和怪异盒模型的区别
CSS盒模型: 内容区(content)内边距(padding)边框(border)外边距(margin) 分为标准盒模型和IE盒模型/怪异盒模型 为了正确设置元素在所有浏览器中的宽度和高度…...
ComfyUI基础入门教程)
【第8章】如何利用ControlNet生成“可控画面”?(配置要求/一键安装/快速上手/生成第一张图)ComfyUI基础入门教程
这节我们来讲AI绘画领域中一个很重要的概念:ControlNet,看下如何让生成的画面更可控。 🎅什么是ControlNet? Stable Diffusion中的ControlNet是一种神经网络结构,它允许将额外的条件输入添加到预训练的图像扩散模型中,通过这种方式,ControlNet可以控制图像生成过程,…...
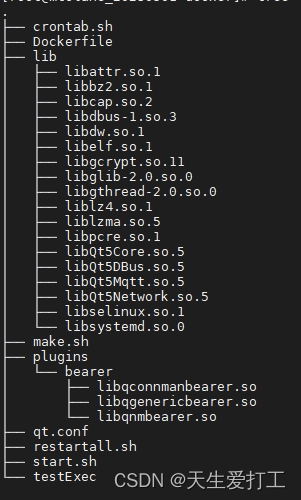
[qt] qt程序打包以及docker镜像打包
目录 一 环境准备: 1.1 qt环境 1.2 linuxdeplouqt打包工具 二 qt包发布: 2.1 搜索链接库 2.2 应用程序APP打包 2.3 发布 三 docker镜像包发布 3.1 环境准备 3.2 镜像生产脚本 3.3 加载镜像并运行docker容器 四 补充 4.1 时间不同步问题解决 一 环境准备: qt环境l…...

电脑屏幕监控软件有哪些?2025年监控软件排行榜
电脑屏幕监控软件有哪些?2025年监控软件排行榜 虽然现在还是2024年,但是有一些被广泛讨论和推荐的电脑屏幕监控软件,它们将在2025年异军突起,成为行业的引领者。 1.安企神软件: 功能全面的电脑屏幕监控软件…...

音视频主要概念
文章目录 常用的一些概念主要概念1主要概念2I帧P帧B帧 常用视频压缩算法 小结 常用的一些概念 主要概念1 视频码率:kb/s,是指视频文件在单位时间内使用的数据流量,也叫码流率。码率越大,说明单位时间内取样率越大,数…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
