【算法-力扣】72. 编辑距离(动态规划)
目录
一、题目描述
二、解题思路
三、参考答案
一、题目描述
编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
二、解题思路
1、首先确定DP数组以及它的含义
这里我们使用一个二维的DP数组dp[i][j],此时dp[i][j]就表示word1和word2对应的i和j位置结束的时候转换后的最少操作次数。比如word1为abc,word2为dcdb,则dp[1][3]就表示ab转换成dcdb的最少转换次数。这个dp[i][j]的含义一定要记住,不然后面再推导递推公式的时候就很容易把自己绕晕!
2、如何初始化dp数组
首先我们要确定,我们要初始化dp数组的哪些位置。因为我们的dp[i][j]表示的是word1和word2对应的i和j位置结束的时候转换后的最少操作次数。所以,最终的我们要的结果也就是dp二维数组的最后一个元素。
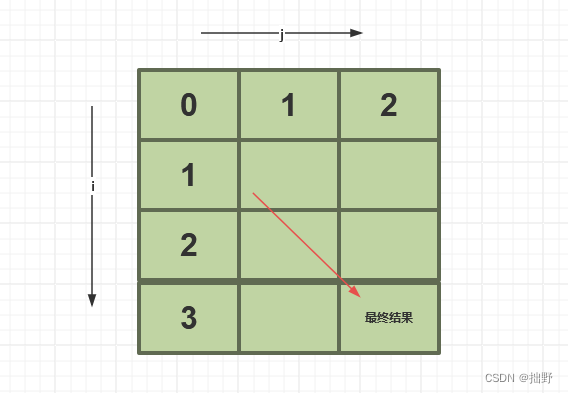
所以,这里我们需要初始化dp数组的第一行和第一列。这样,最终我们才能根据第一行和第一列的数据来推导出来最终的结果。
那么,问题来了,我们该如何初始化第一行和第一列的数据呢?
比如,word1为abc,word2为dcdb。我们初始化第一行的时候,那就是要求出a分别转换成d、dc、dcd、dcdb时的最少操作次数。显然这样初始化是非常麻烦的,甚至是不可完成的!那么我们再假设word1为zabc,word2为zdcdb。此时我们初始化第一行的时候,则就是求z分别转换成z、zd、zdc、zdcd、zdcdb时的最少操作次数。显然这个时候就很简单了对应最少操作次数其实就是j的值。
那么,灵感来了!
我们只要对word1和word2分别在它的首位置都添加一个相同的字符就行了!因为两个字符相同,所以不会影响我们最终的结果的。此时初始化dp数组就如下:
// 初始化第一行for (int j = 0; j < n; j++)dp[0][j] = j;// 初始化第一列for (int i = 0; i < m; i++)dp[i][0] = i;注:m是word1单词的长度,n是word2单词的长度。
3、确定递推公式
- 当前遍历的dp[i][j]对应word1和word2位置上的字符相等的时候
dp[i][j] = dp[i-1][j-1]
此时不需要任何操作,所以此时的 dp[i][j] = dp[i-1][j-1]
- 当前遍历的dp[i][j]对应word1和word2位置上的字符不相等的时候,此时就需要进行操作
1)插入、删除
插入和删除操作是等价的,比如a和ab我们删除b和添加b操作次数都是一样的。所以这里我们只考虑删除即可。删除有可能删除word1的i位置的元素,也有可能删除word2的j位置的元素,删除word1和删除word2对应的操作次数是不一样的,所以需要比较出一个操作次数少的。
删除word1的i位置的元素:dp[i][j] = dp[i-1][j]+1
删除word2的j位置的元素:dp[i][j] = dp[i][j-1]+1
此时在当前操作下的最少操作次数就是:
dp[i][j] = Math.min(dp[i-1][j]+1, dp[i][j-1]+1);
如果此时有点晕,一定要再想dp[i][j]代表的是什么!
2)替换
替换也就是将word1在i位置的字符替换成word2在j位置的字符或者是将word2在j位置的字符替换成word1在i位置的字符。不管它俩谁替换谁,我们最终关心的只是操作次数。所以,这里也就是1次操作。所以,我们只要在它们俩前一个位置上的时的最少操作次数上面加1,也就是word1和word2在当前位置和当前替换操作下的最少操作次数了。
dp[i][j] = dp[i-1][j-1]+1
最后,我们求出这些操作中哪个操作次数最少,也就是我们最终该位置上的最少操作次数了。也就是在word1和word2在i和j位置上的字符不相等的时候的递推公式了。
dp[i][j] = Math.min( dp[i-1][j-1]+1, Math.min(dp[i-1][j]+1, dp[i][j-1]+1));
三、参考答案
class Solution {public int minDistance(String word1, String word2) {// 两个字符串前面都加个空字符串,方便后续初始化二维dp数组word1 = " " + word1;word2 = " " + word2;char[] word1Array = word1.toCharArray();char[] word2Array = word2.toCharArray();int m = word1Array.length, n = word2Array.length;// 定义一个dp二维数组,dp[i][j]表示word1和word2对应的i和j位置的时候最少操作次数int[][] dp = new int[m][n];// 初始化dp数组// 初始化第一行for (int j = 0; j < n; j++)dp[0][j] = j;// 初始化第一列for (int i = 0; i < m; i++)dp[i][0] = i;// 遍历for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {// 当当前位置相等的时候if (word1Array[i] == word2Array[j]) {dp[i][j] = dp[i - 1][j - 1];} else { // 不相等的时候需要处理dp[i][j] = Math.min(Math.min(dp[i][j-1],dp[i-1][j-1]),dp[i-1][j])+1;}}}return dp[m-1][n-1];}
}以上就是使用动态规划解决力扣上72题编辑距离的方法。通过使用动态规划,我们可以高效地解决这个问题,时间复杂度为O(m*n),其中m和n分别是字符串word1和word2的长度。编辑距离是一个非常有意义的问题,掌握了解决方法后,我们就可以将其应用到各种实际问题中,提高算法的效率。编辑距离在我们的实际开发中有很多的应用场景,比如拼写纠错、数据对齐、抄袭侦测等。
相关文章:

【算法-力扣】72. 编辑距离(动态规划)
目录 一、题目描述 二、解题思路 三、参考答案 一、题目描述 编辑距离 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符 删除一个字符 替换一个字符 示例 1&#…...

Spring 系统架构图
Spring 系统架构图 Spring Framework是Spring生态圈中最基础的项目,是其他项目的根基。 Spring Framework的发展也经历了很多版本的变更,每个版本都有相应的调整 Spring Framework的5版本目前没有最新的架构图,而最新的是4版本,…...

同三维T80005EHS-4K60 4K60 HDMI/SDI编码器
1路4K60 HDMI或12G SDI输入,2路3.5MM音频输入,对应HDMI或SDI,1个USB口和1个SD卡槽,可录像到U盘/移动硬盘/SSD硬盘/TF卡 产品简介: 同三维T80005EHS-4K60 4K60HDMI/SDI H.265编码器采用最新高效H.265高清数字视频压缩…...

React state(及组件) 的保留与重置
当在树中相同的位置渲染相同的组件时,React 会一直保留着组件的 state return (<div><Counter />{showB && <Counter />} </div> ) // 当 showB 为 false, 第二个计数器停止渲染,它的 state 完全消失了。这是因为 React…...

flask返回的数据怎么是转义后的字符串啊
Flask在返回JSON数据时,默认情况下会对特殊字符进行转义,以确保数据能安全地在HTML页面中展示,避免XSS(跨站脚本攻击)等安全问题。如果不希望Flask对JSON响应中的字符串自动转义,通常是因为你希望在前端直接使用这些数据(例如作为JavaScript的一部分),那么需要确保数据…...

C++17并行算法与HIPSTDPAR
C17 parallel algorithms and HIPSTDPAR — ROCm Blogs (amd.com) C17标准在原有的C标准库中引入了并行算法的概念。像std::transform这样的并行版本算法保持了与常规串行版本相同的签名,只是增加了一个额外的参数来指定使用的执行策略。这种灵活性使得已经使用C标准…...

【什么是几度cms,主要功能有什么】
几度CMS内容管理框架是基于 PHP 语言采用最新 Thinkphp 作为开发框架生产的网站 内容管理框架,提供“电脑网站 手机网站 多终端 APP 接口”一体化网站技术解 决方案。她拥有强大稳定底层框架,以灵活扩展为主的开发理念,二次开发方便且…...
组合和外观模式
文章目录 组合模式1.引出组合模式1.院系展示需求2.组合模式基本介绍3.组合模式原理类图4.解决的问题 2.组合模式解决院系展示1.类图2.代码实现1.AbsOrganizationComponent.java 总体抽象类用于存储信息和定义方法2.University.java 第一层,University 可以管理 Coll…...

设置服务器禁止和ip通信
要禁止服务器与特定 IP 地址的通信,可以使用防火墙来设置规则。在 Ubuntu 上,iptables 是一个常用的防火墙工具。以下是使用 iptables 设置禁止与特定 IP 通信的步骤: 阻止所有进出的通信 如果你想阻止服务器与特定 IP 地址的所有通信&…...
)
中文技术文档的写作规范(搬运)
阮一峰老师的《中文技术文档的写作规范》搬运。 链接指路: https://github.com/ruanyf/document-style-guide/tree/master 内容:对中文技术文档从标题、文本、段落、数值、标点符号、文档体系、参考链接等七大方面进行了简明扼要的介绍。...
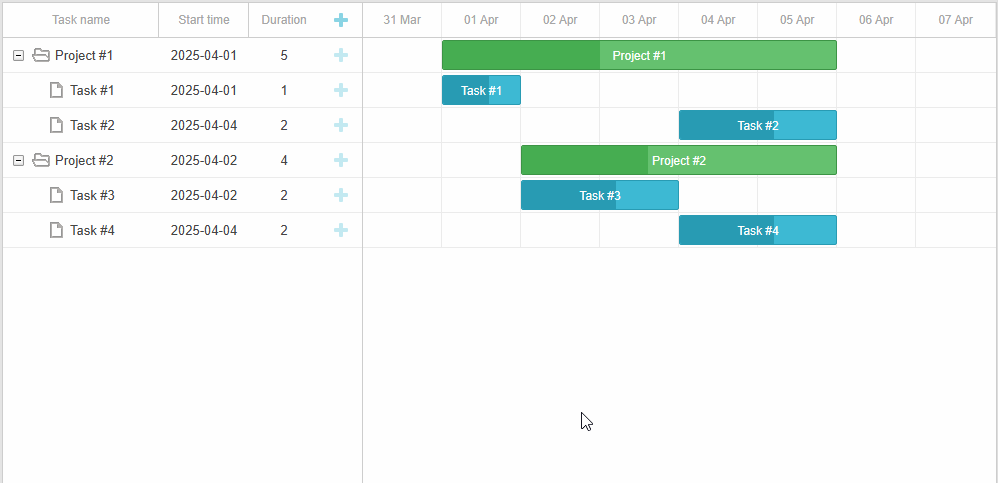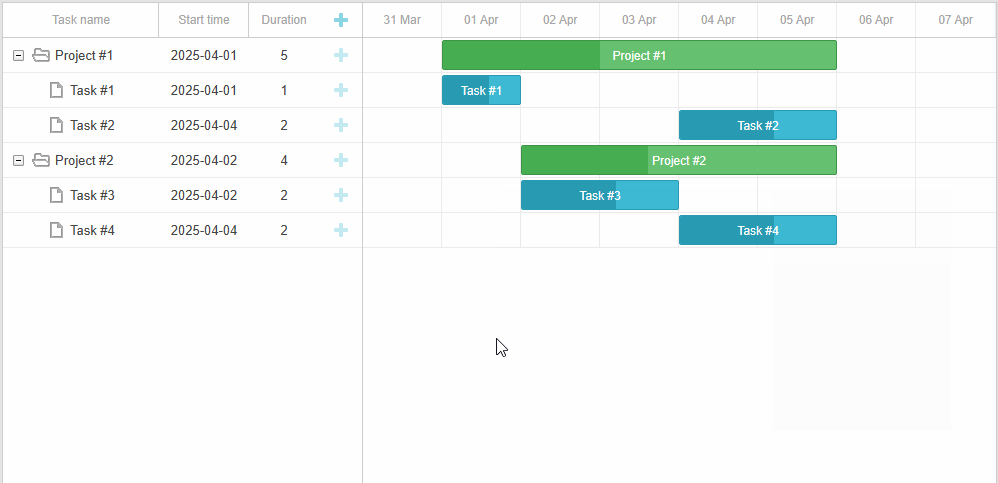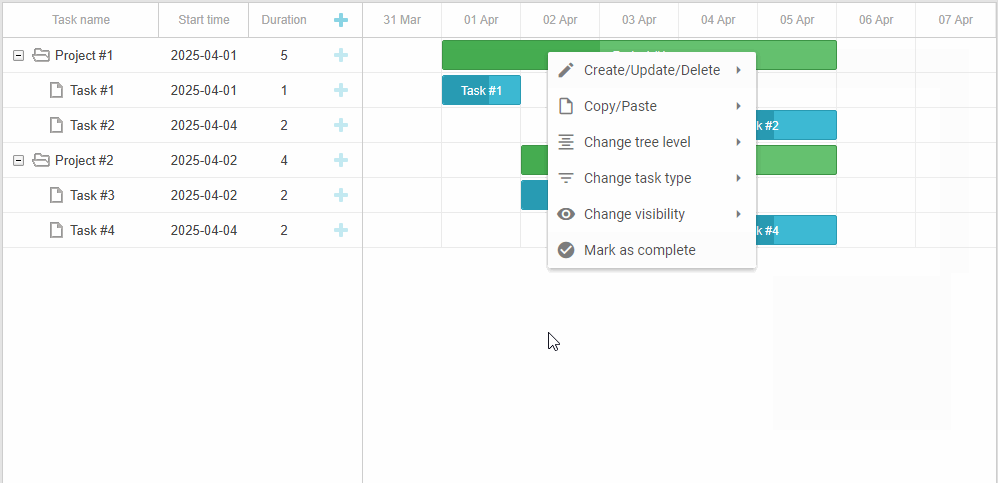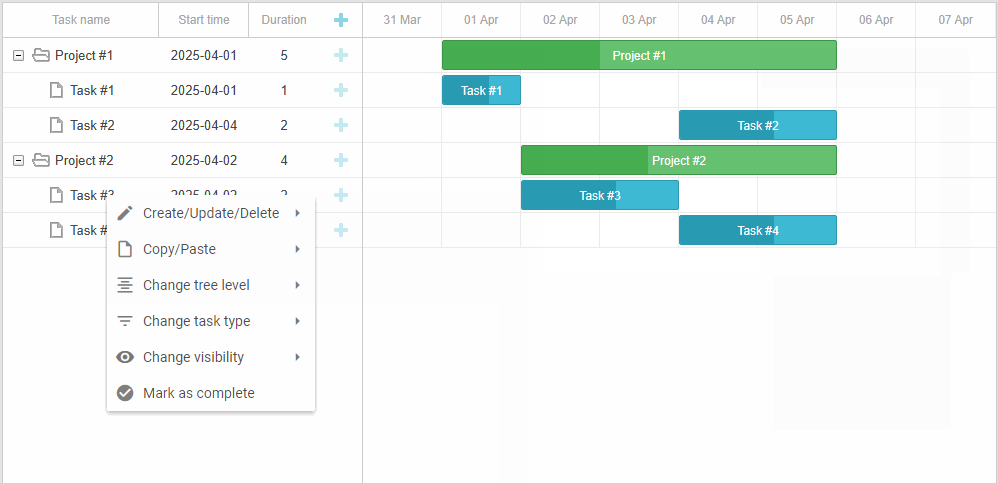
「实战应用」如何用DHTMLX将上下文菜单集成到JavaScript甘特图中(一)
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。 DHTMLX Gantt是一个高度可定制的工具,可以与项目管理应用程序所需的其他功能相补充。在本文中您将学习如何使用自定义上…...

Python使用策略模式生成TCP数据包
使用策略模式(Strategy Pattern)来灵活地生成不同类型的TCP数据包。 包括三次握手、数据传输和四次挥手。 from scapy.all import * from scapy.all import Ether, IP, TCP, UDP, wrpcap from abc import ABC, abstractmethodclass TcpPacketStrategy(A…...
无文件落地分离拆分-将shellcode从文本中提取-file
马子分为shellcode和执行代码. --将shellcode单独拿出,放在txt中---等待被读取执行 1-cs生成python的payload. 2-将shellcode进行base64编码 import base64code b en_code base64.b64encode(code) print(en_code) 3-将编码后的shellcode放入文件内 4-读取shellcod…...

MySQL 日志(一)
本篇主要介绍MySQL日志的相关内容。 目录 一、日志简介 常用日志 一般查询日志和慢查询日志的输出形式 日志表 二、一般查询日志 三、慢查询日志 四、错误日志 一、日志简介 常用日志 在MySQL中常用的日志主要有如下几种: 这些日志通常情况下都是关闭的&a…...

XML 编辑器:功能、选择与使用技巧
XML 编辑器:功能、选择与使用技巧 简介 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。由于其灵活性和广泛的应用,XML编辑器成为开发者、数据管理者和内容创作者的重要工具。本文将探讨XML编辑器的功能、选择标准以及…...
)
单例模式(设计模式)
文章目录 概述1. 饿汉式(hungry Initialization)2. 懒汉式(Lazy Initialization)3.双重检查锁定(Double-Checked Locking)4. 静态内部类(Static Inner Class)5. 枚举(Enu…...
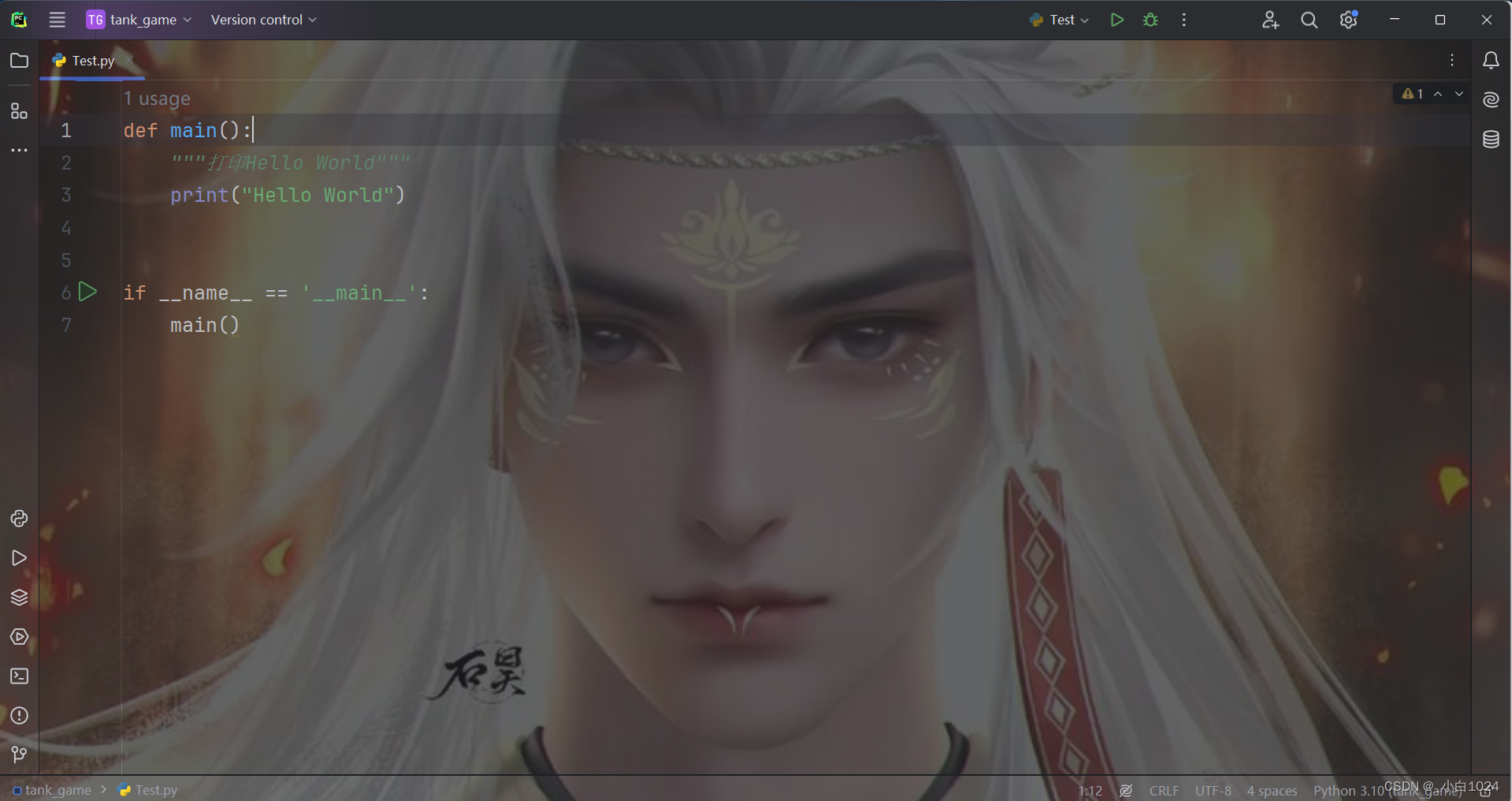
提升你的编程体验:自定义 PyCharm 背景图片
首先,打开 PyCharm 的设置菜单,点击菜单栏中的 File > Settings 来访问设置,也可以通过快捷键 CtrlAItS 打开设置。 然后点击Appearance & Behavior > Appearance。 找到Background image...左键双击进入。 Image:传入自己需要设置…...

SpringCloud与Dubbo区别?
相同点: dubbo与springcloud都可以实现RPC远程调用。 dubbo与springcloud都可以使用分布式、微服务场景下。 区别: dubbo有比较强的背景,在国内有一定影响力。 dubbo使用zk或redis作为作为注册中心 springcloud使用eureka作为注册中心 dubbo支持多种协议,默认使用…...
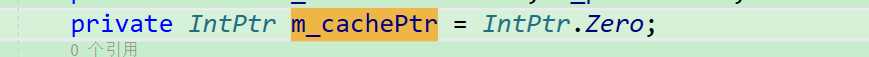
简单Mesh多线程合并,使用什么库性能更高
1)简单Mesh多线程合并,使用什么库性能更高 2)Unity Semaphore.WaitForSignal耗时高 3)VS编辑的C#代码注释的中文部分乱码 4)变量IntPtr m_cachePtr切换线程后变空 这是第389篇UWA技术知识分享的推送,精选了…...

长亭培训加复习安全产品类别
下面这个很重要参加hw时要问你用的安全产品就有这个 检测类型产品 偏审计 安全防御类型 EDR类似于杀毒软件 安全评估 任何东西都要经过这个机械勘察才能上线 安全管理平台 比较杂 比较集成 审计 漏扫 评估 合在这一个平台 也有可能只是管理 主机理解为一个电脑 安了终端插件…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
