当前位置： 首页 > news >正文

使用fvm切换flutter版本

news 2026/3/31 16:57:54

切换flutter版本
下载fvm
1、dart pub global activate fvm   dart下载fvm
2、warning中获取下载本地的地址
3、添加用户变量path： 下载地址 终端查看fvm版本  fvm --version
4、指定fvm文件缓存地址 fvm config --cache-path C:\src\fvm（自定义地址）
5、设置用户变量FVM_HOME: C:\src\fvm 注意之前有设置过flutter环境变量这时可以先删除掉试试可能会影响之后切换flutter版本
6、安装fluttersdk   flutter install 指定版本号

7、查看flutter版本列表fvm list 

8、全局切换flutter版本fvm global

 

config   设置FVM的配置
dart   代理dart命令
destroy   通过删除FVM目录销毁FVM缓存
doctor   显示有关环境和项目配置的信息。
exec  使用配置的Flutter SDK执行脚本
flavor 在不同的项目风格之间切换
flutter   代理flutter命令
global    将Flutter SDK版本设置为全局
install    安装Flutter SDK版本
list   列出已安装的Flutter SDK版本
releases    查看所有可供安装的Flutter SDK版本。
remove   删除Flutter SDK版本
spawn   在Flutter版本上生成命令
use      要在项目中使用的Sets Flutter SDK版本

相关文章：

使用fvm切换flutter版本

切换flutter版本 下载fvm 1、dart pub global activate fvm dart下载fvm 2、warning中获取下载本地的地址 3、添加用户变量path： 下载地址 终端查看fvm版本 fvm --version 4、指定fvm文件缓存地址 fvm config --cache-path C:\src\fvm（自定义地址&…...

编程日记 2024/6/15 12:32:01

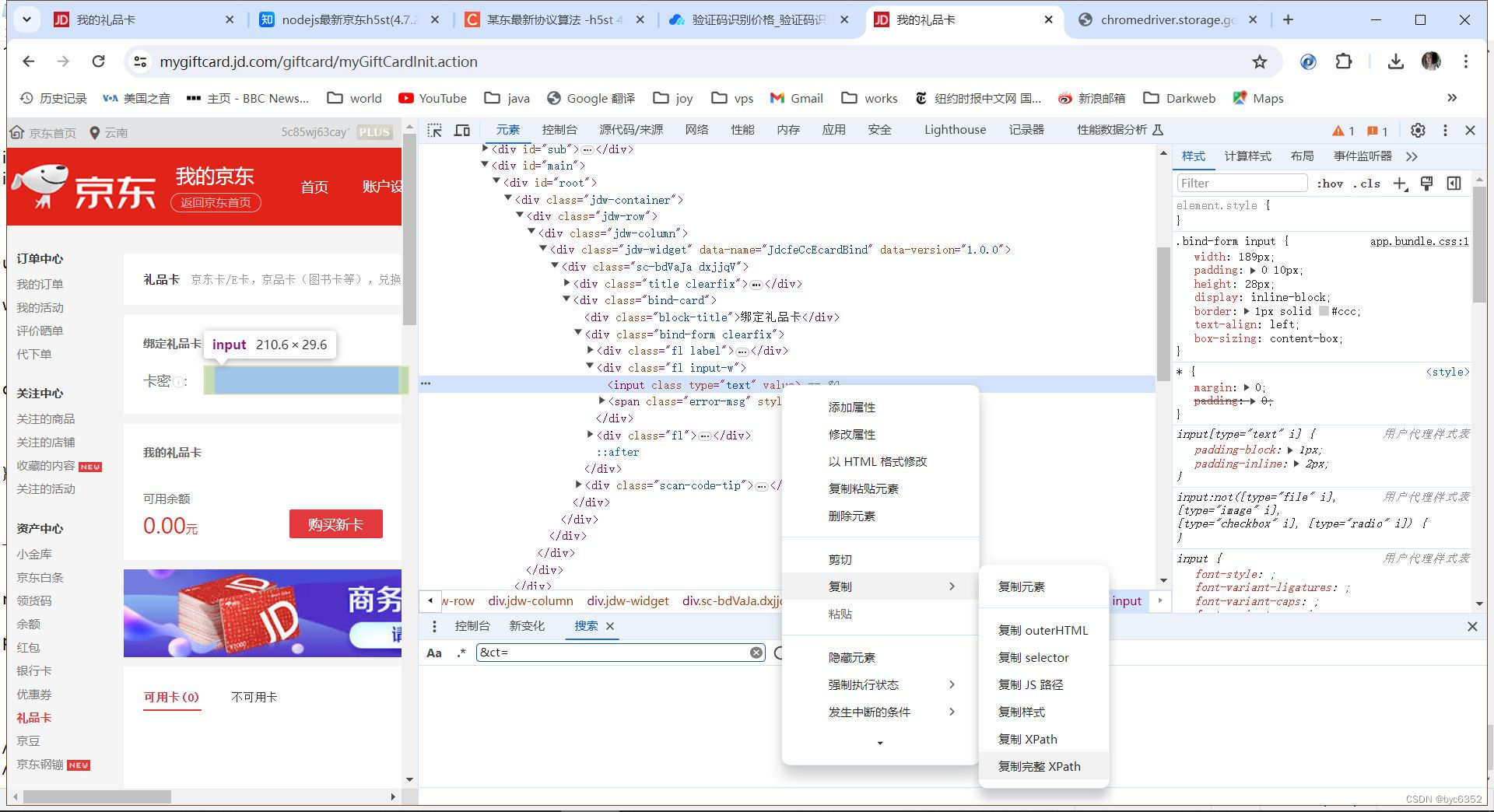
python通过selenium实现自动登录及轻松过滑块验证、点选验证码（2024-06-14）

一、chromedriver配置环境搭建 请确保下载的驱动程序与你的Chrome浏览器版本匹配，以确保正常运行。 1、Chrome版本号 chrome的地址栏输入chrome://version，自然就得到125.0.6422.142 版本 125.0.6422.142（正式版本） （…...

编程日记 2024/6/15 12:31:00

【C++】开源项目收集

C 是一种强大的、静态类型的通用编程语言，它的开源生态系统非常丰富，拥有众多高质量的项目。以下是一些知名的C开源项目： Boost: 这是一个庞大的库集合，提供了大量的实用工具和组件，如文件系统、网络编程、智能指针等&…...

编程日记 2024/6/15 12:29:59

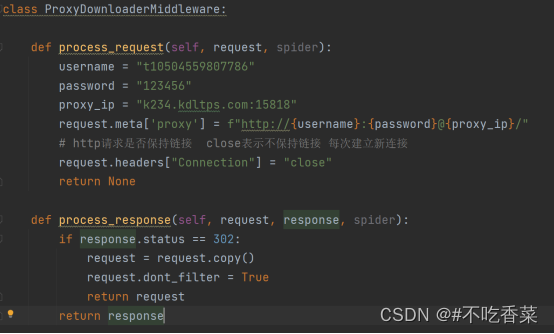
爬虫相关面试题

一，如何抓取一个网站？ 1，去百度和谷歌搜一下这个网站有没有分享要爬取数据的API 2, 看看电脑网页有没有所需要的数据，写代码测试调查好不好拿，如果好拿直接开始爬取 3，看看有没有电脑能打开的手机网页&a…...

编程日记 2024/6/15 12:28:58

Spring Cloud Netflix 之 Ribbon

前言 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家：https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言前言1、负载均衡1.1、服务端负载均衡1.2、客户端负载均衡 2、Ribbon实现服务…...

编程日记 2024/6/15 12:27:57

C语言怎样记住那么多的颜⾊？

一、问题 ⾚、橙、⻩、绿、⻘、蓝、紫，如此之多的颜⾊，数字不好记，英⽂看程序还可以， 直接写也不好写。那么怎样记住那么多的颜⾊呢？ 二、解答 颜⾊枚举值如下： enum COLORS {BLACK, /*O⿊*/BLUE, …...

编程日记 2024/6/15 12:26:56

LabVIEW软件开发任务的工作量估算方法

在开发LabVIEW软件时，如何准确估算软件开发任务的工作量。通过需求分析、功能分解、复杂度评估和资源配置等步骤，结合常见的估算方法，如专家判断法、类比估算法和参数估算法，确保项目按时按质完成，提供项目管理和资源分…...

编程日记 2024/6/15 12:25:55

【已解决】引入 element 组件无法使用编译错误 ERROR Failed to compile with 1 error

如果大家使用这个vue 配合 element 框架不熟练，当你顺利按照文档安装好 vue 和 element 的时候想要使用element 的组件时候确无法展示出来，甚至报错。不妨看看是不是这个问题， 1.首先使用element 的时候，前提是把必须要的 elemen…...

编程日记 2024/6/15 12:23:53

Prometheus的四种指标类型

目录 一、Counter 计数器 1.1Counter 是计数器类型 1.2Counter 类型示例 二、Gauge 仪表盘 2.1Gauge是测量器类型 2.2Gauge 类型示例 三、Histogram 累积直方图 3.1Histogram 作用及特点 3.2使用 histogram 柱状图 四、Summary 摘要 一、Counter 计数器 1.1Counter …...

编程日记 2024/6/15 12:20:49

FastDFS SpringBoot 客户端 Demo搭建，支持文件上传下载

一、准备 fastdfs-client-java 依赖包 1、从 Git 下载 FastDFS java client SDK 源码 https://github.com/happyfish100/fastdfs-client-java.git<fastdfs-client-java 源码见附件> 2、使用ant从源码构建 ant clean package3、使用maven从源码安装 mvn clean instal…...

编程日记 2024/6/15 12:18:46

十大成长型思维：定位思维、商业思维、时间管理思维、学习成长思维、精力管理思维、逻辑表达思维、聚焦思维、金字塔原理、目标思维、反思思维

一、定位思维 定位思维是一种在商业和管理领域中至关重要的思维模式&#xff0c;它涉及到如何在顾客心智中确立品牌的独特位置&#xff0c;并使其与竞争对手区分开来。以下是关于定位思维的清晰介绍&#xff1a; 1、定义 定位思维是一种从潜在顾客的心理认知出发&#xff0c;通…...

编程日记 2024/6/15 12:14:43

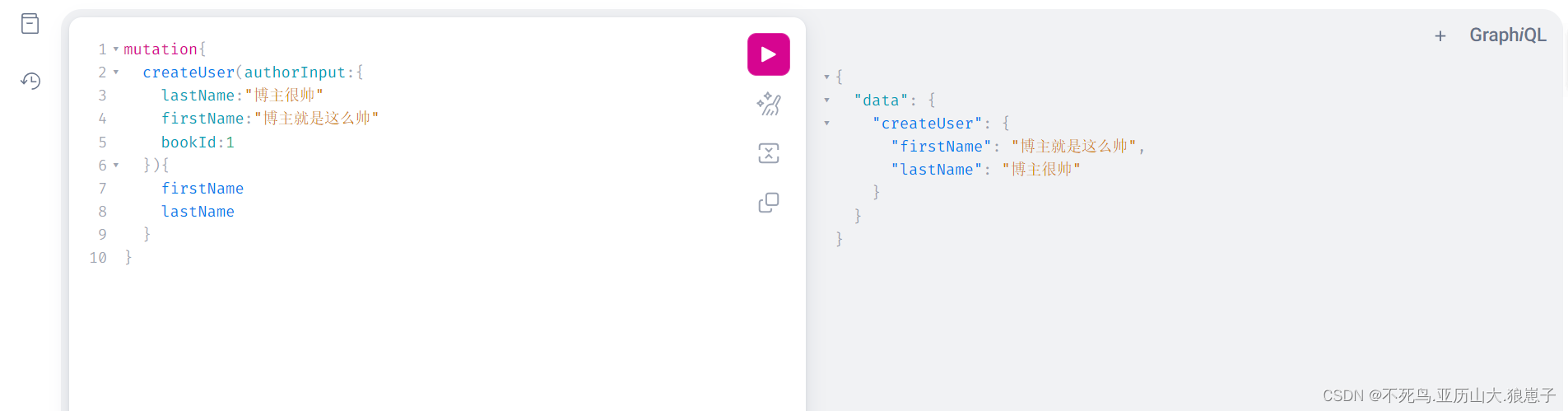
GraphQL（9）：Spring Boot集成Graphql简单实例

1 安装插件 我这边使用的是IDEA&#xff0c;需要先按照Graphql插件&#xff0c;步骤如下&#xff1a; &#xff08;1&#xff09;打开插件管理 在IDEA中&#xff0c;打开主菜单&#xff0c;选择 "File" -> "Settings" (或者使用快捷键 Ctrl Alt S …...

编程日记 2024/6/15 12:13:42

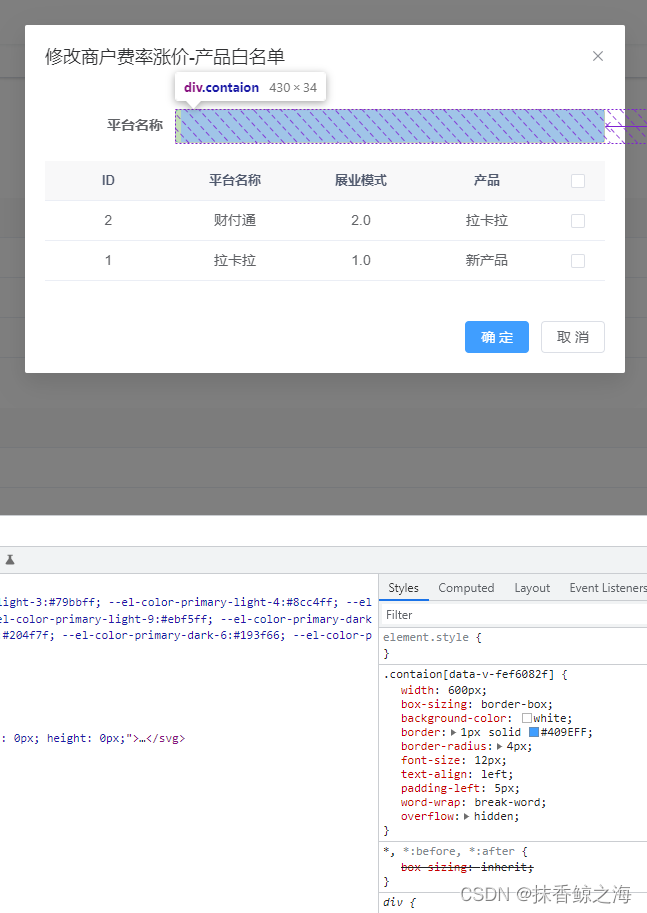
vue3+ Element-Plus 点击勾选框往input中动态添加多个tag

实现效果&#xff1a; template&#xff1a; <!--产品白名单--><div class"con-item" v-if"current 0"><el-form-item label"平台名称"><div class"contaion" click"onclick"><!-- 生成的标签 …...

编程日记 2024/6/15 12:12:40

唯美仙侠手游【九幽仙域】win服务端+GM后台+详细教程

资源下载地址&#xff1a;九幽仙域搭建-...

编程日记 2024/6/15 12:11:39

Qt creator day2练习

使用手动连接&#xff0c;将登录框中的取消按钮使用第二种方式&#xff0c;右击转到槽&#xff0c;在该函数中&#xff0c;调用关闭函数&#xff0c;将登录按钮使用Qt4版本的连接到自定义的槽函数中&#xff0c;在槽函数中判断ui界面上输入的账号是否为“admin”&#xff0c;密…...

编程日记 2024/6/15 12:10:37

哪里有海量的短视频素材，以及短视频制作教程？

在当下&#xff0c;短视频已成为最火爆的内容形式之一&#xff0c;尤其是在抖音上。但很多创作者都面临一个问题&#xff1a;视频素材从哪里来&#xff1f;怎么拍摄才能吸引更多观众&#xff1f;别担心&#xff0c;今天我将为大家推荐几个宝藏网站&#xff0c;确保你素材多到用…...

编程日记 2024/6/15 12:09:36

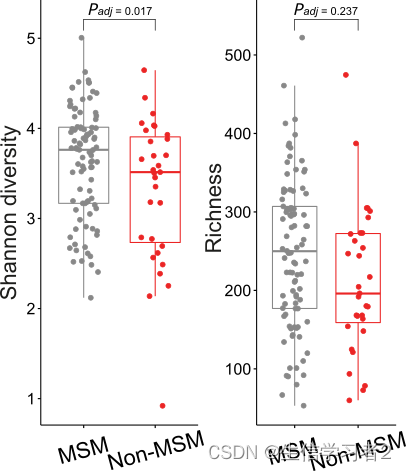
文章MSM_metagenomics（三）：Alpha多样性分析

欢迎大家关注全网生信学习者系列&#xff1a; WX公zhong号&#xff1a;生信学习者Xiao hong书&#xff1a;生信学习者知hu&#xff1a;生信学习者CDSN&#xff1a;生信学习者2 介绍 本教程使用基于R的函数来估计微生物群落的香农指数和丰富度&#xff0c;使用MetaPhlAn prof…...

编程日记 2024/6/15 12:08:35

Web前端与其他前端：深度对比与差异性剖析

Web前端与其他前端&#xff1a;深度对比与差异性剖析 在快速发展的前端技术领域&#xff0c;Web前端无疑是其中最耀眼的明星。然而&#xff0c;当我们谈论前端时&#xff0c;是否仅仅指的是Web前端&#xff1f;实际上&#xff0c;前端技术还包括了许多其他细分领域。本文将从四…...

编程日记 2024/6/15 12:06:33

AI 客服定制：LangChain集成订单能力

为了提高AI客服的问题解决能力&#xff0c;我们引入了LangChain自定义能力&#xff0c;并集成了订单能力。这使得AI客服可以根据用户提出的问题&#xff0c;自动调用订单接口&#xff0c;获取订单信息&#xff0c;并结合文本知识库内容进行回答。这种能力的应用&#xff0c;使得…...

编程日记 2024/6/15 12:05:32

【计算机毕业设计】242基于微信小程序的外卖点餐系统

&#x1f64a;作者简介&#xff1a;拥有多年开发工作经验&#xff0c;分享技术代码帮助学生学习&#xff0c;独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。&#x1f339;赠送计算机毕业设计600个选题excel文件&#xff0c;帮助大学选题。赠送开题报告模板&#xff…...

编程日记 2024/6/15 12:04:31

Zotero中文文献管理终极指南：茉莉花插件一键解决三大痛点

Zotero中文文献管理终极指南&#xff1a;茉莉花插件一键解决三大痛点 【免费下载链接】jasminum A Zotero add-on to retrive CNKI meta data. 一个简单的Zotero 插件&#xff0c;用于识别中文元数据 项目地址: https://gitcode.com/gh_mirrors/ja/jasminum 如果你正在使…...

编程新知 2026/3/31 16:46:23

实战应用：使用快马平台为vmware17部署生成企业级健康检查与配置方案

在实际的企业IT环境中&#xff0c;部署VMware vSphere 17&#xff08;以下简称VMware 17&#xff09;这类虚拟化平台往往不是简单的安装过程&#xff0c;而是需要综合考虑硬件兼容性、系统配置、安全策略等多方面因素。为了确保部署过程的顺利和后续运行的稳定&#xff0c;我们…...

编程新知 2026/3/31 16:42:22

三三复制商业模式系统介绍

三三复制商业模式系统介绍&#xff1a;裂变逻辑与合规落地全解析在数字经济时代&#xff0c;社交电商与分销模式的创新成为企业突破增长瓶颈的关键。三三复制模式以其几何级数的裂变效率、清晰的层级收益结构和低门槛参与机制&#xff0c;在电商、直销等领域展现出强大的生命力…...

编程新知 2026/3/31 16:05:45

Windows自定义部署神器：从零开始的安装介质制作指南

Windows自定义部署神器&#xff1a;从零开始的安装介质制作指南 【免费下载链接】MediaCreationTool.bat Universal MCT wrapper script for all Windows 10/11 versions from 1507 to 21H2! 项目地址: https://gitcode.com/gh_mirrors/me/MediaCreationTool.bat 你是否…...

编程新知 2026/3/31 15:47:30

ICLR 2025论文解读│PointOBB-v2：单点监督下的高效有向目标检测新突破

1. PointOBB-v2&#xff1a;单点监督的革命性突破 有向目标检测一直是计算机视觉领域的重要研究方向&#xff0c;特别是在遥感图像分析、自动驾驶和工业检测等实际应用中。传统的有向边界框&#xff08;OBB&#xff09;标注需要人工精确标注目标的旋转角度和四个顶点坐标&…...

编程新知 2026/3/31 15:39:27

ComfyUI-FramePackWrapper终极指南：3种AI视频生成模型加载方案深度对比

ComfyUI-FramePackWrapper终极指南&#xff1a;3种AI视频生成模型加载方案深度对比 【免费下载链接】ComfyUI-FramePackWrapper 项目地址: https://gitcode.com/gh_mirrors/co/ComfyUI-FramePackWrapper 在AI视频生成领域&#xff0c;ComfyUI-FramePackWrapper是一款革…...

编程新知 2026/3/31 13:53:11

别再到处找了！这12个三维点云开源数据集，够你从入门到项目实战

三维点云实战指南&#xff1a;12个精选开源数据集与精准匹配策略 当你第一次打开三维点云处理软件&#xff0c;面对空白的项目界面&#xff0c;最迫切的问题往往是&#xff1a;"我该从哪里获取高质量的训练数据&#xff1f;"这个问题困扰过每一位初学者&#xff0c;…...

编程新知 2026/3/31 13:02:37

选择性记忆提取，把人类遗忘机制用在了RAG上，这架构真有点东西

当前大模型处理长文本面临三大瓶颈&#xff1a;算力爆炸&#xff1a;传统注意力机制随文本长度呈二次方增长&#xff08;O(N)&#xff09;&#xff0c;百万级token直接OOMRAG碎片化&#xff1a;检索增强生成将文档切成独立片段&#xff0c;破坏多跳推理的逻辑链条记忆遗忘&…...

编程新知 2026/3/31 13:00:37

P3C黄山版突破式迁移指南：无缝升级Java代码规范检查体系

P3C黄山版突破式迁移指南&#xff1a;无缝升级Java代码规范检查体系 【免费下载链接】p3c Alibaba Java Coding Guidelines pmd implements and IDE plugin 项目地址: https://gitcode.com/gh_mirrors/p3/p3c 在Java开发团队中&#xff0c;代码规范检查工具的升级往往伴…...

编程新知 2026/3/31 12:19:42

5个场景带你体验KISS Translator：让网页双语阅读不再是难题

5个场景带你体验KISS Translator&#xff1a;让网页双语阅读不再是难题 【免费下载链接】kiss-translator A simple, open source bilingual translation extension & Greasemonkey script (一个简约、开源的 双语对照翻译扩展 & 油猴脚本) 项目地址: https://gitcod…...

编程新知 2026/3/31 12:01:35