算法01 递推算法及相关问题详解【C++实现】
目录
递推的概念
训练:斐波那契数列
解析
参考代码
训练:上台阶
参考代码
训练:信封
解析
参考代码
递推的概念
递推是一种处理问题的重要方法。
递推通过对问题的分析,找到问题相邻项之间的关系(递推式),从起点出发(首项或者末项)然后使用循环不断地迭代,得到最后需要的结果。
训练:斐波那契数列
对于Fibonacci数列,已知:fib(1) = 1; fib(2) = 1; 从第三项开始满足公式fib(i) = fib(i-1) + fib(i-2)。输入一个整数n(1<=n<=100),求fib(n)的值。
【输入描述】一行:一个整数n。
【输出描述】一行:feibonacci数列第n项的值
【样例输入】5
【样例输出】5
解析
1.问题求的是斐波那契数列第i项的数值。
2.前两项的数值,题目中已经给出,分别为:
fib(1) = 1; fib(2) = 1;
3.从第3项开始,满足如下规律:
fib(i) = fib(i-1) + fib(i-2);
即当前项由前两项之和构成。
4.我们可以根据题目给出的fib(1)、fib(2)推出fib(3),
再按照顺序由fib(2)、fib(3)推出fib(4),以此类推。
参考代码
#include<bits/stdc++.h>
using namespace std;
int main()
{long long n,f1,f2,f3;cin>>n;f1=f2=f3=1;//初始化,f3表示第n项for(long long i=3;i<=n;i++){f3=f1+f2;f1=f2;f2=f3;}cout<<f3;return 0;
}训练:上台阶
楼梯有n(1<=n<=100)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一步上3阶,编程计算共有多少种不同的走法。
【输入描述】输入的每一行包括一组测试数据,即为台阶数n。最后一行为0,表示测试结束。
【输出描述】每一行输出对应一行输入的结果,即为走法的数目。
【样例输入】
1
2
3
4
0
【样例输出】
1
2
4
7
参考代码
#include<bits/stdc++.h>
using namespace std;
long long a[105];
//a[i]表示i层楼梯方案数
int main()
{int n,t;a[1]=1,a[2]=2,a[3]=4;//边界条件while(1){cin>>t;if(!t) break;if(a[t]){ //如果已经计算过,直接输出cout<<a[t]<<endl;continue;}for(int i=4;i<=t;i++)a[i]=a[i-1]+a[i-2]+a[i-3];//从第4层楼梯开始//每一步有3种方案:1阶、2阶、3阶//分别对应 a[i-1]、a[i-2]、a[i-3]cout<<a[t]<<endl;}return 0;
}
训练:信封
现在有n封信和n个信封,如果所有的信都装错了信封。求所有信都装错信封共有多少种不同情况。
【输入描述】1行:输入一个整数n。
【输出描述】1行:输出一个整数,表示所有的情况数。
【样例输入】4
【样例输出】9
解析
先任取一封信,此时可供选择的信封有:n-1种情况。
每种情况下,我们在放置这封信的时候有2种方案:
- 这封信的位置,不与剩余的任意一封信互换,此时,剩余的问题就是:将n-1封信,错放在n-1个信封里,即f(n-1)
- 这封信的位置,与剩余的任意一封信互换,此时会有2个信封被使用掉。剩余的问题就是:将n-2封信,错放在n-2个信封里,即f(n-2),得出递推式:f(n)=(n-1)*(f(n-1)+f(n-2))。边界是:f(1)=0,f(2)=1。
参考代码
#include<bits/stdc++.h>
using namespace std;
long long f[25];
int main()
{int n;cin>>n;f[1]=0,f[2]=1;for(int i=3;i<=n;i++){f[i]=(i-1)*(f[i-1]+f[i-2]);}cout<<f[n];return 0;
} 从入门到算法,再到数据结构,查看全部文章请点击此处![]() http://www.bigbigli.com/
http://www.bigbigli.com/
相关文章:
算法01 递推算法及相关问题详解【C++实现】
目录 递推的概念 训练:斐波那契数列 解析 参考代码 训练:上台阶 参考代码 训练:信封 解析 参考代码 递推的概念 递推是一种处理问题的重要方法。 递推通过对问题的分析,找到问题相邻项之间的关系(递推式&a…...
自动化测试火狐下载文件
本篇文章介绍selenium中火狐浏览器如何下载文件。比如我想把这个MP4的视频文件下载下来。 点击之后查看下载的类型是video/mp4 指定使用火狐浏览器 profile webdriver.FirefoxOptions() # 设置firefox默认的下载路径,0表示桌面,1表示我的下载…...
基于JSP技术的定西扶贫惠农推介系统
开头语:你好呀,我是计算机学长猫哥!如果有相关需求,文末可以找到我的联系方式。 开发语言:JSP 数据库:MySQL 技术:B/S架构、JSP技术 工具:Eclipse、MySQL、Tomcat 系统展示 首…...

Linux 终端窗口设置为透明
Linux 终端窗口设置为透明 打开终端 右键鼠标 选择Profile Preferences 点击Background 选择 Transparent background 拖动滑条调整透明度 完成。...

MySQL 中 Varchar(50) 和 varchar(500) 区别是什么?
一. 问题描述 我们在设计表结构的时候,设计规范里面有一条如下规则: 对于可变长度的字段,在满足条件的前提下,尽可能使用较短的变长字段长度。 为什么这么规定?我在网上查了一下,主要基于两个方面 基于存储空间的考…...

强化RAG:微调Embedding还是LLM?
为什么我们需要微调? 微调有利于提高模型的效率和有效性。它可以减少训练时间和成本,因为它不需要从头开始。此外,微调可以通过利用预训练模型的功能和知识来提高性能和准确性。它还提供对原本无法访问的任务和领域的访问,因为它…...

提取 Excel单元格文本下的超链接
在Excel中,可以使用内置的函数来提取单元格中的超链接地址。如果你有一个包含超链接的单元格,例如B1,你可以使用以下步骤来提取这个超链接: 在一个新的单元格(例如C1)中,输入以下公式ÿ…...

一键安全体检!亚信安全携手鼎捷软件推出企业安全体检活动 正式上线
亚信安全联合鼎捷软件股份有限公司(以下简称“鼎捷软件”)正式推出“一键安全体检”服务。亚信安全网络安全专家将携手鼎捷软件数据安全专家,围绕企业的数智安全状况,进行问题探索与治愈、新问题预测与预警,在全面筛查…...
)
numpy - array(1)
一维数据:向量 二位数据:矩阵 维度超过三维的数据:张量 这些数据在numpy中统称array (1)使用穷举法创建多为数据,接受列表或者元组类型的数据 a numpy.array([1, 2, 3]) b numpy.array([[1, 2, 3], (4, 5, 6), [7, 8, 9]]) (2)创建所有元…...
师彼长技以助己(6)递归思维
师彼长技以助己(6)递归思维 递归思维-小游戏 思维小游戏 思维 小游戏:1 玩一个从1或2开始往上加的游戏,谁加到20就赢 如何保证一定赢呢?我们倒推,要先到20的话,谁先到17就赢,如此…...

Kali Linux 2024.2
Kali Linux 2024.2 版本(t64、GNOME 46 和社区包) 比平常晚了一点,但 Kali 2024.2 来了!延迟是由于实现这一目标的幕后变化所致,这也是人们关注的焦点。社区提供了大量帮助,这次他们不仅添加了新的软件包&…...
【Spine学习08】之短飘,人物头发动效制作思路
上一节说完了跑步的, 这节说头发发型。 基础过程总结: 1.创建骨骼(头发需要在上方加一个总骨骼) 2.创建网格(并绑定黄线) 3.绑定权重(发根位置的顶点赋予更多总骨骼的权重) 4.切换到…...

chatgpt的命令词
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

用python把docx批量转为pdf
为保证转换质量,本文的方法是通过脚本和com技术调用office自带的程序进行转换的,因此需要电脑已经装有office。如果希望不装office也能用,则需要研究OpenXML技术,后面实在闲的慌(退休)再搞。 安装所需库 …...

项目采购管理
目录 1.概述 2.三个子过程 2.1.规划采购管理 2.2.实施采购 2.3.控制采购 2.4.归属过程组 3.应用场景 3.1.十个应用场景 3.2.软件开发项目 3.2.1. 需求识别和分析 3.2.2. 制定采购计划 3.2.3. 发布采购请求 3.2.4. 供应商评估与选择 3.2.5. 合同签订 3.2.6. 采购…...

Elasticsearch 认证模拟题 - 18
一、题目 为一个索引,按要求设置以下 dynamic Mapping 一切 text 类型的字段,类型全部映射成 keyword一切以 int_ 开头命名的字段,类型都设置成 integer 1.1 考点 字段的动态映射 1.2 答案 # 创建索引和索引模板 PUT my_index {"m…...

Python基础-速记笔记
Python的基础数据类型都有哪些? 1、字符串(string)2、布尔类型(bool)3、整数(int) 4、浮点数(float)5、列表(list)6、集合(set)7、元组(tuple)8、字典(dict) 其中不可变类型有: 字符串(string)、布尔类型(bool)、整数(int) 、浮点数(float)、元组(tup…...

青少年编程与数学 01-001开始使用计算机 02课题、计算机操作系统3_3
青少年编程与数学 01-001开始使用计算机 02课题、计算机操作系统3_3 四、Linux操作系统安装(一) 准备工作(二)设置BIOS/UEFI(三) 安装Linux(四)磁盘分区(五)安…...
填表统计预约打卡表单系统(FastAdmin+ThinkPHP+UniApp)
填表统计预约打卡表单系统:一键搞定你的预约与打卡需求 填表统计预约打卡表单系统是一款基于FastAdminThinkPHPUniApp开发的一款集信息填表、预约报名,签到打卡、活动通知、报名投票、班级统计等功能的自定义表单统计小程序。 📝 一、引言…...
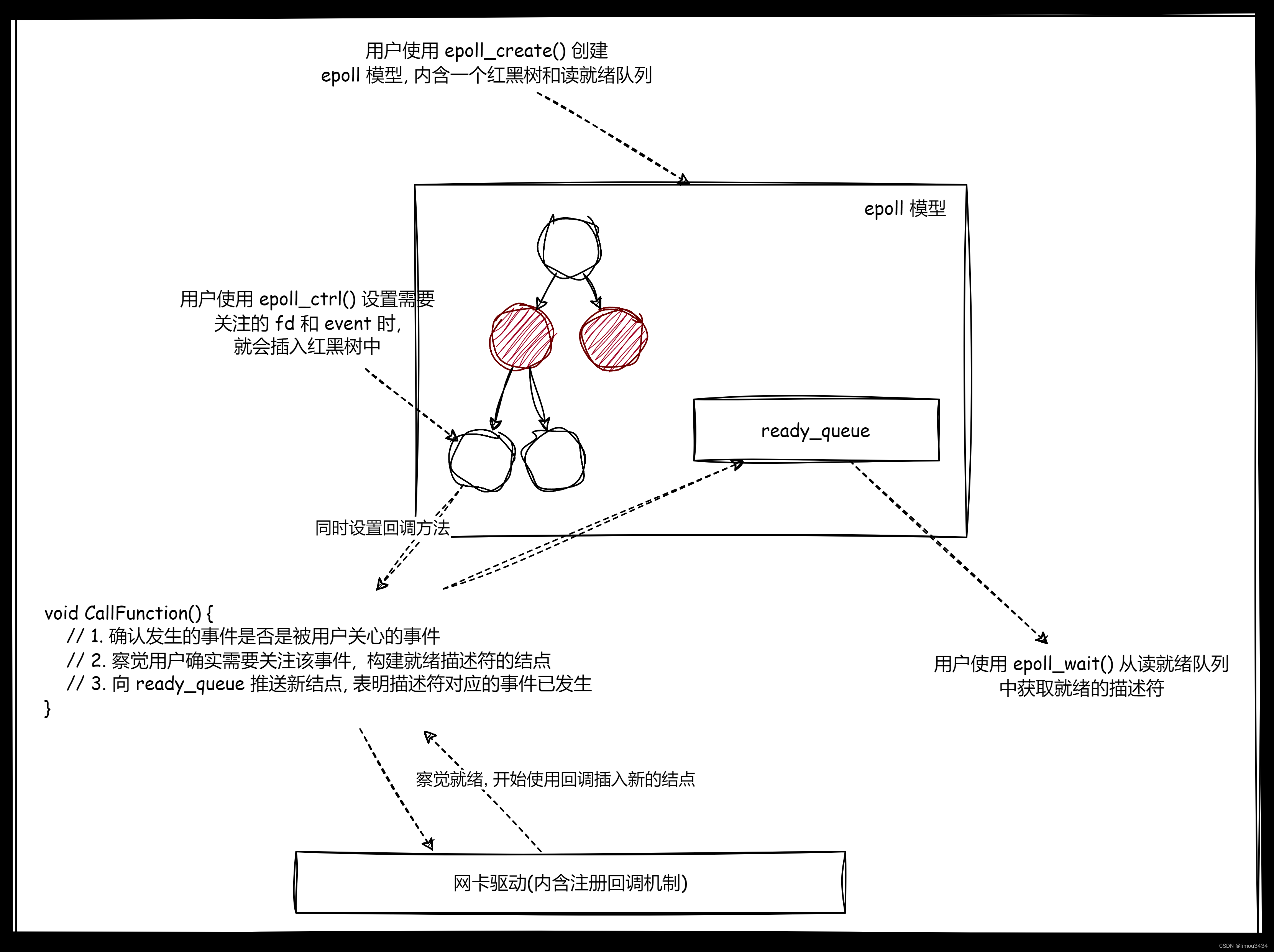
IO模型和多路转接
叠甲:以下文章主要是依靠我的实际编码学习中总结出来的经验之谈,求逻辑自洽,不能百分百保证正确,有错误、未定义、不合适的内容请尽情指出! 文章目录 1.IO 概要1.1.IO 低效原因1.2.IO 常见模型1.2.1.阻塞 IO1.2.2.非阻…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
