merkle tree中文
Merkle tree
- merkle tree中文文档
- 英文文档
#include <cstdlib>
#include <string>
#include <bitcoin/bitcoin.hpp>BC_USE_LIBBITCOIN_MAINusing namespace bc;bc::hash_digest calculate_merkle_root(bc::hash_list &merkle);int bc::main(int argc, char *argv[])
{bc::cout << "测试 merkle_tree" << std::endl;bc::hash_list tx_hashes{bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000000"),bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000011"),bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000022"),};bc::hash_digest merkle_root = calculate_merkle_root(tx_hashes);bc::string right_hash = "d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3";assert(right_hash == bc::encode_hash(merkle_root));bc::cout << bc::encode_hash(merkle_root) << std::endl;return 0;
}/*** 计算 merkle root*/
bc::hash_digest calculate_merkle_root(bc::hash_list &merkle)
{if (merkle.empty()){return bc::null_hash;}if (merkle.size() == 1){return merkle[0];}// 如果不是偶数, 则将最后一个元素复制一份凑成偶数if (0 != (merkle.size() & 1)){merkle.push_back(merkle.back());}assert(0 == (merkle.size() & 1));bc::hash_list tmp_merkle;for (auto it = merkle.begin(); it != merkle.end(); it += 2){bc::data_chunk concat_data(bc::hash_size * 2);auto concat = bc::make_unsafe_serializer(concat_data.begin());concat.write_hash(*it);concat.write_hash(*(it + 1));//assert(concat. == concat_data.end());bc::hash_digest new_root = bc::bitcoin_hash(concat_data);tmp_merkle.push_back(new_root);}merkle = tmp_merkle; //size 变为原来的一半return calculate_merkle_root(merkle); //继续递归, 当然可以用迭代代替
}相关文章:

merkle tree中文
Merkle tree merkle tree中文文档英文文档 #include <cstdlib> #include <string> #include <bitcoin/bitcoin.hpp>BC_USE_LIBBITCOIN_MAINusing namespace bc;bc::hash_digest calculate_merkle_root(bc::hash_list &merkle);int bc::main(int argc, …...

制作自己的 @OnClick、@OnLongClick(告别 setOnClickListener,使用注解、反射和动态代理)
前言 前面我们说过 ButterKnife 这个库,这个库实现不仅实现了 View 的绑定,而且还提供了大量的注解如 BindView、OnClick、OnLongClick 等来简化开发过程中事件绑定。而这些功能的实现是通过 APT 也就是注解处理器,在编译期间生成 Java 代码…...

Android基础-RecyclerView的优点
一、引言 在Android开发中,RecyclerView是一个强大而灵活的控件,用于展示大量数据集合的视图。相比于传统的ListView和GridView,RecyclerView提供了更高的性能、更多的布局选择和更丰富的交互体验。本文将详细阐述RecyclerView的功能作用以及…...
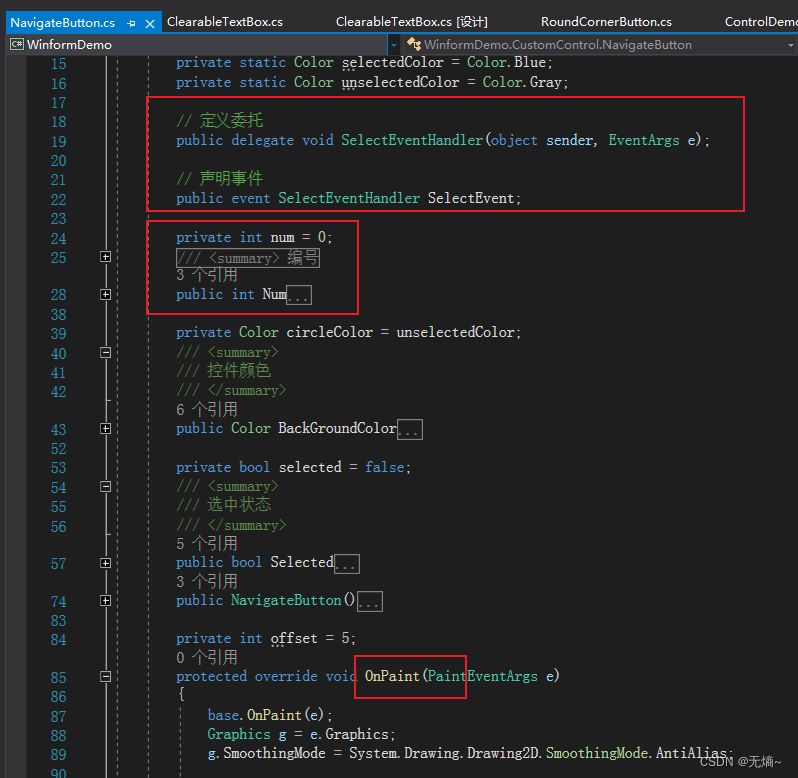
C# Winform 用户控件,扩展控件,自定义控件综合实例
Control类是Windows窗体控件的基类,它提供了在 Windows 窗体应用程序中进行可视显示所需的基础结构,可以通过继承来扩展熟悉的用户控件和现有控件的功能。本列介绍三种不同自定义控件以及怎么创建他们。 自定义控件分类 用户控件:基本控件的…...

经济学和金融学有什么区别?
中文版 金融学和经济学是两个密切相关但有所不同的学科,它们各自侧重于不同的研究领域和方法。 经济学 (Economics) 经济学是研究如何配置有限资源以满足人类无限需求的学科。它可以分为两个主要分支: 宏观经济学 (Macroeconomics): 研究经济整体的行…...
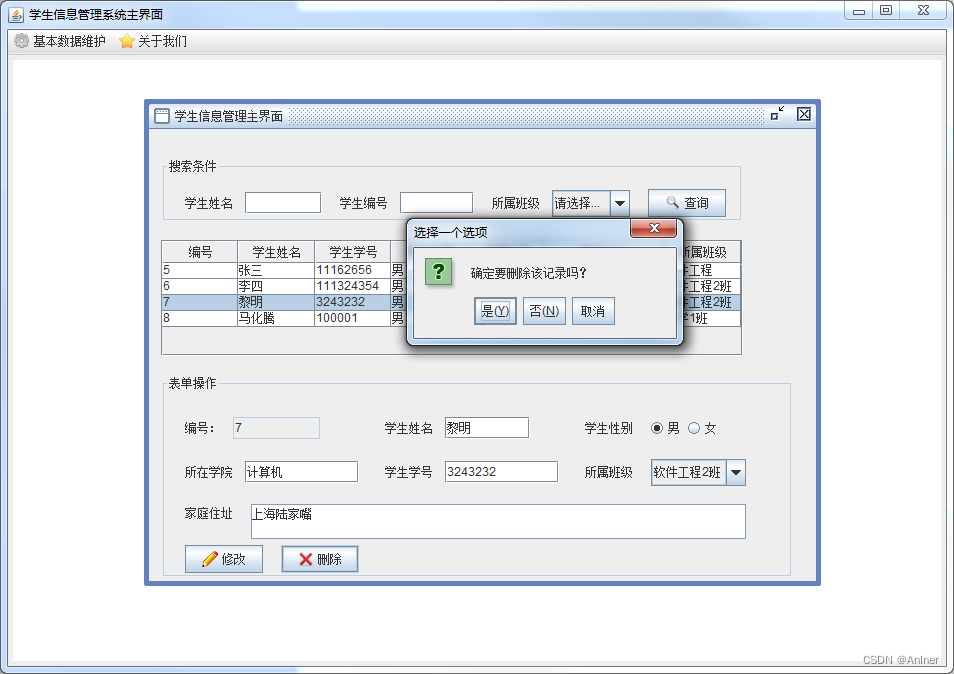
Java课程设计:基于swing的学生信息管理系统
文章目录 一、项目介绍二、项目展示三、源码展示四、源码获取 一、项目介绍 这款Java swing实现的学生信息管理系统和jsp版本的功能很相似,简单的实现了班级信息的增删改查,学生信息的增删改查,数据库采用的是mysql,jdk版本不限&…...

【代码】3d->video
mesh->video import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib.animation import FuncAnimation import matplotlib.animation as animation from pywavefront import Wavefront import osnamedog # 读取OBJ文…...
算法01 递推算法及相关问题详解【C++实现】
目录 递推的概念 训练:斐波那契数列 解析 参考代码 训练:上台阶 参考代码 训练:信封 解析 参考代码 递推的概念 递推是一种处理问题的重要方法。 递推通过对问题的分析,找到问题相邻项之间的关系(递推式&a…...
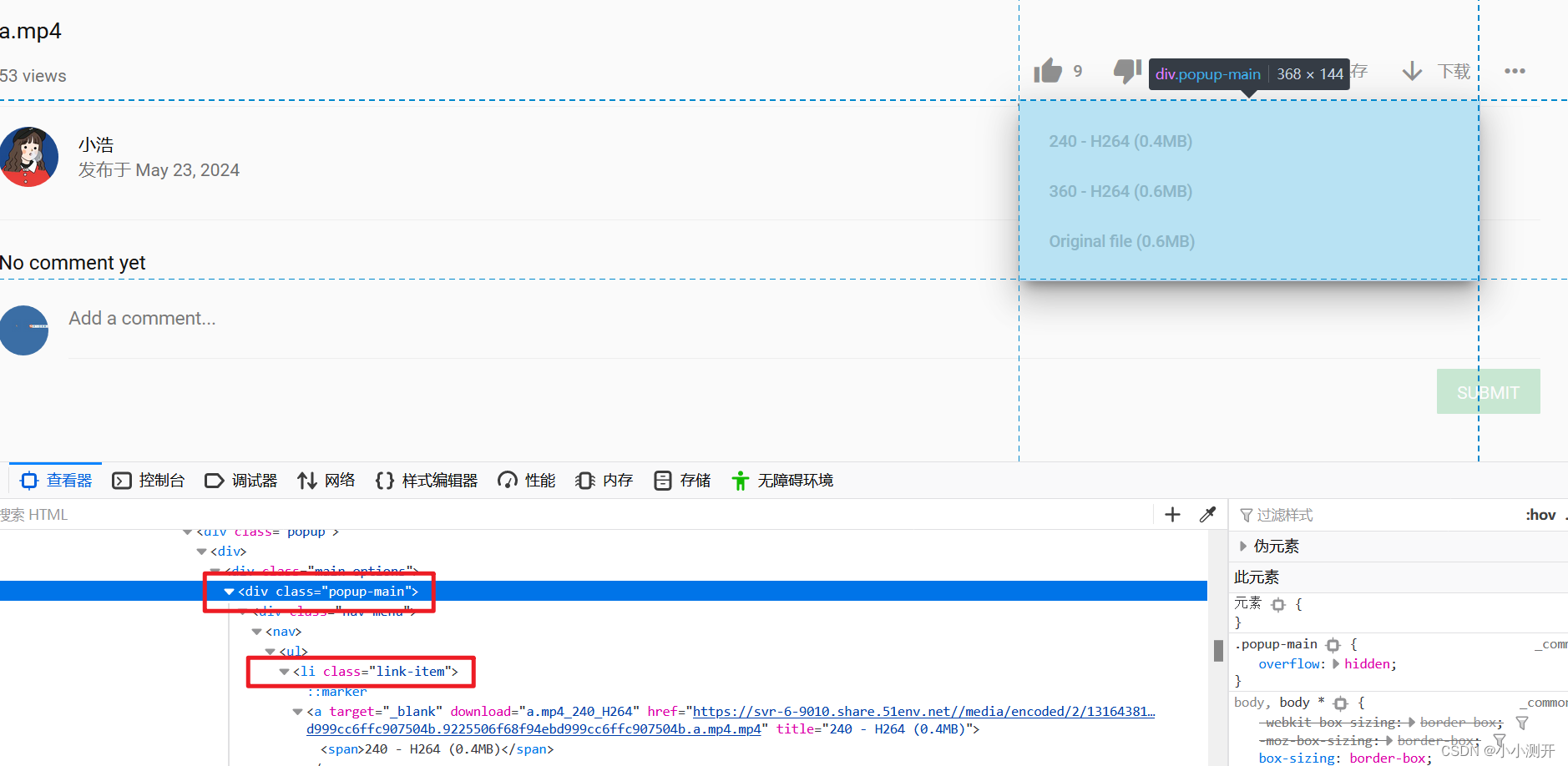
自动化测试火狐下载文件
本篇文章介绍selenium中火狐浏览器如何下载文件。比如我想把这个MP4的视频文件下载下来。 点击之后查看下载的类型是video/mp4 指定使用火狐浏览器 profile webdriver.FirefoxOptions() # 设置firefox默认的下载路径,0表示桌面,1表示我的下载…...
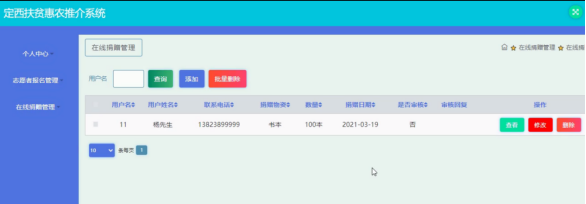
基于JSP技术的定西扶贫惠农推介系统
开头语:你好呀,我是计算机学长猫哥!如果有相关需求,文末可以找到我的联系方式。 开发语言:JSP 数据库:MySQL 技术:B/S架构、JSP技术 工具:Eclipse、MySQL、Tomcat 系统展示 首…...

Linux 终端窗口设置为透明
Linux 终端窗口设置为透明 打开终端 右键鼠标 选择Profile Preferences 点击Background 选择 Transparent background 拖动滑条调整透明度 完成。...

MySQL 中 Varchar(50) 和 varchar(500) 区别是什么?
一. 问题描述 我们在设计表结构的时候,设计规范里面有一条如下规则: 对于可变长度的字段,在满足条件的前提下,尽可能使用较短的变长字段长度。 为什么这么规定?我在网上查了一下,主要基于两个方面 基于存储空间的考…...

强化RAG:微调Embedding还是LLM?
为什么我们需要微调? 微调有利于提高模型的效率和有效性。它可以减少训练时间和成本,因为它不需要从头开始。此外,微调可以通过利用预训练模型的功能和知识来提高性能和准确性。它还提供对原本无法访问的任务和领域的访问,因为它…...

提取 Excel单元格文本下的超链接
在Excel中,可以使用内置的函数来提取单元格中的超链接地址。如果你有一个包含超链接的单元格,例如B1,你可以使用以下步骤来提取这个超链接: 在一个新的单元格(例如C1)中,输入以下公式ÿ…...

一键安全体检!亚信安全携手鼎捷软件推出企业安全体检活动 正式上线
亚信安全联合鼎捷软件股份有限公司(以下简称“鼎捷软件”)正式推出“一键安全体检”服务。亚信安全网络安全专家将携手鼎捷软件数据安全专家,围绕企业的数智安全状况,进行问题探索与治愈、新问题预测与预警,在全面筛查…...
)
numpy - array(1)
一维数据:向量 二位数据:矩阵 维度超过三维的数据:张量 这些数据在numpy中统称array (1)使用穷举法创建多为数据,接受列表或者元组类型的数据 a numpy.array([1, 2, 3]) b numpy.array([[1, 2, 3], (4, 5, 6), [7, 8, 9]]) (2)创建所有元…...
师彼长技以助己(6)递归思维
师彼长技以助己(6)递归思维 递归思维-小游戏 思维小游戏 思维 小游戏:1 玩一个从1或2开始往上加的游戏,谁加到20就赢 如何保证一定赢呢?我们倒推,要先到20的话,谁先到17就赢,如此…...

Kali Linux 2024.2
Kali Linux 2024.2 版本(t64、GNOME 46 和社区包) 比平常晚了一点,但 Kali 2024.2 来了!延迟是由于实现这一目标的幕后变化所致,这也是人们关注的焦点。社区提供了大量帮助,这次他们不仅添加了新的软件包&…...
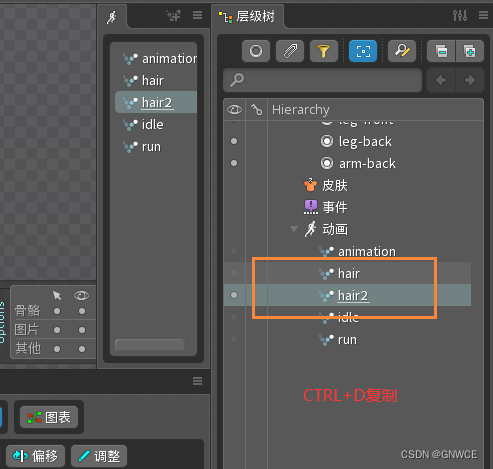
【Spine学习08】之短飘,人物头发动效制作思路
上一节说完了跑步的, 这节说头发发型。 基础过程总结: 1.创建骨骼(头发需要在上方加一个总骨骼) 2.创建网格(并绑定黄线) 3.绑定权重(发根位置的顶点赋予更多总骨骼的权重) 4.切换到…...

chatgpt的命令词
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
