python-求f(x,n)
[题目描述]

输入:
输入 𝑥和 𝑛。
输出:
函数值,保留两位小数。
样例输入1
4.2 10
样例输出1
3.68
来源/分类(难度系数:一星)
完整代码如下:
x,n=map(eval,input().split())
a=1
x1=(x+a)**0.5
while a<n:
a=a+1
x1=(x1+a)**0.5
print("{:.2f}".format(x1))
代码解释:
“x,n= map(eval,input().split()) ”,让用户输入x:既定值和n:终止值。
“a=1
x1=(x+a)**0.5 ”,设定a的初始值为1,令x1=(x+a)**0.5。
“while a<n:
a=a+1
x1=(x1+a)**0.5 ”,当a小于n(终止值)时,使a不断叠加,x1在此基础上不断进行叠代,直至a叠加至a=n(终止值),循环结束。
“print("{:.2f}".format(x1)) ,打印最终结果,并保留两位小数。
运行效果展示:
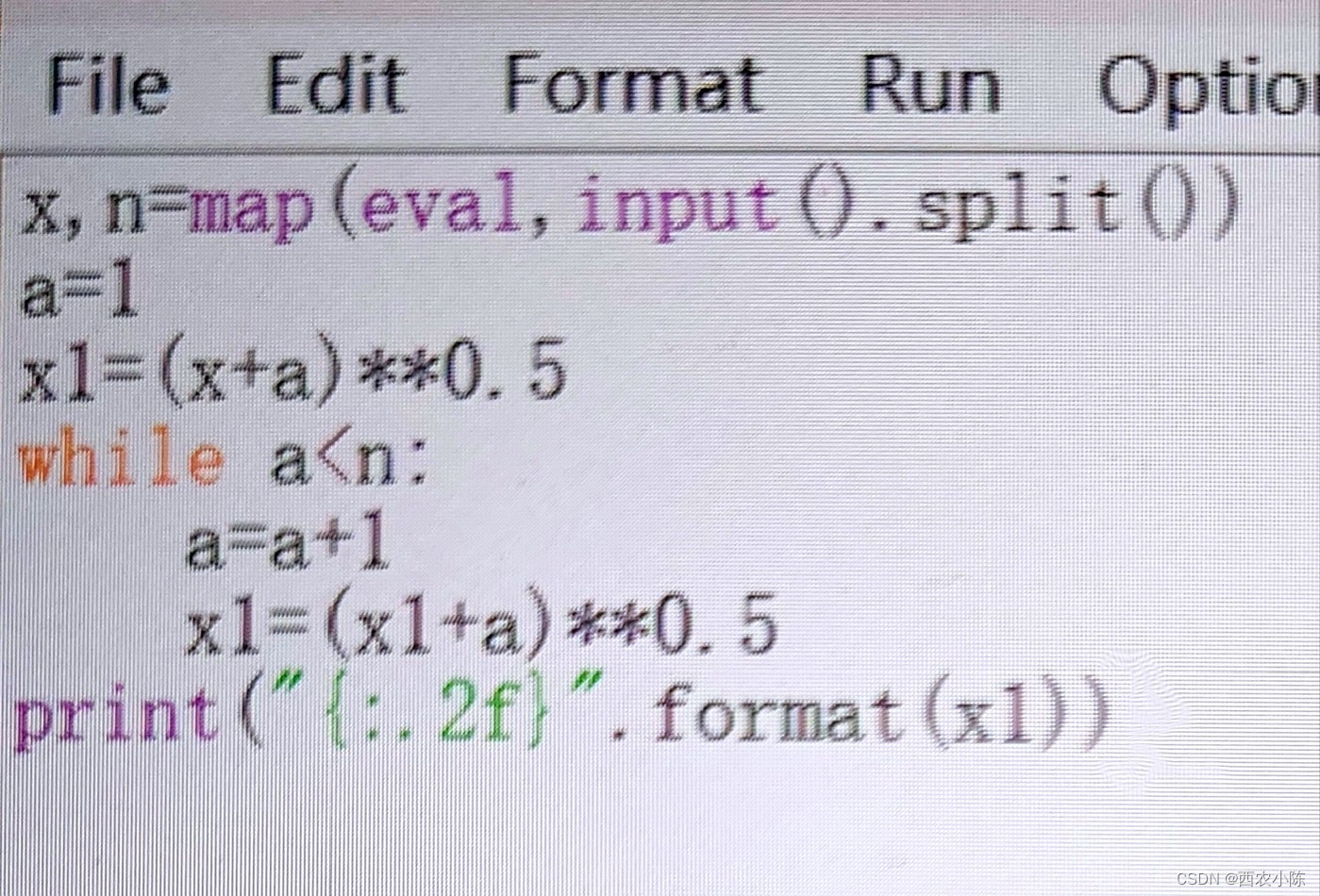

(声明:以上内容均为原创)
相关文章:

python-求f(x,n)
[题目描述] 输入: 输入 𝑥和 𝑛。输出: 函数值,保留两位小数。样例输入1 4.2 10 样例输出1 3.68 来源/分类(难度系数:一星) 完整代码如下: x,nmap(eval,input().split(…...

java值jsp语法笔记
1 JSP注释 1.1 显示注释 显示注释会出现在生成的HTML文档中,对用户可见。 <!-- 这是一个HTML显示注释 --> 1.2 隐式注释 隐式注释不会出现在生成的HTML文档中,对用户不可见。 <%-- 这是一个JSP隐式注释 --%> 2 JSP脚本元素 2.1 局部…...
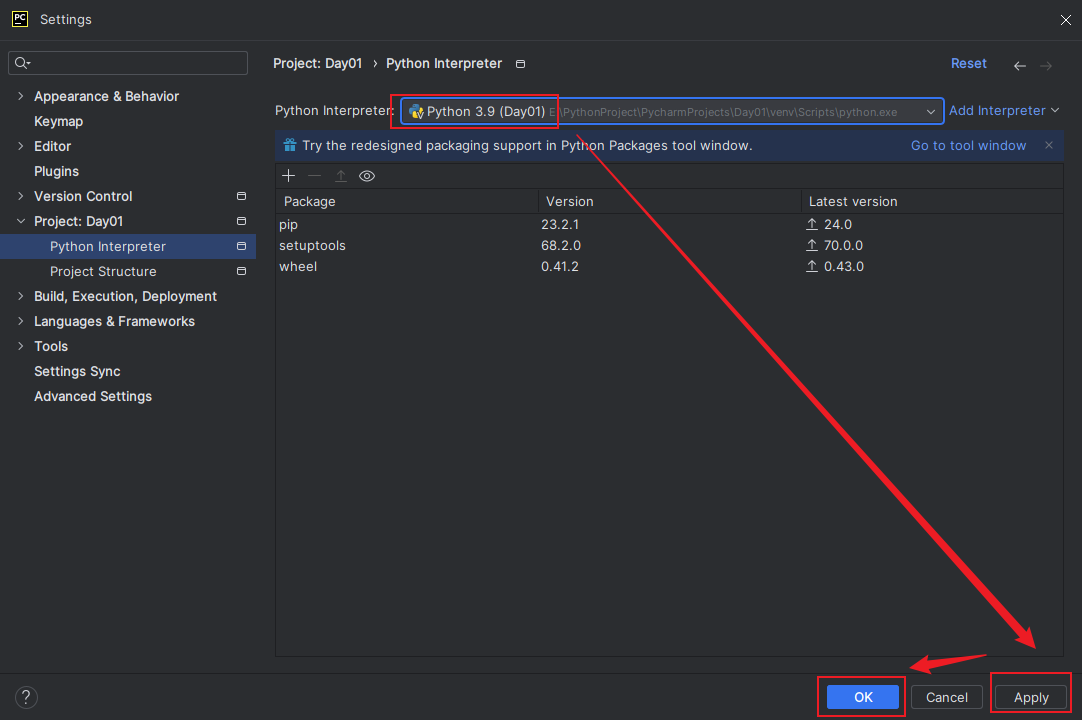
057、PyCharm 运行代码报错:Error Please select a valid Python interpreter
当我们在PyCharm运行代码时,提示如下图错误: 那么问题通常是由于PyCharm未正确配置Python解释器引起的。 我们只需按以下步骤重新配置Python解释器即可: 打开PyCharm设置: 在菜单栏中的点击 “File” -> “Settings”…...
Java实现图书管理系统
一、引言 本篇介绍了一个简易的图书管理系统,面向管理员和普通用户分别给出了不同的菜单,实现了一些基本的图书操作功能,包括图书的增删查改、借阅、归还等 二、图书管理系统框架 图书管理系统,顾名思义,管理的是图…...

使用静态方法接受对象参数
我们先来看一个例子 public class MyInteger { private int value; // 构造函数 public MyInteger(int value) { this.value value; } // 实例方法 public boolean isEven() { return value % 2 0; } // 静态方法接受int参数 public static boolean isEvenStatic…...

cocos creator如何使用cryptojs加解密(及引入方法)
cocos creator如何使用cryptojs加解密(及引入方法) 如果想转请评论留个言并注明原博 Sclifftop 13805064305 阿浚 cocos creator如何使用cryptojs加解密(及引入方法) 步骤 获取库 1. npm install crypto-js -g,加不加…...
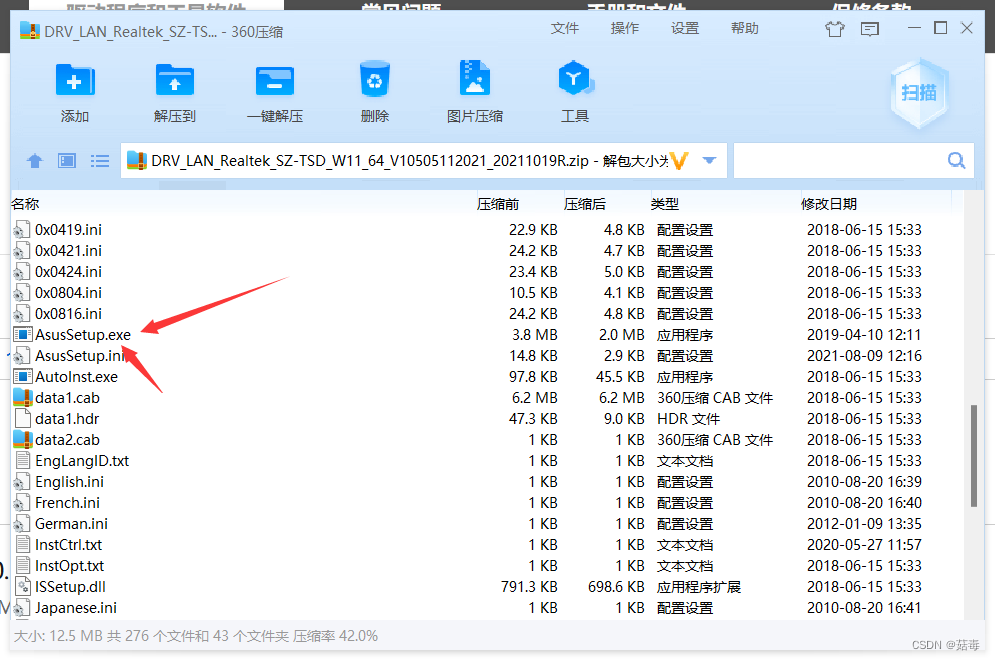
安装台式电脑网卡驱动
安装电脑网卡驱动 1. 概述2. 具体方法2.1 先确定主板型号2.2 详细操作步骤如下2.2.1 方法一2.2.2 方法二2.2 主流主板官网地址 结束语 1. 概述 遇到重装系统后、或者遇到网卡驱动出现问题没有网络时,当不知道怎么办时,以下的方法,可以作为一…...
)
JavaEE-多线程(1)
这篇文章,我们将介绍进程、线程的相关概念以及进程和线程的区别,下篇文章我们将使用Java来编写多线程的代码 进程: 进程(Process)是操作系统中资源分配的基本单位,它是一个正在运行的程序的实例。进程包括…...

【计算机视觉】人脸算法之图像处理基础知识(五)
图像的几何变换 3.图像的旋转 图像的旋转就是让图像按照某一点旋转到指定的角度。需要确定3个参数:图像的旋转中心、旋转角度和缩放因子。在openv中通过getRotationMatrix2D()函数来实现图像的旋转。 import cv2 import numpy as npimgpath "images/img1.j…...

工业 web4.0 的 UI 风格,独树一帜
工业 web4.0 的 UI 风格,独树一帜...

BSP驱动教程-CAN/CANFD/CANopen知识点总结分享
学习知识点整理: CAN 总线的前世今生: https://www.armbbs.cn/forum.php?modviewthread&tid104480 wikibai百科CAN总线: https://en.wikipedia.org/wiki/CAN_bus 瑞萨CAN入门教程: https://www.armbbs.cn/forum.php?m…...

微服务之远程调用
常见的远程调用方式 RPC:Remote Produce Call远程过程调用,类似的还有 。自定义数据格式,基于原生TCP通信,速度快,效率高。早期的webservice,现在热门的dubbo (12不再维护、17年维护权交给apac…...
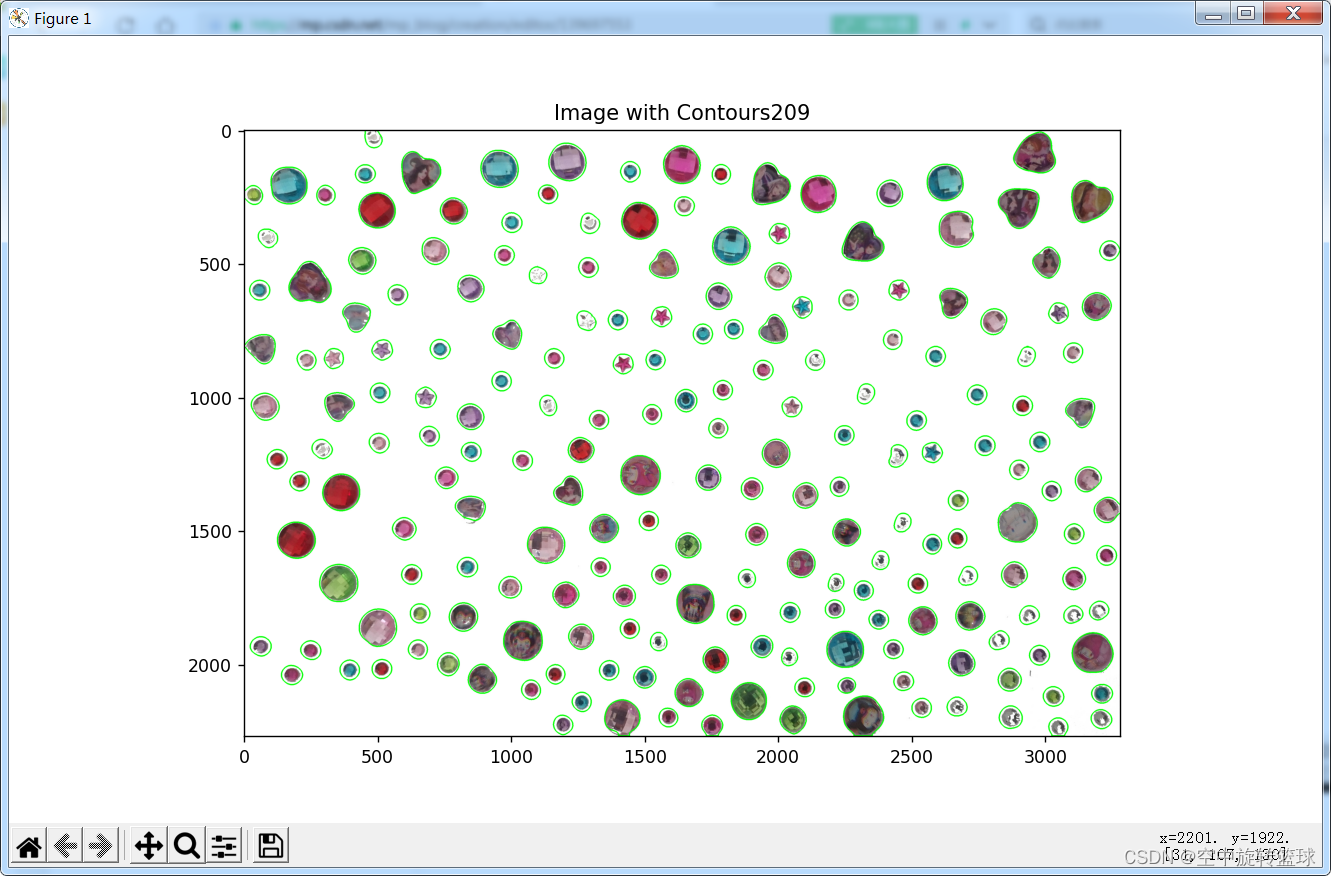
Opencv数一数有多少个水晶贴纸?
1.目标-数出有多少个贴纸 好久没更新博客了,最近家里小朋友在一张A3纸上贴了很多水晶贴纸,要让我帮他数有多少个,看上去有点多,贴的也比较随意,于是想着使用Opencv来识别一下有多少个。 原图如下: 代码…...

AI Agent智能应用从0到1定制开发(完结)
在数字化时代的浪潮中,人工智能(AI)代理智能应用如同星辰般璀璨,引领着技术革新的潮流。从零开始定制开发一款AI Agent智能应用,就像是在无垠的宇宙中绘制一颗新星的轨迹,每一步都充满了挑战与创新的火花。…...

事件驱动架构:新时代的软件设计范式
引言 在现代软件开发中,随着系统复杂度的增加和实时响应需求的提升,传统的单体架构和同步调用模型逐渐显露出其局限性。事件驱动架构(Event-Driven Architecture, EDA)作为一种高度解耦、灵活性强的架构设计模式,越来…...

【机器学习】机器学习与物流科技在智能配送中的融合应用与性能优化新探索
文章目录 引言机器学习与物流科技的基本概念机器学习概述监督学习无监督学习强化学习 物流科技概述路径优化车辆调度需求预测 机器学习与物流科技的融合应用实时物流数据分析数据预处理特征工程 路径优化与优化模型训练模型评估 车辆调度与优化深度学习应用 需求预测与优化强化…...

web前端何去何从:探索未来之路
web前端何去何从:探索未来之路 在数字化浪潮的推动下,web前端技术正经历着前所未有的变革。随着新技术的不断涌现和用户体验的持续提升,web前端开发者们面临着前所未有的挑战与机遇。那么,web前端究竟何去何从?本文将…...

yolov8通过训练完成的模型生成图片热力图--论文需要
源代码来自于网络 使用pytorch_grad_cam,对特定图片生成热力图结果。 安装热力图工具 pip install pytorch_grad_cam pip install grad-cam# get_params中的参数: # weight: # 模型权重文件,代码默认是yolov8m.pt # c…...
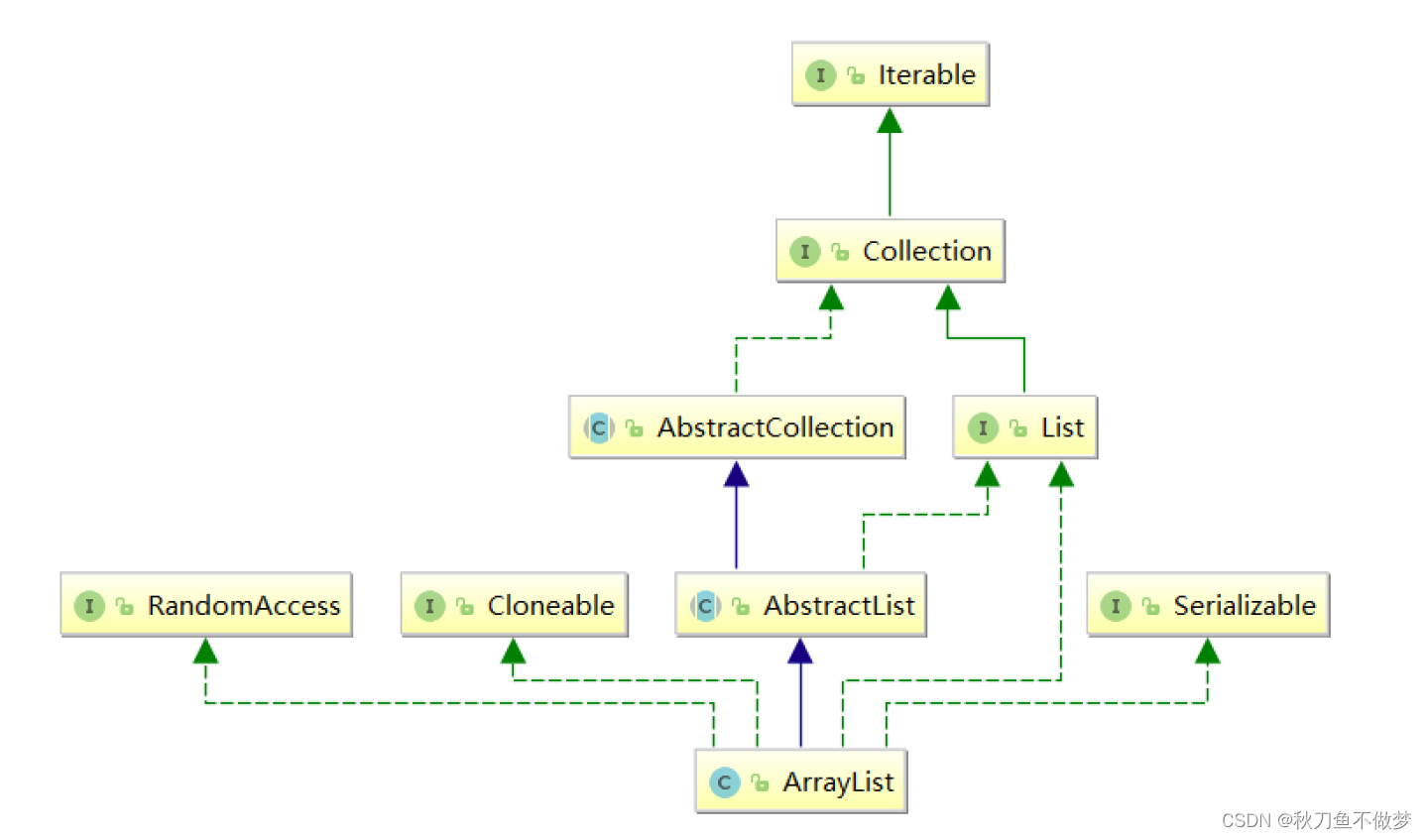
Java数据结构之ArrayList(如果想知道Java中有关ArrayList的知识点,那么只看这一篇就足够了!)
前言:ArrayList是Java中最常用的动态数组实现之一,它提供了便捷的操作接口和灵活的扩展能力,使得在处理动态数据集合时非常方便。本文将深入探讨Java中ArrayList的实现原理、常用操作以及一些使用场景。 ✨✨✨这里是秋刀鱼不做梦的BLOG ✨✨…...
Zadig vs. Jenkins 详细比较
01、Zadig vs. Jenkins:关于时代的选择 最近官方公众号发布了一篇名为 《是时候和 Jenkins 说再见了》的文章,引起了社区的广泛关注和讨论。作为曾经最被广泛使用的持续构建交付工具,Jenkins 的江湖地位似乎被挑战了。评论中有一条被高度点赞…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
