动态规划之股票问题大总结
参考资料:代码随想录 (programmercarl.com)
一、只能买卖一次
题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode)
算法思想:
设置两种状态:0表示已持有股票,1表示未持有股票
1.dp[i][0]表示第i天已持有股票时,获得的最大利润
dp[i][1]表示第i天未持有股票时,获得的最大利润
2.递推式:
对于dp[i][0]:
若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];
若第i-1天未持有股票,则dp[i][0]=0-prices[i];
综上,dp[i][0]=fmax(dp[i-1][0],-prices[i]);
对于dp[i][1]:
若第i-1天未持有股票,则dp[i][1]=dp[i-1][1];
若第i-1天已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];
综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);
3.初始化:
dp[0][0]=-prices[0];
算法实现:
int maxProfit(int *prices,int pricesSize){//设置两种状态:0表示已持有股票,1表示未持有股票//1.dp[i][0]表示第i天已持有股票时,获得的最大利润//dp[i][1]表示第i天未持有股票时,获得的最大利润//2.递推式://对于dp[i][0]:// 若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];// 若第i-1天未持有股票,则dp[i][0]=0-prices[i];//综上,dp[i][0]=fmax(dp[i-1][0],-prices[i]);//对于dp[i][1]:// 若第i-1天未持有股票,则dp[i][1]=dp[i-1][1];// 若第i-1天已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];//综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);//3.初始化://dp[0][0]=-prices[0];int dp[pricesSize][2];memset(dp,0,sizeof(dp));dp[0][0]=-prices[0];for(int i=1;i<pricesSize;i++){dp[i][0]=fmax(dp[i-1][0],-prices[i]);dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[pricesSize-1][1];
}二、可以买卖多次
题目链接:122. 买卖股票的最佳时机 II - 力扣(LeetCode)
算法思想:
设置两种状态:0表示已持有股票,1表示未持有股票
1.dp[i][0]表示第i天已持有股票时,获得的最大利润
dp[i][1]表示第i天未持有股票时,获得的最大利润
2.递推式:
对于dp[i][0]:
若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];
若第i-1天未持有股票,则dp[i][0]=dp[i-1][1]-prices[i];
综上,dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);
(II与I的唯一区别就在于:
只允许一次购买时,在持有股票之前,所获得利润必为0,而允许多次购买则不然)
对于dp[i][1]:
若第i-1天未持有股票,则dp[i][1]=dp[i-1][1];
若第i-1天已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];
综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);
3.初始化:
dp[0][0]=-prices[0];
算法实现:
int maxProfitII(int *prices,int pricesSize){//设置两种状态:0表示已持有股票,1表示未持有股票//1.dp[i][0]表示第i天已持有股票时,获得的最大利润//dp[i][1]表示第i天未持有股票时,获得的最大利润//2.递推式://对于dp[i][0]:// 若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];// 若第i-1天未持有股票,则dp[i][0]=dp[i-1][1]-prices[i];//综上,dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);//(II与I的唯一区别就在于:// 只允许一次购买时,在持有股票之前,所获得利润必为0,而允许多次购买则不然)//对于dp[i][1]:// 若第i-1天未持有股票,则dp[i][1]=dp[i-1][1];// 若第i-1天已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];//综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);//3.初始化://dp[0][0]=-prices[0];int dp[pricesSize][2];memset(dp,0,sizeof(dp));dp[0][0]=-prices[0];for(int i=1;i<pricesSize;i++){dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[pricesSize-1][1];
}三、最多买卖两次
题目链接:123. 买卖股票的最佳时机 III - 力扣(LeetCode)
算法思想:
设置四种状态:
0表示第一次已持有股票
1表示第一次未持有股票
2表示第二次已持有股票
3表示第二次未持有股票
1.dp[i][0]表示第i天第一次已持有股票时,获得的最大利润
dp[i][1]表示第i天第一次未持有股票时,获得的最大利润
dp[i][2]表示第i天第二次已持有股票时,获得的最大利润
dp[i][3]表示第i天第二次未持有股票时,获得的最大利润
2.递推式:
对于dp[i][0]:
若第i-1天第一次已持有股票,则dp[i][0]=dp[i-1][0];
若第i-1天第一次未持有股票,则dp[i][0]=0-prices[i];
综上,dp[i][0]=fmax(dp[i-1][0],-prices[i]);
对于dp[i][1]:
若第i-1天第一次未持有股票,则dp[i][1]=dp[i-1][1];
若第i-1天第一次已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];
综上,dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);
对于dp[i][2]:
若第i-1天第一次已持有股票,则dp[i][2]=dp[i-1][2];
若第i-1天第一次未持有股票,则dp[i][2]=dp[i-1][1]-prices[i];
综上,dp[i][2]=fmax(dp[i-1][2],dp[i-1][1]-prices[i]);
对于dp[i][3]:
若第i-1天第一次未持有股票,则dp[i][3]=dp[i-1][3];
若第i-1天第一次已持有股票,则dp[i][3]=dp[i-1][2]+prices[i];
综上:dp[i][3]=fmax(dp[i-1][3],dp[i-1][2]+prices[i]);
3.初始化:
dp[0][0]=dp[0][2]=-prices[0];
算法实现:
int maxProfitIII(int *prices,int pricesSize){//设置四种状态:// 0表示第一次已持有股票// 1表示第一次未持有股票// 2表示第二次已持有股票// 3表示第二次未持有股票//1.dp[i][0]表示第i天第一次已持有股票时,获得的最大利润//dp[i][1]表示第i天第一次未持有股票时,获得的最大利润//dp[i][2]表示第i天第二次已持有股票时,获得的最大利润//dp[i][3]表示第i天第二次未持有股票时,获得的最大利润//2.递推式://对于dp[i][0]:// 若第i-1天第一次已持有股票,则dp[i][0]=dp[i-1][0];// 若第i-1天第一次未持有股票,则dp[i][0]=0-prices[i];//综上,dp[i][0]=fmax(dp[i-1][0],-prices[i]);//对于dp[i][1]:// 若第i-1天第一次未持有股票,则dp[i][1]=dp[i-1][1];// 若第i-1天第一次已持有股票,则dp[i][1]=dp[i-1][0]+prices[i];//综上,dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);//对于dp[i][2]:// 若第i-1天第一次已持有股票,则dp[i][2]=dp[i-1][2];// 若第i-1天第一次未持有股票,则dp[i][2]=dp[i-1][1]-prices[i];//综上,dp[i][2]=fmax(dp[i-1][2],dp[i-1][1]-prices[i]);//对于dp[i][3]:// 若第i-1天第一次未持有股票,则dp[i][3]=dp[i-1][3];// 若第i-1天第一次已持有股票,则dp[i][3]=dp[i-1][2]+prices[i];//综上:dp[i][3]=fmax(dp[i-1][3],dp[i-1][2]+prices[i]);//3.初始化://dp[0][0]=dp[0][2]=-prices[0];int dp[pricesSize][4];memset(dp,0,sizeof(dp));dp[0][0]=dp[0][2]=-prices[0];for(int i=1;i<pricesSize;i++){dp[i][0]=fmax(dp[i-1][0],-prices[i]);dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]);dp[i][2]=fmax(dp[i-1][2],dp[i-1][1]-prices[i]);dp[i][3]=fmax(dp[i-1][3],dp[i-1][2]+prices[i]);}return dp[pricesSize-1][3];
}四、最多买卖k次
题目链接:188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
算法思想:
设置2*k种状态:
for j=1 to k
2*j-1表示第j次已持有股票
2*j+1表示第j次未持有股票
1.dp[i][2*j-1]表示第i天第j次已持有股票时,获得的最大利润
dp[i][2*j]表示第i天第j次未持有股票时,获得的最大利润
2.递推式:
对于dp[i][2*j-1]:
若第i-1天第j次已持有股票,则dp[i][2*j-1]=dp[i-1][2*j-1];
若第i-1天第j次未持有股票,则dp[i][2*j-1]=dp[i-1][2*j-2]-prices[i];
综上,dp[i][2*j-1]=fmax(dp[i-1][2*j-1],dp[i-1][2*j-2]-prices[i]);
对于dp[i][2*j]:
若第i-1天第j次未持有股票,则dp[i][2*j]=dp[i-1][2*j];
若第i-1天第j次已持有股票,则dp[i][2*j]=dp[i-1][2*j-1]+prices[i];
综上,dp[i][2*j]=fmax(dp[i-1][2*j],dp[i-1][2*j-1]+prices[i]);
3.初始化:
for(int i=1;i<=2*k;i+=2) dp[0][i]=-prices[0];
算法实现:(实际上就是在三的基础上,从2次买卖延伸到了k次买卖,用for循环即可)
int maxProfitIV(int k,int *prices,int pricesSize){//设置2*k种状态:// for j=1 to k// 2*j-1表示第j次已持有股票// 2*j+1表示第j次未持有股票//1.dp[i][2*j-1]表示第i天第j次已持有股票时,获得的最大利润//dp[i][2*j]表示第i天第j次未持有股票时,获得的最大利润//2.递推式://对于dp[i][2*j-1]:// 若第i-1天第j次已持有股票,则dp[i][2*j-1]=dp[i-1][2*j-1];// 若第i-1天第j次未持有股票,则dp[i][2*j-1]=dp[i-1][2*j-2]-prices[i];//综上,dp[i][2*j-1]=fmax(dp[i-1][2*j-1],dp[i-1][2*j-2]-prices[i]);//对于dp[i][2*j]:// 若第i-1天第j次未持有股票,则dp[i][2*j]=dp[i-1][2*j];// 若第i-1天第j次已持有股票,则dp[i][2*j]=dp[i-1][2*j-1]+prices[i];//综上,dp[i][2*j]=fmax(dp[i-1][2*j],dp[i-1][2*j-1]+prices[i]);//3.初始化://for(int i=1;i<=2*k;i+=2) dp[0][i]=-prices[0];int dp[pricesSize][2*k+1];memset(dp,0,sizeof(dp));for(int i=1;i<=2*k;i+=2)dp[0][i]=-prices[0];for(int i=1;i<pricesSize;i++){for(int j=1;j<=k;j++){dp[i][2*j-1]=fmax(dp[i-1][2*j-1],dp[i-1][2*j-2]-prices[i]);dp[i][2*j]=fmax(dp[i-1][2*j],dp[i-1][2*j-1]+prices[i]);}}return dp[pricesSize-1][2*k];
}五、买卖多次,卖出有一天冷冻期
题目链接:309. 最佳买卖股票时机含冷冻期 - 力扣(LeetCode)
算法思想:
设置三种状态:
0表示已持有股票
1表示未持有股票且处于非冷冻状态
2表示未持有股票且处于冷冻状态
1.dp[i][0]表示第i天已持有股票时,获得的最大利润
dp[i][1]表示第i天未持有股票且处于非冷冻状态时,获得的最大利润
dp[i][2]表示第i天未持有股票且处于冷冻状态时,获得的最大利润
2.递推式:
对于dp[i][0]:
若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];
若第i-1天未持有股票,必为非冷冻状态,则dp[i][0]=dp[i-1][1]-prices[i];
综上,dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);
对于dp[i][1]:
第i-1天必未持有股票
若第i-1天未持有股票且处于非冷冻状态,则dp[i][1]=dp[i-1][1];
若第i-1天未持有股票且处于冷冻状态,则dp[i][1]=dp[i-1][2];
综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][2]);
对于dp[i][2]:
第i-1天必已持有股票,则dp[i][2]=dp[i-1][0]+prices[i];
3.初始化:
dp[0][0]=-prices[0];
算法实现:
int maxProfitV(int *prices,int pricesSize){//设置三种状态:// 0表示已持有股票// 1表示未持有股票且处于非冷冻状态// 2表示未持有股票且处于冷冻状态//1.dp[i][0]表示第i天已持有股票时,获得的最大利润//dp[i][1]表示第i天未持有股票且处于非冷冻状态时,获得的最大利润//dp[i][2]表示第i天未持有股票且处于冷冻状态时,获得的最大利润//2.递推式://对于dp[i][0]:// 若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];// 若第i-1天未持有股票,必为非冷冻状态,则dp[i][0]=dp[i-1][1]-prices[i];//综上,dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);//对于dp[i][1]:// 第i-1天必未持有股票// 若第i-1天未持有股票且处于非冷冻状态,则dp[i][1]=dp[i-1][1];// 若第i-1天未持有股票且处于冷冻状态,则dp[i][1]=dp[i-1][2];//综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][2]);//对于dp[i][2]:// 第i-1天必已持有股票,则dp[i][2]=dp[i-1][0]+prices[i];//3.初始化://dp[0][0]=-prices[0];int dp[pricesSize][3];memset(dp,0,sizeof(dp));dp[0][0]=-prices[0];for(int i=1;i<pricesSize;i++){dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=fmax(dp[i-1][1],dp[i-1][2]);dp[i][2]=dp[i-1][0]+prices[i];}return fmax(dp[pricesSize-1][1],dp[pricesSize-1][2]);
}六、买卖多次,卖出有手续费
题目链接:714. 买卖股票的最佳时机含手续费 - 力扣(LeetCode)
算法思想:(同二)
算法实现:(如果掌握了二,那么这题就不用看)
int maxProfitVI(int *prices,int pricesSize,int fee){//设置两种状态:0表示已持有股票,1表示未持有股票//1.dp[i][0]表示第i天已持有股票时,获得的最大利润//dp[i][1]表示第i天未持有股票时,获得的最大利润//2.递推式://对于dp[i][0]:// 若第i-1天已持有股票,则dp[i][0]=dp[i-1][0];// 若第i-1天未持有股票,则dp[i][0]=dp[i-1][1]-prices[i];//综上,dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);//对于dp[i][1]:// 若第i-1天未持有股票,则dp[i][1]=dp[i-1][1];// 若第i-1天已持有股票,则dp[i][1]=dp[i-1][0]+prices[i]-fee;//综上:dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]-fee);//3.初始化://dp[0][0]=-prices[0];int dp[pricesSize][2];memset(dp,0,sizeof(dp));dp[0][0]=-prices[0];for(int i=1;i<pricesSize;i++){dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]-fee);}return dp[pricesSize-1][1];
}相关文章:

动态规划之股票问题大总结
参考资料:代码随想录 (programmercarl.com)一、只能买卖一次题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode)算法思想:设置两种状态:0表示已持有股票,1表示未持有股票1.dp[i][0]表示第i天已持有股票时&…...

我来跟你讲vue进阶
一、组件(重点) 组件(Component)是 Vue.js 最强大的功能之一。 组件可以扩展 HTML 元素,封装可重用的代码。 组件系统让我们可以用独立可复用的小组件来构建大型应用,几乎任意类型的应用的界面都可以抽象…...
E. Vlad and a Pair of Numbers)
#847(Div3)E. Vlad and a Pair of Numbers
原题链接: E. Vlad and a Pair of Numbers 题意: 题目有公式 a⊕b(ab)/2xa ⊕ b (a b) / 2 xa⊕b(ab)/2x, 给你的是 xxx,让输出一组满足题目要求的 a,ba,ba,b,没有就输出−1-1…...
怎么把pdf转换成图片?这个方法你值得拥有
想要高效率的工作,除了需要大家合理安排时间之外,一些能够辅助高效工作的工具也是必不可少的。就拿要把一份pdf文件转换成若干图片来说,如果不知道方法,找不到合适的转换工具,那么想要完成这一任务,势必要花…...

go语言使用append向二维数组添加一维数组
var ans [][]int ans append(ans, append([]int(nil), nums...))(正确写法)需要注意的是,为了避免对原切片造成影响,代码在将当前排列追加到结果数组 ans 时,使用了 append(ans, append([]int(nil), nums…)) 的方式…...

YOLOv5训练大规模的遥感实例分割数据集 iSAID从切图到数据集制作及训练
最近想训练遥感实例分割,纵观博客发现较少相关 iSAID数据集的切分及数据集转换内容,思来想去应该在繁忙之中抽出时间写个详细的教程。 iSAID数据集下载 iSAID数据集链接 下载上述数据集。 百度网盘中的train和val中包含了实例和语义分割标签。 上述…...
)
js学习5(函数)
目录 定义函数 函数的特性 使用函数模拟类 模拟私有属性和方法 闭包 函数特性利用 箭头函数 定义函数 function func1(name) { console.log(name); } func2 function (name) { console.log(name); } func3 function func0(name) { console.log(name); } co…...

用Qt画一个仪表盘
关于Qt Qt是一个跨平台的C图形用户界面应用程序框架,通过使用Qt,可以快速开发出跨平台的多平台应用程序,包括Windows、Mac OS X、Linux和其他Unix系统。Qt提供了强大的图形操作界面(GUI)程序开发和移植的能力…...
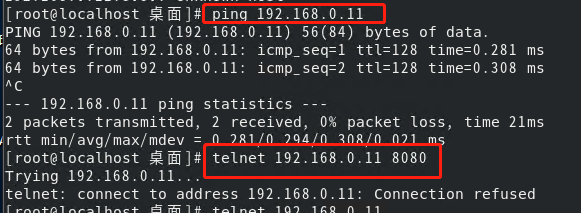
linux 端口查询命令
任何知识都是用进废退,有段时间没摸linux,这大脑里的知识点仿佛全部消失了,就无语。 索性,再写一篇记录,加强一下记忆,下次需要就看自己的资料好了。lsof命令Linux端口查询命令可以通过lsof实现:…...

C语言函数: 字符串函数及模拟实现strtok()、strstr()、strerror()
C语言函数: 字符串函数及模拟实现strtok()、strstr()、strerror() strstr()函数: 作用:字符串查找。在一串字符串中,查找另一串字符串是否存在。 形参: str2在str1中寻找。返回值是char*的指针 原理:如果在str1中找到了str2&…...

【学习笔记】人工智能哲学研究:《心智、语言和机器》
关于人工智能哲学,我曾在这篇文章里 【脑洞大开】从哲学角度看人工智能:介绍徐英瑾的《心智、语言和机器》 做过介绍。图片来源:http://product.dangdang.com/29419969.html在我完成了一些人工智能相关的工作以后,我再来分享《心智…...
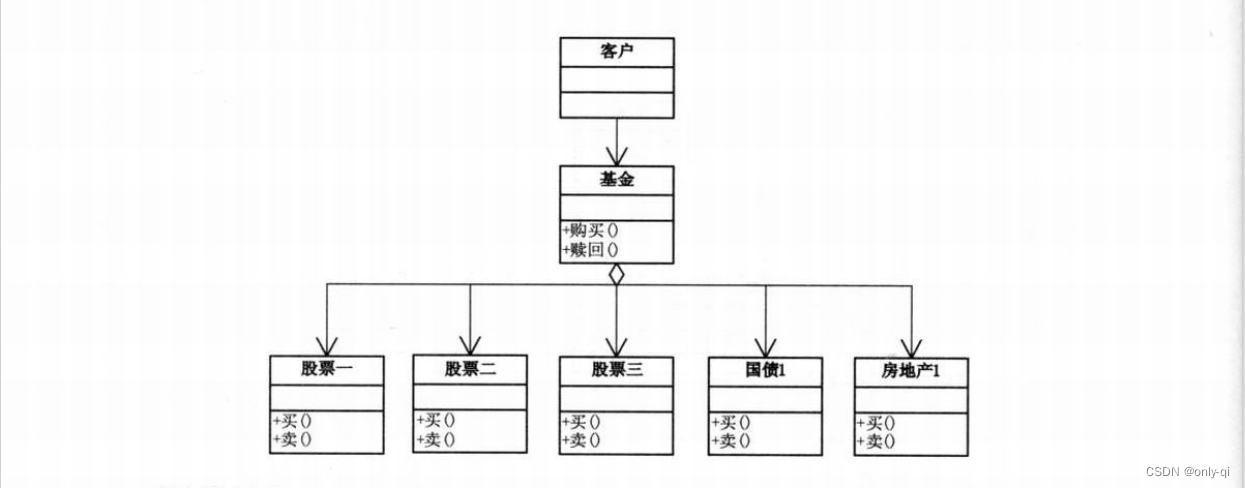
设计模式之门面模式(外观模式)
目录 1.模式定义 2.应用场景 2.1 电源总开关例子 2.2 股民炒股场景 编辑 3. 实例如下 4. 门面模式的优缺点 传送门: 项目中用到的责任链模式 给对象讲工厂模式,必须易懂易会 策略模式,工作中你用上了吗? 1.模式定…...
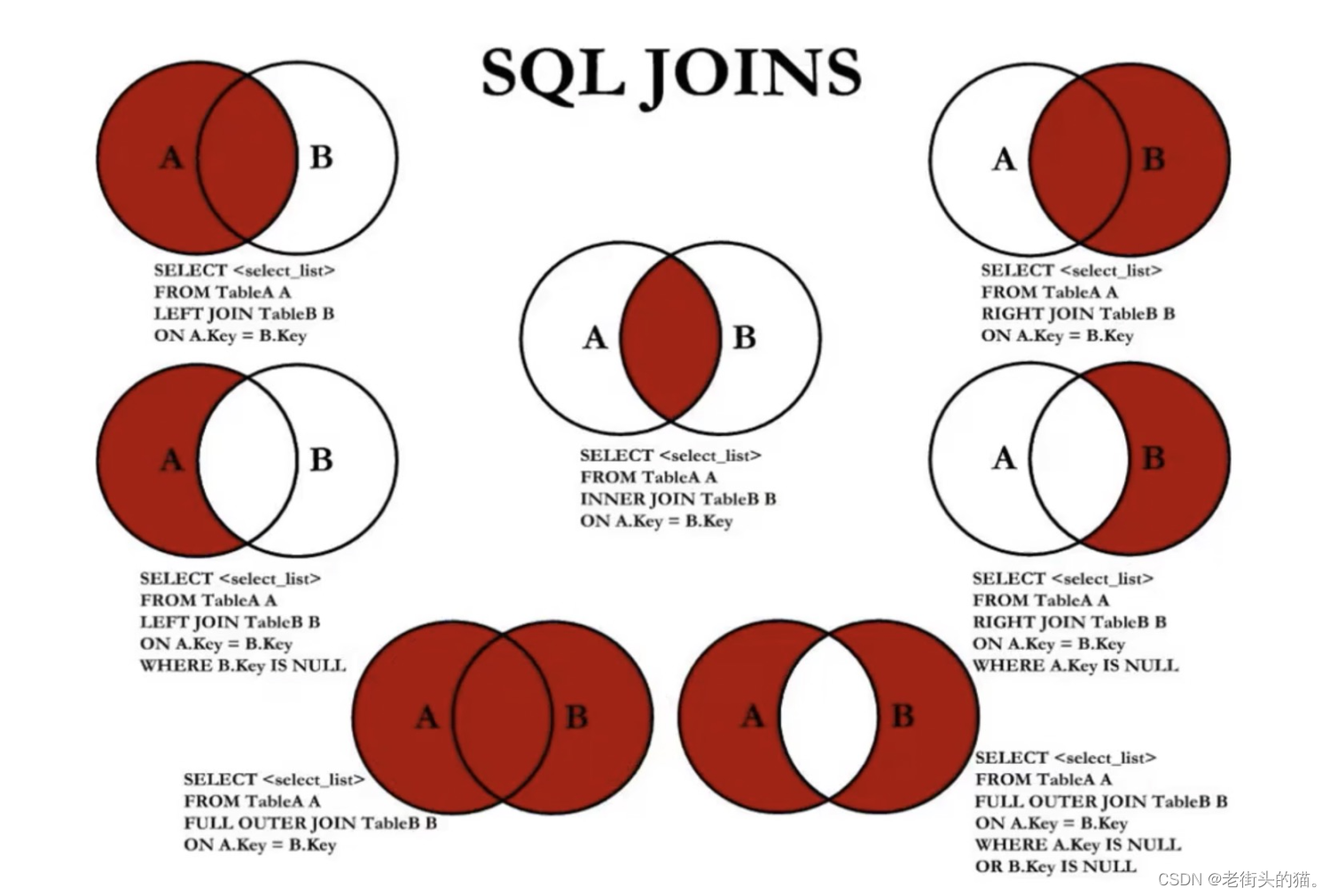
MySQL - 多表查询
目录1. 多表查询示例2. 多表查询分类2.1 等/非等值连接2.1.1 等值连接2.1.2非等值连接2.2 自然/非自然连接2.3 内/外连接2.3.1 内连接2.3.2 外连接3.UNION的使用3.1 合并查询结果3.1.1 UNION操作符3.1.2 UNION ALL操作符4. 7种JOIN操作5. join 多张表多表查询,也称为…...

自定义报表是什么?
自定义报表是指根据用户的需求和要求,自行设计和生成的报表。自定义报表可以根据用户的具体需求,选择需要的数据和指标,进行灵活的排列和组合,生成符合用户要求的报表。自定义报表可以帮助用户更好地了解业务情况,发现…...

windows安装docker-小白用【避坑】【伸手党福利】
目录实操开启 Hyper-V 和容器特性下载docker安装dockercmd中,使用命令测试是否成功报错解决办法:下载linux模拟器wsl:双击打开docker重新打开cmd,输入命令,成功显示sever和clinet实操 开启 Hyper-V 和容器特性 控制面…...
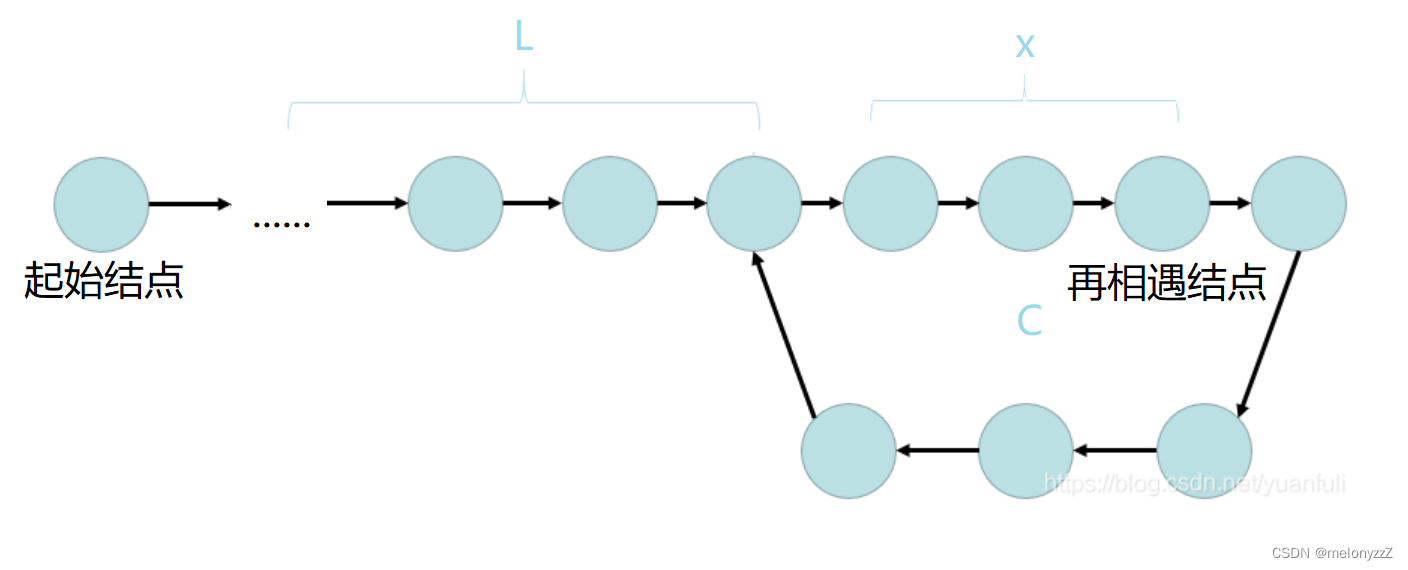
环形链表相关的练习
目录 一、相交链表 二、环形链表 三、环形链表 || 一、相交链表 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 图示两个链表在节点 c1 开始相交: 题目数据…...

C++ 提示对话框
头文件 #include<iostream>#include<cstdio> using namespace std; 函数格式 MessageBox( HWND hWnd, LPCTSTR lpText, LPCTSTR lpCaption, UINT uType) 参数 hWnd :此参数代表消息框拥有的窗口。如果为NULL,则消息框没有拥有窗口。 lp…...
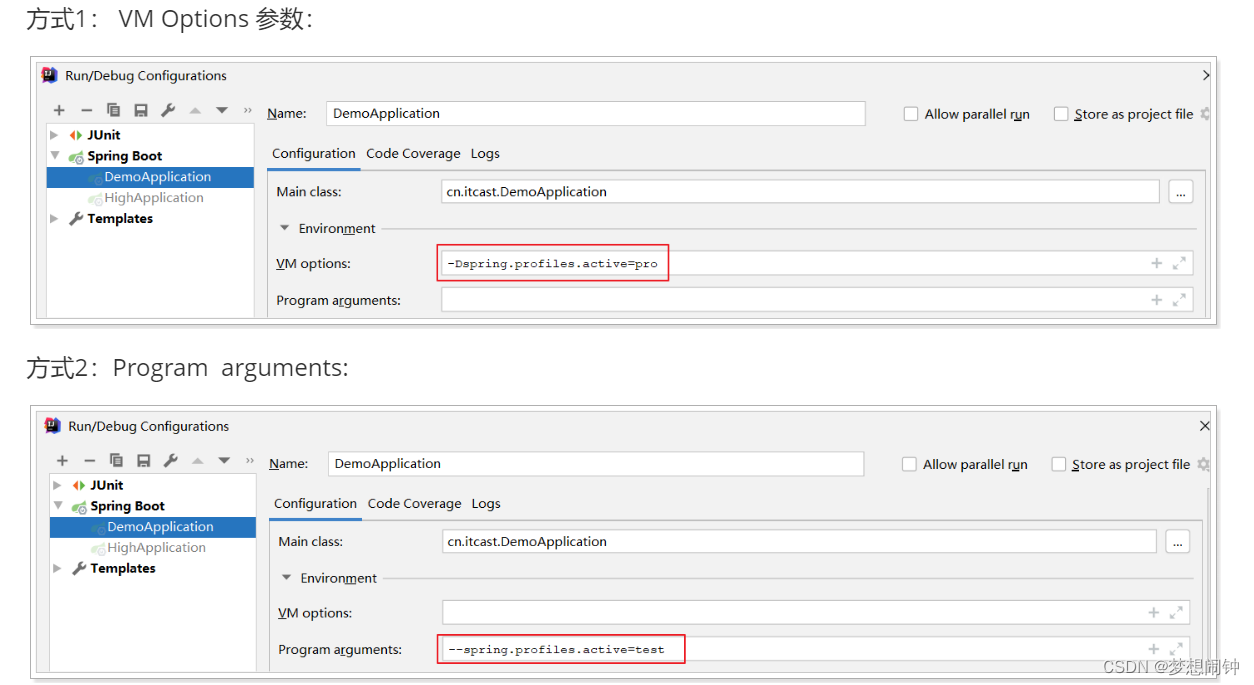
SprintBoot打包及profile文件配置
打成Jar包 需要添加打包组件将项目中的资源、配置、依赖包打到一个jar包中,可以使用maven的package;运行: java -jar xxx(jar包名) 操作步骤 第一步: 引入Spring Boot打包插件 <!--打包的插件--> <build><!--修改jar的名字--><fi…...

java面试-java集合
说说你如何选用集合? 需要键值对选用 map 接口下的集合,需要排序用 TreeMap, 不需要排序用 HashMap 不需要键值对仅存放元素则选择 Collection 下实现的接口,保证元素唯一使用 Set, 不需要则选用 List Collection 和 Collections 有什么区别…...

Node.js简介
客户端访问网页时向服务器端发送请求要访问服务器中的页面,服务器收到请求后向数据库中进行搜索,搜索到相关数据然后返回结果给客户端显示; 这个过程就类似于:客人(客户端)去饭馆(服务端&#…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
