从0开发一个Chrome插件：项目实战——广告拦截插件
相关文章：
从0开发一个Chrome插件：项目实战——广告拦截插件
前言 这是《从0开发一个Chrome插件》系列的第十七篇文章，本系列教你如何从0去开发一个Chrome插件，每篇文章都会好好打磨，写清楚我在开发过程遇到的问题，还有开发经验和技巧。 专栏： 从0开发一个Chrome插件：什么是Chrome插件？从0开发一个Chrome插件：开发Chrome插件的必…...
C++ 32 之 静态成员函数
#include <iostream> #include <string> using namespace std;// 特点: // 1.在编译阶段就分配了内存空间 // 2.类内声明，在类外进行初始化 // 3.所有对象共享一份静态成员数据 class Students02{ public:int s_c;static int s_d;// 静态成员函数&#…...
Python闯LeetCode--第1题：两数之和
Problem: 1. 两数之和 文章目录 思路解题方法复杂度Code 思路 看到这道题第一思路就是暴力破解，枚举，两个for循环遍历，直到找到满足要求的答案。主要因题目假设只有一组满足结果的答案，因此难度大大降低，作为第一道题&…...
SSM情侣购物系统-计算机毕业设计源码02387
目 录 摘要 1 绪论 1.1 开发背景与意义 1.2开发意义 1.3Vue.js 主要功能 1.3论文结构与章节安排 2 情侣购物系统系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据流程 3.3.2 业务流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系统用例分…...
09-Spark架构
相比MapReduce僵化的Map与Reduce分阶段计算，Spark计算框架更有弹性和灵活性，运行性能更佳。 1 Spark的计算阶段 MapReduce一个应用一次只运行一个map和一个reduceSpark可根据应用复杂度，分割成更多的计算阶段（stage）…...
挑战5分钟内基于Springboot+SpringMVC+Mybatis-plus快速构建web后端三层架构
目标 在清晨的代码编辑器上，一场新的挑战即将开始。程序员们肃立于安静的办公室，眼神专注地盯着屏幕，等待着编译器的一声提示。 随着编译器输出的激动人心的"start!"的提示，战斗的序幕拉开了。Bug如潮水般涌来&#x…...
浅谈JavaScript中的作用域
前言 今天就来简单聊聊JavaScript中的作用域吧！！！ 正文 我们都知道，在任何一门编程语言里面都是有作用域这个概念的，不然岂不乱套了 在js中的作用域一共分为三种，全局域、函数域和块级作用域 全局域 全…...
Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点 🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分…...
python如何对list求和
如何在Python中对多个list的对应元素求和，前提是每个list的长度一样。比如：a[1，2，3]，b[2，3，4]，c[3，4，5]，对a，b，c的对应元素…...
如何解决mfc100u.dll丢失问题，关于mfc100u.dll丢失的多种解决方法
在计算机使用过程中，我们常常会遇到一些错误提示，其中之一就是“计算显示缺失mfc100u.dll”。这个问题可能会影响到我们的正常使用，因此了解它的原因、表现以及解决方法是非常重要的。小编将详细介绍计算显示缺失mfc100u.dll的问题࿰…...
算法day32
第一题 207. 课程表 步骤一： 通过下图的课程数组,首先画出DAG图（有向无环图） 步骤二： 其次我们按照DAG图，来构建该图的拓扑排序，等有效的点都按照规则排完序后，观察是否有剩下的点的入度不为0&…...
【QT】信号与槽
目录 概述 Q_OBJECT 自定义信号 自定义槽 带参数的信号和槽 信号与槽断开 定义槽函数时，使用lambda表达式 概述 所谓的信号槽，要解决的问题，就是响应用户的操作，这是QT与其他GUI开发框架比较不同的地方。其他的GUI开发框…...
【Java】解决Java报错：IllegalArgumentException
文章目录 引言1. 错误详解2. 常见的出错场景2.1 非法的参数值2.2 空值或 null 参数2.3 非法的数组索引 3. 解决方案3.1 参数验证3.2 使用自定义异常3.3 使用Java标准库中的 Objects 类 4. 预防措施4.1 编写防御性代码4.2 使用注解和检查工具4.3 单元测试 结语 引言 在Java编程…...
完美的移动端 UI 风格让客户无可挑剔
完美的移动端 UI 风格让客户无可挑剔...
【React】在 React 组件中，怎么使用useContext
在React中，useContext 是一个Hook，它允许你无需显式地通过组件树的每一层来传递 props，就能将值深入到组件树的任何位置。要使用 useContext，你需要先创建一个 Context 对象，然后使用这个对象提供的 Provider 组件来包裹你的应用中的一部分。然后，任何在这个 Provider 下…...
【数据结构】栈的应用
目录 0 引言 1 栈在括号匹配中的应用 2 栈在表达式求值中的应用 2.1 算数表达式 2.2 中缀表达式转后缀表达式 2.3 后缀表达式求值 3 栈在递归中的应用 3.1 栈在函数调用中的作用 3.2 栈在函数调用中的工作原理 4 总结 0 引言 栈（Stack）是一…...
Opencv基本操作
Opencv基本操作 导入并使用opencv进行图像与视频的基本处理 opencv读取的格式是BGR import cv2 #opencv读取的格式是BGR import numpy import matplotlib.pyplot as plt %matplotlib inline图像读取 通过cv2.imread()来加载指定位置的图像信息。 img cv2.imread(./res/ca…...
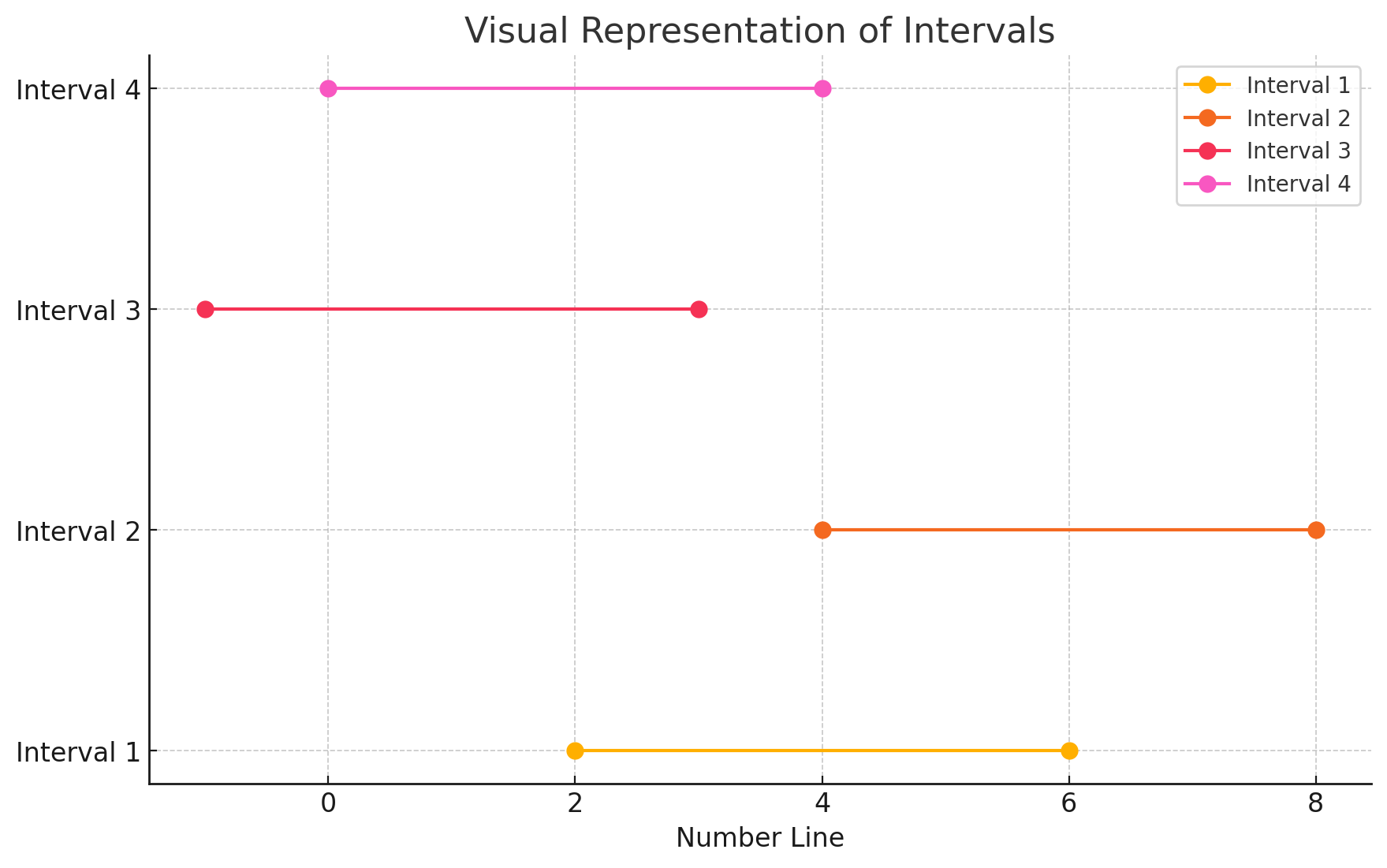
2779. 数组的最大美丽值
简单翻译一下题目意思： 对于每个 nums[i] 都可以被替换成 [nums[i]-k, nums[i]k] 区间中的任何数，区间左右是闭的。在每个数字可以替换的前提下，返回数组中最多的重复数字的数量。 第一想法是用一个哈希表，Key 是可以被替换的数…...
数据库修复实例（航线修复）
修复目标 修复回音群岛 (Echo Isles) 到 赞达拉港 (Port of Zandalar) 的航线 SET TRANSPORT_GUID : 32; SET TRANSPORT_ENTRY : 272677; SET CGUID : 850000;-- Adjust transports DELETE FROM transports WHERE guid TRANSPORT_GUID; INSERT INTO transports (guid, entry…...
视频网站下载利器yt-dlp参数详解
yt-dlp 是一个强大的命令行工具，用来下载 YouTube 和其他网站上的视频和音频。它拥有丰富的参数，可以定制下载行为，满足各种需求。本文将详细介绍 yt-dlp 的参数使用。 一、基本参数 -f, –format FORMAT: 指定下载格式，可以用视…...
别再死磕流程图了！用PAD图搞定详细设计，代码自动生成不是梦
别再死磕流程图了！用PAD图搞定详细设计，代码自动生成不是梦 如果你还在用传统流程图做详细设计，每次修改需求都要重画半张图；如果你受够了N-S图方框套方框的视觉折磨，连个简单循环都要画成俄罗斯套娃——是时候认识PAD…...
STM32F103C8T6 Bootloader分区与跳转详解：手把手配置64KB Flash的16+48分配方案
STM32F103C8T6 Bootloader分区与跳转实战：64KB Flash的1648分配方案深度解析 在嵌入式开发中，Bootloader的设计往往是项目成败的关键一环。对于资源受限的STM32F103C8T6这类仅有64KB Flash的MCU来说，如何在Bootloader和应用程序之间合理分配这…...
告别键盘连击烦恼：KeyboardChatterBlocker 智能解决方案详解
告别键盘连击烦恼：KeyboardChatterBlocker 智能解决方案详解 【免费下载链接】KeyboardChatterBlocker A handy quick tool for blocking mechanical keyboard chatter. 项目地址: https://gitcode.com/gh_mirrors/ke/KeyboardChatterBlocker 你是否曾经在打…...
逆向实战：用WT-JS_DEBUG_V1.8.3快速定位并导出AES加密参数到Python
逆向工程实战：从浏览器到Python的AES加密参数高效迁移指南 在数据采集和接口分析领域，遇到前端加密是再常见不过的挑战。特别是当网站采用AES加密时，如何快速提取关键参数并复用到Python脚本中，成为许多开发者头疼的问题。本文将…...
手把手教你用VSCode+OpenOCD实时查看HPM6750外设寄存器（附SVD文件配置）
手把手教你用VSCodeOpenOCD实时监控HPM6750寄存器状态 调试嵌入式系统时，最令人头疼的莫过于面对一个"黑箱"——明明程序在跑，却看不到硬件寄存器的实时状态。这种盲目操作就像蒙着眼睛修车，效率低下且容易出错。本文将彻底解决这个…...
如何在Windows 11上免费安装安卓子系统：3步快速搭建跨平台应用中心
如何在Windows 11上免费安装安卓子系统：3步快速搭建跨平台应用中心 【免费下载链接】WSA Developer-related issues and feature requests for Windows Subsystem for Android 项目地址: https://gitcode.com/gh_mirrors/ws/WSA 想在Windows电脑上无缝运行手…...
Formation：macOS前端开发环境一键配置终极指南
Formation：macOS前端开发环境一键配置终极指南 【免费下载链接】formation 💻 macOS setup script for front-end development 项目地址: https://gitcode.com/gh_mirrors/fo/formation Formation是一款专为macOS设计的前端开发环境配置脚本&…...
Unity3d之随机生成数字
UnityEngine.Random.Range(min,max)包含最小值不包含最大值Mathf.Clamp是限定范围...
《CVPR2025-DEIM创新改进项目实战：从原理到部署的深度学习优化全攻略》004、DEIM数学基础：注意力机制与特征重标定的统一框架
CVPR2025-DEIM创新改进项目实战：从原理到部署的深度学习优化全攻略 004、DEIM数学基础：注意力机制与特征重标定的统一框架 一、从一次诡异的梯度爆炸说起 去年秋天调一个轻量级检测模型，在T4上跑得好好的，换到Jetson Orin上就炸了——loss直接飞到NaN。查了三天，最后定…...
求职路上的守护与成长
你有没有过这样的时刻——深夜对着海量的招聘信息发呆，投了无数简历却石沉大海，突然觉得前途一片迷茫，特别无助？记得有个学生，为了进心仪的央企准备了半年，却在二面屡屡受挫。那天老师陪他复盘到凌晨&#…...