深入解析数据结构之B树:平衡树中的王者
在计算机科学中,数据结构是算法和程序设计的基础。而在众多数据结构中,B树作为一种平衡树,在数据库和文件系统中有着广泛应用。本文将详细介绍B树的概念、特点、操作、优缺点及其应用场景,帮助读者深入理解这一重要的数据结构。
一、B树简介
B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于实现高效的动态数据存储和检索。B树的设计目的是为了减少磁盘I/O操作次数,从而提高性能。B树的每个节点可以有多个子节点,这使得B树在高度和宽度上更为平衡。
二、B树的特点
1. 节点特性
- 每个节点包含若干个关键字(keys)和指向子节点的指针。
- 关键字按照从小到大的顺序存储,并满足特定的排序规则。
2. 平衡特性
- B树是平衡树,其所有叶子节点在同一层次。
- 每个节点的子节点数在一定范围内(定义为度数或阶数)。
3. 高效性
- B树的高度较低,搜索、插入和删除操作的时间复杂度为O(log n)。
- B树能够有效减少磁盘I/O操作,适合大规模数据存储和管理。
三、B树的操作
1. 搜索
搜索操作在B树中非常高效。由于B树的每个节点包含多个关键字,搜索过程中可以在节点内部进行二分查找,从而快速定位目标关键字或子节点。
搜索操作伪代码:
def search_btree(node, key):i = 0while i < len(node.keys) and key > node.keys[i]:i += 1if i < len(node.keys) and key == node.keys[i]:return node # 找到关键字elif node.is_leaf:return None # 未找到关键字else:return search_btree(node.children[i], key) # 递归搜索子节点2. 插入
插入操作需要保持B树的平衡性。当节点已满时,需要进行节点分裂(split),将节点分为两个,并将中间关键字提升到父节点。
插入操作步骤:
- 找到插入位置。
- 插入关键字。
- 如果节点满了,进行分裂。
3. 删除
删除操作较为复杂,需要处理多个情况。删除关键字后,需要保持B树的平衡性。如果节点关键字数量少于最小值,需要进行节点合并或借用兄弟节点的关键字。
删除操作步骤:
- 找到删除位置。
- 删除关键字。
- 处理节点合并或关键字借用,保持树的平衡性。
四、B树的优缺点
优点
- 高效性:B树的高度较低,操作复杂度为O(log n),适合大规模数据存储和检索。
- 磁盘友好:B树设计初衷是减少磁盘I/O操作,提高存取速度。
- 平衡性:B树保持了较好的平衡性,所有叶子节点在同一层次。
缺点
- 实现复杂:B树的插入和删除操作较为复杂,需要处理多种情况。
- 空间利用率较低:为了保持平衡性,B树节点可能需要预留较多空闲空间,导致空间利用率较低。
五、B树的应用场景
1. 数据库索引
B树广泛应用于数据库系统中,作为索引结构。其高效的搜索、插入和删除操作,使得B树成为数据库索引的首选数据结构。
2. 文件系统
文件系统中,B树用于实现目录和文件的快速查找。B树的平衡性和高效性,使其能够有效管理大规模文件和目录结构。
3. 内存管理
在内存管理中,B树用于快速分配和回收内存块。B树的高效搜索和删除操作,使其能够快速定位和管理内存块。
六、B树的具体实现(Java代码示例)
下面是B树的Java实现,包括插入和搜索操作的示例代码:
// B树节点类
class BTreeNode {int[] keys; // 节点中存储的关键字数组int degree; // B树的度数BTreeNode[] children; // 子节点数组int numKeys; // 当前节点中的关键字数量boolean isLeaf; // 是否为叶子节点// 构造函数public BTreeNode(int degree, boolean isLeaf) {this.degree = degree;this.isLeaf = isLeaf;this.keys = new int[2 * degree - 1];this.children = new BTreeNode[2 * degree];this.numKeys = 0;}// 插入和分裂等方法在此定义
}// B树类
class BTree {private BTreeNode root; // 根节点private int degree; // B树的度数// 构造函数public BTree(int degree) {this.root = null;this.degree = degree;}// 插入关键字public void insert(int key) {if (root == null) {// 如果根节点为空,则创建一个新的根节点root = new BTreeNode(degree, true);root.keys[0] = key;root.numKeys = 1;} else {if (root.numKeys == 2 * degree - 1) {// 如果根节点已满,则需要分裂BTreeNode newNode = new BTreeNode(degree, false);newNode.children[0] = root;splitChild(newNode, 0, root);int i = 0;if (newNode.keys[0] < key) {i++;}insertNonFull(newNode.children[i], key);root = newNode;} else {insertNonFull(root, key);}}}// 分裂子节点private void splitChild(BTreeNode parentNode, int i, BTreeNode fullNode) {BTreeNode newNode = new BTreeNode(fullNode.degree, fullNode.isLeaf);newNode.numKeys = degree - 1;for (int j = 0; j < degree - 1; j++) {newNode.keys[j] = fullNode.keys[j + degree];}if (!fullNode.isLeaf) {for (int j = 0; j < degree; j++) {newNode.children[j] = fullNode.children[j + degree];}}fullNode.numKeys = degree - 1;for (int j = parentNode.numKeys; j >= i + 1; j--) {parentNode.children[j + 1] = parentNode.children[j];}parentNode.children[i + 1] = newNode;for (int j = parentNode.numKeys - 1; j >= i; j--) {parentNode.keys[j + 1] = parentNode.keys[j];}parentNode.keys[i] = fullNode.keys[degree - 1];parentNode.numKeys++;}// 插入非满节点private void insertNonFull(BTreeNode node, int key) {int i = node.numKeys - 1;if (node.isLeaf) {while (i >= 0 && node.keys[i] > key) {node.keys[i + 1] = node.keys[i];i--;}node.keys[i + 1] = key;node.numKeys++;} else {while (i >= 0 && node.keys[i] > key) {i--;}if (node.children[i + 1].numKeys == 2 * degree - 1) {splitChild(node, i + 1, node.children[i + 1]);if (node.keys[i + 1] < key) {i++;}}insertNonFull(node.children[i + 1], key);}}// 遍历B树public void traverse() {if (root != null) {traverse(root);}}private void traverse(BTreeNode node) {int i;for (i = 0; i < node.numKeys; i++) {if (!node.isLeaf) {traverse(node.children[i]);}System.out.print(" " + node.keys[i]);}if (!node.isLeaf) {traverse(node.children[i]);}}// 搜索关键字public boolean search(int key) {return root != null && search(root, key) != null;}private BTreeNode search(BTreeNode node, int key) {int i = 0;while (i < node.numKeys && key > node.keys[i]) {i++;}if (i < node.numKeys && key == node.keys[i]) {return node;}return node.isLeaf ? null : search(node.children[i], key);}
}// 测试类
public class Main {public static void main(String[] args) {BTree btree = new BTree(3);btree.insert(10);btree.insert(20);btree.insert(5);btree.insert(6);btree.insert(12);btree.insert(30);btree.insert(7);btree.insert(17);System.out.println("Traversal of the constructed B-tree:");btree.traverse();int key = 6;if (btree.search(key)) {System.out.println("\nKey " + key + " is present in the B-tree.");} else {System.out.println("\nKey " + key + " is not present in the B-tree.");}}
}七、总结
B树作为一种平衡树数据结构,在数据库和文件系统中有着广泛的应用。它通过高效的搜索、插入和删除操作,实现了大规模数据的快速存储和检索。尽管B树的实现较为复杂,但其在实际应用中的高效性和可靠性使其成为数据结构领域的重要组成部分。通过本文的介绍,相信读者能够深入理解B树的原理、特点和应用场景,并掌握其基本操作和实现方法。
感谢您阅读本文,欢迎“一键三连”。作者定会不负众望,按时按量创作出更优质的内容。
❤️ 1. 毕业设计专栏,毕业季咱们不慌,上千款毕业设计等你来选。
相关文章:

深入解析数据结构之B树:平衡树中的王者
在计算机科学中,数据结构是算法和程序设计的基础。而在众多数据结构中,B树作为一种平衡树,在数据库和文件系统中有着广泛应用。本文将详细介绍B树的概念、特点、操作、优缺点及其应用场景,帮助读者深入理解这一重要的数据结构。 …...
18. 第十八章 继承
18. 继承 和面向对象编程最常相关的语言特性就是继承(inheritance). 继承值得是根据一个现有的类型, 定义一个修改版本的新类的能力. 本章中我会使用几个类来表达扑克牌, 牌组以及扑克牌性, 用于展示继承特性.如果你不玩扑克, 可以在http://wikipedia.org/wiki/Poker里阅读相关…...
)
OperationalError: (_mysql_exceptions.OperationalError)
OperationalError: (_mysql_exceptions.OperationalError) (2006, MySQL server has gone away) 这个错误通常表示客户端(例如你的 Python 程序使用 SQLAlchemy 连接到 MySQL 数据库)和 MySQL 服务器之间的连接被异常关闭了。这个问题可能由多种原因引起,以下是一些常见的原…...

DocGraph相关概念
结合简化版的直观性和专业版的深度,我们可以得到一个既易于理解又包含专业细节的DocGraph概念讲解。 DocGraph概述(简化版) 想象DocGraph就像是文章信息的地图。它通过拆分文档、识别关键词、分析关系,并最终以图形方式呈现这些…...
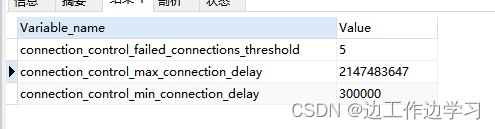
MySQL限制登陆失败次数配置
目录 一、限制登陆策略 1、Windows 2、Linux 一、限制登陆策略 1、Windows 1)安装插件 登录MySQL数据库 mysql -u root -p 执行命令安装插件 #限制登陆失败次数插件 install plugin CONNECTION_CONTROL soname connection_control.dll;install plugin CO…...

洛谷题解 - P1192 台阶问题
目录 题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示代码 题目描述 有 N N N 级台阶,你一开始在底部,每次可以向上迈 1 ∼ K 1\sim K 1∼K 级台阶,问到达第 N N N 级台阶有多少种不同方式。 输入格式 两个正整数 N , K …...
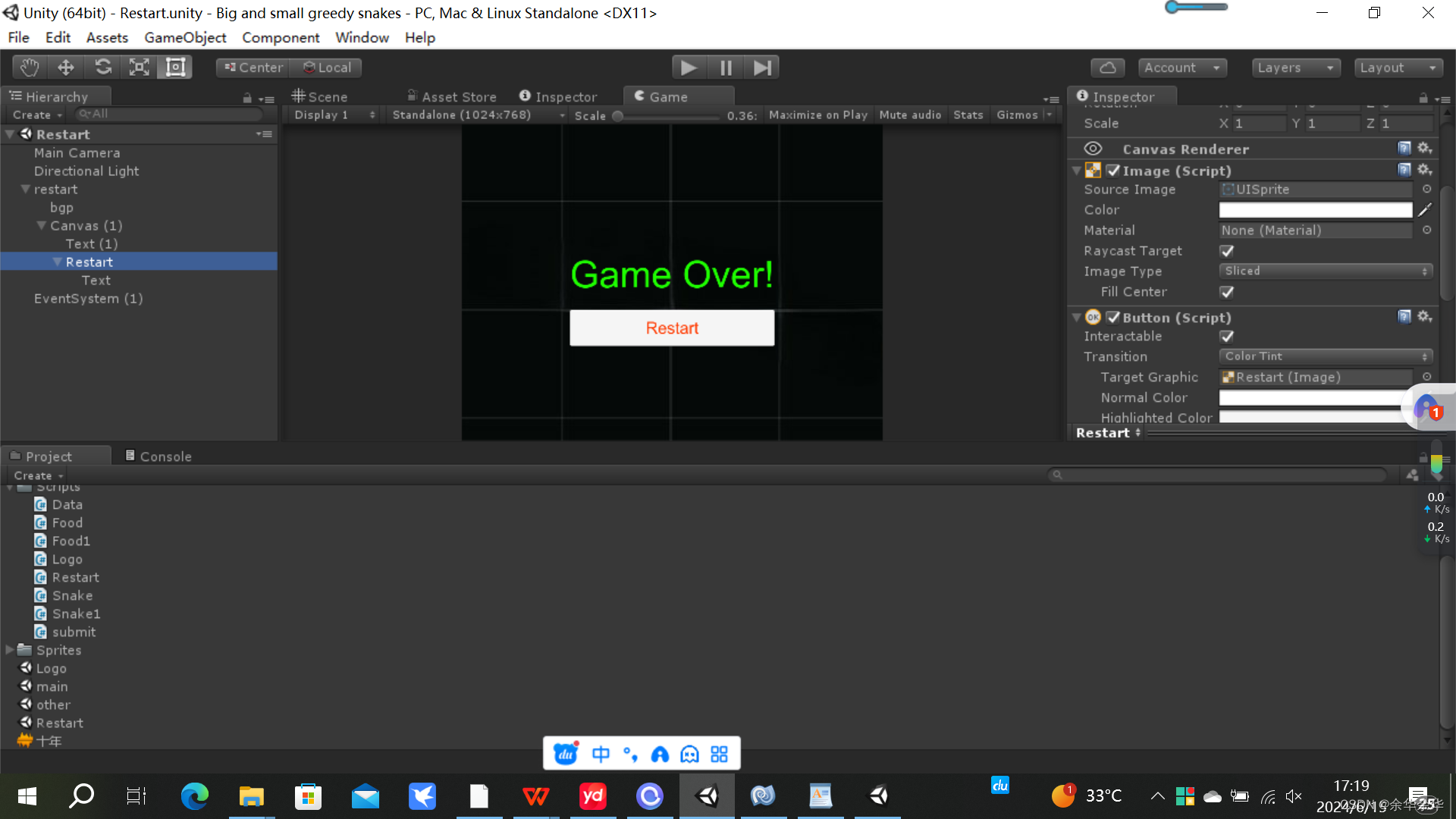
Unity贪吃蛇改编【详细版】
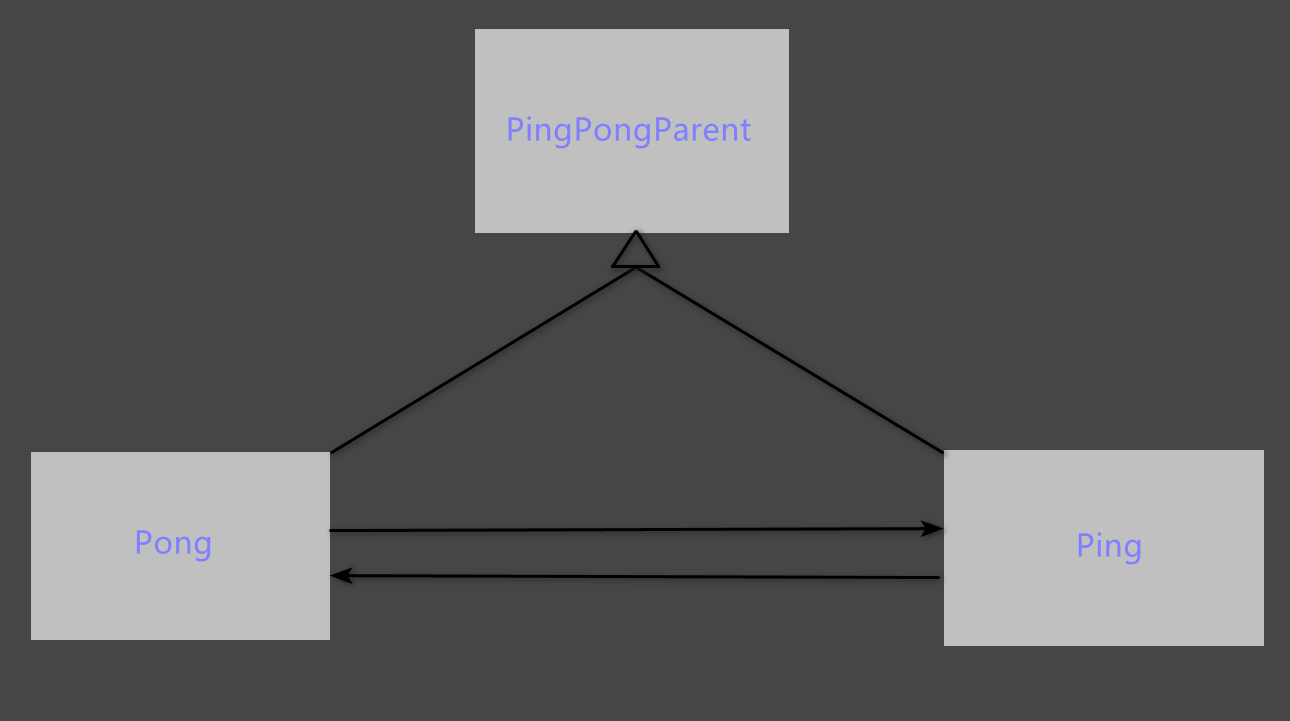
Big and small greedy snakes 游戏概述 游戏亮点 通过对称的美感,设置两条贪吃蛇吧,其中一条加倍成长以及加倍减少,另一条正常成长以及减少,最终实现两条蛇对整个界面的霸占效果。 过程中不断记录两条蛇的得分情况,…...

React中数据响应式原理
React作为当下最流行的前端框架之一,以其声明式编程和组件化架构而广受开发者喜爱。而React的数据响应式原理,是其高效更新DOM的核心机制。本文将深入探讨React中数据响应式原理,并结合代码示例进行论证。 响应式原理概述 在React中&#x…...
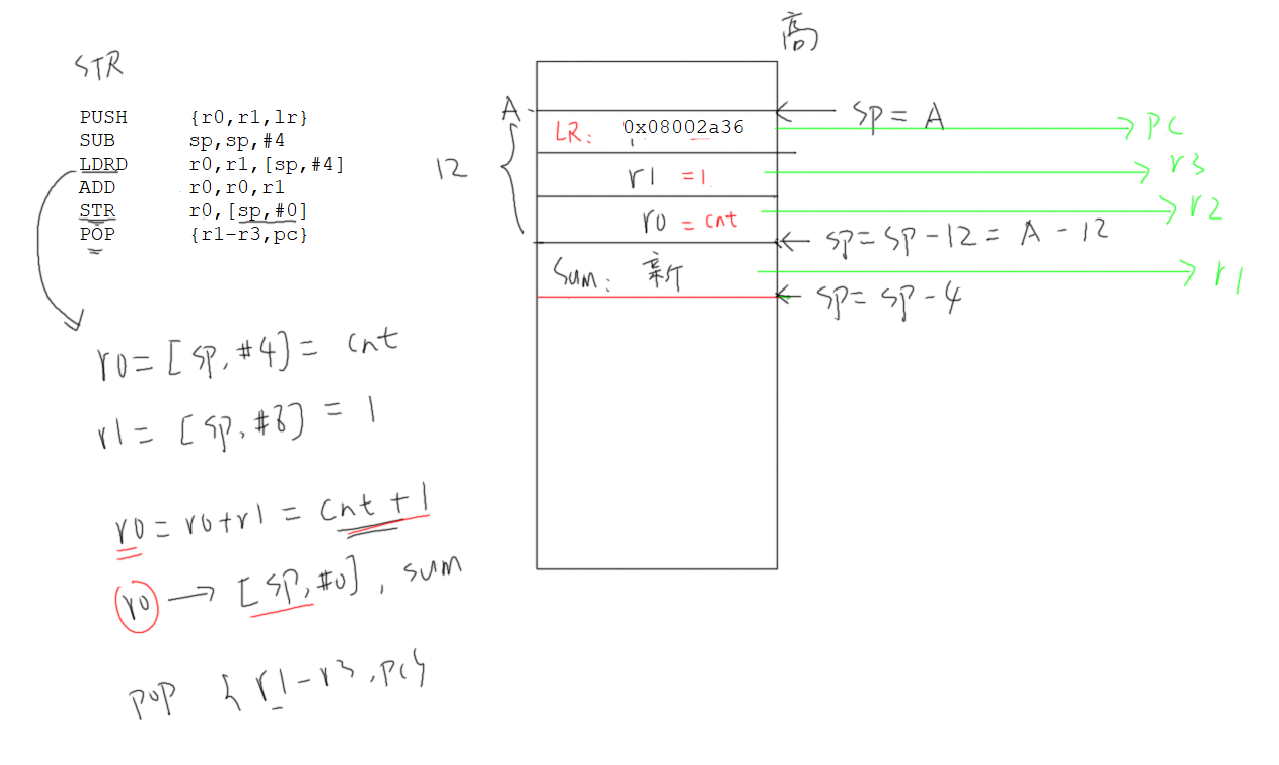
【FreeRTOS】ARM架构汇编实例
目录 ARM架构简明教程1. ARM架构电脑的组成1.2 RISC1.2 提出问题1.3 CPU内部寄存器1.4 汇编指令 2. C函数的反汇编 学习视频 【FreeRTOS入门与工程实践 --由浅入深带你学习FreeRTOS(FreeRTOS教程 基于STM32,以实际项目为导向)】 https://www.…...

【Linux】常见指令的使用
文章目录 which指令stat 指令wc指令echo指令tree 指令whoami指令clear指令alias指令ls指令pwd指令cd 指令touch指令mkdir指令(重要)rmdir指令 && rm 指令(重要)man指令(重要)cp指令(重要…...

C#面:详细阐述什么是 DTO
DTO(Data Transfer Object)是一种设计模式,用于在不同层之间传输数据。它的主要目的是在应用程序的不同部分之间传递数据,而不是直接传递实体对象。DTO通常是一个简单的POCO(Plain Old CLR Object)…...
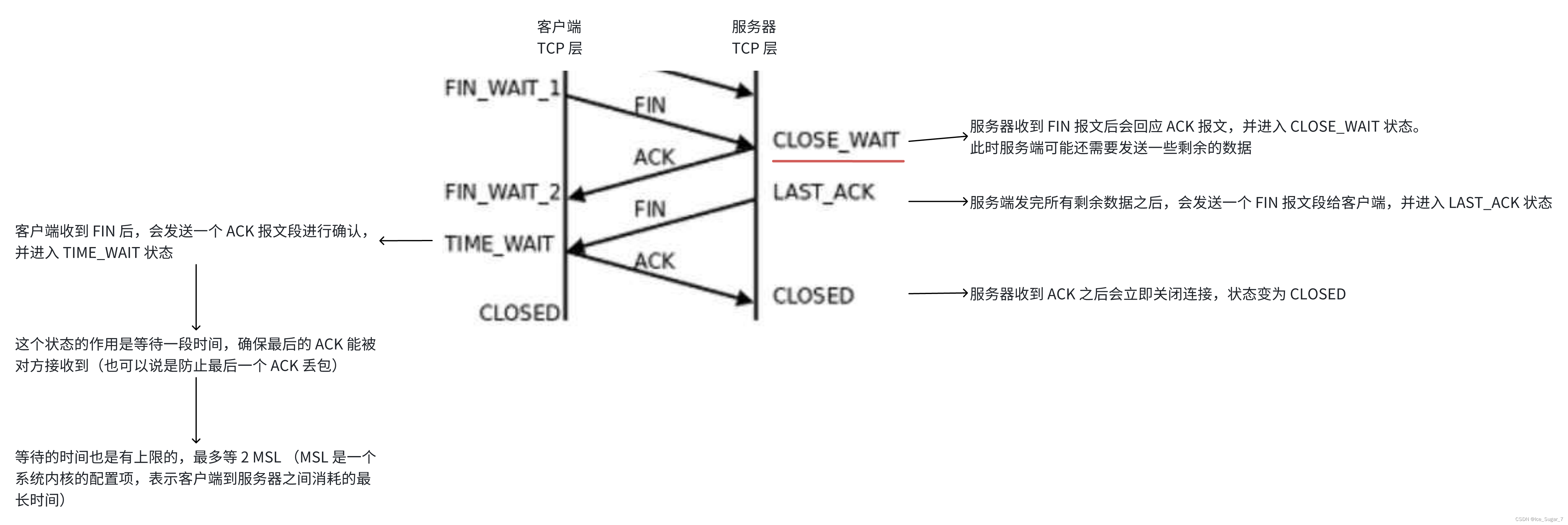
「TCP 重要机制」三次握手四次挥手
🎇个人主页:Ice_Sugar_7 🎇所属专栏:计网 🎇欢迎点赞收藏加关注哦! 三次握手&四次挥手 🍉连接管理🍌三次握手🍌意义🍌四次挥手🍌TCP 状态转换…...

Java数据库编程
引言 在现代应用开发中,与数据库交互是不可或缺的一部分。Java提供了JDBC(Java Database Connectivity) API,允许开发者方便地连接到数据库并执行SQL操作。本文将详细介绍Java数据库编程的基础知识,包括JDBC的基本概念…...

决策树算法介绍:原理与案例实现
一、引言 决策树是一种常用于分类和回归任务的机器学习算法,因其易于理解和解释的特点,在数据分析和挖掘领域有着广泛应用。本文将介绍决策树算法的基本原理,并通过一个具体案例展示如何实现和应用该算法。 二、决策树算法原理 1. 决策树结…...

业务代表模式
业务代表模式 引言 在软件工程中,设计模式是解决常见问题的经典解决方案。它们为开发人员提供了一种方法,以优雅和可重用的方式处理软件开发中的挑战。业务代表模式(Business Delegate Pattern)是一种行为设计模式,它主要关注于将业务逻辑与表示层(如用户界面)分离,以…...

LeetCode 算法:反转链表 c++
原题链接🔗:反转链表 难度:简单⭐️ 题目 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2:…...
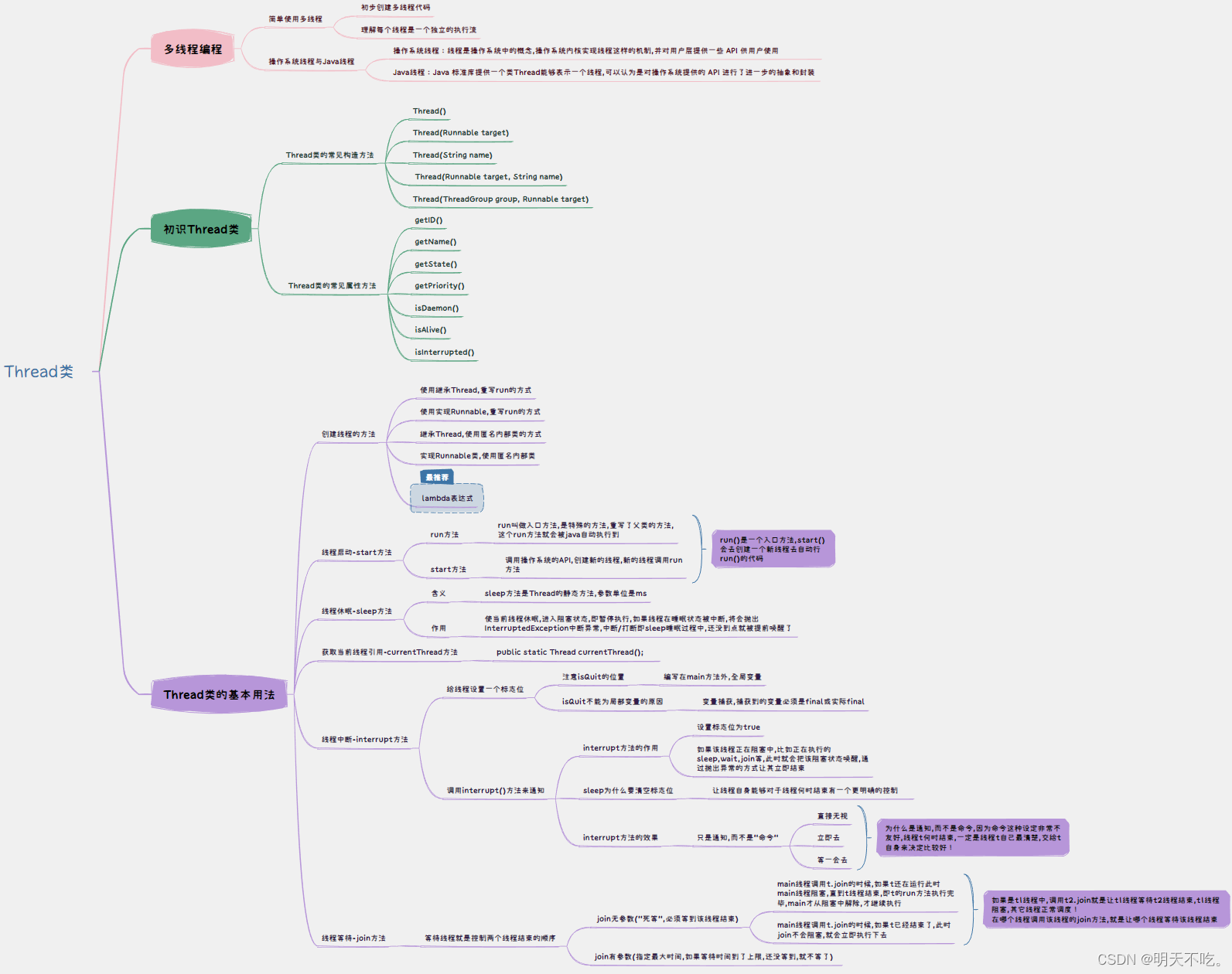
【多线程】Thread类及其基本用法
🥰🥰🥰来都来了,不妨点个关注叭! 👉博客主页:欢迎各位大佬!👈 文章目录 1. Java中多线程编程1.1 操作系统线程与Java线程1.2 简单使用多线程1.2.1 初步创建新线程代码1.2.2 理解每个…...

Springboot 整合 Flowable(一):使用 flowable-UI 绘制流程图
目录 一、Flowable简介 二、Flowable 与 Activiti 的区别 三、流程图的绘制(以员工请假流程图为例) 1、下载 flowable 的压缩包: 2、启动包中的 tomcat 3、登录页面 4、绘制结束,导出 bpmn20.xml文件 一、Flowable简介 Fl…...

课设--学生成绩管理系统(一)
欢迎来到 Papicatch的博客 文章目录 🍉技术核心 🍉引言 🍈标识 🍈背景 🍈项目概述 🍈 文档概述 🍉可行性分析的前提 🍈项目的要求 🍈项目的目标 🍈…...

thinkphp5模型的高级应用
ThinkPHP5 是一个基于 PHP 的轻量级框架,它提供了许多便利的功能来简化 Web 开发。在 ThinkPHP5 中,模型(Model)是 MVC(Model-View-Controller)架构中的重要组成部分,负责处理数据逻辑。以下是一…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
