【二】【动态规划NEW】91. 解码方法,62. 不同路径,63. 不同路径 II
91. 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,“11106” 可以映射为:
“AAJF” ,将消息分组为 (1 1 10 6)
“KJF” ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 “06” 不能映射为 “F” ,这是由于 “6” 和 “06” 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = “12”
输出:2
解释:它可以解码为 “AB”(1 2)或者 “L”(12)。
示例 2:
输入:s = “226”
输出:3
解释:它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。
示例 3:
输入:s = “06”
输出:0
解释:“06” 无法映射到 “F” ,因为存在前导零(“6” 和 “06” 并不等价)。
提示:
1 <= s.length <= 100
s 只包含数字,并且可能包含前导零。
利用递归思想写动态规划,字符串s返回解码的方法数,f(i)表示0~i区间的解码方法数.
字符串s的长度是n,我们需要得到f(n).
f(i)函数求解0~i区间的解码方法数,
可以让i位置字符单独解码,也可以让i和i-1位置字符两个一起解码.
如果让i位置字符单独解码,此时产生的解码方法数是f(i-1).
如果让i和i-1位置共同解码,此时产生的解码方法数是f(i-2).
如果让i位置字符单独解码需要满足的条件是s[i]!=‘0’.
如果让i和i-1位置字符共同解码需要满足的条件是s[i-1]!=‘0’,并且i-1和i位置字符属于1~26.
根据递归思想直接写动态规划写法.
状态表示,定义dp[i]表示0~i区间的解码方法数.
状态转移方程,如果让i位置字符单独解码,此时产生的解码方法数是dp[i-1].
如果让i和i-1位置共同解码,此时产生的解码方法数是dp[i-2].
填表顺序,填写i位置状态需要用到i-1,i-2位置状态,i需要从小到大.
初始化,特判,最开始的可以直接得出答案的就手动填写,越界的用三目表达式解决.
#define debug // 定义 debug 宏
#ifdef debug // 如果定义了 debug
#define bug(code) do{cout<<"L"<<__LINE__<<":"<<endl;code;}while(0) // 定义 bug 宏,输出当前行号并执行代码块
#else
#define bug(code) do{}while(0) // 如果没有定义 debug,bug 宏为空操作
#endifclass Solution {
public:int ret; // 用于存储结果的整数string s; // 输入字符串vector<int>dp; // 动态规划数组void solve(){ // 解决问题的函数ret=0; // 初始化结果为 0dp.assign(s.size(),-1); // 将动态规划数组初始化为 -1,大小为输入字符串的长度dp[0]=1; // 初始条件,dp[0] 设为 1for(int i=1;i<dp.size();i++){ // 从第 1 个字符开始遍历字符串int ans=0; // 用于存储当前字符的解码方法数if(s[i]!='0') ans+=dp[i-1]; // 如果当前字符不是 '0',则可以单独解码,加上 dp[i-1]if(s[i-1]!='0'&&(s[i-1]-'0')*10+(s[i]-'0')<=26) ans+=(i-2>=0?dp[i-2]:1); // 如果前一个字符不是 '0',且当前和前一个字符组成的数字小于等于 26,则可以合并解码,加上 dp[i-2](如果 i-2 小于 0,则加 1)dp[i]=ans; // 更新 dp[i] 为当前的解码方法数}ret=dp[dp.size()-1]; // 最后的结果是 dp 数组的最后一个值bug( // 如果定义了 debug,输出 dp 数组for(int i=0;i<dp.size();i++){ // 遍历 dp 数组cout<<dp[i]<<" "; // 输出 dp 数组的每一个值}cout<<endl; // 换行);}int numDecodings(string _s) { // 主函数,接收输入字符串ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 加速输入输出s=_s; // 将输入字符串赋值给成员变量 sif(s[0]=='0') return 0; // 如果字符串以 '0' 开头,返回 0solve(); // 调用 solve 函数求解return ret; // 返回结果}
};62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
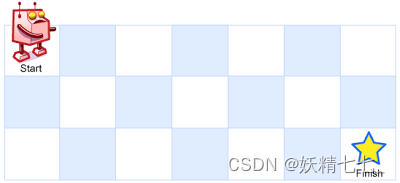
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
f(i,j)表示从(0,0)位置到达(i,j)位置的路径数,我们需要的返回值是f(row,col).
f(i,j)=f(i-1,j)+f(i,j-1).
递归出口,如果是(0,0)位置,返回1.
如果越界了返回0.
利用递归思想直接写动态规划,定义状态标识dp[i][j]表示(0,0)位置到达(i,j)位置的路径数,需要的返回值是dp[row][col].
状态转移方程,dp[i][j]=dp[i-1][j]+dp[i][j-1].
初始化,特判,越界情况用三目表达式解决.
填表顺序,i需要从小到大填写.
#define debug // 定义 debug 宏
#ifdef debug // 如果定义了 debug
#define bug(code) do{cout<<"L"<<__LINE__<<":"<<endl;code;}while(0) // 定义 bug 宏,输出当前行号并执行代码块
#else
#define bug(code) do{}while(0) // 如果没有定义 debug,bug 宏为空操作
#endif
class Solution {
public:int row, col; // 定义行数和列数int ret; // 用于存储结果的整数vector<vector<int>> dp; // 动态规划数组void solve() { // 解决问题的函数ret = 0; // 初始化结果为 0dp.assign(row + 1, vector<int>(col + 1, -1)); // 初始化 dp 数组为 -1,大小为 (row+1) x (col+1)for (int i = 1; i <= row; i++) { // 遍历每一行for (int j = 1; j <= col; j++) { // 遍历每一列if (i == 1 && j == 1) { // 如果是起点位置 (1, 1)dp[i][j] = 1; // 起点位置的路径数为 1continue; // 跳过后续计算}dp[i][j] = (i - 1 >= 1 ? dp[i - 1][j] : 0) + (j - 1 >= 1 ? dp[i][j - 1] : 0); // 计算当前位置的路径数}}ret = dp[row][col]; // 最后的结果是 dp 数组的右下角值bug( // 如果定义了 debug,输出 dp 数组for (int i = 1; i <= row; i++) { // 遍历 dp 数组的每一行for (int j = 1; j <= col; j++) { // 遍历 dp 数组的每一列cout << dp[i][j] << " "; // 输出 dp 数组的每一个值}cout << endl; // 换行}cout << endl; // 换行);}int uniquePaths(int _m, int _n) { // 主函数,接收输入的行数和列数ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出col = _n, row = _m; // 将输入的行数和列数赋值给成员变量solve(); // 调用 solve 函数求解return ret; // 返回结果}
};63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
网格里面有障碍物,填表的时候,障碍物的位置是不需要填写的,并且为了不影响其他位置的填写,如果是障碍物dp值设置为0即可,如果不设置为0,在状态转移方程哪里就需要多判断一下.
用三目运算符解决越界的情况.
#define debug // 定义 debug 宏
#ifdef debug // 如果定义了 debug
#define bug(code) do{cout<<"L"<<__LINE__<<":"<<endl;code;}while(0) // 定义 bug 宏,输出当前行号并执行代码块
#else
#define bug(code) do{}while(0) // 如果没有定义 debug,bug 宏为空操作
#endif
class Solution {
public:vector<vector<int>> arr; // 存储输入的障碍物网格int ret; // 用于存储结果的整数vector<vector<int>> dp; // 动态规划数组void solve() { // 解决问题的函数dp.assign(arr.size(), vector<int>(arr[0].size(), -1)); // 初始化 dp 数组为 -1,大小与输入网格相同for (int i = 0; i < arr.size(); i++) { // 遍历每一行for (int j = 0; j < arr[0].size(); j++) { // 遍历每一列if (arr[i][j] == 1) dp[i][j] = 0; // 如果当前位置是障碍物,路径数为 0if (arr[i][j] == 1) continue; // 如果当前位置是障碍物,跳过后续计算if (i == 0 && j == 0) { dp[i][j] = 1; continue; } // 起点位置的路径数为 1dp[i][j] = (i - 1 >= 0 ? dp[i - 1][j] : 0) + (j - 1 >= 0 ? dp[i][j - 1] : 0); // 计算当前位置的路径数}}ret = dp[arr.size() - 1][arr[0].size() - 1]; // 最后的结果是 dp 数组的右下角值}int uniquePathsWithObstacles(vector<vector<int>>& _obstacleGrid) { // 主函数,接收输入的障碍物网格ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出arr = _obstacleGrid; // 将输入的障碍物网格赋值给成员变量solve(); // 调用 solve 函数求解return ret; // 返回结果}
};结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【二】【动态规划NEW】91. 解码方法,62. 不同路径,63. 不同路径 II
91. 解码方法 一条包含字母 A-Z 的消息通过以下映射进行了 编码 : ‘A’ -> “1” ‘B’ -> “2” … ‘Z’ -> “26” 要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法ÿ…...

Python闯LeetCode--第3题:无重复字符的最长子串
Problem: 3. 无重复字符的最长子串 文章目录 思路解题方法复杂度Code 思路 一上来马上想到两层for循环暴力枚举,但是又立马想到复杂度是 O ( n 2 ) O(n^2) O(n2),思考了一下能否有更优解,于是想到用头尾两个指针来指定滑动窗口(主…...

HTML DOM 对象
HTML DOM 对象 1. 概述 HTML DOM(文档对象模型)是一个跨平台和语言独立的接口,它允许程序和脚本动态地访问和更新文档的内容、结构和样式。在HTML DOM中,文档被表示为节点树,其中每个节点代表文档中的一个部分,例如元素、文本或属性。HTML DOM对象是构成这个节点树的基…...

如何解决 BeautifulSoup 安装问题:从 BeautifulSoup 3 到 BeautifulSoup 4
在使用 Python 的过程中,解析 HTML 和 XML 数据是一项常见任务。BeautifulSoup 是一个非常流行的解析库。然而,最近在安装 BeautifulSoup 时,遇到了一些问题。本文将介绍如何解决这些问题,并成功安装 BeautifulSoup 4。 问题描述 …...

原型模式--深复制/浅复制
原型模式用于克隆复杂对象,由于new一个实例对象会消耗大部分时间,所以原型模式可以节约大量时间 1 public class Sheep implements Cloneable{2 private String name;3 private Date birth;4 public Sheep(String name, Date birth) {5 …...
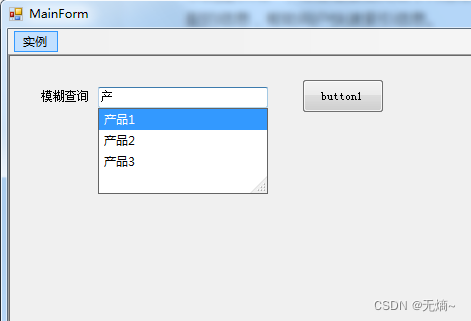
C# TextBox模糊查询及输入提示
在程序中,我们经常会遇到文本框中不知道输入什么内容,这时我们可以在文本框中显示提示词提示用户;或者需要查询某个内容却记不清完整信息,通常可以通过文本框列出与输入词相匹配的信息,帮助用户快速索引信息。 文本框…...
Node入门以及express创建项目
前言 记录学习NodeJS 一、NodeJS是什么? Node.js 是一个开源和跨平台的 JavaScript 运行时环境 二、下载NodeJs 1.下载地址(一直点击next即可,记得修改安装地址) https://nodejs.p2hp.com/download/ 2.查看是否安装成功,打开命令行 nod…...
Cheat Engine CE v7.5 安装教程(专注于游戏的修改器)
前言 Cheat Engine是一款专注于游戏的修改器。它可以用来扫描游戏中的内存,并允许修改它们。它还附带了调试器、反汇编器、汇编器、变速器、作弊器生成、Direct3D操作工具、系统检查工具等。 一、下载地址 下载链接:http://dygod/source 点击搜索&…...
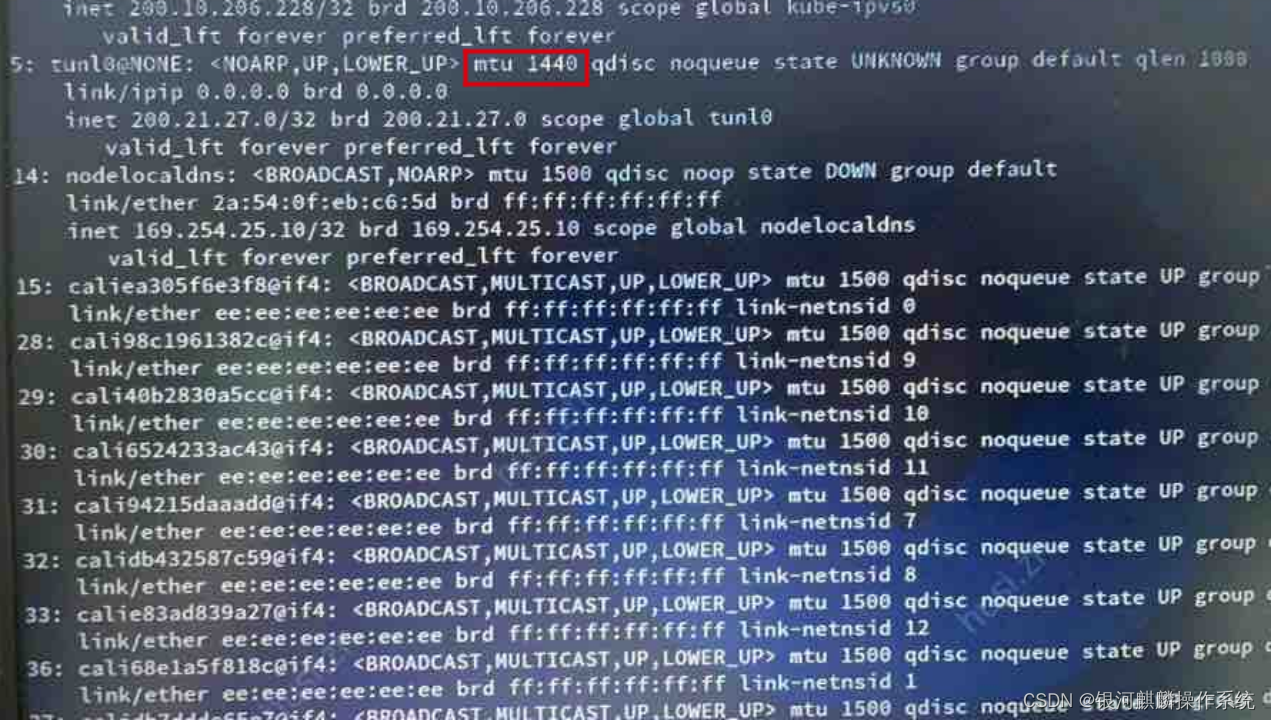
【实例分享】访问后端服务超时,银河麒麟服务器操作系统分析及处理建议
1.服务器环境以及配置 【机型】 处理器: Intel 32核 内存: 128G 整机类型/架构: x86_64虚拟机 【内核版本】 4.19.90-25.22.v2101.kylin.x86_64 【OS镜像版本】 kylin server V10 SP2 【第三方软件】 开阳k8s 2.问题现象描述 …...

Java中和的区别
在Java中,& 和 && 都是逻辑运算符,但它们之间存在一些重要的区别,特别是在它们如何评估其操作数以及它们的性能影响方面。 短路评估(Short-Circuit Evaluation): &&(逻辑…...
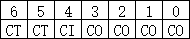
深入理解计算机系统 CSAPP 家庭作业6.34
第一步先求(S,E,B,m) 题目说共C32个字节,块大小B为16个字节,那就是分为两组:0,1.然后每组存4个int 每个4字节 CB*E*S .B16 ,直接映射的E就是1,所以S2 m为啥等于7? 通过写出两个数组所有的地址可以得出m7. 得出高速缓存的参数:(S,E,B,m)(2,1,16,7),注意图6-26每个参数的定义…...

[leetcode 141环形链表]双指针解决环形链表
Problem: 141. 环形链表 文章目录 思路Code 思路 首先想到如果链表为空直接返回false 其次想到用双指针,一个一回走一步,另一个一回走两步 如果是环形,总有一个时刻,两指针会指向同一个节点,而且该结点不能为空(空是快指针遍历完单链表了) Code /*** Definition for singly-li…...

【深度学习】Precision、Accuracy的区别,精确率与准确率:深度学习多分类问题中的性能评估详解
在深度学习的多分类问题中,Precision(精确率)和Accuracy(准确率)是两种常用的性能评估指标,它们各自有不同的定义和用途。 Precision(精确率)的中文发音是:pǔ rēi xī…...
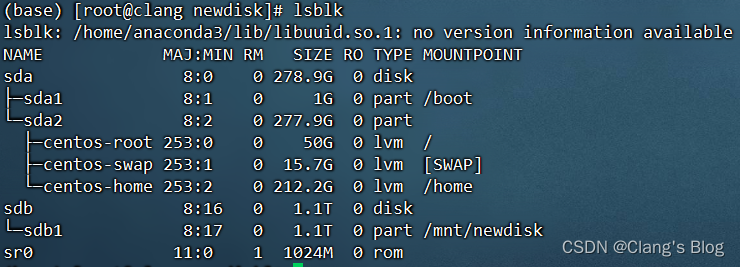
DELL服务器插入新磁盘、创建虚拟磁盘、挂载磁盘步骤
文章目录 一、磁盘清理(可选,针对新硬盘是Foreign状态)1、进入VD Mgmt2、清理新硬盘配置 二、创建虚拟磁盘1、进入Device Settings2、创建虚拟磁盘 三、挂载磁盘到系统1、分区磁盘(注意实际磁盘的名称)2、格式化分区3、…...

springboot与flowable(10):网关服务(排他网关)
一、绘制流程图 排他网关用于对流程中的决策建模。当执行到这个网关时,会按照所有出口顺序流定义的顺序对它们进行计算。选择第一个条件为true的顺序流继续流程。例如员工请假时,小于等于3天由组长审批,大于3天由总监审批。流程案例ÿ…...

Web前端网页源代码:深入剖析与实用技巧
Web前端网页源代码:深入剖析与实用技巧 在Web开发的浩瀚领域中,前端网页源代码扮演着至关重要的角色。它不仅是网页的骨架,更是实现各种交互和视觉效果的基石。本文将从四个方面、五个方面、六个方面和七个方面,对Web前端网页源代…...

聊天页面样式
聊天页面样式 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><link rel"styleshee…...

PHP入门教程3:数组和字符串操作
PHP入门教程3:数组和字符串操作 在前两篇文章中,我们学习了PHP的基础语法、控制结构和函数的使用。本文将重点介绍数组和字符串的高级操作,这些是PHP编程中非常常见且重要的内容。本文将包含以下几个部分: 数组的类型和操作多维…...

mariadb
MariaDB安装配置、使用、授权、增删改查以及数据库备份与恢复 MariaDB安装配置、使用、授权、增删改查以及数据库备份与恢复_mariadb安装及配置教程-CSDN博客mariadb 恢复: ERROR! MySQL server PID file could not be found! 170104 23:04:21 InnoDB: The InnoD…...
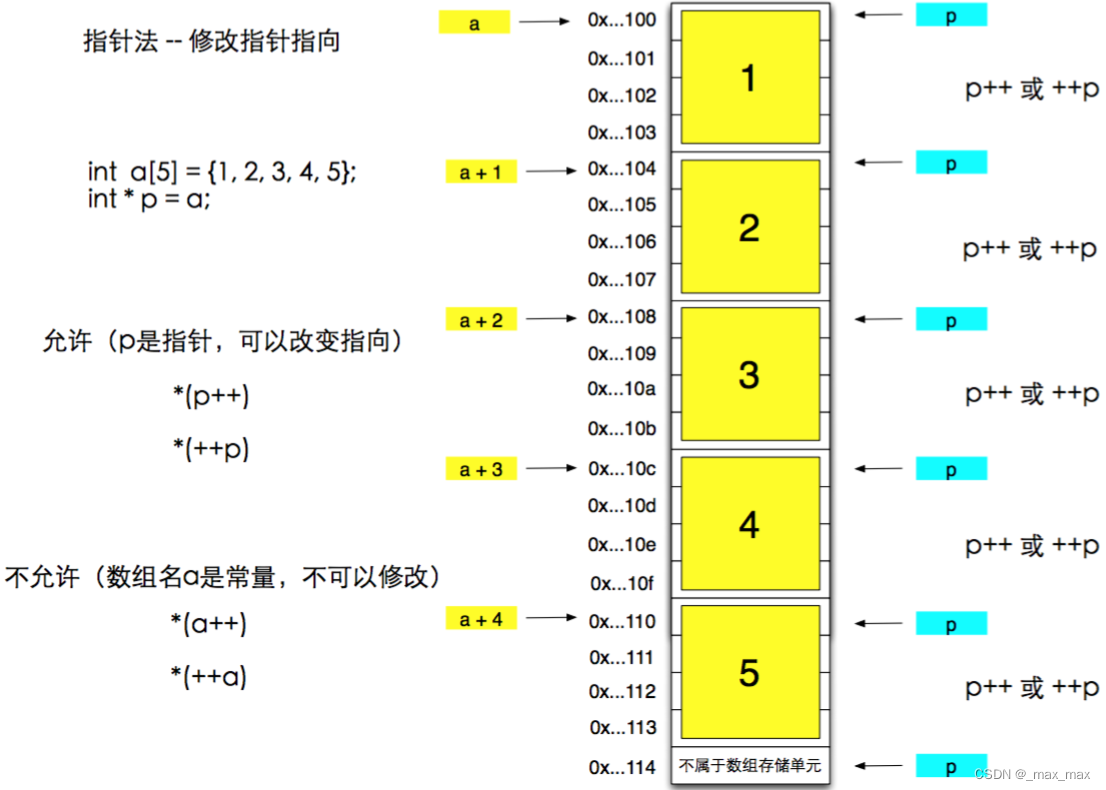
C/C++:指针用法详解
C/C:指针 指针概念 指针变量也是一个变量 指针存放的内容是一个地址,该地址指向一块内存空间 指针是一种数据类型 指针变量定义 内存最小单位:BYTE字节(比特) 对于内存,每个BYTE都有一个唯一不同的编号…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
