一文彻底理解机器学习 ROC-AUC 指标
在机器学习和数据科学的江湖中,评估模型的好坏是非常关键的一环。而 ROC(Receiver Operating Characteristic)曲线和 AUC(Area Under Curve)正是评估分类模型性能的重要工具。
这个知识点在面试中也很频繁的出现。尽管理解这些概念本身不难,但许多人在复习时容易混淆,或在面试紧张时忘记,影响回答效果。
本篇文章将会从基础概念入手,逐步深入到实际操作。我们会详细解释 ROC 曲线和 AUC 的定义和意义,通过实例和代码示范帮助大侠掌握这些工具的使用方法,最后通过一些实际应用案例和相关概念的对比,力求全面理解并灵活运用 ROC 和 AUC。

- 基础概念介绍
1.1 什么是 ROC 曲线
ROC 曲线,即接收者操作特征曲线,ROC曲线产生于第二次世界大战期间,最早用在信号检测领域,侦测战场上的敌军载具(飞机、船舰)。现在是是用来评价二分类模型性能的常用图形工具。它通过显示真阳性率(True Positive Rate,简称 TPR)与假阳性率(False Positive Rate,简称 FPR)之间的权衡来帮助我们理解模型的分类能力。
1.2 什么是 AUC
AUC,即曲线下面积(Area Under Curve),是 ROC 曲线下面积的一个数值表示。它提供了一个定量的指标,用来衡量分类模型的整体表现。AUC 值范围从 0 到 1,值越大表示模型性能越好。
1.3 为何需要 ROC/AUC
在分类任务中,特别是当数据集类别不平衡时,单纯依赖准确率(Accuracy)可能会造成误导。为了更好地理解这一点,让我们通过一个例子来说明。
例子说明
假设我们有一个武侠元素的数据集,其中 95% 的样本是普通弟子,5% 的样本是高手。
让我们通过代码示例来演示这一点(代码供复现使用,可直接跳过下滑到解释部分):
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, roc_auc_score, accuracy_score, confusion_matrix
生成一个极度不平衡的武侠数据集
假设特征表示武功修炼时间、战斗胜率等,标签表示是否为高手
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, weights=[0.95, 0.05], random_state=42)
将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
创建一个总是预测普通弟子的模型
class AlwaysNegativeModel:
def predict(self, X):
return np.zeros(X.shape[0])
训练和预测
model = AlwaysNegativeModel()
y_pred = model.predict(X_test)
计算混淆矩阵和准确率
cm = confusion_matrix(y_test, y_pred)
accuracy = accuracy_score(y_test, y_pred)
计算 ROC 曲线和 AUC
在这里我们需要一个概率预测来计算 ROC 曲线和 AUC,为了演示,我们假设模型输出的是一个常量概率
y_pred_prob = np.zeros(X_test.shape[0])
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
auc = roc_auc_score(y_test, y_pred_prob)
可视化结果
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title(“混淆矩阵”)
plt.imshow(cm, interpolation=‘nearest’, cmap=plt.cm.Blues)
plt.colorbar()
plt.xlabel(“预测标签”)
plt.ylabel(“真实标签”)
plt.xticks([0, 1], [“普通弟子”, “高手”])
plt.yticks([0, 1], [“普通弟子”, “高手”])
for i in range(2):
for j in range(2):
plt.text(j, i, cm[i, j], ha=“center”, va=“center”, color=“red”)
print(f"准确率: {accuracy:.2f}“)
print(f"AUC: {auc:.2f}”)
结果分析
如果我们使用一个简单的分类器,它总是预测所有样本为普通弟子。
这个模型的准确率为 95%,看起来表现很好,但实际上它根本无法识别高手,是一个毫无用处的分类器。
这个分类器没有任何实际的分类能力,因为它无法识别出真正的高手。
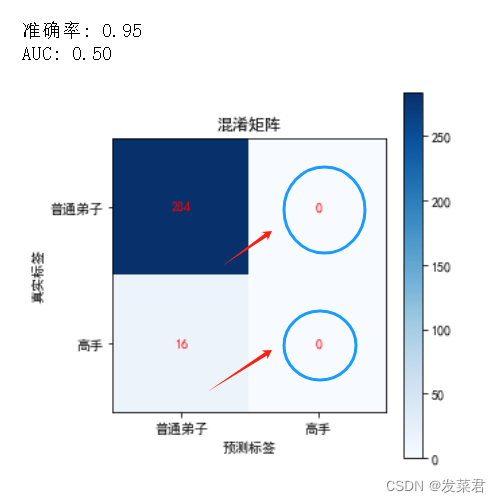
ROC 曲线和 AUC:通过绘制 ROC 曲线并计算 AUC,我们可以看到 AUC 为 0.50,这表明模型没有任何区分能力。ROC 曲线是一条对角线,显示模型在随机猜测。
准确率只告诉我们模型整体预测正确的比例,但在类别不平衡的情况下,这个指标可能会误导我们。ROC 曲线和 AUC 提供了更全面的视角,展示了模型在不同阈值下的性能,帮助我们更准确地评估模型的分类能力。
2. 详细解释
2.1 TPR(True Positive Rate)和 FPR(False Positive Rate)的定义
要理解 ROC 曲线,首先需要明白 TPR 和 FPR 的概念:
TPR(True Positive Rate):也称为灵敏度(Sensitivity)或召回率(Recall),表示的是在所有真实为正的样本中,被正确预测为正的比例。其计算公式为:
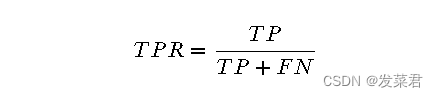
其中,TP(True Positives)是将正类正确分类为正类的样本数,FN(False Negatives)是将正类错误分类为负类的样本数。
FPR(False Positive Rate):表示的是在所有真实为负的样本中,被错误预测为正的比例。其计算公式为:
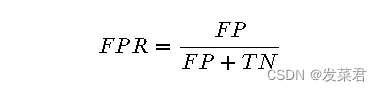
其中,FP(False Positives)是将负类错误分类为正类的样本数,TN(True Negatives)是将负类正确分类为负类的样本数。
2.2 AUC 的数学定义
AUC(Area Under Curve)是 ROC 曲线下的面积,用于评估分类模型的性能。AUC 值的范围从 0 到 1,值越大表示模型的性能越好。
数学上,AUC 可以通过积分计算:
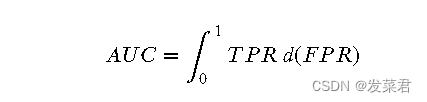
在离散情况下,AUC 可以通过梯形法则近似计算:
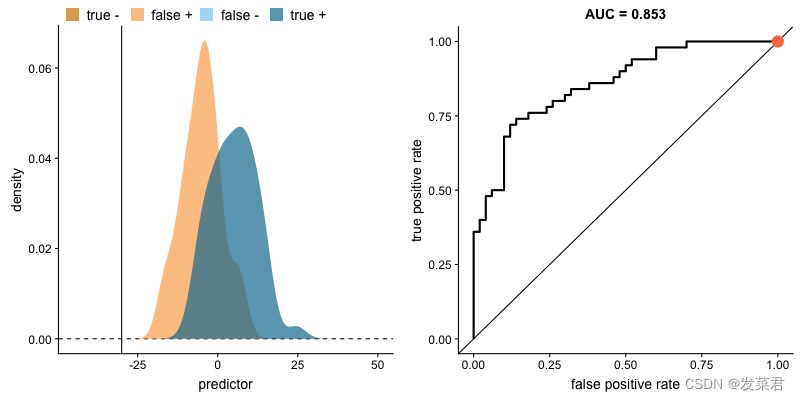
3 绘制 ROC 曲线的步骤
绘制 ROC 曲线的步骤如下:
选择阈值:从 0 到 1 的不同阈值。
计算 TPR 和 FPR:对于每个阈值,计算相应的 TPR 和 FPR。
绘制曲线:以 FPR 为横轴,TPR 为纵轴,绘制 ROC 曲线。
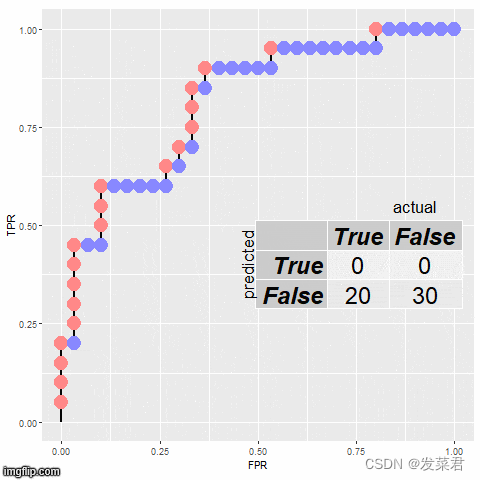
选择阈值:从 0 到 1 的不同阈值
from sklearn.metrics import roc_curve
预测测试集概率
y_pred_prob = model.predict_proba(X_test)[:, 1]
计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
输出部分阈值
print("阈值: ", thresholds[:10]) # 仅展示前10个阈值
计算 TPR 和 FPR:对于每个阈值,计算相应的 TPR 和 FPR
输出部分阈值对应的 TPR 和 FPR
for i in range(10): # 仅展示前10个阈值的对应值
print(f"阈值: {thresholds[i]:.2f} -> 假阳性率 (FPR): {fpr[i]:.2f}, 真阳性率 (TPR): {tpr[i]:.2f}")
绘制曲线:以 FPR 为横轴,TPR 为纵轴,绘制 ROC 曲线
import matplotlib.pyplot as plt
可视化 ROC 曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color=‘blue’, lw=2, label=‘ROC 曲线’)
plt.plot([0, 1], [0, 1], color=‘gray’, lw=1, linestyle=‘–’, label=‘随机猜测’)
plt.xlabel(“假阳性率 (FPR)”)
plt.ylabel(“真阳性率 (TPR)”)
plt.title(“ROC 曲线”)
plt.legend(loc=“lower right”)
在曲线上标出几个阈值点
threshold_points = [0.2, 0.5, 0.8]
for threshold in threshold_points:
idx = np.where(thresholds >= threshold)[0][0]
plt.scatter(fpr[idx], tpr[idx], marker=‘o’, color=‘red’)
plt.text(fpr[idx], tpr[idx], f"阈值={threshold:.2f}", fontsize=12)
plt.show()
plt.subplot(1, 2, 2)
plt.title(“AUC 值示意”)
plt.fill_between(fpr, tpr, color=‘blue’, alpha=0.3)
plt.plot(fpr, tpr, color=‘blue’, lw=2, label=f"AUC = {auc:.2f}")
plt.xlabel(“假阳性率”)
plt.ylabel(“真阳性率”)
plt.legend(loc=“lower right”)
plt.tight_layout()
plt.show()
print(f"AUC: {auc:.2f}")
那么,我们该如何学习大模型?
作为一名热心肠的互联网老兵,我决定把宝贵的AI知识分享给大家。 至于能学习到多少就看你的学习毅力和能力了 。我已将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。
一、大模型全套的学习路线
学习大型人工智能模型,如GPT-3、BERT或任何其他先进的神经网络模型,需要系统的方法和持续的努力。既然要系统的学习大模型,那么学习路线是必不可少的,下面的这份路线能帮助你快速梳理知识,形成自己的体系。
L1级别:AI大模型时代的华丽登场
L2级别:AI大模型API应用开发工程
L3级别:大模型应用架构进阶实践

L4级别:大模型微调与私有化部署

一般掌握到第四个级别,市场上大多数岗位都是可以胜任,但要还不是天花板,天花板级别要求更加严格,对于算法和实战是非常苛刻的。建议普通人掌握到L4级别即可。
以上的AI大模型学习路线,不知道为什么发出来就有点糊,高清版可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

二、640套AI大模型报告合集
这套包含640份报告的合集,涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师,还是对AI大模型感兴趣的爱好者,这套报告合集都将为您提供宝贵的信息和启示。

三、大模型经典PDF籍
随着人工智能技术的飞速发展,AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型,如GPT-3、BERT、XLNet等,以其强大的语言理解和生成能力,正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。
四、AI大模型商业化落地方案

作为普通人,入局大模型时代需要持续学习和实践,不断提高自己的技能和认知水平,同时也需要有责任感和伦理意识,为人工智能的健康发展贡献力量。
相关文章:

一文彻底理解机器学习 ROC-AUC 指标
在机器学习和数据科学的江湖中,评估模型的好坏是非常关键的一环。而 ROC(Receiver Operating Characteristic)曲线和 AUC(Area Under Curve)正是评估分类模型性能的重要工具。 这个知识点在面试中也很频繁的出现。尽管…...

【二】【动态规划NEW】91. 解码方法,62. 不同路径,63. 不同路径 II
91. 解码方法 一条包含字母 A-Z 的消息通过以下映射进行了 编码 : ‘A’ -> “1” ‘B’ -> “2” … ‘Z’ -> “26” 要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法ÿ…...

Python闯LeetCode--第3题:无重复字符的最长子串
Problem: 3. 无重复字符的最长子串 文章目录 思路解题方法复杂度Code 思路 一上来马上想到两层for循环暴力枚举,但是又立马想到复杂度是 O ( n 2 ) O(n^2) O(n2),思考了一下能否有更优解,于是想到用头尾两个指针来指定滑动窗口(主…...

HTML DOM 对象
HTML DOM 对象 1. 概述 HTML DOM(文档对象模型)是一个跨平台和语言独立的接口,它允许程序和脚本动态地访问和更新文档的内容、结构和样式。在HTML DOM中,文档被表示为节点树,其中每个节点代表文档中的一个部分,例如元素、文本或属性。HTML DOM对象是构成这个节点树的基…...

如何解决 BeautifulSoup 安装问题:从 BeautifulSoup 3 到 BeautifulSoup 4
在使用 Python 的过程中,解析 HTML 和 XML 数据是一项常见任务。BeautifulSoup 是一个非常流行的解析库。然而,最近在安装 BeautifulSoup 时,遇到了一些问题。本文将介绍如何解决这些问题,并成功安装 BeautifulSoup 4。 问题描述 …...

原型模式--深复制/浅复制
原型模式用于克隆复杂对象,由于new一个实例对象会消耗大部分时间,所以原型模式可以节约大量时间 1 public class Sheep implements Cloneable{2 private String name;3 private Date birth;4 public Sheep(String name, Date birth) {5 …...
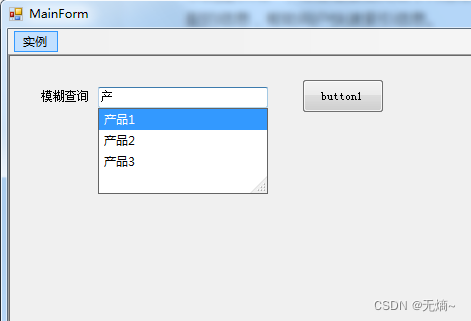
C# TextBox模糊查询及输入提示
在程序中,我们经常会遇到文本框中不知道输入什么内容,这时我们可以在文本框中显示提示词提示用户;或者需要查询某个内容却记不清完整信息,通常可以通过文本框列出与输入词相匹配的信息,帮助用户快速索引信息。 文本框…...
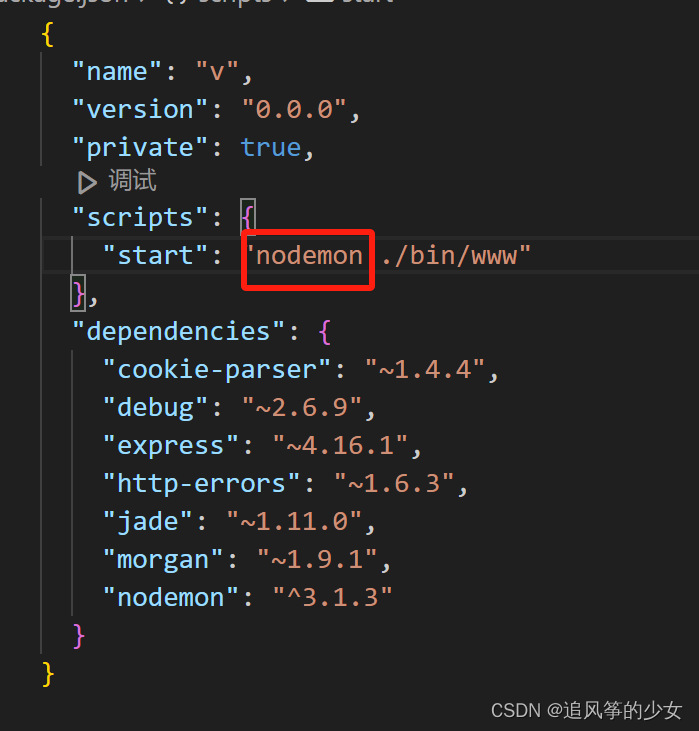
Node入门以及express创建项目
前言 记录学习NodeJS 一、NodeJS是什么? Node.js 是一个开源和跨平台的 JavaScript 运行时环境 二、下载NodeJs 1.下载地址(一直点击next即可,记得修改安装地址) https://nodejs.p2hp.com/download/ 2.查看是否安装成功,打开命令行 nod…...
Cheat Engine CE v7.5 安装教程(专注于游戏的修改器)
前言 Cheat Engine是一款专注于游戏的修改器。它可以用来扫描游戏中的内存,并允许修改它们。它还附带了调试器、反汇编器、汇编器、变速器、作弊器生成、Direct3D操作工具、系统检查工具等。 一、下载地址 下载链接:http://dygod/source 点击搜索&…...
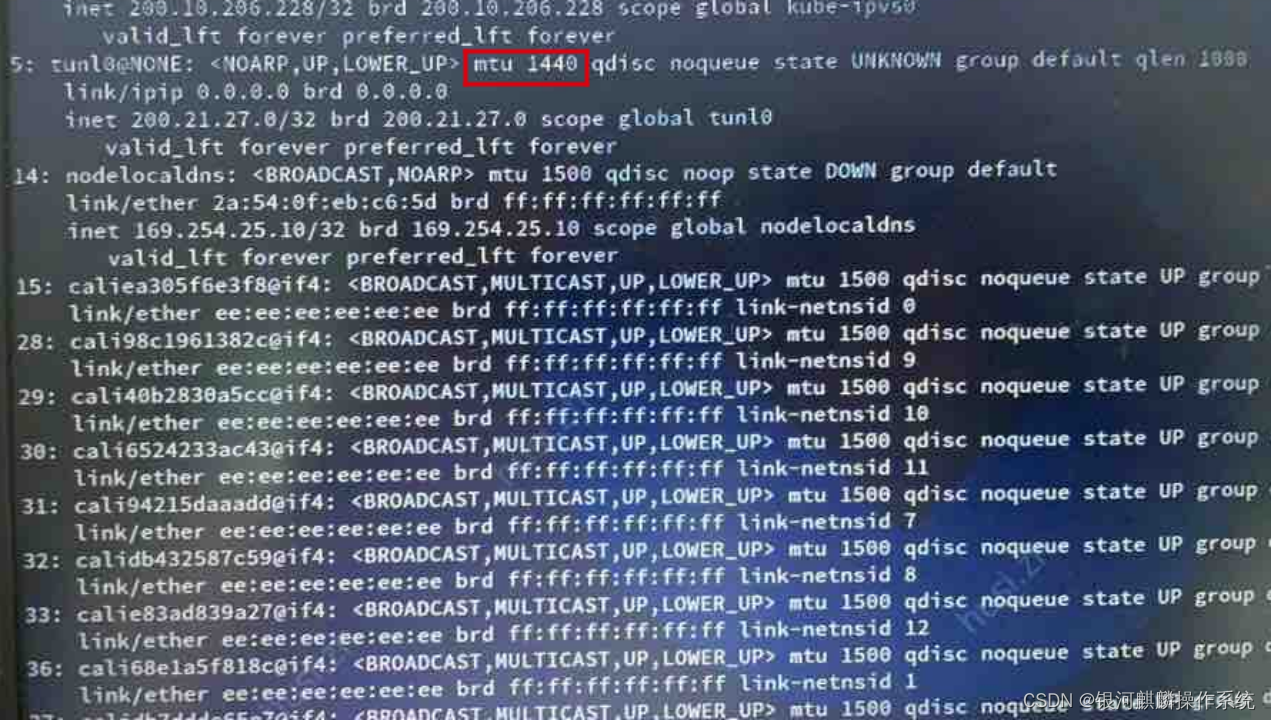
【实例分享】访问后端服务超时,银河麒麟服务器操作系统分析及处理建议
1.服务器环境以及配置 【机型】 处理器: Intel 32核 内存: 128G 整机类型/架构: x86_64虚拟机 【内核版本】 4.19.90-25.22.v2101.kylin.x86_64 【OS镜像版本】 kylin server V10 SP2 【第三方软件】 开阳k8s 2.问题现象描述 …...

Java中和的区别
在Java中,& 和 && 都是逻辑运算符,但它们之间存在一些重要的区别,特别是在它们如何评估其操作数以及它们的性能影响方面。 短路评估(Short-Circuit Evaluation): &&(逻辑…...
深入理解计算机系统 CSAPP 家庭作业6.34
第一步先求(S,E,B,m) 题目说共C32个字节,块大小B为16个字节,那就是分为两组:0,1.然后每组存4个int 每个4字节 CB*E*S .B16 ,直接映射的E就是1,所以S2 m为啥等于7? 通过写出两个数组所有的地址可以得出m7. 得出高速缓存的参数:(S,E,B,m)(2,1,16,7),注意图6-26每个参数的定义…...

[leetcode 141环形链表]双指针解决环形链表
Problem: 141. 环形链表 文章目录 思路Code 思路 首先想到如果链表为空直接返回false 其次想到用双指针,一个一回走一步,另一个一回走两步 如果是环形,总有一个时刻,两指针会指向同一个节点,而且该结点不能为空(空是快指针遍历完单链表了) Code /*** Definition for singly-li…...

【深度学习】Precision、Accuracy的区别,精确率与准确率:深度学习多分类问题中的性能评估详解
在深度学习的多分类问题中,Precision(精确率)和Accuracy(准确率)是两种常用的性能评估指标,它们各自有不同的定义和用途。 Precision(精确率)的中文发音是:pǔ rēi xī…...
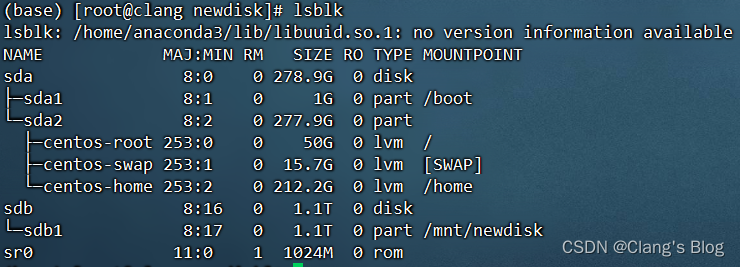
DELL服务器插入新磁盘、创建虚拟磁盘、挂载磁盘步骤
文章目录 一、磁盘清理(可选,针对新硬盘是Foreign状态)1、进入VD Mgmt2、清理新硬盘配置 二、创建虚拟磁盘1、进入Device Settings2、创建虚拟磁盘 三、挂载磁盘到系统1、分区磁盘(注意实际磁盘的名称)2、格式化分区3、…...

springboot与flowable(10):网关服务(排他网关)
一、绘制流程图 排他网关用于对流程中的决策建模。当执行到这个网关时,会按照所有出口顺序流定义的顺序对它们进行计算。选择第一个条件为true的顺序流继续流程。例如员工请假时,小于等于3天由组长审批,大于3天由总监审批。流程案例ÿ…...

Web前端网页源代码:深入剖析与实用技巧
Web前端网页源代码:深入剖析与实用技巧 在Web开发的浩瀚领域中,前端网页源代码扮演着至关重要的角色。它不仅是网页的骨架,更是实现各种交互和视觉效果的基石。本文将从四个方面、五个方面、六个方面和七个方面,对Web前端网页源代…...

聊天页面样式
聊天页面样式 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><link rel"styleshee…...

PHP入门教程3:数组和字符串操作
PHP入门教程3:数组和字符串操作 在前两篇文章中,我们学习了PHP的基础语法、控制结构和函数的使用。本文将重点介绍数组和字符串的高级操作,这些是PHP编程中非常常见且重要的内容。本文将包含以下几个部分: 数组的类型和操作多维…...

mariadb
MariaDB安装配置、使用、授权、增删改查以及数据库备份与恢复 MariaDB安装配置、使用、授权、增删改查以及数据库备份与恢复_mariadb安装及配置教程-CSDN博客mariadb 恢复: ERROR! MySQL server PID file could not be found! 170104 23:04:21 InnoDB: The InnoD…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
