代码随想录算法训练营Day37|56.合并区间、738.单调递增的数字、968.监控二叉树
合并区间
56. 合并区间 - 力扣(LeetCode)
和之前的思路类似,先创建一个ans二维数组,创建start和end来指明添加进入ans数组的区间下标,先对数组按照首元素排序从小到大排序后,根据当前元素是否小于下一个元素的第一个元素来决定将这个对ans数组进行增加、移动下标或改变end。具体代码如下。
class Solution {
public:// 定义一个比较函数,用于sort函数,按照区间的起始点进行排序static bool cmp(vector<int>&a, vector<int>&b){return a[0]<b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {// 使用sort函数和自定义的比较函数cmp对区间进行排序sort(intervals.begin(),intervals.end(),cmp);// 定义一个二维向量用于存放合并后的区间vector<vector<int>>ans;// 如果输入的区间为空,直接返回空的ansif(intervals.size() == 0){return ans;}// 如果只有一个区间,直接将该区间放入ans中if(intervals.size() == 1){ans.push_back(vector<int>{intervals[0][0],intervals[0][1]});return ans;}// 初始化起始和结束点为第一个区间的起始和结束点int begin = intervals[0][0];int end = intervals[0][1];for(int i = 0 ; i < intervals.size()-1; i++){// 如果当前区间的起始点大于上一个区间的结束点,说明没有重叠if(intervals[i+1][0] > end){// 将上一个区间加入ans中ans.push_back(vector<int>{begin,end});// 更新区间的起始和结束点为当前区间的起始和结束点begin = intervals[i+1][0];end = intervals[i+1][1];}else// 如果有重叠,更新结束点为当前区间和上一个区间结束点的较大值end = max(intervals[i+1][1],end);// 如果是最后一个区间,将其加入ans中if(i == intervals.size()-2){ans.push_back(vector<int>{begin,end});} }// 返回合并后的区间return ans;}
};
算法的时间复杂度为O(nlogn),空间复杂度为O(n)。
代码随想录中代码
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> result;if (intervals.size() == 0) return result; // 区间集合为空直接返回// 排序的参数使用了lambda表达式sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});// 第一个区间就可以放进结果集里,后面如果重叠,在result上直接合并result.push_back(intervals[0]); for (int i = 1; i < intervals.size(); i++) {if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间// 合并区间,只更新右边界就好,因为result.back()的左边界一定是最小值,因为我们按照左边界排序的result.back()[1] = max(result.back()[1], intervals[i][1]); } else {result.push_back(intervals[i]); // 区间不重叠 }}return result;}
};- 时间复杂度: O(nlogn)
- 空间复杂度: O(logn),排序需要的空间开销
单调递增的数字
738. 单调递增的数字 - 力扣(LeetCode)
贪心算法,98的最小单调递增数字为89,第一位不符合单调递增的情况,将该值--,并将后面的数字都变为9,使用字符串可以方便对数字进行处理,所以我们先将数字转换为字符串,然后寻找到第一个不符合单调递增情况的数字,之后对该数字以前的数字全部-1,保证其前几位在符合单调递增的情况下最大,最后把后面的数字全部变为9,即实现了最大的单调递增数字。
class Solution {
public:int monotoneIncreasingDigits(int n) {// 将整数n转换为字符串s,以便逐位处理string s = to_string(n);int i = 1;// 从左到右遍历字符串,直到遇到一个位置i,使得s[i-1] > s[i]// 找到需要调整的位置while(i < s.size() && s[i-1]<=s[i]){i++;}// 如果i没有遍历到字符串的末尾,说明我们找到了需要调整的位置if(i < s.size()){// 从位置i开始,向前遍历,直到s[i-1]不再大于s[i]// 将每个大于其后继的数字减1,这样可以保证数字尽可能大且单调递增while(i > 0 && s[i-1] > s[i]){s[i - 1] -= 1;i-- ; }// 将位置i之后的所有数字都置为'9',这样可以保证这些位置的数字是最大的for(int j = i + 1; j < s.size(); j++){s[j] = '9';}}// 将处理后的字符串s转换回整数并返回return stoi(s);}
};
时间复杂度为O(n),空间复杂度为O(n)。
监控二叉树
968. 监控二叉树 - 力扣(LeetCode)
我开始的想法是用一个层序遍历,然后将偶数层的节点相加得到监控的数目,有些问题,后面再改改。(能力不够,先跳过吧)
class Solution {
public:int minCameraCover(TreeNode* root) {queue<TreeNode*> queue;if(root!=nullptr){queue.push(root);}int count = 0;int flag = 0;TreeNode*cur = root;vector<int>ans;while(!queue.empty()){int size = queue.size();ans.push_back(size);for(int i = 0; i < size; i++){cur = queue.front();queue.pop();if(cur->left){queue.push(cur->left);}if(cur->right){queue.push(cur->right);}}}if(ans.size() <= 2){return 1;}for(int i = 1 ; i < ans.size(); i = i + 2){count += ans[i];}return count;}
};代码随想录思路
代码随想录 (programmercarl.com)一个监控摄像头最多可以监控父节点、自己和两个子节点,累计三层,若想要最小化摄像头的数目,最优的方式必定要利用好这个特点。叶节点远多于根节点,考虑在叶节点处节约摄像头的数目,选择叶节点的父节点作为摄像头的放置位置。遍历到根节点再放置一个摄像头,所以使用后序遍历。
贪心算法,二叉树与贪心的结合,有点难...... LeetCode:968.监督二叉树_哔哩哔哩_bilibili
思路不好想啊。。。。
二叉树中的每个节点有3个状态。0.无覆盖、1.有摄像头、2.有覆盖
后序遍历,从叶节点往上遍历,总共有四种情况。
1.左右孩子都有覆盖,返回0,此处为无覆盖
2.左右节点存在无覆盖情况,必须放入一个摄像头
3.左右至少存在一个摄像头,当前位置状态为有覆盖
4.根节点状态为无覆盖,放置一个摄像头。
class Solution {
private:int result;int traversal(TreeNode* cur) {// 空节点,该节点有覆盖if (cur == NULL) return 2;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右// 情况1// 左右节点都有覆盖if (left == 2 && right == 2) return 0;// 情况2// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头,右节点无覆盖// left == 0 && right == 1 左节点有无覆盖,右节点摄像头// left == 0 && right == 2 左节点无覆盖,右节点覆盖// left == 2 && right == 0 左节点覆盖,右节点无覆盖if (left == 0 || right == 0) {result++;return 1;}// 情况3// left == 1 && right == 2 左节点有摄像头,右节点有覆盖// left == 2 && right == 1 左节点有覆盖,右节点有摄像头// left == 1 && right == 1 左右节点都有摄像头// 其他情况前段代码均已覆盖if (left == 1 || right == 1) return 2;// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解// 这个 return -1 逻辑不会走到这里。return -1;}public:int minCameraCover(TreeNode* root) {result = 0;// 情况4if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};算法时间复杂度为O(n),空间复杂度O(n)。
相关文章:

代码随想录算法训练营Day37|56.合并区间、738.单调递增的数字、968.监控二叉树
合并区间 56. 合并区间 - 力扣(LeetCode) 和之前的思路类似,先创建一个ans二维数组,创建start和end来指明添加进入ans数组的区间下标,先对数组按照首元素排序从小到大排序后,根据当前元素是否小于下一个元…...

Web前端开发12章:深入探索与实战解析
Web前端开发12章:深入探索与实战解析 在数字化浪潮的推动下,Web前端开发技术日新月异,成为了构建互联网应用的重要基石。本文将以12章的篇幅,从四个方面、五个方面、六个方面和七个方面,深入探索Web前端开发的精髓&am…...

八股操作系统和计算机网络
5.线程间的同步的方式有哪些? 6.PCB(不熟悉) 进程状态 什么是僵尸进程和孤儿进程? 进程调度算法 死锁的理解 举个发生死锁的例子 解决死锁的方式 内存管理做了哪些事情 什么是内存碎片 常见的内存管理 段表通过什么数据结构实现地址映射 分段机制为什么会…...

正能量情感语录热门素材文案去哪里找?文案素材网站分享
正能量情感语录热门素材文案去哪里找?文案素材网站分享 想为你的作品注入正能量和情感温度?不知如何获取热门情感语录素材?别担心,今天我将为大家推荐一些海外知名的素材网站,让你轻松找到受欢迎的文案素材ÿ…...
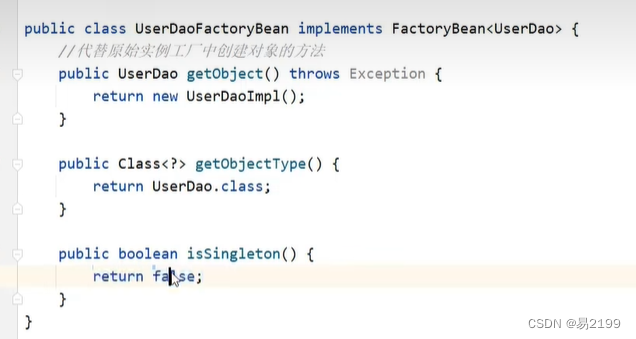
bean实例化
黑马程序员SSM 文章目录 一、bean是如何创建的二、实例化bean的三种方式3.1 构造方法(常用)3.2 静态工厂3.3 实例化工厂(了解)3.4 FactoryBean 一、bean是如何创建的 Spring 创建bean的时候使用的是无参构造 二、实例化bean的三…...

Django中间件探索:揭秘中间件在Web应用中的守护角色与实战应用
系列文章目录 Django入门全攻略:从零搭建你的第一个Web项目Django ORM入门指南:从概念到实践,掌握模型创建、迁移与视图操作Django ORM实战:模型字段与元选项配置,以及链式过滤与QF查询详解Django ORM深度游ÿ…...

【PL理论】(24) C- 语言:有块的作用域 | 更新的语法 | 新的语义域 | 环境 vs. 内存
💭 写在前面:我们将再次扩展之前的C语言,让我们向这种语言引入“作用域”的概念。 目录 0x00 C- 语言:有块的作用域 0x01 C- 语言:更新的语法 0x02 新的语义域 0x03 环境 vs. 内存 0x00 C- 语言:有块的…...

React native 使用Animated 优化连续setState 性能问题
再部分场景下我们需要连续更新state刷新页面。一般情况刷新使用setstate没有问题,当需要连续刷新的情况会有明显的性能问题。 场景:自定义可拖动抽屉组件 新增需求在抽屉活动是更新主页面组件样式,此时需要动态传递抽屉高度修改主页组件属性…...

Qt中的事件循环
Gui框架一般都是基于事件驱动的,Qt也不例外,在 Qt 框架中,事件循环(Event Loop)是一个核心机制,负责管理和分发应用程序中的所有事件和消息。它确保了应用程序能够响应用户输入、定时器事件、窗口系统事件等…...
)
JVM常用概念之线程本地分配缓冲区(ThreadLocal Allocation Buffer,TLAB)
当实例化一个Java类时,运行时环境必须为相关实例分配存储空间,在JRE中此存储空间分配操作是由内存管理器实现的(其实是JVM的垃圾回收器),由于内存管理器通常使用与运行时目标语言不同的语言编写(例如&#…...

大模型生成的常见Top-k、Top-p、Temperature参数
参考: https://zhuanlan.zhihu.com/p/669661536 topK,topP https://www.douyin.com/video/7380126984573127945 主要是softmax产生的词表每个词的概率分布后, topK,比如K3,表示采样概率最大的前3个,其他全…...

ppt添加圆角矩形,并调整圆角弧度方法
一、背景 我们看的论文,许多好看的图都是用PPT做的,下面介绍用ppt添加圆角矩形,并调整圆角弧度方法。 二、ppt添加圆角矩形,并调整圆角弧度 添加矩形: 在顶部工具栏中,点击“插入”选项卡。 在“插图”…...

测评要求+基本措施+对应产品
基本要求项测评项基本措施对应产品 网络架构 网络架构 网络架构应保证网络各个部分的带宽满足业务高峰期需要;带宽管理流量控制系统 网络架构 网络架构 网络架构应避免将重要网络区域部署在边界处,重要网络区域与其他网络区域之间应采取可靠的技术隔离手…...

什么是git?
前言 Git 是一款免费、开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。是的,我对git的介绍就一条,想看简介的可以去百度一下😘😘😘 为什么要用git? OK,想象一下…...
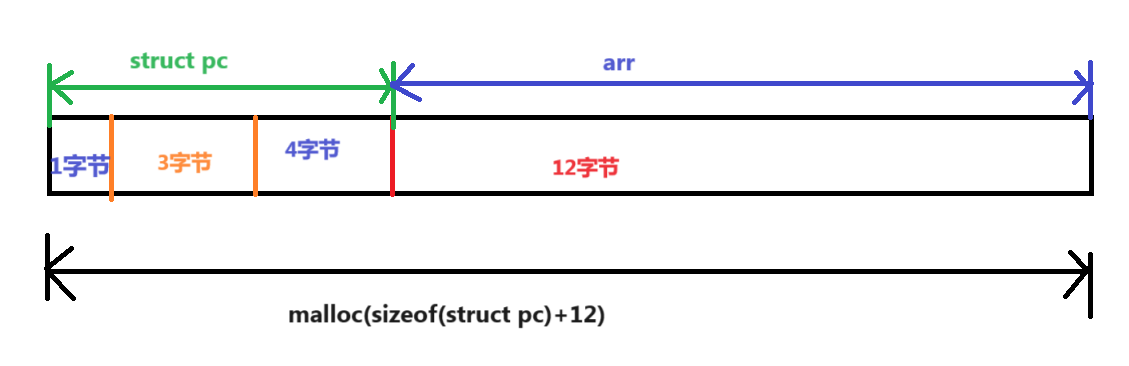
C/C++中内存开辟与柔性数组
C/C中内存的开辟 在C中,我们都知道有三个区: 1. 栈区(stack):在执行函数时,函数内局部变量的存储单元都可以在栈上创建,函数执行结 束时这些存储单元自动被释放。栈内存分配运算内置于处理器的指…...

编程App软件优化是什么
编程App软件优化是什么 在数字化时代,编程App软件已成为我们日常生活和工作中不可或缺的一部分。然而,随着技术的不断进步和用户需求的日益多样化,如何对编程App软件进行优化,以提供更高效、更流畅的用户体验,成为了开…...

爱了爱了,11款超良心App推荐!
AI视频生成:小说文案智能分镜智能识别角色和场景批量Ai绘图自动配音添加音乐一键合成视频https://aitools.jurilu.com/今天,我们向你推荐十款与众不同但又不错的win10软件,它们都有各自的功能和优点,相信你一定会喜欢。 1.图片处…...
(文件、权限等))
Linux基础指令(二)(文件、权限等)
目录 普通文件的操作 touch cat 翻页 标准输出重定向: 标准输出重定向种类: 管道符:| 压缩指令: zip gzip tar Linux下最常见的打包指令 其他系统指令: 快捷…...

爆火的治愈系插画工具又来了,额度居然有18w,根本花不完?
AI治愈插画又又又来了 今天给大家推荐一款完全免费的软件,用过的人都说好! 先来看看我生成的图 制作过程非常简单,输入你想要生成的画面咒语。 工具地址:https://www.qiyuai.net/ 模型目前有两种 我上面的图就是用的第一种通用…...
信号与槽 | 4.3、信号连接信号)
Qt 实战(4)信号与槽 | 4.3、信号连接信号
文章目录 一、信号连接信号1、什么是信号连接信号?2、如何实现信号连接信号3、总结 前言: 在Qt框架中,信号与槽(Signals and Slots)机制是对象间通信的核心。通常情况下,我们习惯于将信号连接到槽函数上&am…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
