C语言王国——数组的旋转(轮转数组)三种解法
目录
一、题目
二、分析
2.1 暴力求解法
2.2 找规律
2.3 追求时间效率,以空间换时间
三、结论
一、题目
给定一个整数数组
nums,将数组中的元素向右轮转k个位置,其中k是非负数。示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
二、分析
2.1 暴力求解法
这题是旋转字符串但是它的实质是将前面n-1个数据往后移一位,然后将最后一个数据移到第一个,旋转几次则执行几次这个步骤。为了变量不被覆盖,变量采取从后向前移动,而最后一个数据利用一个空变量temp去拷贝一份,在前面数据移动完成后则拷贝到第一个数据。如下面代码:
void rotate(int* num ,int k , int size)
{k %= size;//size次一次循环while (k){int temp = num[size-1];for (int i = size-1; i > 0; i--){num[i] = num[i - 1];}num[0] = temp;k--;}
}int main()
{int arr[] = { 7,1,2,3,4,5,6 };int size = sizeof(arr) / sizeof(arr[0]);int k = 1;printf("旋转几次数组:");scanf("%d", &k);printf("旋转前:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}rotate(arr, k, size);printf("\n旋转后为:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
}2.2 找规律
我们发现暴力求解虽然可以解出此题,但是时间复杂度,那我们有什么办法去降低时间复杂度呢?我们可以尝试降低它的循环次数,找找看他们有什么规律?
如图,将前面n-k个数字逆置然后将后面n个逆置,然后将他们整体逆置。(红色位将要进行逆置的数)

代码如下:
void Inversion(int* arr, int l, int r)
{while (l < r){int temp = arr[l];arr[l] = arr[r];arr[r] = temp;l++;r--;}
}void rotate(int* nums, int numsSize, int k) {k %= numsSize;//不让数组越界,完成一次数组长度的旋转数组不变Inversion(nums, 0, numsSize - k - 1);Inversion(nums, numsSize - k, numsSize - 1);Inversion(nums, 0, numsSize - 1);
}int main()
{int arr[] = { 7,1,2,3,4,5,6 };int size = sizeof(arr) / sizeof(arr[0]);int k = 1;printf("旋转几次数组:");scanf("%d", &k);printf("旋转前:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}rotate(arr, size, k);printf("\n旋转后为:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
}*这里要注意数组越界访问,我们发现数组完成一次数组长度的旋转,数组不变,所以我们取模于数组长度。
2.3 追求时间效率,以空间换时间
这里我们不讨论空间复杂度只优化时间复杂度,所以我们可以新开辟一段空间,将后n个旋转的数字先放入我们开辟的空间,然后再将前面的n-k个数字放入空间后面。
如代码:
void rotate(int* nums, int numsSize, int k) {k %= numsSize;int* temp = (int*)malloc(sizeof(int) * numsSize);memcpy(temp, nums + numsSize - k, sizeof(int) * k);memcpy(temp + k, nums, sizeof(int) * (numsSize - k));memcpy(nums, temp, sizeof(int) * numsSize);free(temp);//释放临时空间temp = NULL;
}int main()
{int arr[] = { 7,1,2,3,4,5,6 };int size = sizeof(arr) / sizeof(arr[0]);int k = 1;printf("旋转几次数组:");scanf("%d", &k);printf("旋转前:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}rotate(arr, size, k);printf("\n旋转后为:");for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
}三、结论
每一道题都有属于自己的空间和时间复杂度,当你写出一段代码的时候去想想还能不能继续去优化它,使它的时间和空间复杂度更小。姜糖在这里就是不断在优化它的时间复杂度,从O(N^2)到最后的O(N)。如果大家还有什么不同的看法可以跟姜糖展开讨论哦。
相关文章:

C语言王国——数组的旋转(轮转数组)三种解法
目录 一、题目 二、分析 2.1 暴力求解法 2.2 找规律 2.3 追求时间效率,以空间换时间 三、结论 一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出…...

MySQL中CAST和CONVERT函数都用于数据类型转换
在 MySQL 中,CAST() 和 CONVERT() 函数都用于数据类型转换。虽然这两个函数在大多数情况下可以互换使用,但它们之间还是有一些细微的差别。 官方文档地址 https://dev.mysql.com/doc/refman/8.4/en/cast-functions.html#function_cast CAST() 函数 C…...

速盾:cdn影响seo吗?
CDN (Content Delivery Network) 是一个分布式网络架构,用于在全球范围内加速网站内容的传输和分发。它通过将网站的静态资源(例如图片、CSS、JavaScript 文件等)存储在多个服务器上,使用户可以从最接近他们位置的服务器上获取这些…...
期末算法复习
0-1背包问题(动态规划) 例题 算法思想: 动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。 主要是状态转移方程和状态 算法描述: 初始化一个二维数组dp࿰…...

可穿戴设备:苹果“吃老底”、华为“忙复苏”、小米“再扩容”
配图来自Canva可画 随着产品功能的创新,可穿戴设备不再被简单地视为手机的延伸,而是被当成一种独立的、具有独特功能和优势的产品,受到了越来越多人的青睐。 一方面,技术的进步使得可穿戴设备在功能、性能和使用体验上得到显著提…...

AI数据分析:集中度分析和离散度分析
在deepseek中输入提示词: 你是一个Python编程专家,要完成一个Python脚本编写的任务,具体步骤如下: 读取Excel表格:"F:\AI自媒体内容\AI行业数据分析\toolify月榜\toolify2023年-2024年月排行榜汇总数据.xlsx&qu…...

redis的分布式session和本地的session有啥区别
在web应用开发中,Session用于在多个请求之间存储用户数据。传统上,Session存储在服务器的内存中,即本地Session。然而,随着应用规模和复杂度的增加,特别是在分布式环境中,本地Session会遇到一些问题。这时&…...

SSH概念、用途、详细使用方法
还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas,webgl,ech…...
关于电脑文件的规划思考
概述 设置C、D、E、F 四个盘 C盘:系统数据使用,操作系统、其他软件需要用到的系统性资源 D盘:应用软件区 的使用,数据库、navacat、idea、visual studio、浏览器、向日葵、虚拟机…… E盘:工作区:公司资料…...
DVWA - Brute Force
DVWA - Brute Force 等级:low 直接上bp弱口令爆破,设置变量,攻击类型最后一个,payload为用户名、密码简单列表 直接run,长度排序下,不一样的就是正确的用户名和密码 另解: 看一下…...
安卓手机文件找回方法汇总,3个技巧,不再焦虑
我们用手机来储存各种重要的信息和文件,无论是珍贵的照片、重要的文档还是喜爱的音乐,用来记录和分享生活中的每一个瞬间。但如果不小心删除了这些文件,我们可能会面临数据丢失的风险,进而产生焦虑和不安。本文将为您揭秘手机文件…...

{}初始化
文章目录 ()初始化的问题易混淆弱检查 {}初始化{}初始化是c11推荐的初始化,解决了上述的问题 ()则被用于强制类型转换 ()初始化的问题 易混淆 string s();不能确定是函数定义还是对象定义 弱检查 int a(3.14);3.14 可以通过 int 定义 {}初始化 {}初始化是c11推…...

小程序外卖开发中的关键技术与实现方法
小程序外卖服务凭借其便捷性和灵活性,正成为现代餐饮行业的重要组成部分。开发一个功能完善的小程序外卖系统,需要掌握一系列关键技术和实现方法。本文将介绍小程序外卖开发中的核心技术,并提供具体的代码示例,帮助开发者理解和实…...

大数据平台之运维管理工具
大数据平台的自动化运维管理工具能够大幅提升集群管理效率,减少人为错误,提高系统的稳定性和性能。这些工具通常提供集群监控、配置管理、自动化任务执行、安全管理和故障处理等功能。以下是一些主要的大数据平台自动化运维管理工具的详细介绍࿱…...

[vue3]组件通信
自定义属性 父组件中给子组件绑定属性, 传递数据给子组件, 子组件通过props选项接收数据 props传递的数据, 在模版中可以直接使用{{ message }}, 在逻辑中使用props.message defineProps defineProps是编译器宏函数, 就是一个编译阶段的标识, 实际编译器解析时, 遇到后会进行…...
【react小项目】bmi-calculator
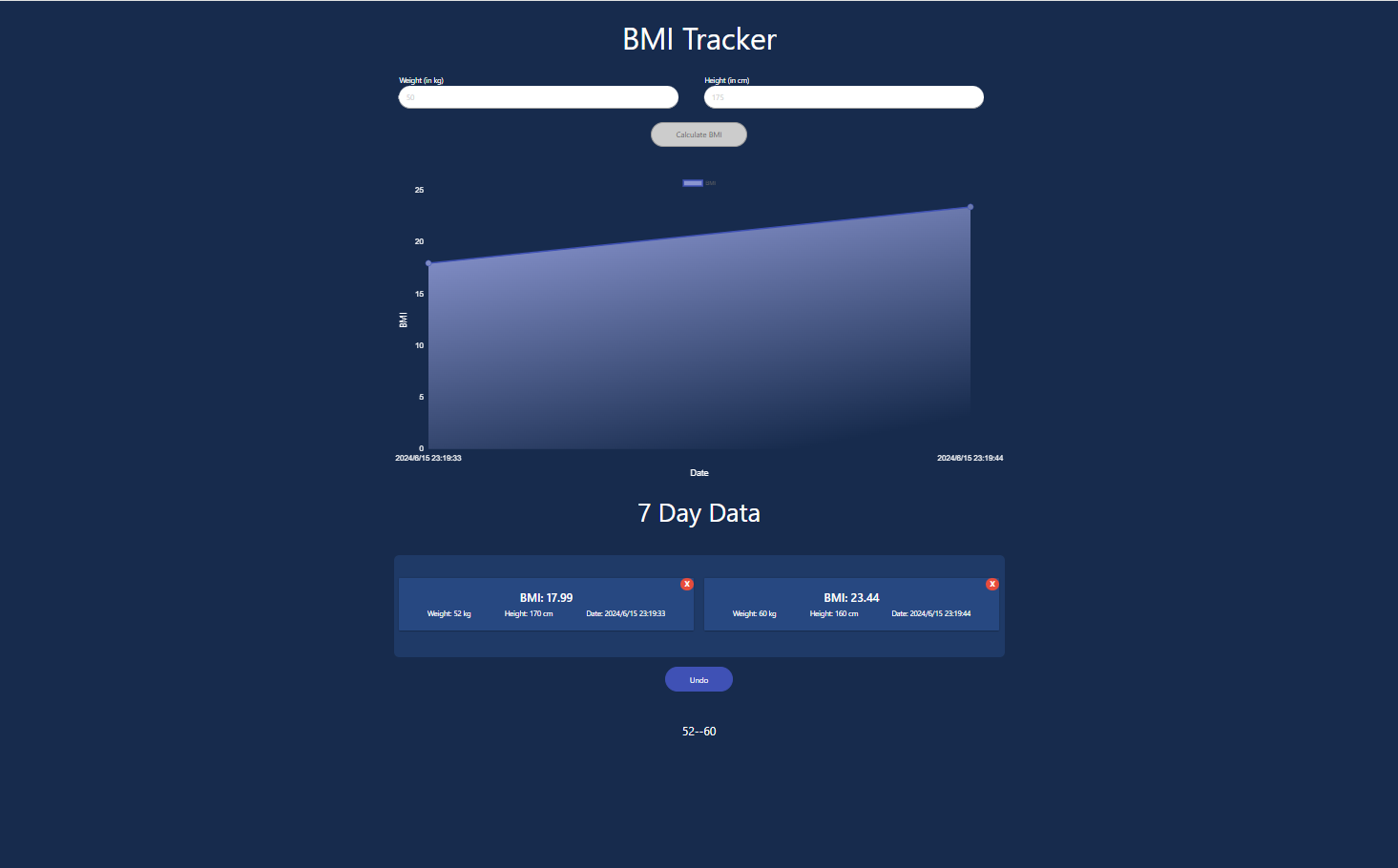
bmi-calculator 目录 bmi-calculator初始化项目01大致布局01代码 02完善样式02代码 03输入信息模块03代码 04 使用图表04代码 05详细记录信息渲染05代码 06 让数据变成响应式的06-1输入框的数据处理06-2图表,和记录信息的区域数据处理 07 删除功能,撤销功…...

python判断一个数是不是偶数
在Python中,你可以使用模运算符 % 来判断一个数是否为偶数。模运算符会返回两个数相除的余数。如果一个数除以2的余数为0,那么这个数就是偶数。 以下是一个简单的Python函数,用于判断一个数是否为偶数: def is_even(n):return n…...
Apipost模拟HTTP客户端
模拟HTTP客户端的软件有很多,其中比较著名的就有API-FOX、POSTMAN。 相信很多小伙伴都使用POSTMAN。这篇博客主要介绍Apipost的原因是,Apipost无需下载,具有网页版。 APIFOX的站内下载: Api-Fox,类似于PostMan的软件…...
uniapp 调用手机上安装的app (高德地图 百度地图 Apple地图 谷歌地图)
uniapp 调用手机上安装的app (高德地图 百度地图 Apple地图 谷歌地图) 效果 思路 获取手机类型(安卓/iOS)let platform uni.getSystemInfoSync().platform判断手机有没有安装需要的应用plus.runtime.isApplicationExist({action: ""}))打开应用 跳转过去plus.runt…...

如果供应商不能按时交货怎么办?
虽然说我们在采购的时候,我们会和供应商签订合同,合同上也会注明交期时间等一些必需的条件。 但是当供货商真的没有如期交货,或者交货拖延的时候,我们第一时间选择的是拿起法律武器来让对方承担违约责任吗? 显然,这选…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
