CCF 矩阵重塑
第一题:矩阵重塑(一)

本题有两种思路
第一种 (不确定是否正确 但是100分)
#include<iostream>
using namespace std;
int main(){int n,m,p,q,i,j;cin>>n>>m>>p>>q;int a[n][m];for(i=0;i<n;i++){for(j=0;j<m;j++){cin>>a[i][j];}}int ans=0;for(i=0;i<n;i++){for(j=0;j<m;j++){ans++;cout<<a[i][j]<<" ";if(ans%q==0){cout<<endl;}}}
} 第二种 哈希表 一对一对一(找到这两个矩阵之间的关系)
map<int,int>ok;int i,j;for(i=0;i<n;i++){for(j=0;j<m;j++){ok[i*m+j]=ans[i][j];}}for(i=0;i<p;i++){for(j=0;j<q;j++){ans[i][j]=ok[i*q+j]; }}第二题 矩阵重塑(二)

这道题他的难点在于矩阵的大小是会随着操作进行改变,所以每次需要进行更新,长和宽,这里建议用vector,因为vector独特的性质,很适合,当时我当时考试的时候就是用 数组做的(因为编译器的原因),第一天题只是作为部分功能穿插在第二题中
代码如下
#include<iostream>
#include<map>
#include<vector>
using namespace std;
int ans[10000][10000];
int n,m;
void slove1(int p,int q){map<int,int>ok;int i,j;for(i=0;i<n;i++){for(j=0;j<m;j++){ok[i*m+j]=ans[i][j];}}for(i=0;i<p;i++){for(j=0;j<q;j++){ans[i][j]=ok[i*q+j]; }}n=p;m=q;
}
void slove2(){int a[m][n];int i,j;for(i=0;i<m;i++){for(j=0;j<n;j++){a[i][j]=ans[j][i];}}for(i=0;i<m;i++){for(j=0;j<n;j++){ans[i][j]=a[i][j];}}int tmp=n;n=m;m=tmp;
}
int main(){int t,i,j;cin>>n>>m>>t;for(i=0;i<n;i++){for(j=0;j<m;j++){cin>>ans[i][j];}}int op,p,q;while(t--){cin>>op>>p>>q;if(op==1){slove1(p,q);}if(op==2){slove2();}if(op==3){cout<<ans[p][q]<<endl;}}
} 可以把slove1()修改成如下
void slove1(int p,int q){int i,j;int nums[n][m];for(i=0;i<n;i++){for(j=0;j<m;j++){nums[i][j]=ans[i][j];}}for(i=0;i<n*m;i++){ans[i/p][i%q]=nums[i/n][i%n];}n=p;m=q;
}可以参考leetcode
以上只能得80分
566. 重塑矩阵 - 力扣(LeetCode)
相关文章:

CCF 矩阵重塑
第一题:矩阵重塑(一) 本题有两种思路 第一种 (不确定是否正确 但是100分) #include<iostream> using namespace std; int main(){int n,m,p,q,i,j;cin>>n>>m>>p>>q;int a[n][m];for(i…...

Aigtek高压放大器在柔性爬行机器人驱动性能研究中的应用
实验名称:柔性爬行机器人的材料测试 研究方向:介电弹性体的最小能量结构是一种利用DE材料的电致变形与柔性框架形变相结合设计的新型柔性驱动器,所谓最小能量是指驱动器在平衡状态时整个系统的能量最小,当系统在外界的电压刺激下就…...

Postman下发流表至Opendaylight
目录 任务目的 任务内容 实验原理 实验环境 实验过程 1、打开ODL控制器 2、网页端打开ODL控制页面 3、创建拓扑 4、Postman中查看交换机的信息 5、L2层流表下发 6、L3层流表下发 7、L4层流表下发 任务目的 1、掌握OpenFlow流表相关知识,理解SDN网络中L…...

C语言王国——数组的旋转(轮转数组)三种解法
目录 一、题目 二、分析 2.1 暴力求解法 2.2 找规律 2.3 追求时间效率,以空间换时间 三、结论 一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出…...

MySQL中CAST和CONVERT函数都用于数据类型转换
在 MySQL 中,CAST() 和 CONVERT() 函数都用于数据类型转换。虽然这两个函数在大多数情况下可以互换使用,但它们之间还是有一些细微的差别。 官方文档地址 https://dev.mysql.com/doc/refman/8.4/en/cast-functions.html#function_cast CAST() 函数 C…...

速盾:cdn影响seo吗?
CDN (Content Delivery Network) 是一个分布式网络架构,用于在全球范围内加速网站内容的传输和分发。它通过将网站的静态资源(例如图片、CSS、JavaScript 文件等)存储在多个服务器上,使用户可以从最接近他们位置的服务器上获取这些…...
期末算法复习
0-1背包问题(动态规划) 例题 算法思想: 动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。 主要是状态转移方程和状态 算法描述: 初始化一个二维数组dp࿰…...

可穿戴设备:苹果“吃老底”、华为“忙复苏”、小米“再扩容”
配图来自Canva可画 随着产品功能的创新,可穿戴设备不再被简单地视为手机的延伸,而是被当成一种独立的、具有独特功能和优势的产品,受到了越来越多人的青睐。 一方面,技术的进步使得可穿戴设备在功能、性能和使用体验上得到显著提…...

AI数据分析:集中度分析和离散度分析
在deepseek中输入提示词: 你是一个Python编程专家,要完成一个Python脚本编写的任务,具体步骤如下: 读取Excel表格:"F:\AI自媒体内容\AI行业数据分析\toolify月榜\toolify2023年-2024年月排行榜汇总数据.xlsx&qu…...

redis的分布式session和本地的session有啥区别
在web应用开发中,Session用于在多个请求之间存储用户数据。传统上,Session存储在服务器的内存中,即本地Session。然而,随着应用规模和复杂度的增加,特别是在分布式环境中,本地Session会遇到一些问题。这时&…...

SSH概念、用途、详细使用方法
还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas,webgl,ech…...
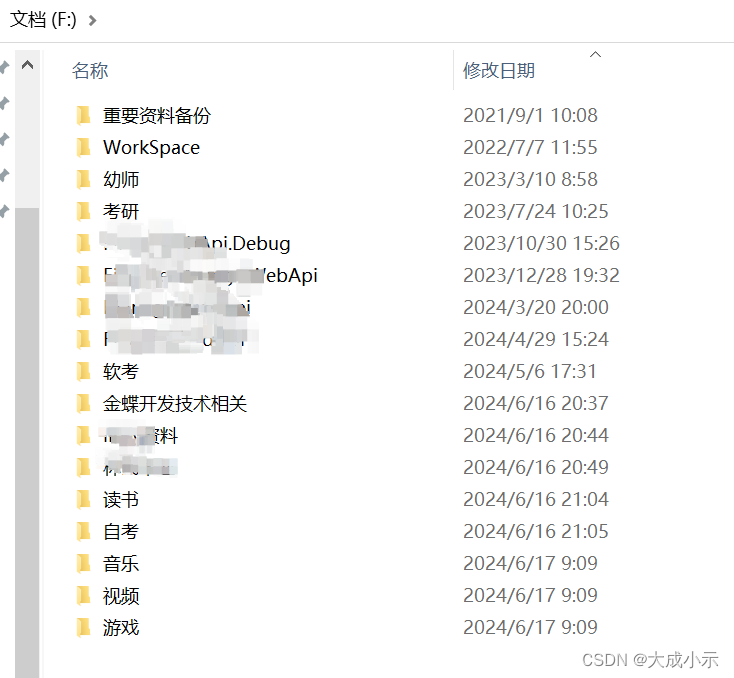
关于电脑文件的规划思考
概述 设置C、D、E、F 四个盘 C盘:系统数据使用,操作系统、其他软件需要用到的系统性资源 D盘:应用软件区 的使用,数据库、navacat、idea、visual studio、浏览器、向日葵、虚拟机…… E盘:工作区:公司资料…...
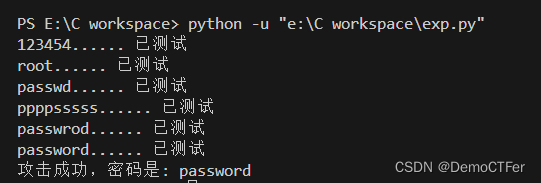
DVWA - Brute Force
DVWA - Brute Force 等级:low 直接上bp弱口令爆破,设置变量,攻击类型最后一个,payload为用户名、密码简单列表 直接run,长度排序下,不一样的就是正确的用户名和密码 另解: 看一下…...
安卓手机文件找回方法汇总,3个技巧,不再焦虑
我们用手机来储存各种重要的信息和文件,无论是珍贵的照片、重要的文档还是喜爱的音乐,用来记录和分享生活中的每一个瞬间。但如果不小心删除了这些文件,我们可能会面临数据丢失的风险,进而产生焦虑和不安。本文将为您揭秘手机文件…...

{}初始化
文章目录 ()初始化的问题易混淆弱检查 {}初始化{}初始化是c11推荐的初始化,解决了上述的问题 ()则被用于强制类型转换 ()初始化的问题 易混淆 string s();不能确定是函数定义还是对象定义 弱检查 int a(3.14);3.14 可以通过 int 定义 {}初始化 {}初始化是c11推…...

小程序外卖开发中的关键技术与实现方法
小程序外卖服务凭借其便捷性和灵活性,正成为现代餐饮行业的重要组成部分。开发一个功能完善的小程序外卖系统,需要掌握一系列关键技术和实现方法。本文将介绍小程序外卖开发中的核心技术,并提供具体的代码示例,帮助开发者理解和实…...

大数据平台之运维管理工具
大数据平台的自动化运维管理工具能够大幅提升集群管理效率,减少人为错误,提高系统的稳定性和性能。这些工具通常提供集群监控、配置管理、自动化任务执行、安全管理和故障处理等功能。以下是一些主要的大数据平台自动化运维管理工具的详细介绍࿱…...

[vue3]组件通信
自定义属性 父组件中给子组件绑定属性, 传递数据给子组件, 子组件通过props选项接收数据 props传递的数据, 在模版中可以直接使用{{ message }}, 在逻辑中使用props.message defineProps defineProps是编译器宏函数, 就是一个编译阶段的标识, 实际编译器解析时, 遇到后会进行…...
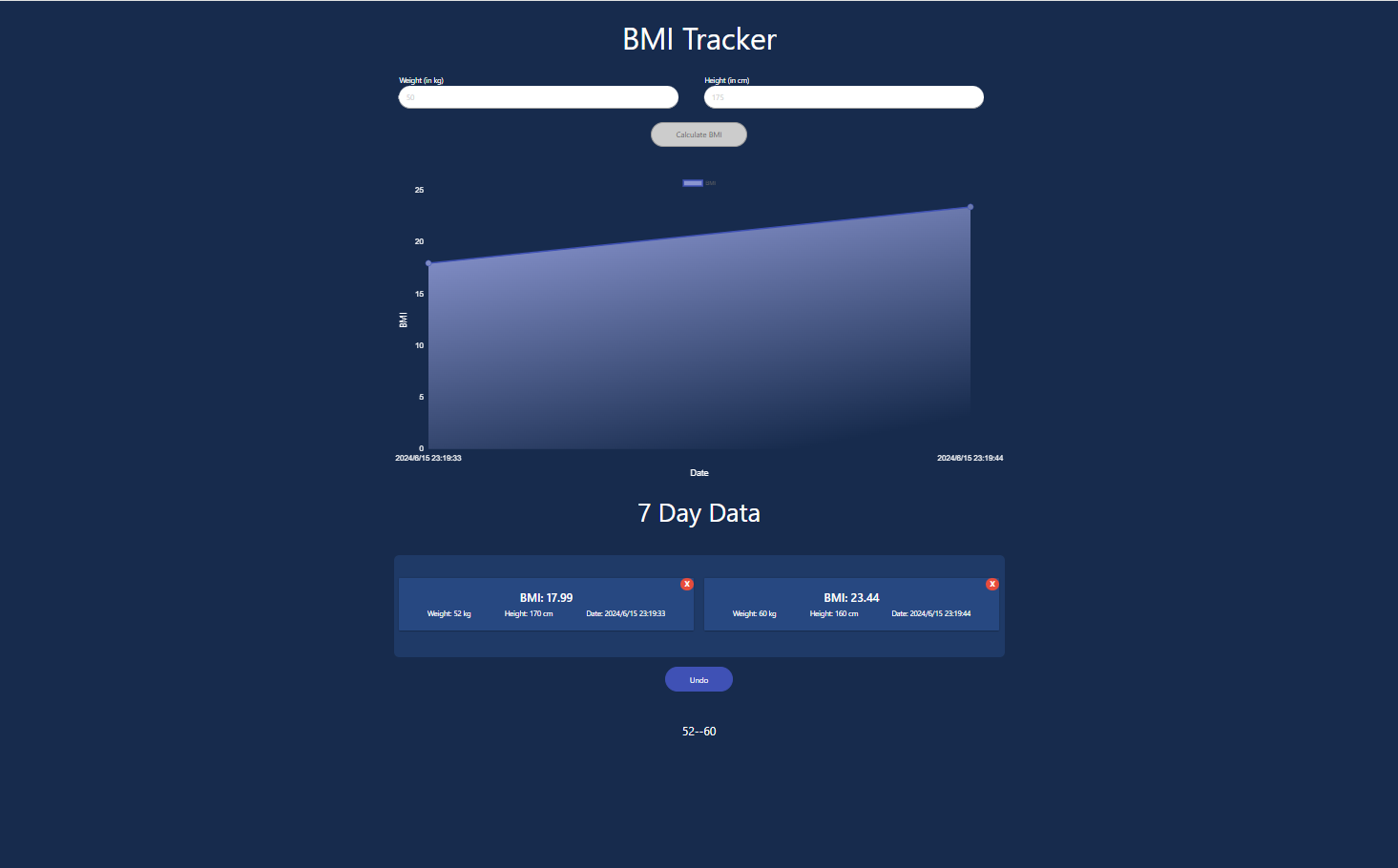
【react小项目】bmi-calculator
bmi-calculator 目录 bmi-calculator初始化项目01大致布局01代码 02完善样式02代码 03输入信息模块03代码 04 使用图表04代码 05详细记录信息渲染05代码 06 让数据变成响应式的06-1输入框的数据处理06-2图表,和记录信息的区域数据处理 07 删除功能,撤销功…...

python判断一个数是不是偶数
在Python中,你可以使用模运算符 % 来判断一个数是否为偶数。模运算符会返回两个数相除的余数。如果一个数除以2的余数为0,那么这个数就是偶数。 以下是一个简单的Python函数,用于判断一个数是否为偶数: def is_even(n):return n…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
