如何挑到高质量的静态IP代理?

在数字化时代,静态住宅IP代理已成为网络活动中不可或缺的一部分。无论是数据采集、网站访问,还是其他需要隐藏真实IP地址的在线活动,高质量的静态住宅IP代理都发挥着至关重要的作用。今天IPIDEA代理IP将详细介绍如何获取高质量的静态住宅IP代理,以满足您在网络活动中的需求。
首先,我们要明确什么是静态住宅IP代理。静态住宅IP代理是来自真实住宅网络的IP地址,这些IP地址由国际ISP供应商分配给家庭和个人用户。因此,它们具有较高的真实性和稳定性,能够在长时间内持续提供服务,在连接稳定性和可靠性方面更具优势。
接着我们来看获取高质量静态住宅IP代理的几种途径:
一、专业代理商
选择专业的IP代理服务商,这些服务商通常拥有大量的静态住宅IP资源,能够满足不同用户的需求。同时,他们还提供多种灵活的购买方式,方便用户根据需求选择合适的套餐。在选择代理服务商时,请确保选择具有良好声誉和可靠性的公司,以保证服务质量。
二、利用开源资源
互联网上还存在一些开源的IP代理资源,这些资源可能包含静态住宅IP地址。然而,需要注意的是,这些资源的真实性和稳定性往往难以保证。因此,在使用这些资源时,请务必进行充分的测试和验证,以确保其满足您的需求。
三、自建代理服务器
如果您具备一定的技术知识和设备支持,也可以尝试自建代理服务器来获取静态住宅IP代理。这需要您了解代理服务器的原理和技术,以及如何从住宅网络中获取IP地址。虽然自建代理服务器具有较高的灵活性和可定制性,但也需要投入较多的时间和精力。

在获取高质量的静态住宅IP代理时,还需要注意以下几点:
1. 验证IP地址的真实性:确保获取的IP地址来自真实的住宅网络,而非数据中心或其他非住宅环境。这可以通过查询IP地址的地理位置、ISP信息等方式进行验证。
2. 关注稳定性和可靠性:静态住宅IP代理需要具有较高的稳定性和可靠性,以确保在网络活动中能够持续提供服务。因此,在选择代理时,务必关注稳定性和可靠性方面的表现。
3. 遵守法律法规:在获取和使用静态住宅IP代理时,请确保遵守当地的法律法规。未经授权擅自使用他人的IP地址可能涉及违法行为,请务必避免。
相关文章:

如何挑到高质量的静态IP代理?
在数字化时代,静态住宅IP代理已成为网络活动中不可或缺的一部分。无论是数据采集、网站访问,还是其他需要隐藏真实IP地址的在线活动,高质量的静态住宅IP代理都发挥着至关重要的作用。今天IPIDEA代理IP将详细介绍如何获取高质量的静态住宅IP代…...
vagrant putty错误的解决
使用Vagrant projects for Oracle products and other examples 新创建的虚机,例如vagrant-projects/OracleLinux/8。 用vagrant ssh可以登录: $ vagrant ssh > vagrant: Getting Proxy Configuration from Host...Welcome to Oracle Linux Server …...
图像分割——U-Net论文介绍+代码(PyTorch)
0、概要 原理大致介绍了一下,后续会不断精进改的更加详细,然后就是代码可以对自己的数据集进行一个训练,还会不断完善,相应其他代码可以私信我。 一、论文内容总结 摘要:人们普遍认为,深度网络成功需要数…...
C#进阶-ASP.NET的WebService跨域CORS问题解决方案
在现代的Web应用程序开发中,跨域资源共享(Cross-Origin Resource Sharing, CORS)问题是开发者经常遇到的一个挑战。特别是当前端和后端服务部署在不同的域名或端口时,CORS问题就会显得尤为突出。在这篇博客中,我们将深…...

如何利用TikTok矩阵源码实现自动定时发布和高效多账号管理
在如今社交媒体的盛行下,TikTok已成为全球范围内最受欢迎的短视频平台之一。对于那些希望提高效率的内容创作者而言,手动发布和管理多个TikTok账号可能会是一项繁琐且耗时的任务。幸运的是,通过利用TikTok矩阵源码,我们可以实现自…...

Java高级编程技术详解:从多线程到算法优化的全面指南
复杂度与优化 复杂度与优化在算法中的应用 算法复杂度是衡量算法效率的重要指标。了解和优化算法复杂度对提升程序性能非常关键。本文将介绍时间复杂度和空间复杂度的基本概念,并探讨一些优化技术。 时间复杂度和空间复杂度 时间复杂度表示算法执行所需时间随输…...

Redis 分布式锁过期了,还没处理完怎么办?
为了防止死锁,我们会给分布式锁加一个过期时间,但是万一这个时间到了,我们业务逻辑还没处理完,怎么办? 这是一个分布式应用里很常见到的需求,关于这个问题,有经验的程序员会怎么处理呢ÿ…...

Vue2+Element-ui后台系统常用js方法
el-dialog弹框关闭清空form表单并清空验证 cancelDialog(diaLog, formRef) {this[diaLog] falseif (formRef) {this.$refs[formRef].resetFields()} }页面使用: <el-dialog :visible.sync"addSubsidyDialog.dialog" close"cancelDialog(addSub…...

Kafka高频面试题整理
文章目录 1、什么是Kafka?2、kafka基本概念3、工作流程4、Kafka的数据模型与消息存储机制1)索引文件2)数据文件 5、ACKS 机制6、生产者重试机制:7、kafka是pull还是push8、kafka高性能高吞吐的原因1)磁盘顺序读写:保证了消息的堆积2)零拷贝机…...

uniapp地图自定义文字和图标
这是我的结构: <map classmap id"map" :latitude"latitude" :longitude"longitude" markertap"handleMarkerClick" :show-location"true" :markers"covers" /> 记住别忘了在data中定义变量…...

k8s_探针专题
关于探针 生产环境中一定要给pod设置探针,不然pod内的应用发生异常时,K8s将不会重启pod。 需要遵循以下几个原则(本人自己总结,仅供参考): 探针尽量简单,不要消耗过多资源。因为探针较为频繁的…...

MySQL触发器基本结构
1、修改分隔符符号 delimiter $$ 可以修改成$$ //都行 2、创建触发器函数名称 create trigger 函数名 3、什么样的操作出发,操作那个表 after:......之后触发 befor:......之前触发 insert:插入被触发 update:修改被触…...

前缀和(一维前缀和+二维前缀和)
前缀和 定义: 前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。 用途: 前缀和一般用于统计一个区间的和&…...

web前端五行属性:深入探索与实战解析
web前端五行属性:深入探索与实战解析 在Web前端开发中,五行属性这一概念或许听起来有些陌生。然而,如果我们将其与前端开发的核心理念相结合,就能发现其中蕴含的深刻内涵。本文将从四个方面、五个方面、六个方面和七个方面&#…...

白酒:茅台镇白酒的酒厂社会责任与可持续发展
云仓酒庄豪迈白酒,作为茅台镇的品牌,不仅在产品品质和口感方面有着卓着的表现,在酒厂社会责任和可持续发展方面也做出了积极的探索和实践。 首先,云仓酒庄豪迈白酒注重环境保护和资源利用。酒厂在生产过程中严格控制能源消耗和排放…...

音视频开发_SDL音频播放器的实现
今天向大家介绍一下如何通过 SDL 实现一个PCM音频播放器。这是一个最简单的播放器,它不涉及到音频的解复用,解码等工作。我们只需要将音频原始数据喂给 SDL 音频接口就可以听到悦耳的声音了。在下面的列子中我将向你演示,使用 SDL 做这样一个…...
C语言学习系列:初识C语言
前言,C语言是什么 语言,比如中文、英语、法语、德语等,是人与人交流的工具。 C语言也是语言,不过是一种特殊的语言,是人与计算机交流的工具。 为什么叫C语言呢? 这就要从C语言的历史说起了。 一&#…...
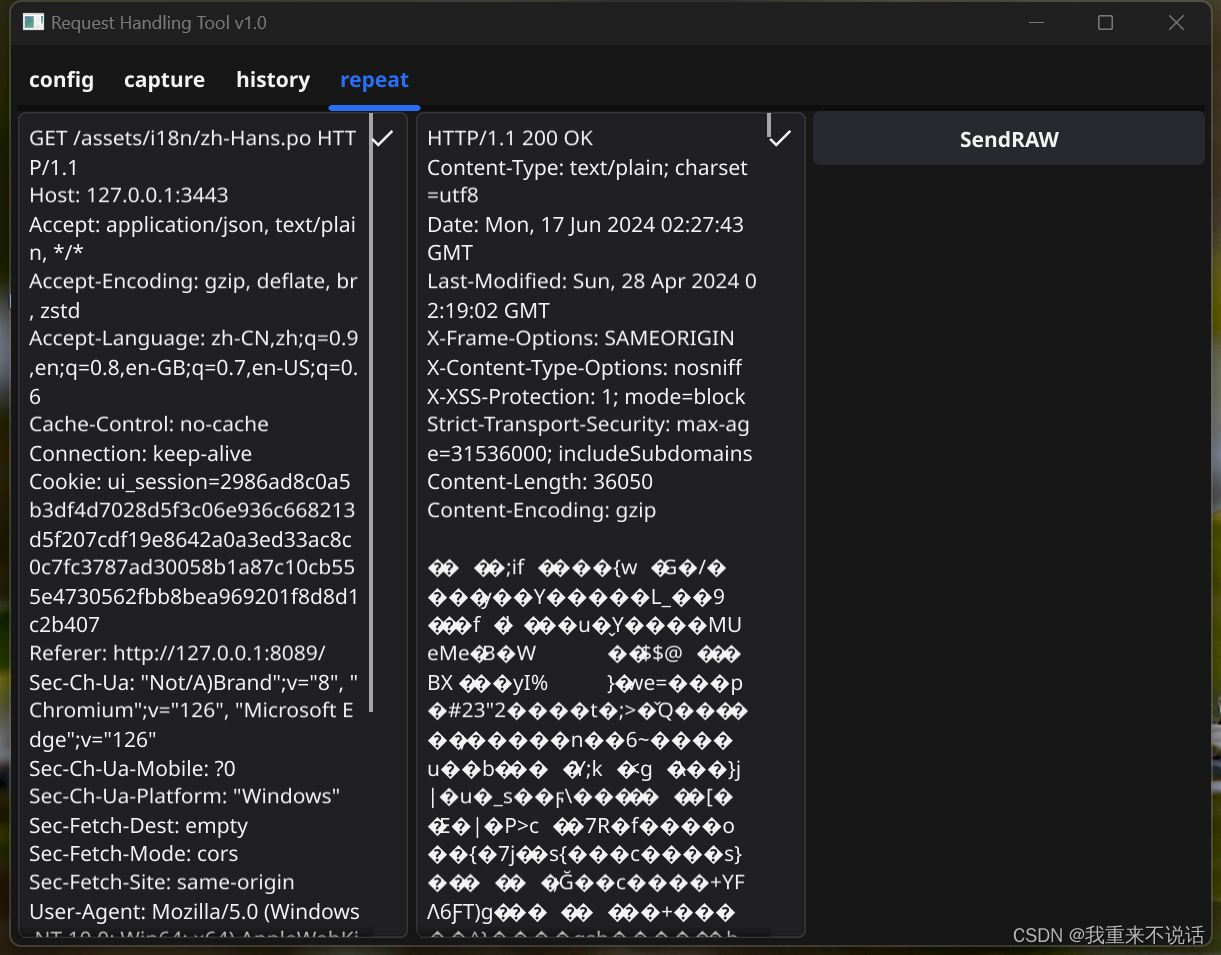
利用反向代理编写HTTP抓包工具——可视化界面
手写HTTP抓包工具——可视化界面 项目描述语言golang可视化fynev2功能代理抓包、重发、记录 目录 1. 示例1.1 主界面1.2 开启反向代理1.3 抓包1.4 历史记录1.5 重发 2. 核心代码2.1 GUI2.1 抓包 3. 结语3.1 传送门 1. 示例 1.1 主界面 1.2 开启反向代理 1.3 抓包 1.4 历史记录…...

下拉框数据被遮挡 且 后续数据无法下拉的 解决方法
目录 前言1. 问题所示2. 原理分析3. 解决方法3.1 添加空白版2.2 调整z-index2.3 父容器的溢出属性2.4 调整样式属性4. 效果图前言 小程序使用的是Uniapp,原理都差不多,索性标题就不标注Uniapp(小程序) 对于该问题调试了一个晚上,最终解决,对此记录下来 1. 问题所示 执…...

课设--学生成绩管理系统(二)
欢迎来到 Papicatch的博客 目录 🐋引言 🦈编写目的 🦈项目说明 🐋产品介绍 🦈产品概要说明 🦈产品用户定位 🦈产品中的角色 🐋 产品总体业务流程图 🐋 产品功…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
