归并排序个人见解
归并排序个人见解
- 思路实现
- 代码实现
- 题目
思路实现
归并排序属于分治算法,分治算法有三个步骤:
- 分:将问题划分为多个规模较小的子问题,这些子问题与原始问题相似。
- 治:递归地解决这些子问题。如果子问题足够小,可以直接求解。
- 合:将子问题的解合并为原始问题的解。
归并排序的重点主要是 合,合 的过程中就会直接排好序。(这里是从小到大排序)
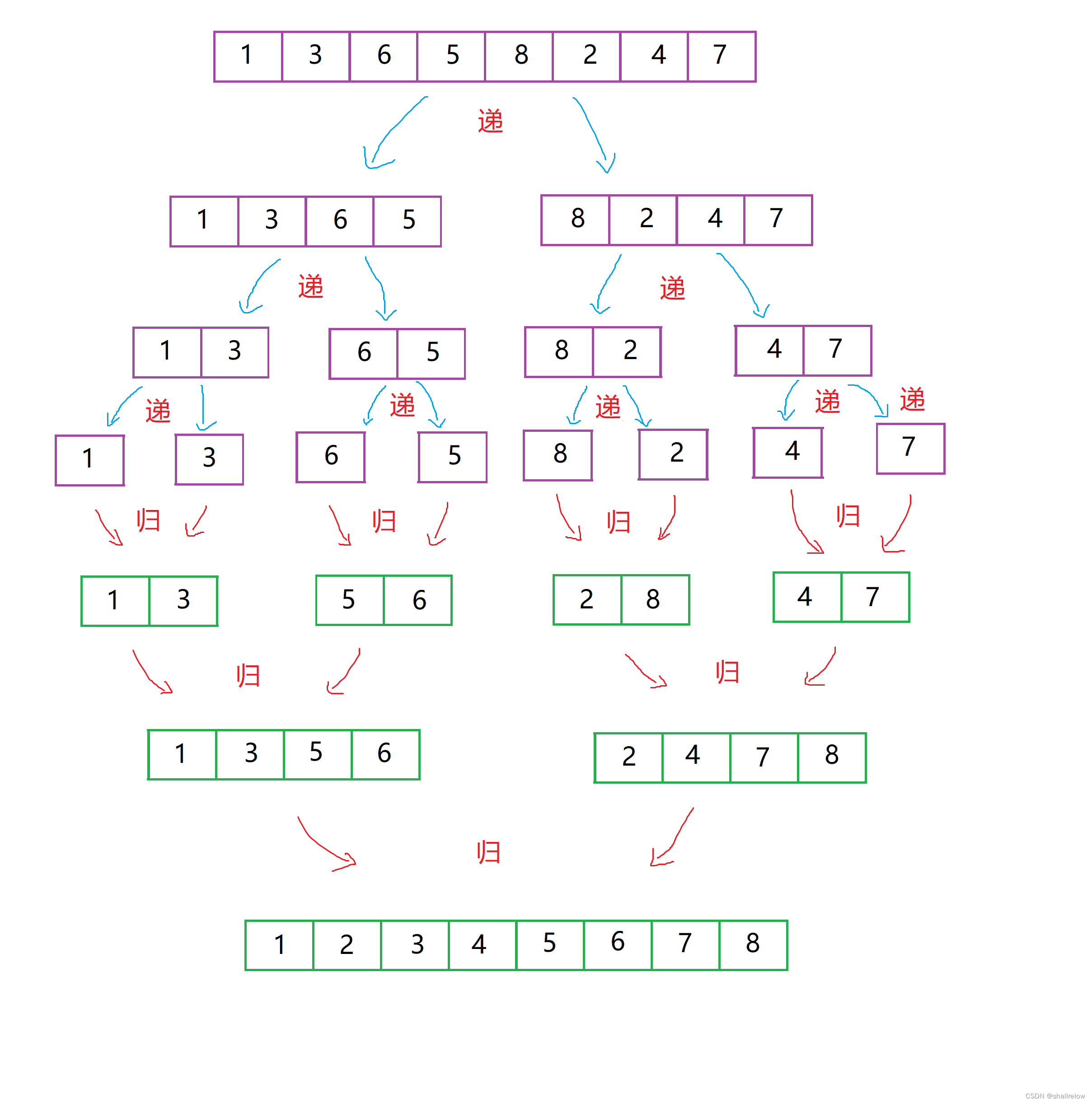
我们来模拟一下合的过程。
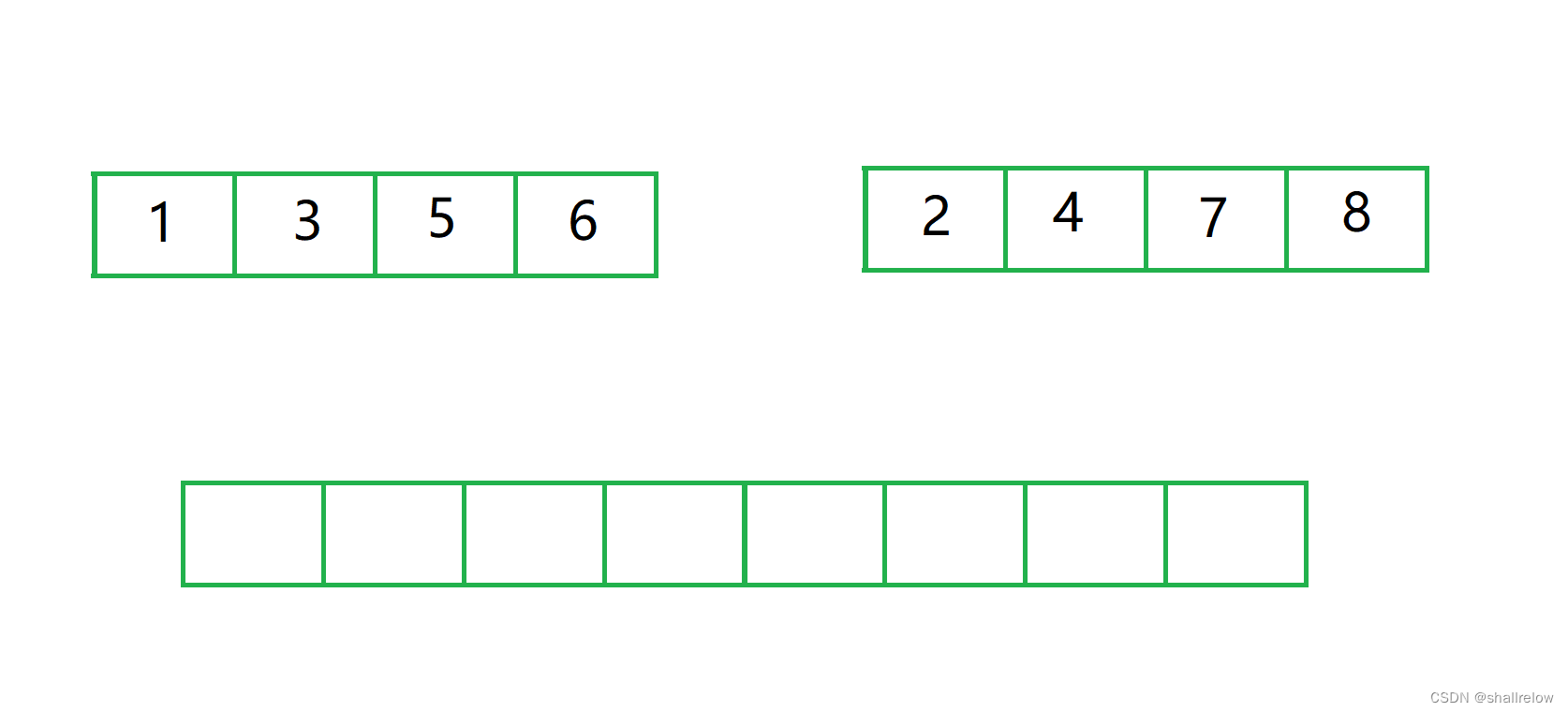
首先合的两个序列,一定都已经是有序的了。(如果不理解这个“一定有序” 后面会说的,先理解怎么合并的)
在合的过程中,有一块临时数组,也就是图中这个空的空间。
此时需要三个下标,分别指向两个序列的头和 那份空的空间的头。
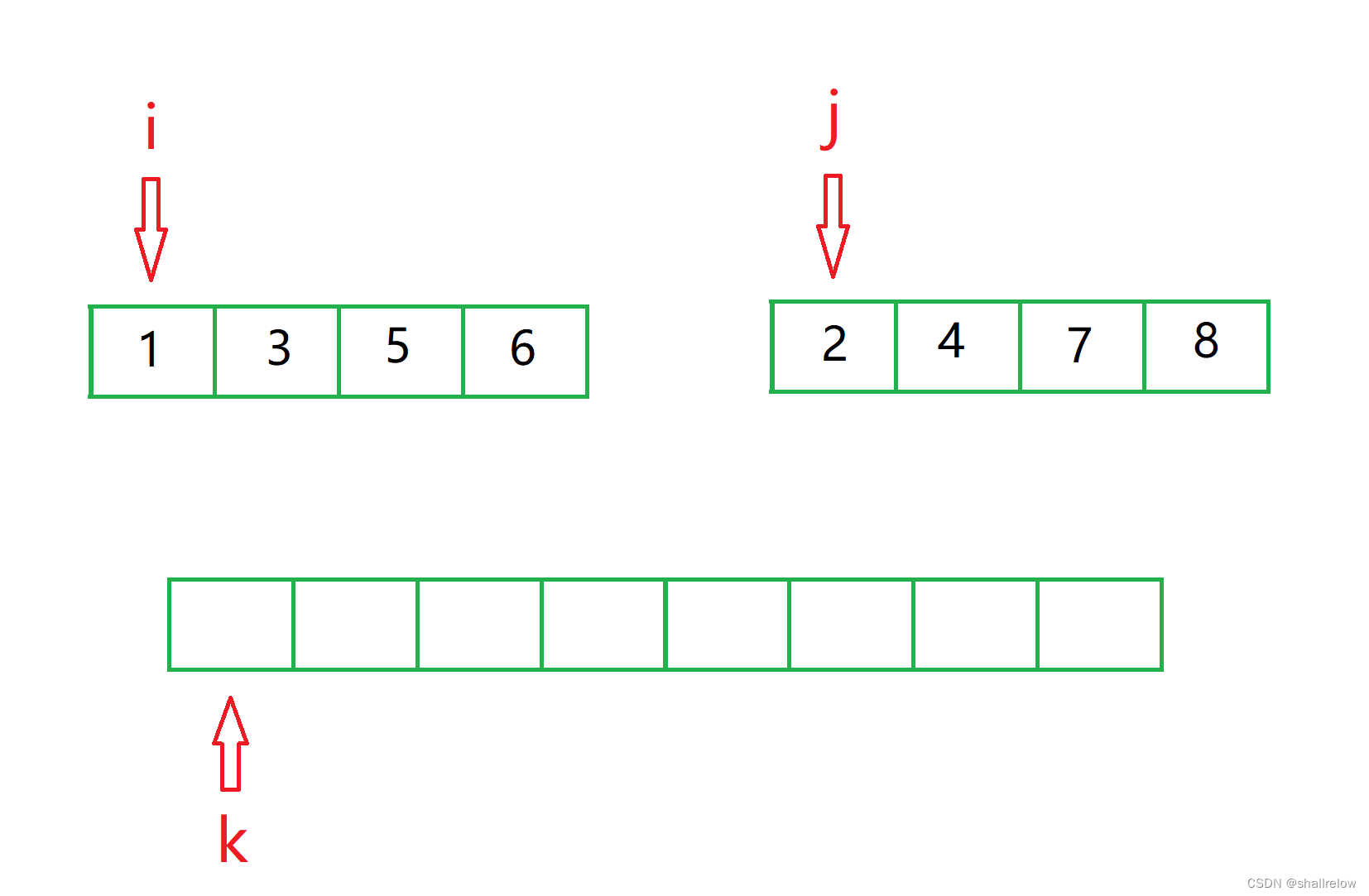
此时比较 下标 i 和 j 的 值,小的那个 赋给 临时空间的 k 坐标,然后 小的坐标 和 k 都自增1。
对于图中的情况,那么就是1 过去。

然后继续比较 下标 为 i 的值和 下标为 j 的值。
此时 j 小,所以 2 过去。

然后一直重复此效果,此时必定有一个序列先把自己的数字 放完了。
比如图中的情况。
最终 下标 i 会移动到序列的外部(当然其实他是指向了右边的那个2,因为这两个序列其实是连续的)
所以此时不能够再次比较了。
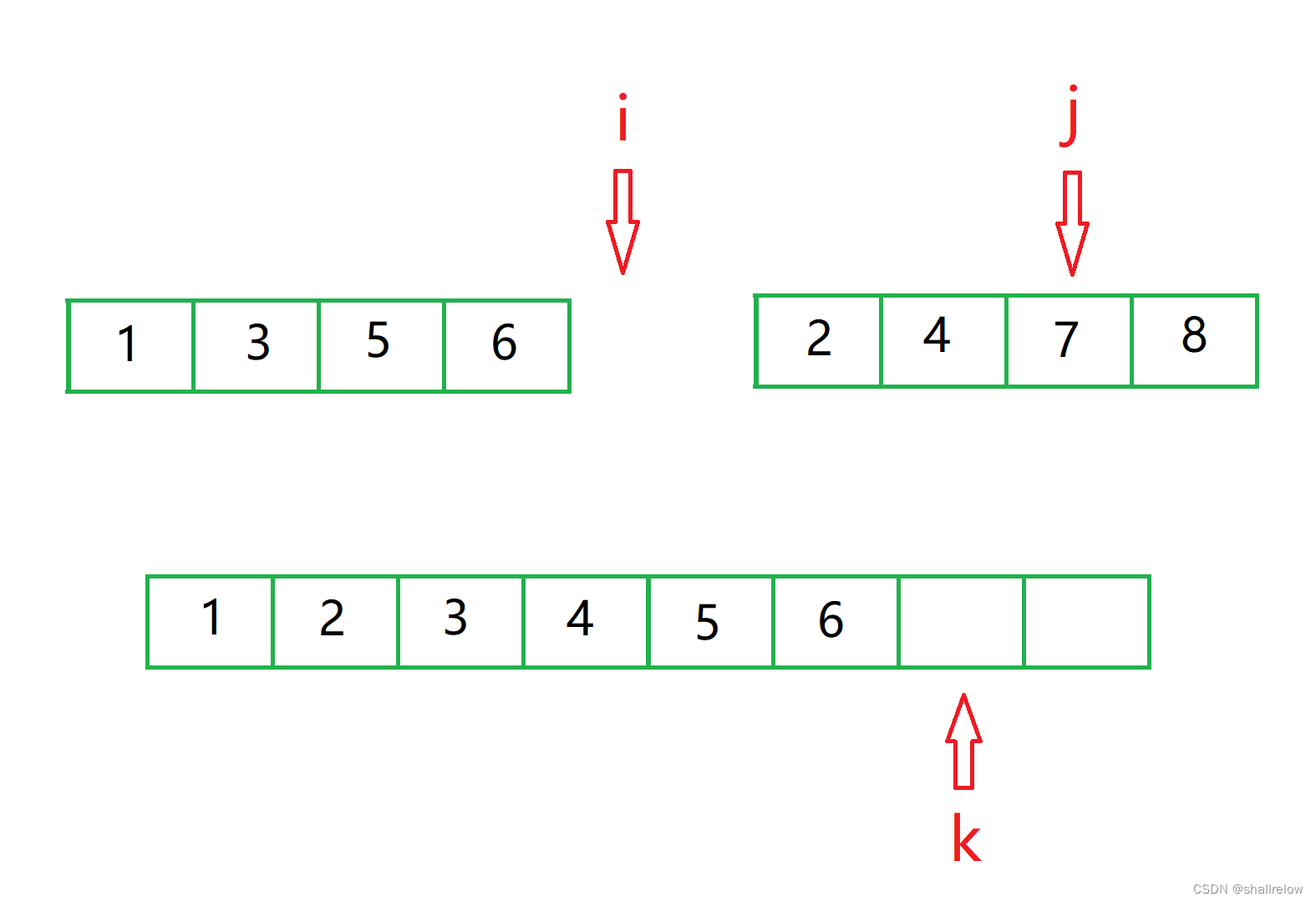
接下来我们就需要判断 i 和 j 谁是否在序列内,谁在序列内,就循环的将值放到数组内。
比如这时 只有 j 在序列内部,所以就循环的将值放到临时数组里面,直到 j 出去了。

此时就会发现数组 排序好了。
而为什么两个序列一定是有序的是因为 归并排序会使用递归,会先递到只有一个元素。
比如刚才的那个图

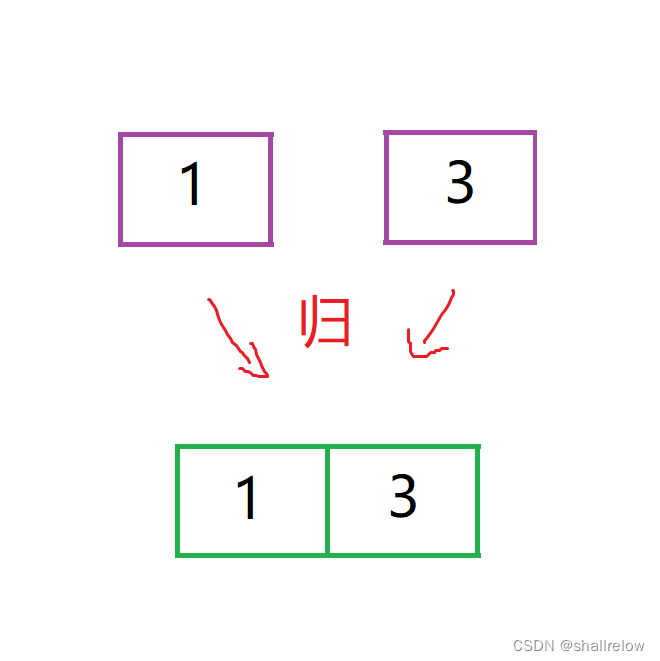
在递到 只有一个元素的时候,它一定是有序的,因为只有一个数字啊。
所以往下合并的时候就一定是 有序的。
代码实现
接下来我们来看看代码,看完代码你就会恍然大悟了,如果没有,那么你可以再次看一下前面的思路。
我们以题目为引入。
题目
给定你一个长度为 n n n 的整数数列。
请你使用归并排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n n n。
第二行包含 n n n 个整数(所有整数均在 1 ∼ 1 0 9 1 \sim 10^9 1∼109 范围内),表示整个数列。
输出格式
输出共一行,包含 n n n 个整数,表示排好序的数列。
数据范围
1 ≤ n ≤ 100000 1 \le n \le 100000 1≤n≤100000
输入样例:
5
3 1 2 4 5
输出样例:
1 2 3 4 5
首先是准备阶段:

其中 题目当中 n 最大为 10的五次方,所以开辟这么大的数组。
这个tem为临时数组。
接着输入环节:

然后把归并排序封装成一个函数,最后直接输出。

对于归并排序函数来说,参数是 要排序的数组 和 要排序的区间头和区间尾。

还记得刚才的分治算法的三个步骤吗?
分、治、合。
首先是分,将问题分为多个子问题。
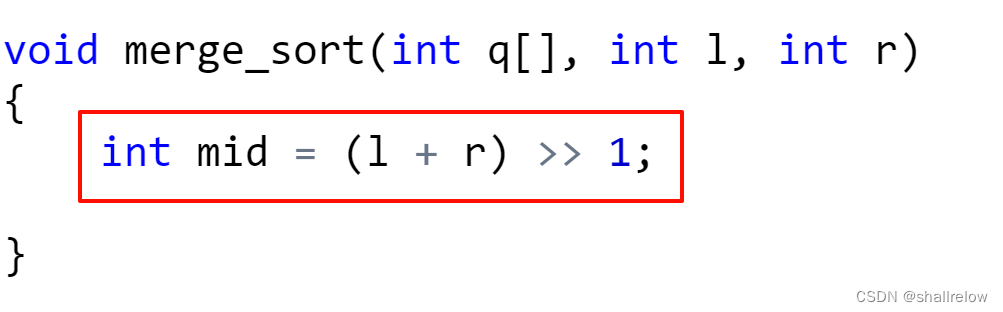
然后是治,递归处理子问题。

一想到递归,你就必须要考虑递归的结束条件,不能说让递归一直递下去。
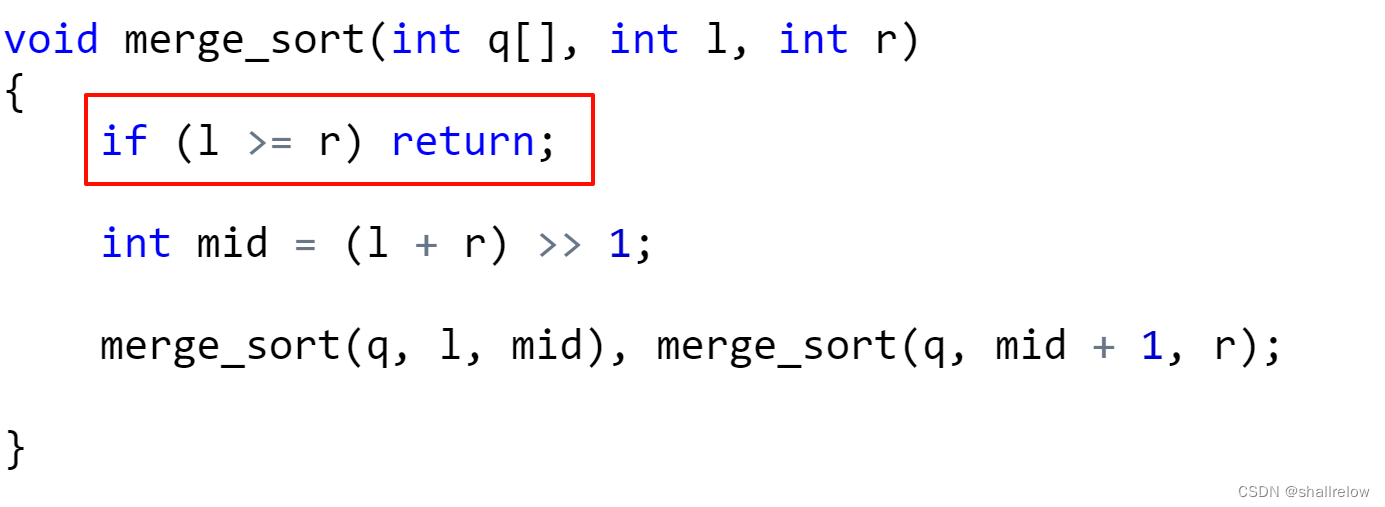
所以我们需要在开头加上此语句。
这句话的意思,如果此时区间内没有元素或只有一个元素,就不需要往下递了。
分 和 治都完了,那么接下来就是 合 了。
还记得刚才的思路吗,首先我们需要创建三个坐标。

其中 下标 i 是 区间 [ l, mid ] 的头,下标 j 是 区间 [ mid+1, r ] 的头,k是 临时数组 tem 的头。
[ l, mid ] 和 [ mid+1, r ] 这两个区间也跟我们上边的递归的区间是一致的。
创建完之后,接下来就是循环比较 i 和 j 的值了。
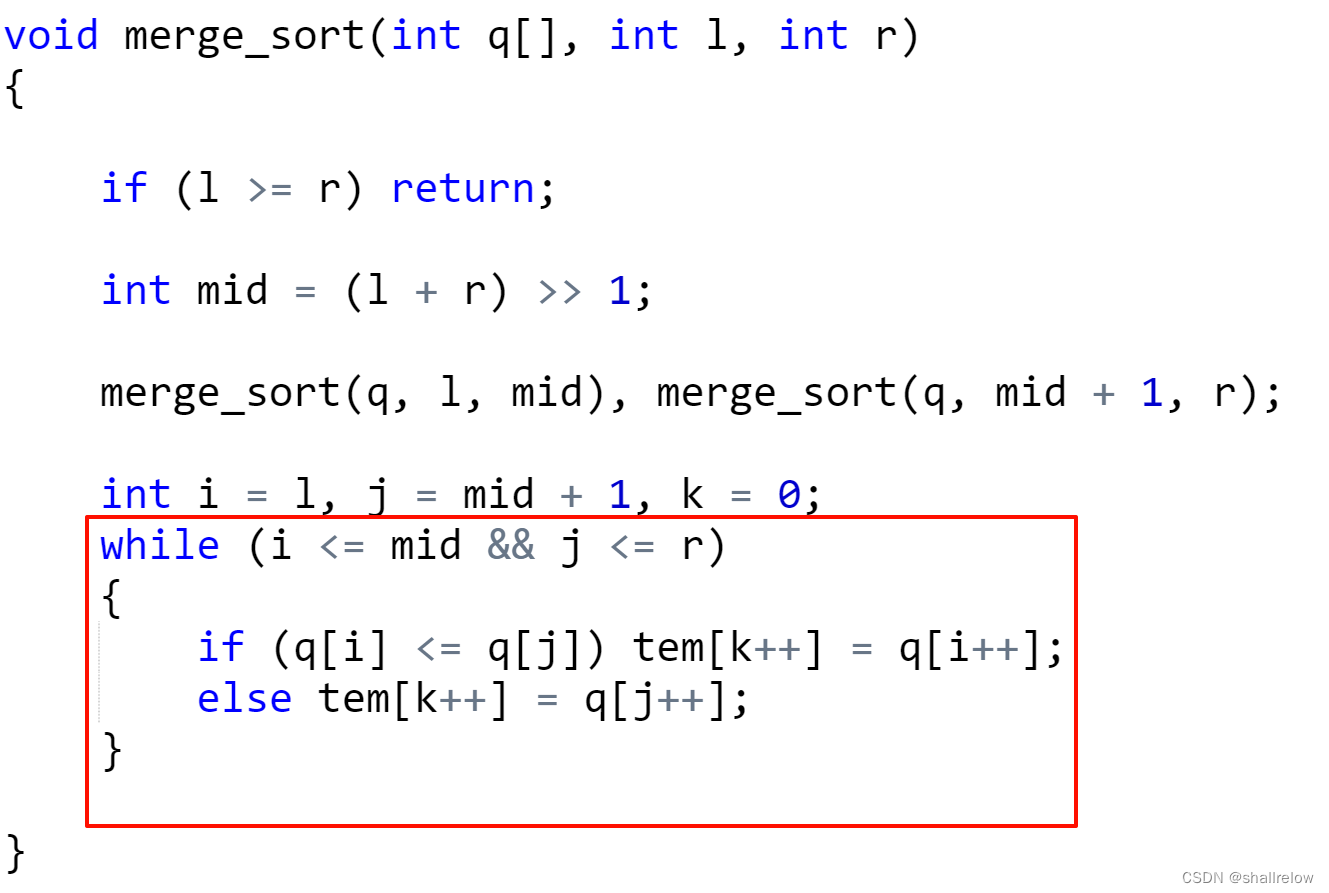
循环直到 i 或者 j 的一个 跳出它的区间 后终止。
接着就需要 让还在 区间内部的 i 或者 j 走完整个区间。

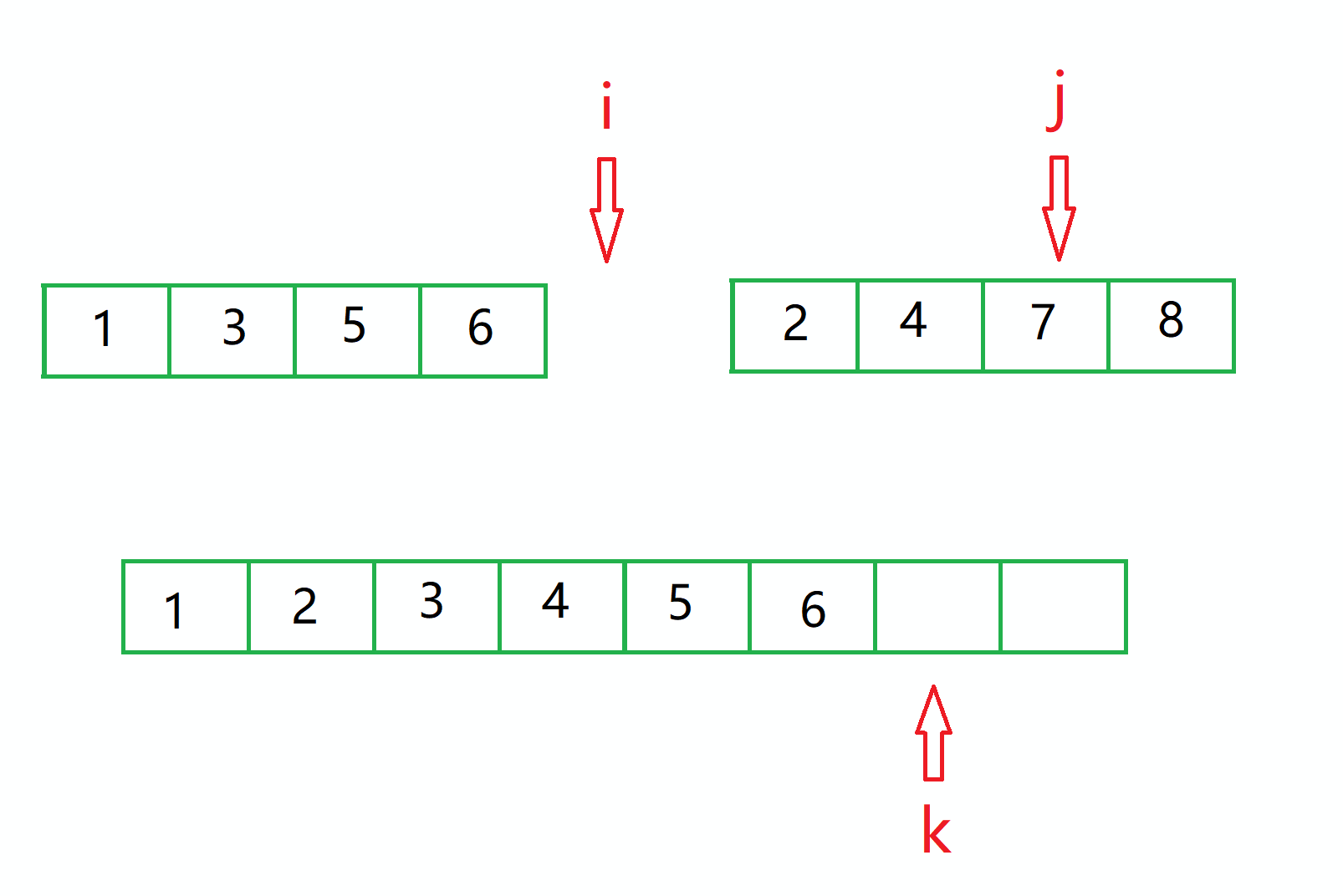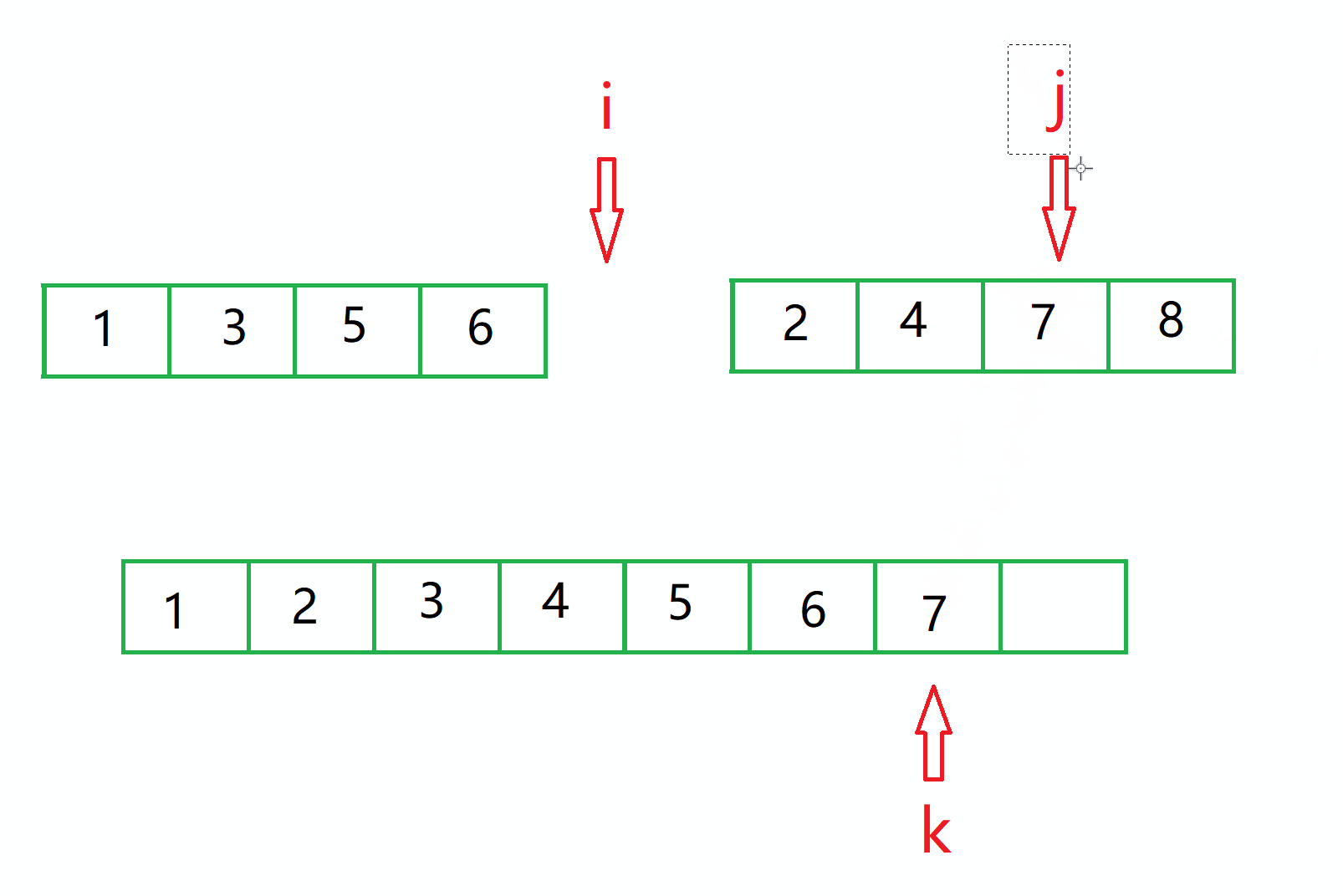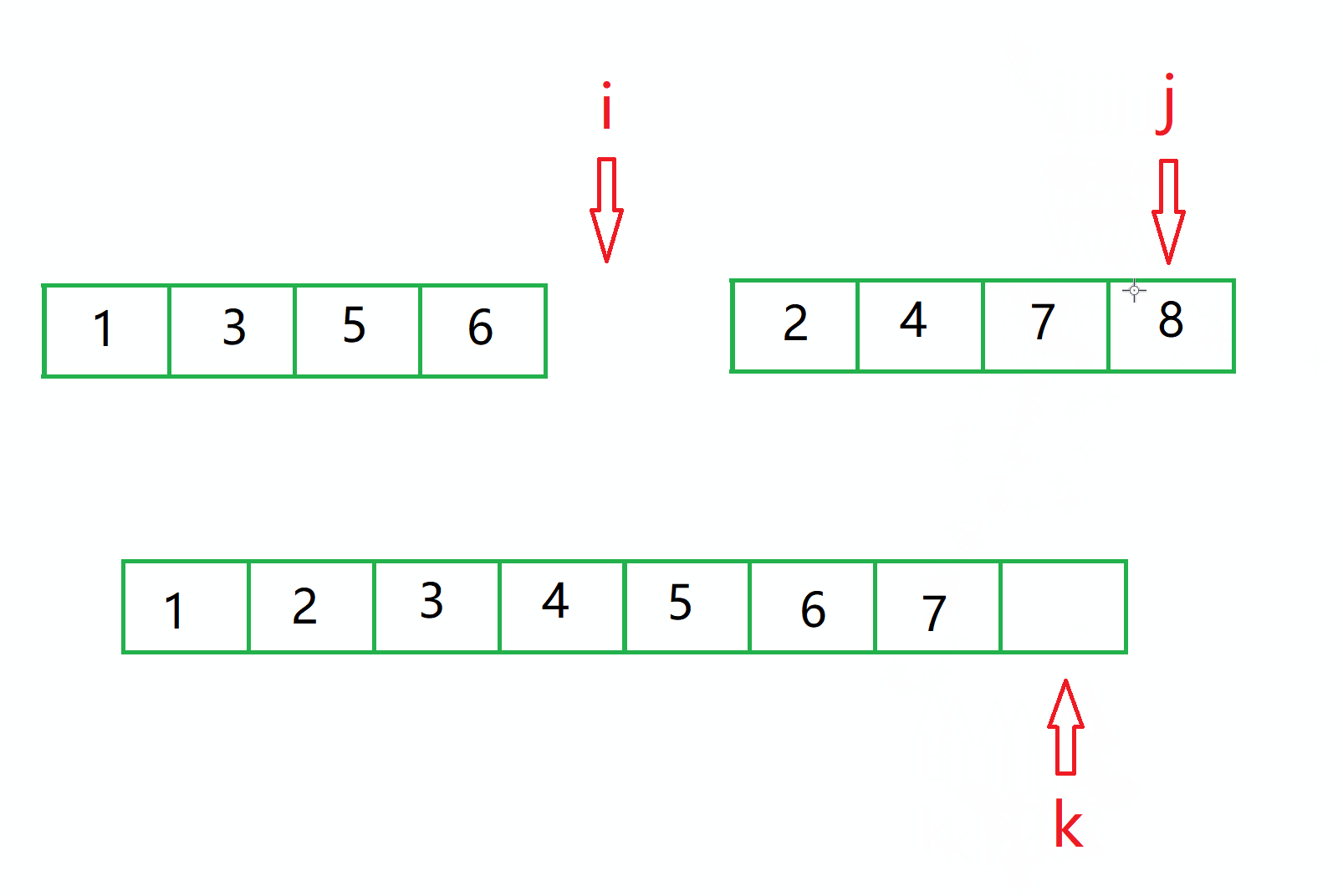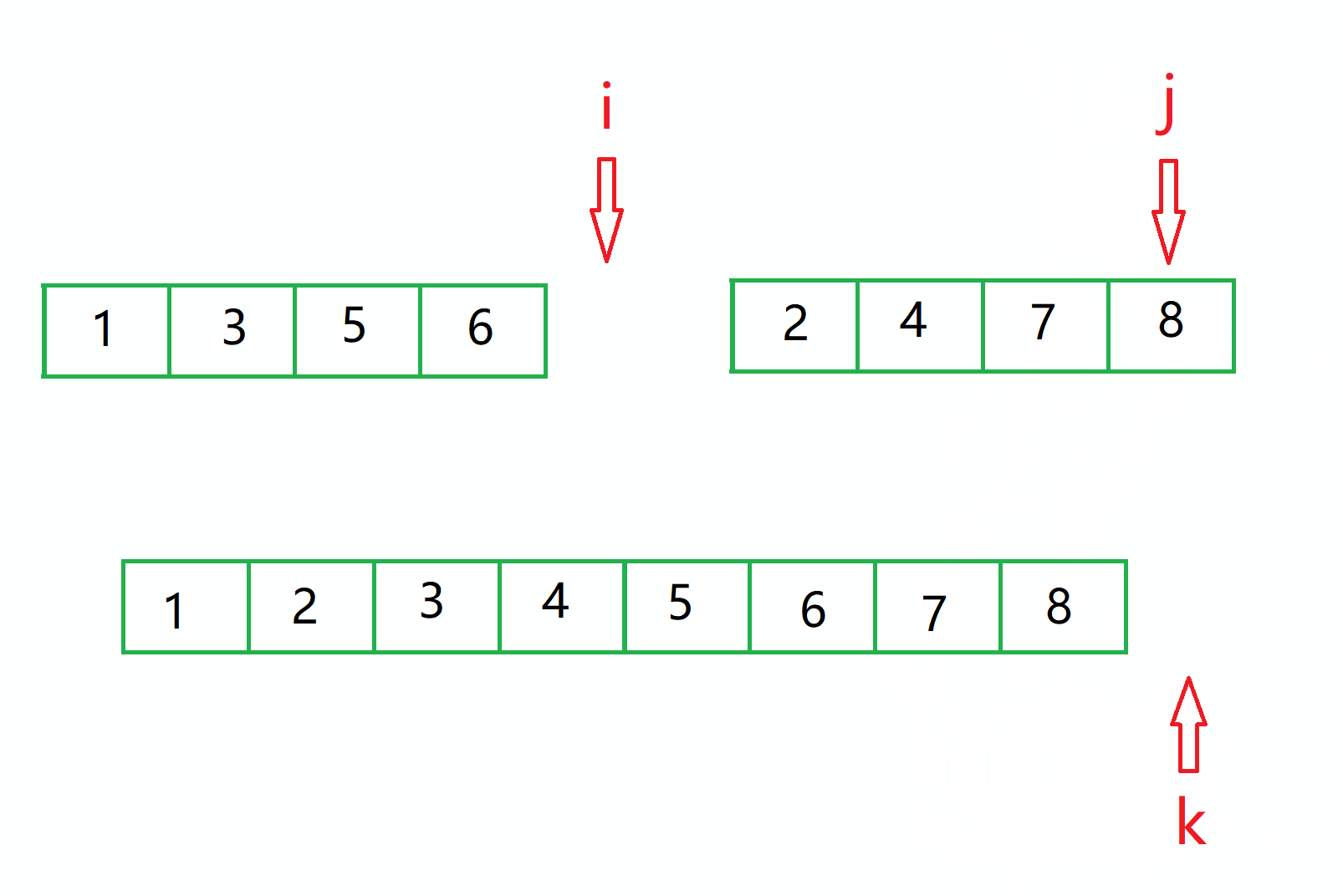
此时临时数组内的值就一定全部有序了,接下来我们需要将这个临时数组的值 搬到我们的原数组中。
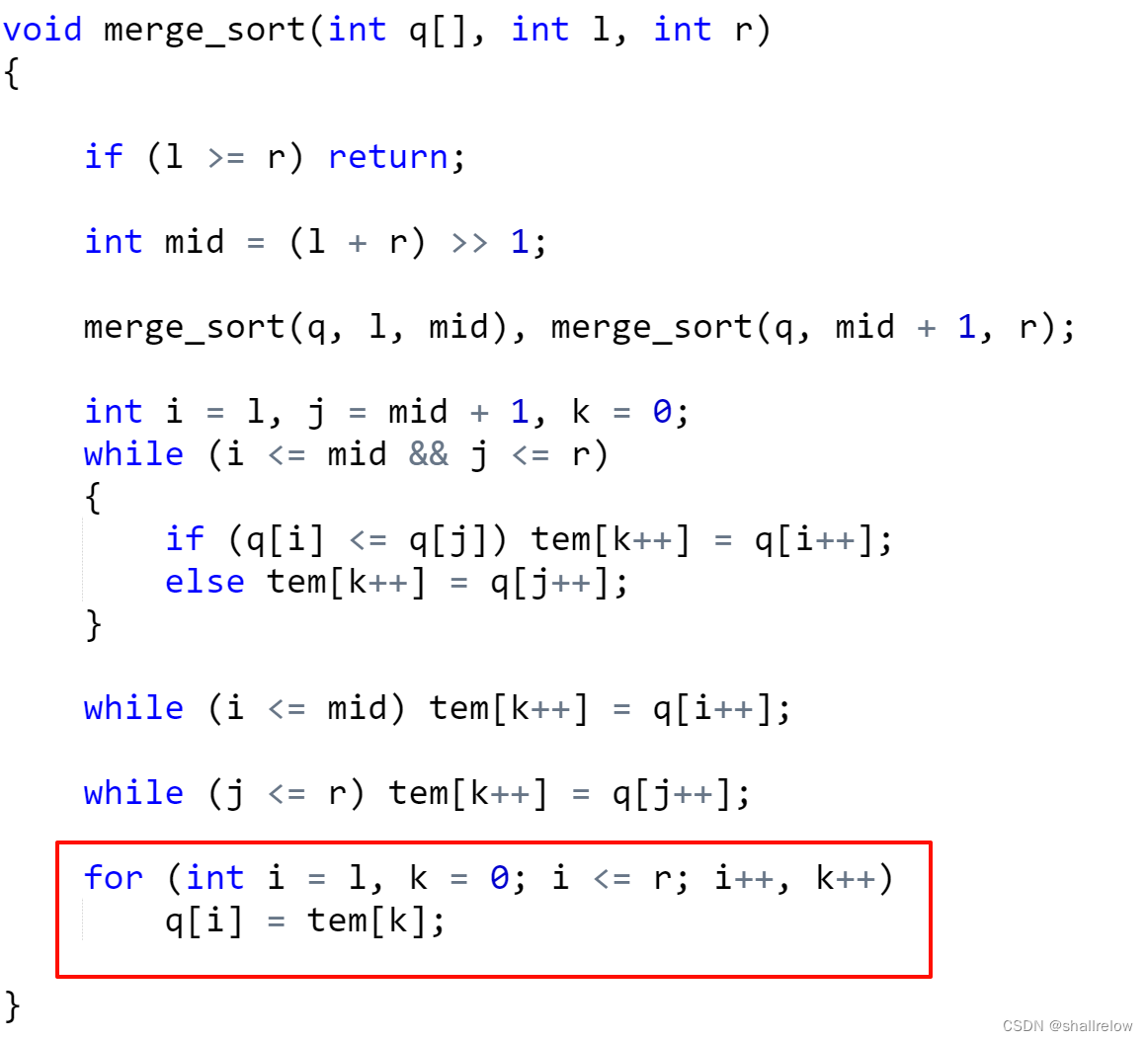
模拟完整过程:

完整代码如下:
#include <iostream>
using namespace std;const int N = 1e5+10;
int n;
int a[N], tem[N];void merge_sort(int q[], int l, int r)
{if (l >= r) return;int mid = (l + r) >> 1;merge_sort(q, l, mid), merge_sort(q, mid + 1, r);int i = l, j = mid + 1, k = 0;while (i <= mid && j <= r){if (q[i] <= q[j]) tem[k++] = q[i++];else tem[k++] = q[j++];}while (i <= mid) tem[k++] = q[i++];while (j <= r) tem[k++] = q[j++];for (int i = l, k = 0; i <= r; i++, k++)q[i] = tem[k];}int main()
{scanf("%d", &n);for (int i = 0; i < n; i++) scanf("%d", &a[i]);merge_sort(a, 0, n-1);for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}完
相关文章:

归并排序个人见解
归并排序个人见解 思路实现代码实现题目 思路实现 归并排序属于分治算法,分治算法有三个步骤: 分:将问题划分为多个规模较小的子问题,这些子问题与原始问题相似。治:递归地解决这些子问题。如果子问题足够小…...

软考初级网络管理员__网络单选题
1.观察交换机状态指示灯初步判断交换机故障,交换机运行中指示灯显示红色表示()。 警告 正常 待机 繁忙 2.通常测试网络连通性采用的命令是()。 Netstat Ping Msconfig Cmd 3.一台16端口的交换机可以产生()个冲突域? 1 4 15 16…...

22.2 正则表达式-数据验证、数据变换
1. 数据验证 正则表达可用于验证文本是否满足某种给定的模式。 正则表达式也是一种语言,因此在使用之前必须先对其进行编译,并将编译结果保存在一个Regexp类型的变量里。以下两个函数即返回该变量的指针。 re, err : regexp.Compile("^[a-zA-Z0-…...
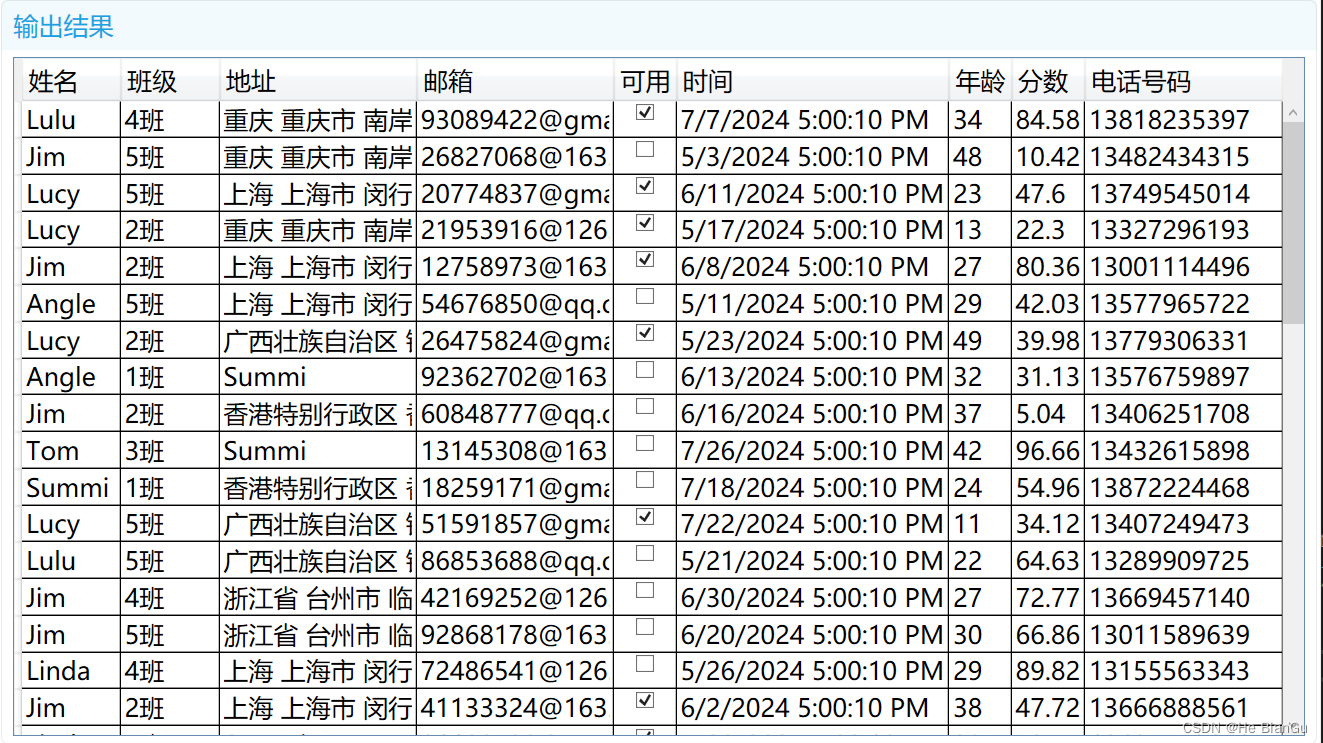
示例:WPF中应用DataGrid读取实体DisplayAttribute特性自动自动生成列名
一、目的:通过重写DataGrid的OnAutoGeneratingColumn方法实现根据定义特性自动生成列头信息功能 二、实现 <DataGrid ItemsSource"{local:GetStudents Count50}"/>实体定义如下 public class Student{[DataGridColumn("*")][Display(Na…...
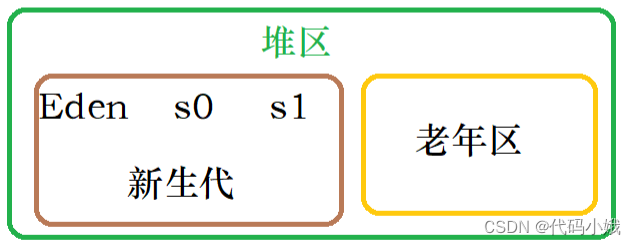
八股文之JVM
目录 1.JVM内存划分 2.JVM类加载过程 3.JVM垃圾回收机制GC 3.1.判断谁是垃圾 3.2.如何释放对应的内存 1.JVM内存划分 在一个Java程序运行起来之后,jvm就会从操作系统中申请一块内存,然后就会将该内存划分成多个部分,用于不同的用途。 …...

给wordpress添加限制游客浏览数量功能
wordpress游客只可以浏览5个内容,其它更多的是的需要注册后才能浏览。以下是使用自定义代码来实现这一功能的基本步骤: 创建一个自定义角色: 使用wp_create_roles函数来创建一个名为“访客”的新角色。 该角色将只具有阅读权限。 限制文章…...

[二分枚举]特殊密码锁
描述 有一种特殊的二进制密码锁,由n个相连的按钮组成(n<30),按钮有凹/凸两种状态,用手按按钮会改变其状态。 然而让人头疼的是,当你按一个按钮时,跟它相邻的两个按钮状态也会反转。当然&am…...

MT1434 找数字
题目 输入一个字符串(包含26个英文字母大小写及 . 空格,不含其他字符),把其中连续的数字作为一个整数,依次存放到一个数组中,输出这些整数的和。 格式 输入格式 输入字符串 输出格式 输出整型 样例1 输入: a12…...

2024年6月四六级考试复盘
一、考试情况 1.1四级考试情况 听力:一开始没有进入状态。总共对了9道。7.1*37.1*314.2*3 8.2 新闻听力:3/7 长对话:3/8 讲座/讲话:3/10 阅读:3.55*7 7.1*8 14.2 * 7 181.05 选词填空:保守估计7/1…...

join和left join性能比较
1、join和left join性能比较(AI生成) 在MySQL中,JOIN和LEFT JOIN的效率并不是绝对的,它们之间的性能差异取决于多种因素,如表的大小、使用的索引、查询的复杂性等。 一般来说: 如果两个表之间的连接条件能…...

Qt正则表达式
需求:对输入的内容进行限制 只能以字母或下划线开始不能以数字开始 不能有中文 字母,数字,下划线混合使用 QRegExp rx("^[A-Za-z_][A-Za-z0-9_]*$");QRegExpValidator validator(rx);QLineEdit edit;edit.setValidator(&va…...
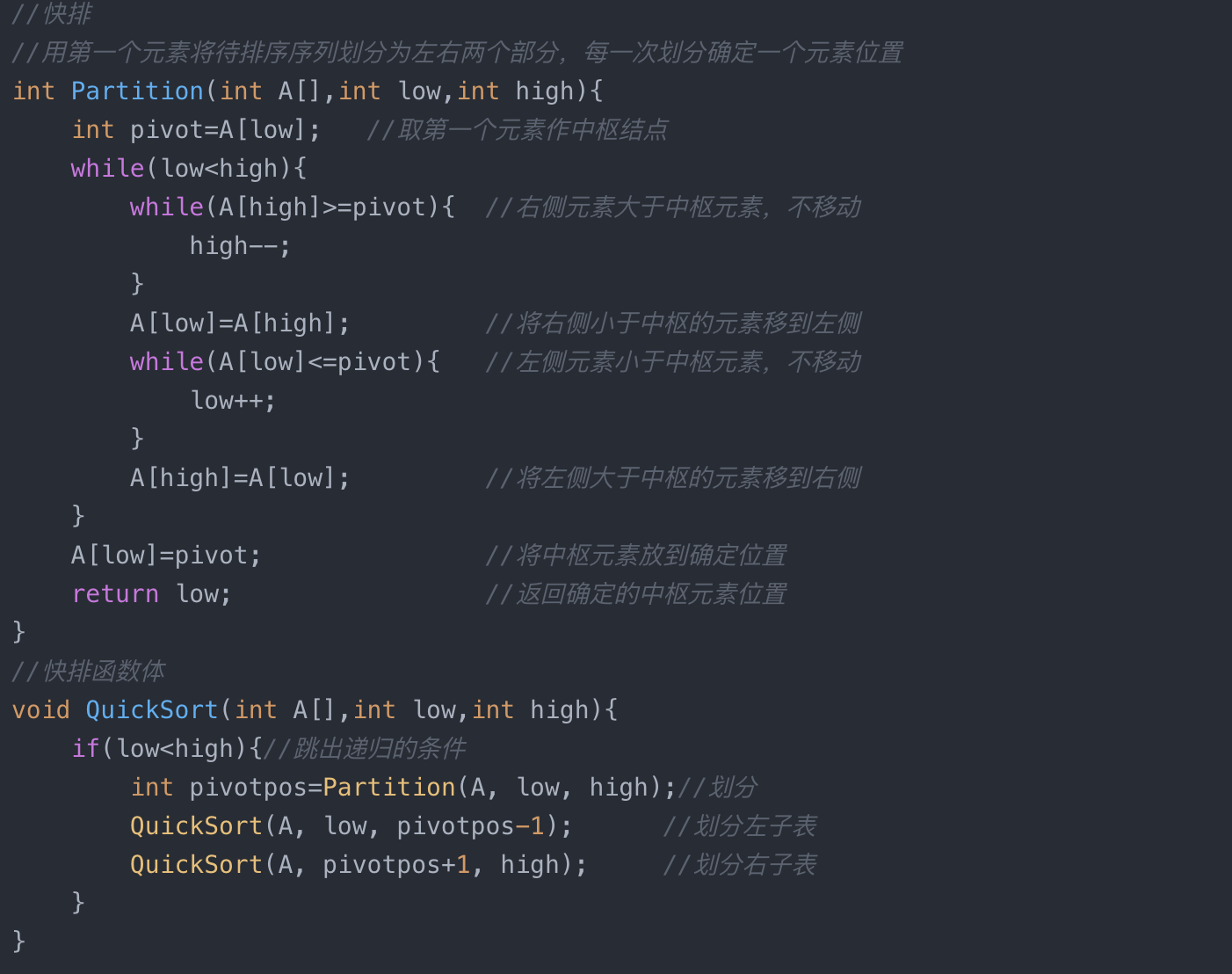
排序-快排算法对数组进行排序
目录 一、问题描述 二、解题思路 1.初始化 2.将右侧小于基准元素移到左边 3.将左侧大于基准元素移到右边 4.重复执行上面的操作 5.对分好的左、右分区再次执行分区操作 6.最终排序结果 三、代码实现 四、刷题链接 一、问题描述 二、解题思路 快排算法实现数组排序&am…...

flink学习-容错机制
checkpoint(检查点) 在flink中最重要的容错机制,就是checkpoint机制,使用checkpoint可以将之前某个时间点的所有的状态进行保存,这个存档就是checkpoint。 检查点的保存 周期性存储保存,间隔时间可以由用…...

InfluxDB技术分享
InfluxDB是一个开源的时间序列数据库,它被设计用来处理高速写入和查询大量的时间序列数据。以下是一份关于“InfluxDB在Java开发中的使用”的三十分钟技术分享内容概要: 1. 引言 (2分钟) 介绍时间序列数据和时间序列数据库的概念。引入InfluxDB的特点和…...
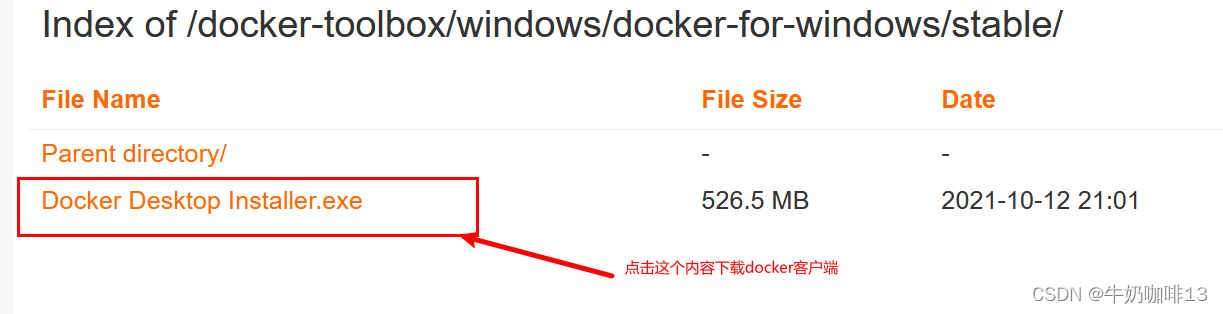
Windows10安装配置Docker客户端和WSL2与Hyper-V虚拟机
一、需求说明 需要在Windows系统中安装配置Docker的客户端,方便直接管理配置docker镜像容器内容。 二、Windows10安装Docker客户端步骤 2.1、下载安装Docker客户端 对于Windows 10以下的用户,推荐使用Docker Toolbox Windows安装文件:http://mirrors.aliyun.com/docker-…...
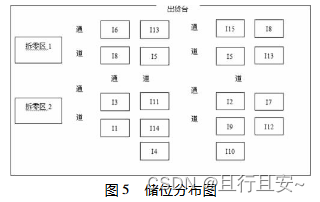
EIQ-ABC 分析法在配送中心储位分配中的应用
配送中心运作效率的高低主要取决于仓储业务流程的作业效率,在配送作业流程中,储位分配的是否合理性成为影响配送运作效率的重要因素。为实现储位的合理分配,提出通过对订单信息的分析,并应用 EIQ-ABC 分析法,以此实现缩…...
【安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试】
安装笔记-系列文章目录 安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试 文章目录 安装笔记-系列文章目录安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试 前言一、软件介绍名称:ttyd主页官方介绍特点 二、安装步骤测试版本…...
_基础部分)
React小记(一)_基础部分
1、项目搭建与结构 2、类组件和函数组件 主要区别:1、函数组件没有生命周期2、函数组件没有this指向3、函数组件没有状态4、函数组件通过hooks实现各种操作5、props在函数的第一个参数接收6、函数体相当于类组件的render函数import React from reactfunction App()…...

40、基于深度学习的线性预测设计(matlab)
1、原理及流程 深度学习的线性预测是一种利用深度神经网络模型进行线性回归预测的方法。其设计原理主要基于神经网络的层次化特性,利用多层感知器(MLP)等模型进行特征学习和非线性变换,从而提高线性预测的准确性。 设计流程如下…...

【初体验 threejs】【学习】【笔记】hello,正方体 3!
前言 为了满足工作需求,我已着手学习 Three.js,并决定详细记录这一学习过程。在此旅程中,如果出现理解偏差或有其他更佳的学习方法,请大家不吝赐教,在评论区给予指正或分享您的宝贵建议,我将不胜感激。 项…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
