Python — — GPU编程
Python — — GPU编程
要想将Python程序运行在GPU上,我们可以使用numba库或者使用cupy库来实现GPU编程。
壹、numba
Numba 是一个开源的 JIT (Just-In-Time) 编译器,它可以将 Python 代码转换成机器代码以提高性能。Numba 特别适用于需要高性能计算的科学计算和数值计算任务。也就是说可以将python程序编译为机器码,使其可以像c/c++、Java一样快速的运行。同样Numba不仅可以加速 CPU 上的 Python 代码,还可以利用 GPU 进行加速。
安装Numba:
pip install numba
一、机器码编程
1. 函数编写:
Numba 的核心功能是 @jit 装饰器,它可以将 Python 函数编译成优化的机器代码。
from numba import jit@jit(nopython=True)
def my_function(x):return x * xx = 112.0
print(my_function(x))
指定传递参数类型以及返回值类型,nopython表示不使用python编译而直接编译为机器码:
from numba import jit@jit('float64(float64)', nopython=True) # 指定输入和输出类型,括号内的是参数类型,括号外的是返回值类型
def my_function(x):return x * xx = 112.0
print(my_function(x))
从 Numba 0.15.1 版本开始,你可以使用 Python 类型注解来指定函数的参数类型:
from numba import jit@jit
def my_function(x: float) -> float:return x * x
2. 使用Numba函数:
使用 Numba 函数,我们可以像使用普通函数一样使用jit修饰过的函数:
result = my_function(10.5)
print(result) # 输出 110.25
Numba 特别适合于在 NumPy 数组上进行操作。你可以使用 NumPy 数组作为 Numba 函数的参数:
from numba import njit
import numpy as np@njit
def parallel_function(arr):return arr * 2arr = np.arange(10)
result = parallel_function(arr)
print(result)
3. 使用 Numba 的并行功能:
Numba 提供了并行执行的功能,可以使用 @njit 装饰器来替代 @jit,它会自动并行化循环:
from numba import njit
import numpy as np@njit
def parallel_function(arr):return arr * 2arr = np.arange(10)
result = parallel_function(arr)
print(result)
二、CUDA编程
1. 引入CUDA 模块:
from numba import cuda
2. 定义 GPU 核函数:
使用 @cuda.jit 装饰器定义 GPU 核函数,这与 CPU 加速中使用的 @jit 类似,但 @cuda.jit 指定了函数将在 GPU 上执行:
@cuda.jit
def gpu_kernel(x, y):# 核函数体,使用 CUDA 线程索引进行计算# 例如: position = cuda.grid(1)# if position < len(x):# y[position] = x[position] * x[position]
position = cuda.grid(1):其中cuda.grid(1)用于确定当前线程在执行的整个网格(grid)中的位置,这里的参数1表示一维的GPU网格索引,如果是cuda.grid(2)则表示二维的GPU网格索引。CUDA 的执行模型的概念:
- 线程(Thread):执行计算的最小单元。
- 块(Block):一组线程,它们可以共享数据并通过共享内存进行通信。
- 网格(Grid):由多个块组成,用于实现更大范围的并行性。
上面的代码表示的是对每一个元素分配一个GPU线程,通过
cuda.grid(1)来获取每一个线程,本质上也是获取每一个元素,然后再进行运算操作,通常情况下希望数组长度至少与线程数相等。因为如果线程总数大于数组长度,就会有多余的线程没有执行任何操作。例如,如果数组x只有 5 个元素,但配置了 32 个线程,那么只有前 5 个线程会计算和存储结果,其余 27 个线程将不会执行任何操作。
3. 设置执行配置:
GPU 核函数需要执行配置来确定并行执行的线程数和块数。这通过在函数调用时使用方括号指定:
threads_per_block = 256
blocks_per_grid = (n + (threads_per_block - 1)) // threads_per_block
gpu_kernel[blocks_per_grid, threads_per_block](x, y) # 给cuda.jit修饰的函数分配资源,并传入参数x 和 y
threads_per_block = 256:定义了每个块内的线程的个数,这里是256,如果是二维数组,那么需要使用元组的方式来进行定义,如:threads_per_block = (16, 16)。blocks_per_grid = (n + (threads_per_block - 1)) // threads_per_block:定义了整个网格(grid)中的块数量。它也是一个元组,n表示数组的长度,(n + (threads_per_block - 1)) // threads_per_block这种运算相当于一个向上取整的操作,保证了数组中的每一个元素都能分配一个GPU线程,因为一个原则是:线程数量要大于等于数组的个数。如果是二维数组需要这样定义网格中块的数量:blocks_per_grid = (m // threads_per_block[0], n // threads_per_block[1]),其中m表示行数,n表示列数。
4. 数据传输:
在 GPU 上执行计算之前,需要将数据从 CPU 内存传输到 GPU 内存,这通常使用 cuda.to_device() 方法完成:
x_device = cuda.to_device(x)
y_device = cuda.to_device(y)
5. 在 GPU 上分配内存:
如果 GPU 上的核函数需要额外的存储空间,可以使用 cuda.device_array() 在 GPU 上分配内存:
result_device = cuda.device_array_like(x_device)
6. 同步执行:
GPU 核函数的执行是异步的,可能需要调用 cuda.synchronize() 来确保 CPU 等待 GPU 计算完成:
cuda.synchronize()
7. 将结果从 GPU 传回 CPU:
计算完成后,使用 copy_to_host() 方法将 GPU 上的结果复制回 CPU 内存:
result = result_device.copy_to_host()
8. 实例一:
二维数组的GPU运算
import numpy as np
from numba import cuda@cuda.jit
def matrix_add(A, B, C, m, n):row, col = cuda.grid(2)if row < m and col < n:C[row, col] = A[row, col] + B[row, col]m, n = 1024, 1024
A = np.random.rand(m, n).astype(np.float32)
B = np.random.rand(m, n).astype(np.float32)C = np.zeros_like(A) # 创建与A形状相同的0数组
threads_per_block = (16, 16)
blocks_per_grid = (m // threads_per_block[0], n // threads_per_block[1])
matrix_add[blocks_per_grid, threads_per_block](A, B, C, m, n)
print(C)
9. 实例二:
GPU显存与主机内存之间的通信
from numba import cuda
import numpy as np# 在主机上创建一个NumPy数组
host_array = np.array([1, 2, 3, 4], dtype=np.int32)# 使用cuda.to_device将主机数组复制到GPU
device_array = cuda.to_device(host_array)# 确保数据传输完成
cuda.synchronize()# 使用.copy_to_host()方法将GPU数组复制回主机数组
host_result = device_array.copy_to_host()
print(host_result)# 释放GPU内存
del device_array
10. 实例三:
一维数组的GPU运算
from numba import cuda
import numpy as np# 定义一个简单的cuda内核
@cuda.jit()
def add_kernel(x, y, z, n):i = cuda.grid(1) if i < n: # 确保不会超出数组边界z[i] = x[i] + y[i]# 主函数
def main():n = 256x = cuda.device_array(n, dtype=np.int32) # 直接在GPU上创建数据,占用GPU显存y = cuda.device_array(n, dtype=np.int32)z = cuda.device_array(n, dtype=np.int32)# 初始化数据for i in range(n):x[i] = iy[i] = 2 * i# 计算线程块大小和网格大小, 线程块是一组可以同时执行的线程集合threadsperblock = 32 # 这意味着每个线程块将包含256个线程。blockspergrid = (n + (threadsperblock - 1)) // threadsperblock # 定义每个网格内的块的个数# 启动内核add_kernel[blockspergrid, threadsperblock](x, y, z, n)# 将结果从GPU复制回主机result = z.copy_to_host()print(result)if __name__ == '__main__':main()
贰、cupy
CuPy 是一个与 NumPy 兼容的库,提供了 NumPy 相同的多维数组 API,但是所有的数值计算都在 GPU 上执行。CuPy 底层使用 CUDA,但是 API 更简洁,使用起来比直接使用 CUDA 更加方便。
使用cupy时,我们首先需要将CUDA的环境给配置好,包括CUDA Toolkit
一、安装cupy:
pip install cupy
二、使用cupy:
1. 导入 CuPy:
import cupy as cp
2. 创建 CuPy 数组
可以使用与 NumPy 类似的函数来创建 CuPy 数组。CuPy 数组是在 GPU 上的多维数组。
# 创建一个全零数组
x = cp.zeros((3, 3))# 创建一个全一数组
y = cp.ones((2, 2))# 从 Python 列表创建数组
z = cp.array([[1, 2], [3, 4]])
3. 基本运算
# 矩阵乘法
result = cp.dot(x, z)# 元素乘法
elementwise_product = x * y# 元素加法
sum_result = x + z# 计算平方根
sqrt_result = cp.sqrt(x)
4. 利用 GPU 加速
# 计算数组的总和
total = x.sum()# 计算数组的均值
mean_value = x.mean()
5. 与 NumPy 的互操作性
# 将 NumPy 数组转换为 CuPy 数组
numpy_array = np.random.rand(10)
cupy_array = cp.array(numpy_array)# 将 CuPy 数组转换回 NumPy 数组
numpy_array_again = cupy_array.get()
6. 使用随机数生成
# 生成随机数数组
random_array = cp.random.rand(3, 3)# 生成符合正态分布的随机数数组
normal_array = cp.random.normal(0, 1, (3, 3))
7. 广播
# 广播示例
a = cp.array([1, 2, 3])
b = cp.array([[1], [2], [3]])
result = a + b # 结果是一个 3x3 的数组
8. 索引和切片
# 获取第二行
second_row = z[1]# 切片操作
upper_triangle = z[cp.triu(cp.ones((3, 3), dtype=cp.bool_))]
9. 内存管理
CuPy 使用 GPU 内存,当不再需要 CuPy 数组时,应该释放它们以避免内存泄漏。
del x, y, z
cp.get_default_memory_pool().free_all_blocks()
10. 实例一:
import cupy as cp# 创建一个Cupy数组(自动在GPU上)
x = cp.array([1., 2., 3., 4., 5.])
y = cp.sqrt(x)
print(y)# 将Cupy数组转换回Numpy数组(如果有需要的话)
z = cp.asnumpy(y)print(z)
11. 实例二:
import cupy as cp# 创建两个随机的浮点型 CuPy 数组,相当于 NumPy 中的矩阵
A = cp.random.rand(3, 3).astype('float32') # 3x3 矩阵
B = cp.random.rand(3, 3).astype('float32') # 另一个 3x3 矩阵# 执行矩阵乘法
C = cp.dot(A, B) # 或者使用 @ 操作符 C = A @ B# 打印结果
print("矩阵 A:\n", A)
print("矩阵 B:\n", B)
print("矩阵 A 和 B 的乘积:\n", C)# 将 CuPy 数组转换回 NumPy 数组(如果需要)
import numpy as np
numpy_C = C.get() # 将 CuPy 数组转换为 NumPy 数组# 执行一些基本的 NumPy 操作,比如求和
sum_C = cp.sum(C) # 在 GPU 上计算 C 的总和# 打印 C 的总和
print("矩阵 C 的总和:", sum_C)# 释放不再使用的 CuPy 数组以节省 GPU 内存
del A, B, C
cp.get_default_memory_pool().free_all_blocks()
相关文章:

Python — — GPU编程
Python — — GPU编程 要想将Python程序运行在GPU上,我们可以使用numba库或者使用cupy库来实现GPU编程。 壹、numba Numba 是一个开源的 JIT (Just-In-Time) 编译器,它可以将 Python 代码转换成机器代码以提高性能。Numba 特别适用于需要高性能计算的…...

C#中的枚举类-自定义属性
在实际开发过程中,我们常常会用到枚举类,使用枚举的时候往往有着各种使用条件,如何给枚举加入使用条件呢? 答案就是我们的——自定义属性 废话不多说,上代码 枚举类 首先我们要有一个枚举类 public enum XXXX枚举…...

多态深度剖析
前言 继承是多态的基础, 如果对于继承的知识还不够了解, 可以去阅读上一篇文章 继承深度剖析 基本概念与定义 概念: 通俗来说,就是多种形态。具体点就是去完成某个行为, 当不同的对象去完成时会产生出不同的状…...
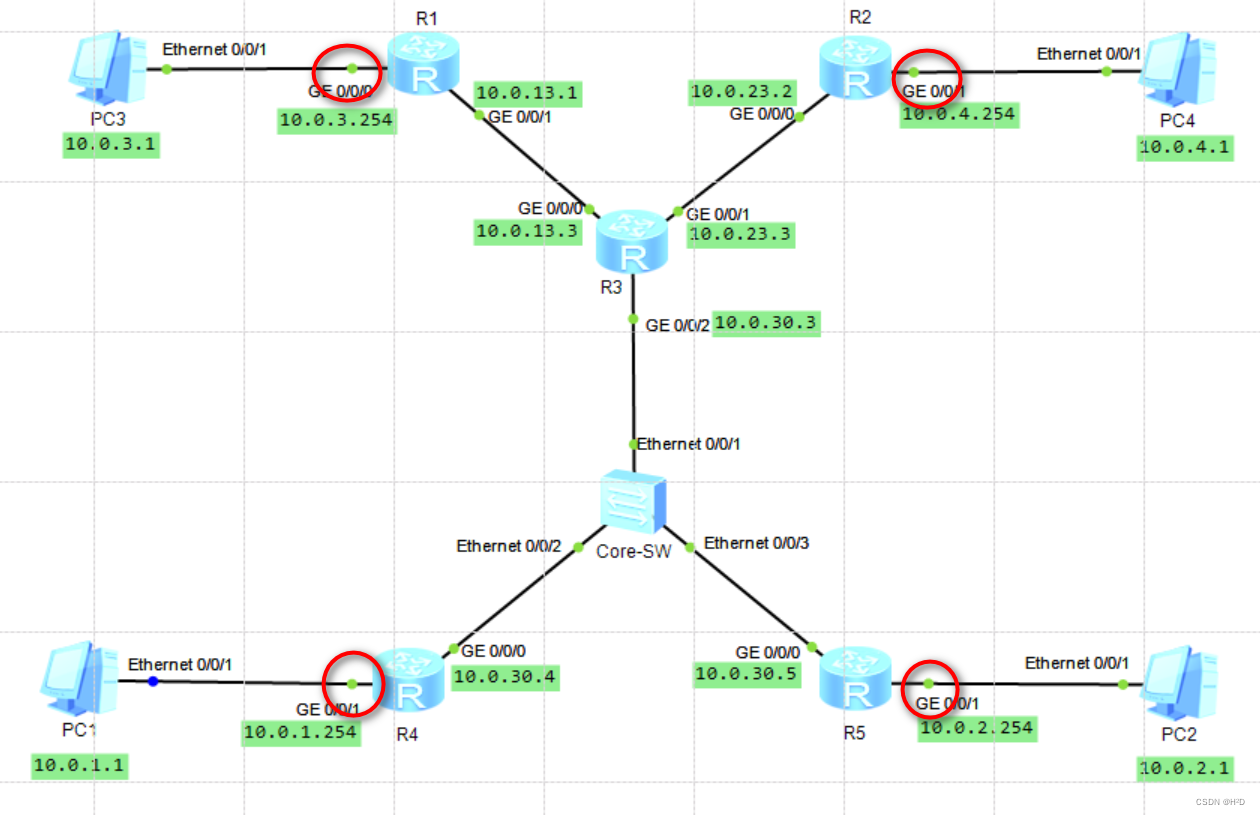
OSPF被动接口配置(华为)
#交换设备 OSPF被动接口配置 一、基本概念 OSPF被动接口,也称为抑制接口,即将路由器某一接口配置为被动接口后,该接口不会再接受和发送OSPF报文 二、使用场景 在路由器与终端相近或者直接相连的一侧配置被动接口 因为OSPF会定期发送报文…...

Android --- 异步操作
同步和异步的差异 同步:在发生某件事后什么也不做,直到该事件完成后,再继续进行 异步:在某件事发生后,可以在等待他完成的时候去处理其他事件,等到该事件发生完成后,再回过头来处理它。 异步…...
MOS管专题--->(10)MOS管的封装)
(55)MOS管专题--->(10)MOS管的封装
(10)MOS管的封装 1 目录 (a)IC简介 (b)数字IC设计流程 (c)Verilog简介 (d)MOS管的封装 (e)结束 1 IC简介 (a)在IC设计中,设计师使用电路设计工具(如EDA软件)来设计和模拟各种电路,例如逻辑电路、模拟电路、数字信号处理电路等。然后,根据设计电路的…...

超高清图像生成新SOTA!清华唐杰教授团队提出Inf-DiT:生成4096图像比UNet节省5倍内存。
清华大学唐杰教授团队最近在生成超高清图像方面的新工作:Inf-DiT,通过提出一种单向块注意力机制,能够在推理过程中自适应调整内存开销并处理全局依赖关系。基于此模块,该模型采用了 DiT 结构进行上采样,并开发了一种能…...
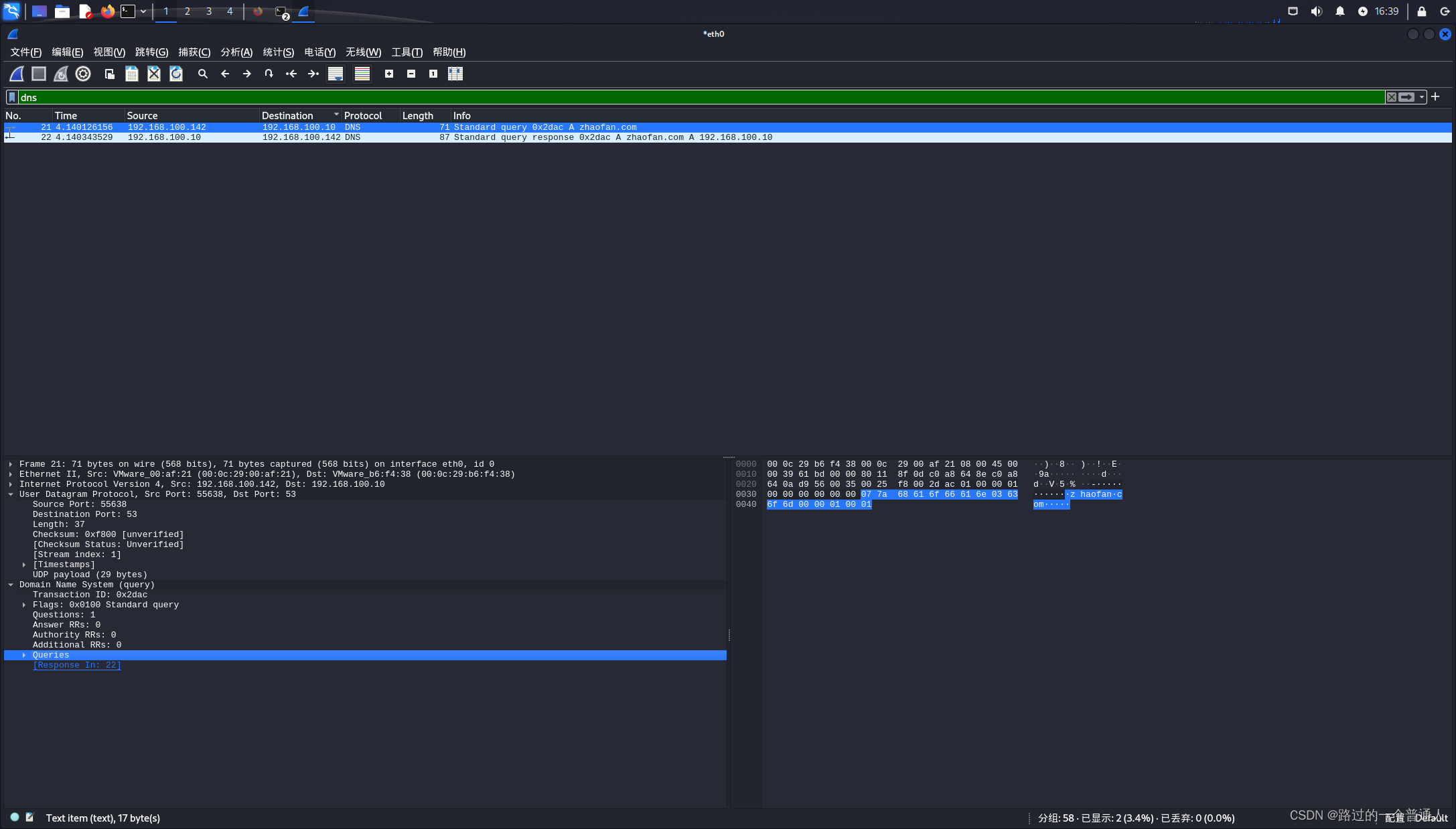
网络安全 - DNS劫持原理 + 实验
DNS 劫持 什么是 DNS 为什么需要 DNS D N S \color{cyan}{DNS} DNS(Domain Name System)即域名系统。我们常说的 DNS 是域名解析协议。 DNS 协议提供域名到 IP 地址之间的解析服务。计算机既可以被赋予 IP 地址,也可以被赋予主机名和域名。用…...
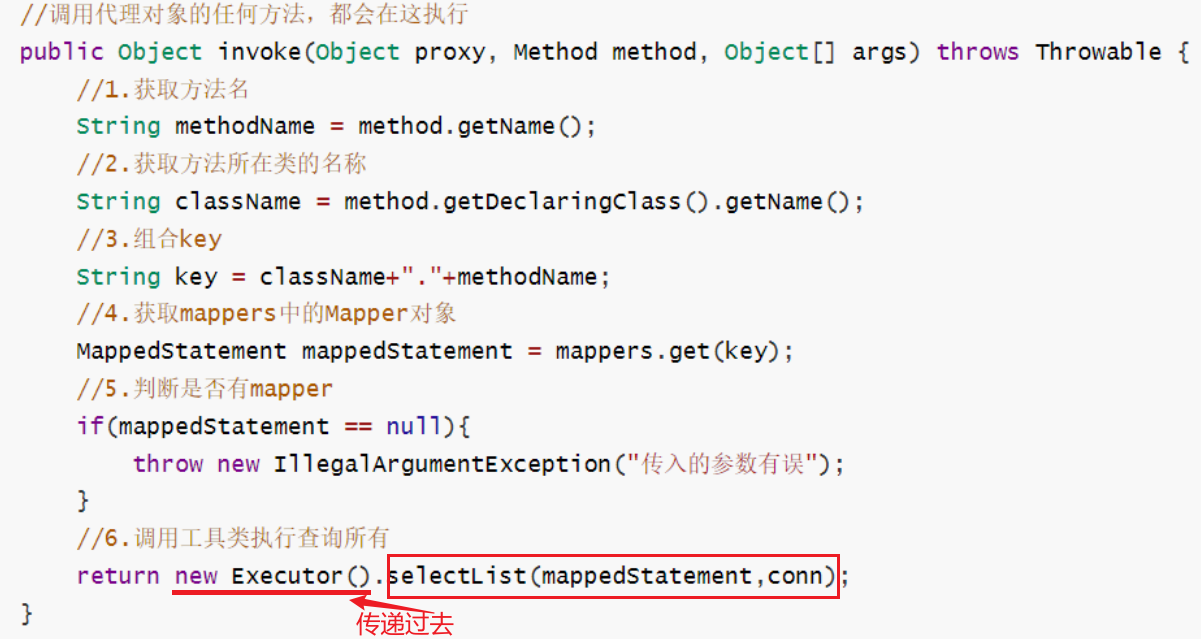
MyBatis的运行原理
目录 1、目的:梳理一下MyBatis运行时的几个对象,我们需要搞清楚他们的作用,进而需要理解mybatis的整个工作流程和执行原理。 2、简要概括各个类 2.1 Resources 作用:编写资源加载类,使用类加载器加载 配置文件(myb…...

算法题解记录29+++全排列(百日筑基)
一、题目描述 题目难度:中等 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示…...

苹果AI功能,AI训练数据缺乏,SD3推出,MJ6推出新特性
更多信息: https://agifun.love 智源社区 2024智源大会议程公开丨大模型前沿探索 2024年6月14日-15日,第6届北京智源大会将以线下与线上结合的形式召开,线下会场设在中关村国家自主创新示范区会议中心。2024智源大会再次以全球视野&#x…...

超越中心化:Web3如何塑造未来数字生态
随着技术的不断发展,人们对于网络和数字生态的期望也在不断提升。传统的中心化互联网模式虽然带来了便利,但也暴露出了诸多问题,比如数据滥用、信息泄露、权力集中等。在这样的背景下,Web3技术应运而生,旨在打破传统中…...
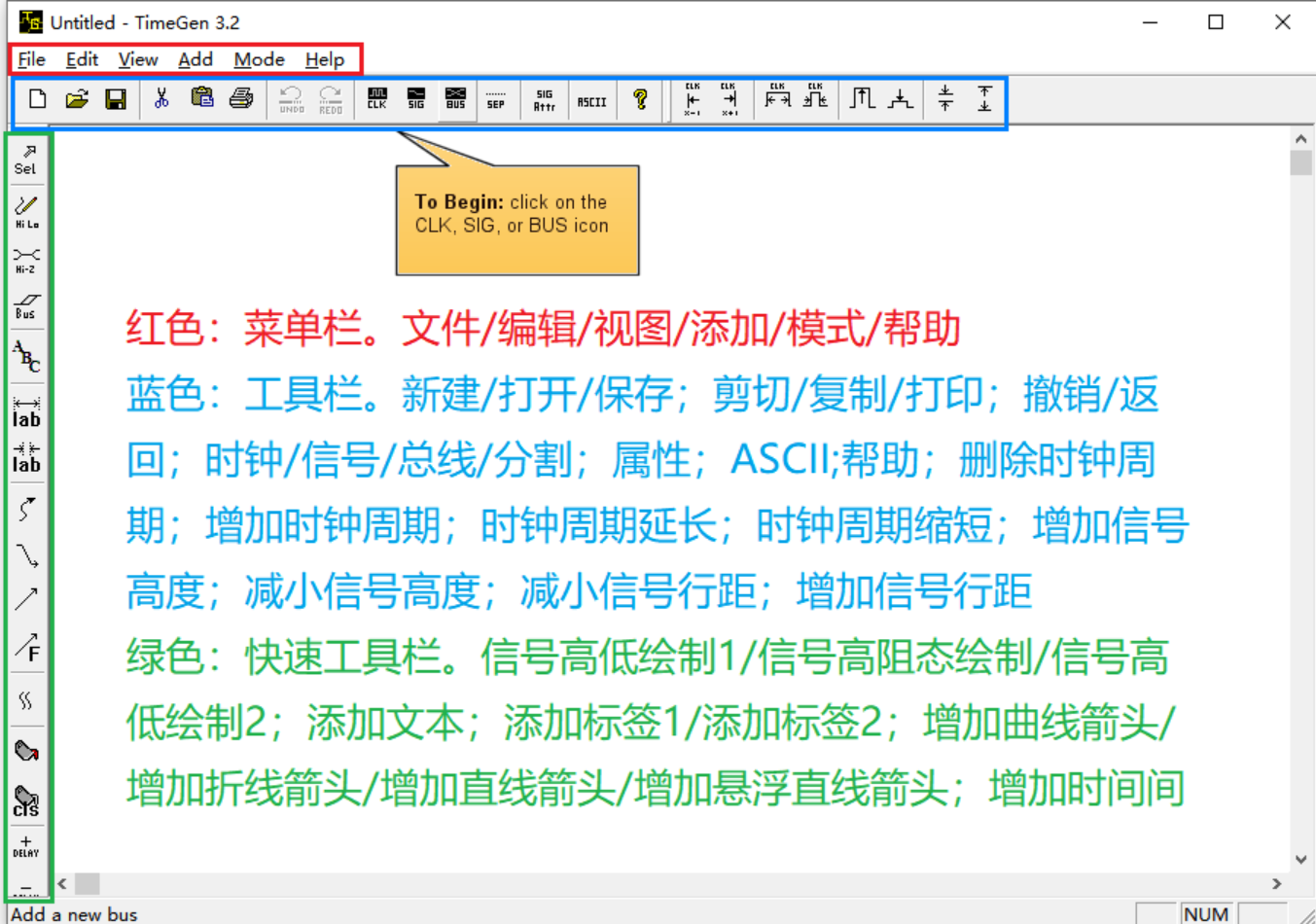
【ic-tool】timegen使用
一、前言 TimeGen是一个用于时序波形编辑的CAD工具,它允许数字设计工程师快速有效地绘制数字时序图。TimeGen时序图可以很容易地导出到其他窗口程序,如microsoftword,用于编写设计规范。可直接从官网下载TimeGEN软件:TimeGen Pro…...
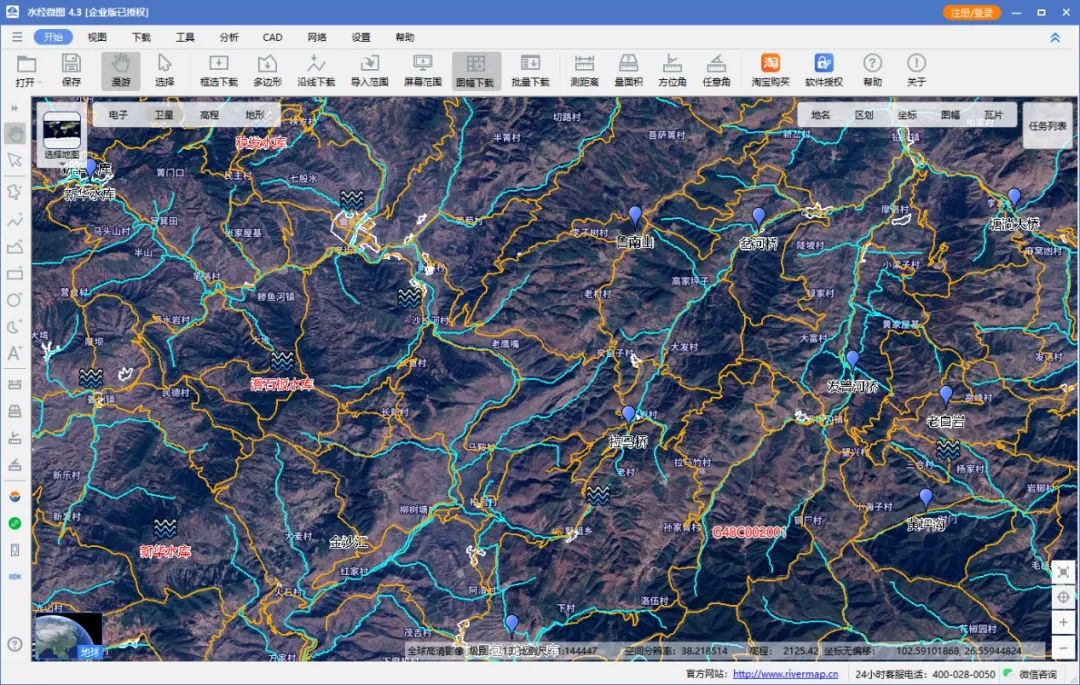
1:25万基础电子地图(云南版)
我们在《50幅1:25万基础电子地图(四川版)》一文中,为你分享过四川的50幅基础电子地图。 现在我们再为你分享云南的1:25万基础电子地图,你可以在文末查看该数据的领取方法。 基础电子地图云南版 下载后可以看到该数据…...
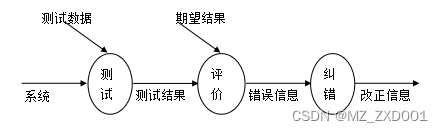
springboot宠物领养系统-计算机毕业设计源码07863
摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存…...

牛客热题:最长回文子串
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:最长回文子串题目链接方法一&am…...

如何访问寄存器
标题 方式一:对地址进行宏定义方式二:用结构体封装寄存器 访问寄存器是CPU执行程序的基础,每种CPU架构都有其特定的寄存器集合和访问方式。 方式一:对地址进行宏定义 #define GPIOA_BASE ((unsigned int)0x48000000) #define GPI…...

苍穹外卖笔记-18-修改密码、bug记录
文章目录 1 修改密码1.1 需求分析和设计1.2 代码实现1.2.1 admin/EmployeeController1.2.2 EmployeeService1.2.3 EmployeeServiceImpl 1.3 功能测试 2 bug记录 1 修改密码 完结的时候发现还有一个接口未实现。这里补充 1.1 需求分析和设计 产品原型: 业务规则&am…...

java如何截取字符串
如果想在一个字符串中截取一段字符,形成新的字符,那么在java中途需要用到substring语句 substring的语法格式是 str.substring(beginindex,endindex) 其中str是字符串 beginindex是起始索引,endindex是结束索引 截取的字符串包含起始索引…...

虚拟淘宝-Virtual-Taobao论文解读(AAAI2019)
目录 1 论文简介 2 文章的主要贡献 3 文章技术的简要说明 4 技术的详细说明 4.1 GAN-SD:生成客户特征 4.2 MAIL:生成交互过程 4.3 ANC:动规范约束 5 实验设定及结果 6 结论 7 参考 1 论文简介 南京大学LAMDA团队的侍竞成、俞扬等…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
