IEEE754、linear11、linear16浮点数应用原理
IEEE754、linear11、linear16浮点数应用原理
- 1 浮点数应用
- 1.1 IEEE754 浮点数标准
- 1.2 PMBUS浮点数格式
- 2 浮点数原理
- 2.1 IEEE754 浮点数解析
- 2.2 PMBUS浮点数解析
- 3 浮点数代码应用
- 3.1 IEEE754 浮点数应用
- 3.1.1 将浮点变量赋值,直接打印整型(32位)变量
- 3.1.2 将整型(32位)变量赋值,直接打印浮点数变量
- 3.2 PMBUS 浮点数应用
- 3.2.1 浮点数转化为linear11格式
- 3.2.2 浮点数转化为linear16格式
- 3.2.3 linear格式转化为浮点数
- 4 总结
1 浮点数应用
1.1 IEEE754 浮点数标准
IEEE754标准,规定可4种标识浮点数值得方式,分别是但精确度(32位)、
双精度(64位)、延伸单精度(43bit以上)、延伸双精度(79bit以上)。其中32位模式有强制要求,其他都是选择性的。C语言float通常指单精度,double通常指双精度浮点数。
1.2 PMBUS浮点数格式
PMBUS中数据格式通常指线性数据格式(linear格式),常见应用格式有linear11和linear16。
2 浮点数原理
2.1 IEEE754 浮点数解析
以32位浮点数为准进行解析,长度32位浮点数的存储格式为4个字节,发送时按尾数低位、尾数中位、尾数高位、阶码及符号位的先后顺序。格式如下表所示。
符号位S 阶码位 E 尾数位 M (小数部分参数)
D31 D30-D23 D22-D16 D15-D8 D7-D0
浮点数符号 阶码 尾数高位 尾数中位 尾数低位

浮点数值 = (-1)S * 2(E-127) * (1 + M2(-23))
例如1:当32位浮点数为40H、A0H、00H、00H,即S=0,E=129,M=221,则:
浮点数值 = (-1)0 * 2(129-127) * (1 + 2212(-23))= 141.25=5.0 。
例如2:一个浮点数4.538,推算出IEEE754(32)标准二进制表示,则
(1)小数部分(最高23位00~22)
位00:0.538 *2 = 1.076 **** 取1
位01:0.076 *2 = 0.152 **** 取0
位02:0.152 *2 = 0.304 **** 取0
位03:0.304 *2 = 0.608 **** 取0
位04:0.608 *2 = 1.216 **** 取1
位05:0.216 *2 = 0.432 **** 取0
位06:0.432 *2 = 0.864 **** 取0
位07:0.864 *2 = 1.728 **** 取1
位08:0.728 *2 = 1.456 **** 取1
位09:0.456 *2 = 0.912 **** 取0
位10:0.912 *2 = 1.824 **** 取1
位11:0.824 *2 = 1.648 **** 取1
位12:0.648 *2 = 1.296 **** 取1
位13:0.296 *2 = 0.592 **** 取0
位14:0.592 *2 = 1.184 **** 取1
位15:0.184 *2 = 0.368 **** 取0
位16:0.368 *2 = 0.736 **** 取0
位17:0.736 *2 = 1.472 **** 取1
位18:0.472 *2 = 0.944 **** 取0
位19:0.944 *2 = 1.888 **** 取1
位20:0.888 *2 = 1.776 **** 取1
位21:0.776 *2 = 1.552 **** 取1
位22:0.552 *2 = 1.104 **** 取1
(2)则对于4.538的二进制表示
二进制:100.10001001101110100101111
尾数的要求转换:1.0010001001101110100101111 * 22整数位为1,小数点变换的位数n为2的n次,往左移动为正n,往右移动为负n。
所以阶码为:2+127=129 ,尾数为:0010001001101110100101111 (25位)
符号位为:0(正数),尾数位23位,0010001001101110100101111最后两位(11)去掉,第24位0舍1入。
则二进制32位:01000000100100010011011101001011+1
所以4字节为0x 40 91 37 4C。
同理,双精度浮点数变换原理相同,只是各部分尾数有差异而已。
2.2 PMBUS浮点数解析
(1)linear11格式解析
linear11数据格式由2个字节组成
字节1 字节0
N(为补码)(指数) Y(为补码)(尾数)
7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0

转换时,需将N Y转化为其原码进行计算
linear11数据数值 = Y(原码)* 2N(原码)。(Y:-1024+1023,N:-16+15)
例如1:linear11数据为0x97AB,解析数据:
(1)N = 0b10010,Y=0b11110101011,
N(原码)= 0b11110 = -14;
Y(原码)= 0b10001010101 = -85;
(2)数值 = -85 * 2-14,
例如2:数值为-45.39转化为linear11格式如何计算:
(1)先取Y值,将数值逐次乘以2,使得结果在±512~±1024之间,-45.39乘以2的4次方为-726.24,然后四舍五入取整为-726为Y值,
(2)N值为第一步的4次,取反,为-4
(3)最终结果为0xE52A
例如3:数值为-0.007转化为linear11格式如何计算:
(1)先取Y值,将数值逐次乘以2,使得结果在±512±1024之间,-0.007乘以2的16次方为-458.752,N值范围为(N:-16+15),所以不能继续乘2,然后四舍五入取整为-459为Y值,
(2)N值为第一步的16次,取反,为-16
(3)最终结果为0x8635
根据以上举例可知确定,在原有的数据基础上进行乘2(最大16次)运算,或者除2(最大15次)运算,若超次数则立即停止,在不超次数情况下使结果数据 坐落在±512~±1024之间,然后确定Y值和N值。
同理linear16原理雷同,注意各部分的数值范围。
3 浮点数代码应用
3.1 IEEE754 浮点数应用
使用共用体的方式实现数据快速格式转换,编译器会自动将单精度或者双精度浮点数存储在内存中,存储在内存中的数据就是16进制格式,故我们使用共用体实现数据快速转换,不需要进行数据推演,示例如下:
3.1.1 将浮点变量赋值,直接打印整型(32位)变量
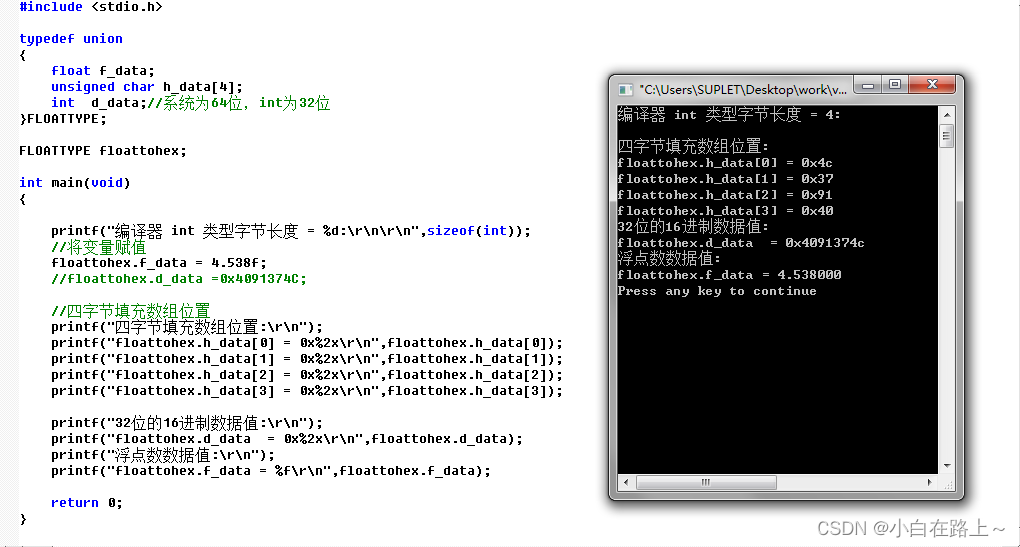
3.1.2 将整型(32位)变量赋值,直接打印浮点数变量
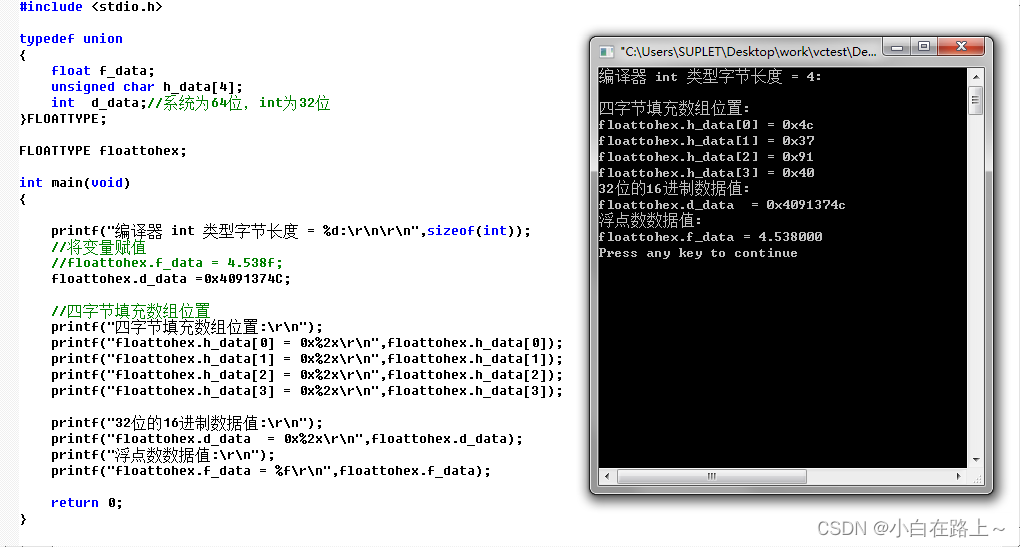
3.2 PMBUS 浮点数应用
3.2.1 浮点数转化为linear11格式
根据在原有的数据基础上进行乘2(最大16次)运算,或者除2(最大15次)运算,若超次数则立即停止,在不超次数情况下使结果数据 坐落在±512~±1024之间,然后确定Y值和N值。代码如下。
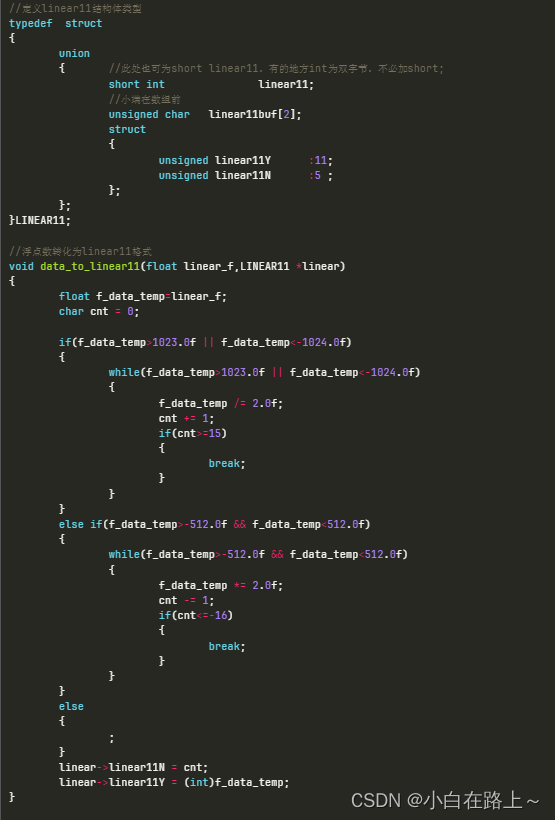
3.2.2 浮点数转化为linear16格式
在原有的数据基础上进行乘2(最大16次)运算,或者除2(最大15次)运算,若超次数则立即停止,在不超次数情况下使结果数据 坐落在±16384~±32768之间,然后确定Y值和N值。代码如下。
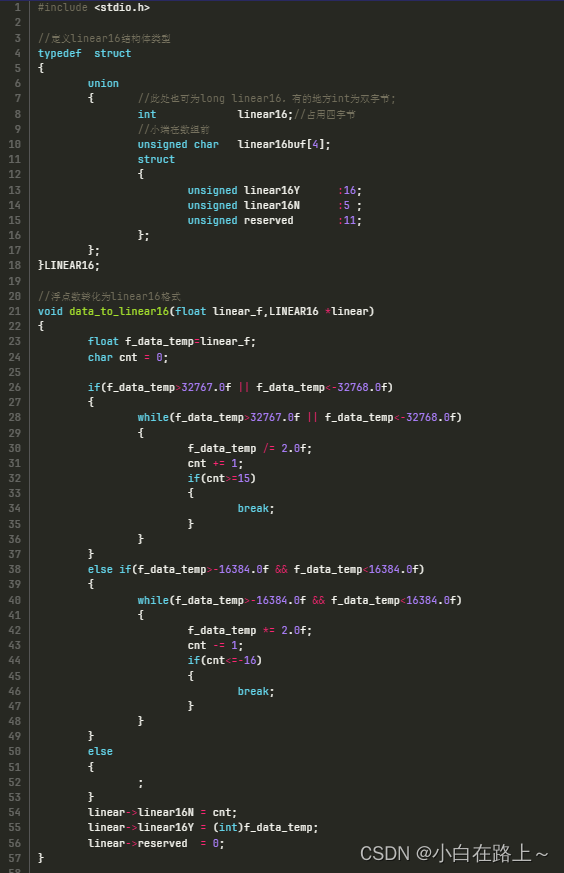
3.2.3 linear格式转化为浮点数
根据公式,数据数值 = Y(原码)* 2N(原码)的格式,首先位定义我们使用有符号形式定义,然后获取对应Y和N值,引用math.h头文件,包含了pow函数,即可实现数据转换。
(1)linear11转化为浮点数。
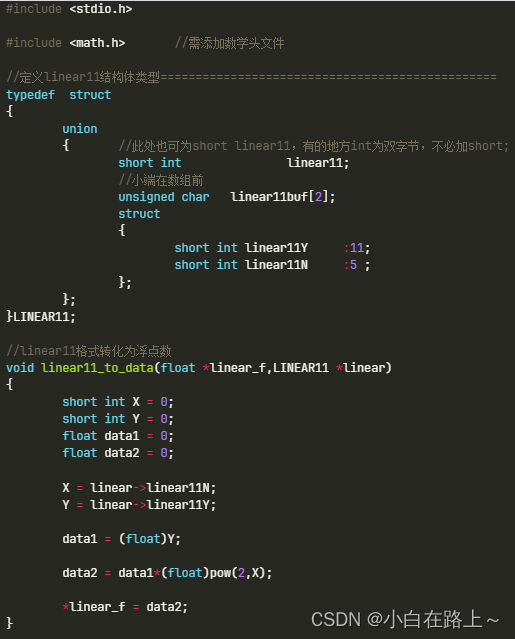
(2)linear16转化为浮点数。
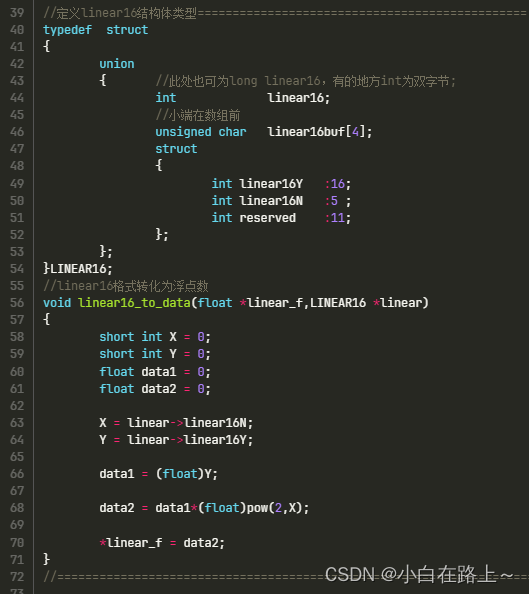
4 总结
关于IEEE754和PMBUS浮点数的运算常见的就是以上几种,实际使用时运用了结构体及共用体定义数据类型,运算中不必再次进行位运算等操作,关于结构体及共用体已在前面中有指导代码。
相关文章:

IEEE754、linear11、linear16浮点数应用原理
IEEE754、linear11、linear16浮点数应用原理 1 浮点数应用1.1 IEEE754 浮点数标准1.2 PMBUS浮点数格式 2 浮点数原理2.1 IEEE754 浮点数解析2.2 PMBUS浮点数解析 3 浮点数代码应用3.1 IEEE754 浮点数应用3.1.1 将浮点变量赋值,直接打印整型(32位…...
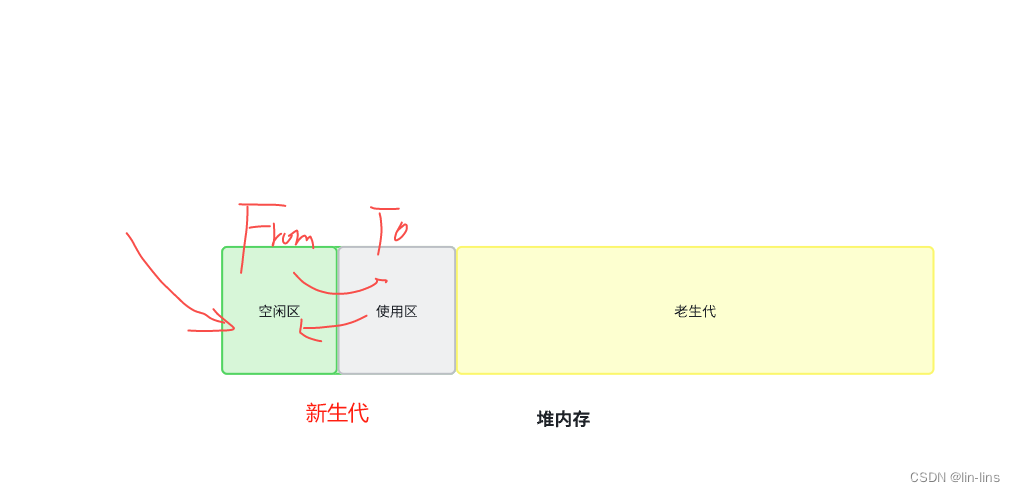
6、 垃圾回收 浏览器事件循环
垃圾回收 & 浏览器事件循环 垃圾回收引用计数算法标记清除(mark-sweep)算法标记整理(Mark-Compact)算法 内存管理浏览器事件循环宏任务微任务整体流程 垃圾回收 垃圾回收,又称为:GC(garbag…...

Java多线程面试重点-2
16.Synchronized关键字加在静态方法和实例方法的区别? 修饰静态方法,是对类进行加锁(Class对象),如果该类中有methodA和methodB都是被Synch修饰的静态方法,此时有两个线程T1、T2分别调用methodA()和methodB()&#x…...

LLaMA Factory多卡微调的实战教程(持续更新)
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...

IOUtils的妙用
查看IOUtils的api文档,它的方法大部分都是重载的,方法的用法总结如下: 方法名使用说明buffer将传入的流进行包装,变成缓冲流。并可以通过参数指定缓冲大小closeQueitly关闭流contentEquals比较两个流中的内容的是否一致copy将输入…...

目标检测——室内服务机器人LifelongSLAM数据集
引言 亲爱的读者们,您是否在寻找某个特定的数据集,用于研究或项目实践?欢迎您在评论区留言,或者通过公众号私信告诉我,您想要的数据集的类型主题。小编会竭尽全力为您寻找,并在找到后第一时间与您分享。 …...
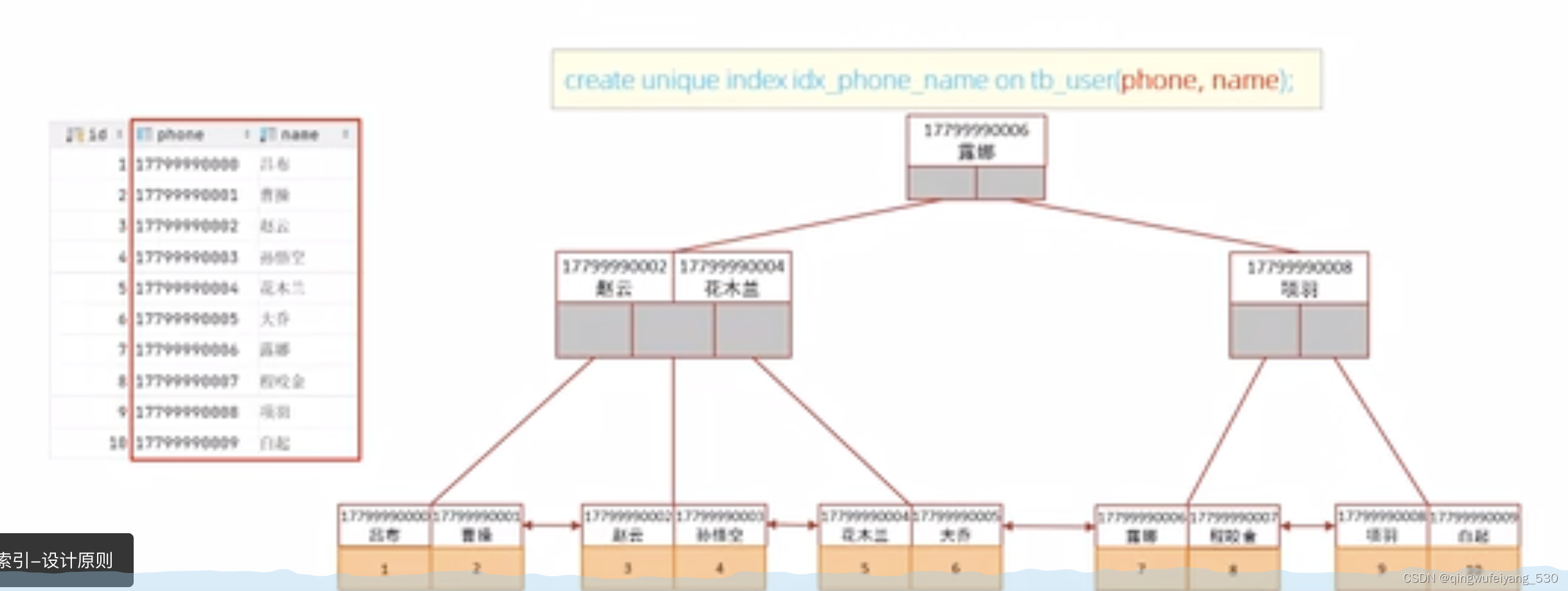
Mysql学习笔记-进阶篇
一、存储引擎 1、MYSQL体系结构 连接层、服务层、引擎层、存储层; 2、存储引擎简介 存储引擎就是存储数据、建立索引、更新/查询数据等技术的实现方式。存储引擎是基于表的,而不是库的,所以存储引擎也可被称为表类型。 1)在创…...

AI写真:ControlNet 之 InstantID
但是 IPAdapter-FaceId 目前只在 SD 1.5 模型上表现较好,SDXL 模型上的表现较差,不能用于实际生产。可是很多同学已经在使用SDXL了,而且SDXL确实整体上出图效果更好,怎么办? 这篇文章就来给大家介绍一个在SDXL中创作A…...

单元测试的思考与实践
1. 什么是单元测试 通常来说单元测试,是一种自动化测试,同时包含一下特性: 验证很小的一段代码(业务意义 或者 代码逻辑 上不可再分割的单元),能够更准确的定位到问题代码的位置 能够快速运行(…...

C# Socket通讯简单Demo
C# Socket通讯简单Demo Client端Listener端 Client端 static void Main(string[] args) {XSocketService XSocketService new XSocketService();XSocketService.Init();while (true){Console.Write("请输入消息:");var msg Console.ReadLine();XSocket…...

视频融合共享平台LntonCVS视频监控管理平台技术方案详细介绍
LntonCVS国标视频综合管理平台是一款以视频为核心的智慧物联应用平台。它基于分布式、负载均衡等流媒体技术进行开发,提供广泛兼容、安全可靠、开放共享的视频综合服务。该平台具备多种功能,包括视频直播、录像、回放、检索、云存储、告警上报、语音对讲…...

C#ListView的单元格支持添加基本及自定义任意控件
功能说明 使用ListView时,希望可以在单元格显示图片或其他控件,发现原生的ListView不支持,于是通过拓展,实现ListView可以显示任意控件的功能,效果如下: 实现方法 本来想着在单元格里面实现控件的自绘的…...
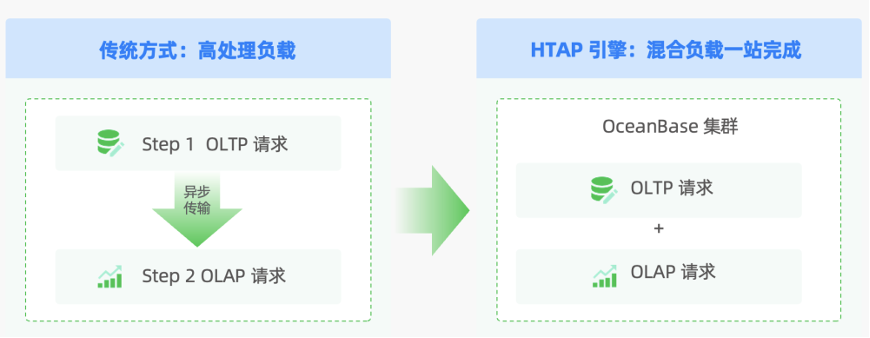
数据库选型实践:如何避开分库分表痛点 | OceanBase用户实践
随着企业业务的不断发展,数据量往往呈现出快速的增长趋势。使用MySQL的用户面对这种增长,普遍选择采用分库分表技术作为应对方案。然而,这一方案常在后期会遇到很多痛点。 分库分表的痛点 痛点 1:难以保证数据一致性。由于分库分…...

3个火火火的AI项目,开源了!
友友们,今天我要给你们安利三个超酷的开源项目,它们都和AI有关,而且每一个都能让你的日常生活变得更加有趣和便捷!(最近AI绘图又又超神了,分享以下美图养眼) 01 字节出品,文字转语音Seed-TTS 字节推出了一…...

算法 | 子集数排列树满m叉树二分搜索归并排序快速排序
子集树:O(2^n) 一个序列的所有子集为2^n,即可看成具有2^n个叶节点的满二叉树 int backtrack(int k) //k表示扩展结点在解空间树中所处的层次 {if(k>n) //n标识问题的规模output(x); //x是存放当前解的一维数组if(constraint(k)…...

SpringBoot配置第三方专业缓存技术jetcache方法缓存方案
jetcache方法缓存 我们可以给每个方法配置缓存方案 JetCache 是一个基于 Java 的缓存库,支持多种缓存方案和缓存策略,主要用于提升应用程序的性能和响应速度。它提供了多种缓存模式和特性,可以根据需求选择合适的缓存方案。 JetCache 的主…...
游戏开发丨基于PyGame的消消乐小游戏
文章目录 写在前面PyGame消消乐注意事项系列文章写在后面 写在前面 本期内容:基于pygame实现喜羊羊与灰太狼版消消乐小游戏 下载地址:https://download.csdn.net/download/m0_68111267/88700193 实验环境 python3.11及以上pycharmpygame 安装pygame…...
软件项目管理概述
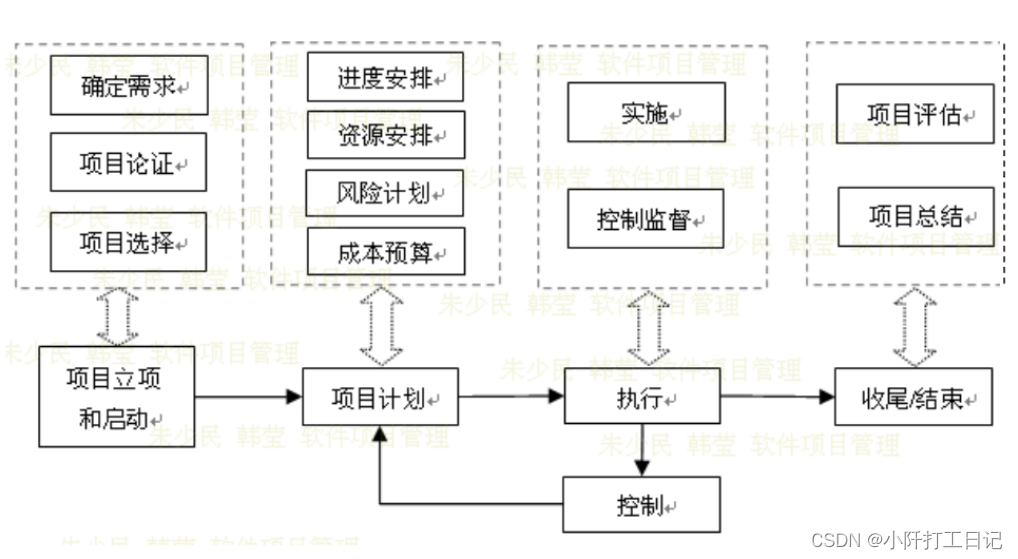
1.什么是项目? 2.项目管理的定义 3.项目管理的本质 4.项目成功的标志 5.项目管理的基本方法 6.项目的生命周期(启动 计划 执行 控制 结束) 7.结合生活中的某件事,谈谈项目管理的作用 项目管理在日常生活中扮演着重要的角色&…...

FastAdmin后台开发框架 lang 任意文件读取漏洞复现
0x01 产品简介 FastAdmin是一款基于PHPBootstrap的开源后台框架,专为开发者精心打造。它基于ThinkPHP和Bootstrap两大主流技术构建,拥有完善的权限管理系统和一键生成CRUD等强大功能。FastAdmin致力于提高开发效率,降低开发成本,…...

数字时代PLM系统的重要性
什么是 PLM(产品生命周期管理)? 从最基本的层面上讲,产品生命周期管理 (PLM)是管理产品从最初构思、开发、服务和处置的整个过程的战略流程。换句话说,PLM 意味着管理产品从诞生到消亡所涉及的一切。 什么是 PLM 软件…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
