【Java面试】二十、JVM篇(上):JVM结构
文章目录
- 1、JVM
- 2、程序计数器
- 3、堆
- 4、栈
- 4.1 垃圾回收是否涉及栈内存
- 4.2 栈内存分配越大越好吗
- 4.3 方法内的局部变量是否线程安全吗
- 4.4 栈内存溢出的情况
- 4.5 堆和栈的区别是什么
- 5、方法区
- 5.1 常量池
- 5.2 运行时常量池
- 6、直接内存
1、JVM
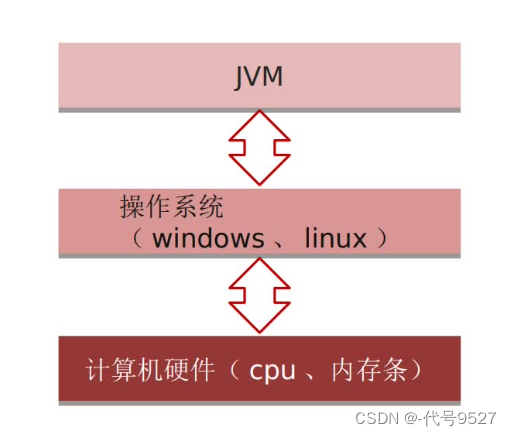
Java源码编译成class字节码后,JVM负责class字节码的处理。不同操作系统下的JVM,将字节码处理成对应操作系统下的二进制文件,从而实现一次编译,到处运行。能到处运行,是因为不同操作系统有不同的JVM,也即编译后的class字节码和操作系统之间,隔着一个JVM在干活儿。
简单的理解,JVM就是Java二进制字节码的运行环境,是JDK包下包含的一些代码,像一个虚拟的计算机一样处理着class字节码。
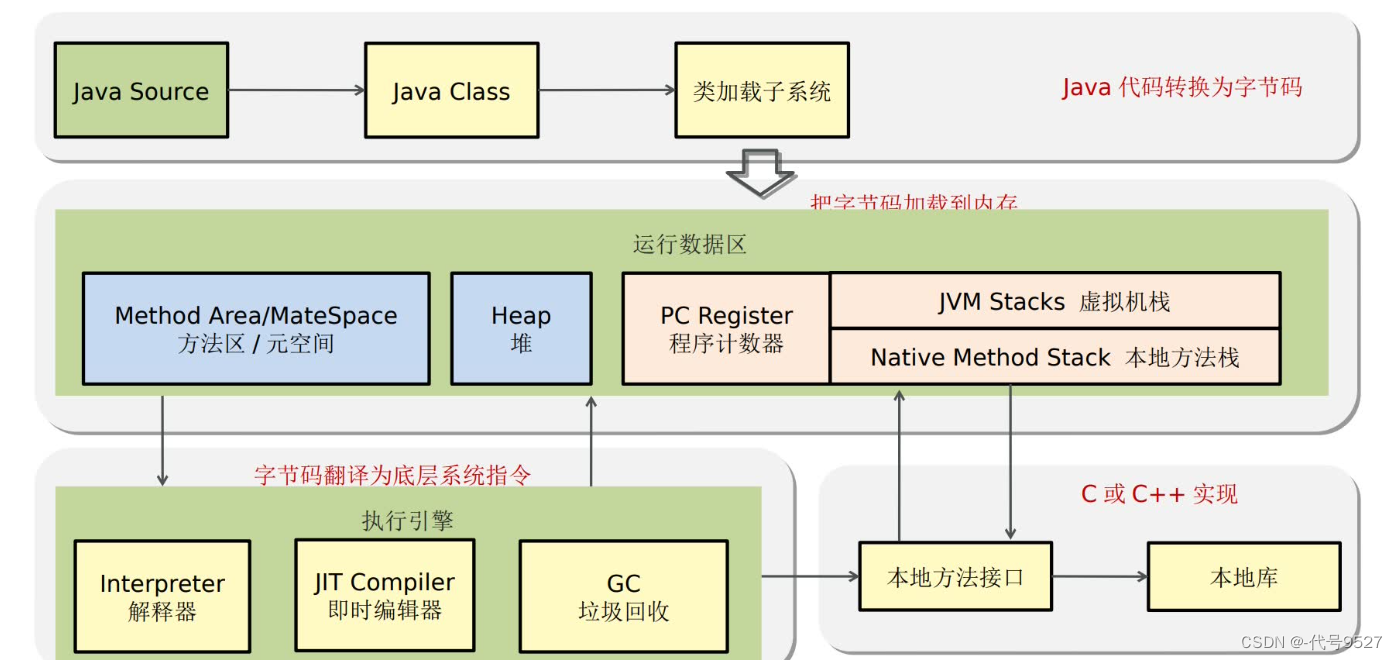
JVM有两个最大的亮点:
- 处理class字节码,实现一次编译,到处运行
- 自动内存管理,垃圾回收机制,创建的对象,用完后不用手动回收
JVM的组成:
2、程序计数器
线程私有的,每个线程各有一份,内部保存的字节码的行号。用于记录正在执行的字节码指令的地址。

如上,线程1 执行字节码从第0行到第10行后,CPU时间片用完,线程1的程序计数器记录下当前行号。CPU的时间片分给了线程2 ,线程2执行到第9行后,CPU时间片用完。线程1再次抢到时间片,继续执行,此时,根据线程1的程序计数器,CPU就知道该从第10行继续往下执行。
3、堆
- 堆区,线程共享
- 保存着创建出来的对象
- use、total、max,use == max 后,无法再分配空间,堆内存溢出
堆中有年轻代和老年代。年轻代有三部分,伊甸园区和两块大小相同的幸存者区。根据JVM策略,新创建的对象在伊甸园区,伊甸园区满了以后,触发Young GC,GC后或者的对象,复制到幸存者区,后面每GC一次,活着的对象年龄加一(对象头里存着年龄),对象GC年龄到达阈值(如15)后,晋升到老年代。
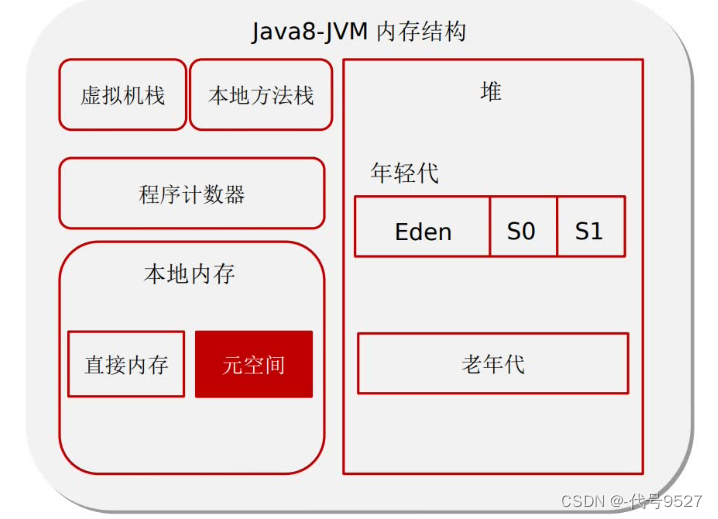
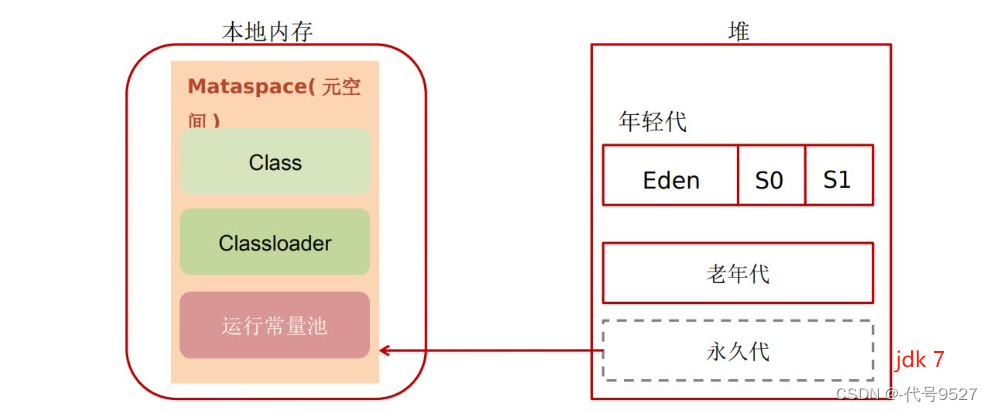
元空间里存类的信息、静态变量、常量、编译后的字节码信息(InstanceKlass对象(c++))。对JDK7和8,其位置变化:
- JDK7及以前,方法区在堆区的永久代空间里
- JDK8及以后,永久代被移除,用元空间代替,方法区在元空间,而元空间在操作系统的直接内存里,理论上可以一直分配
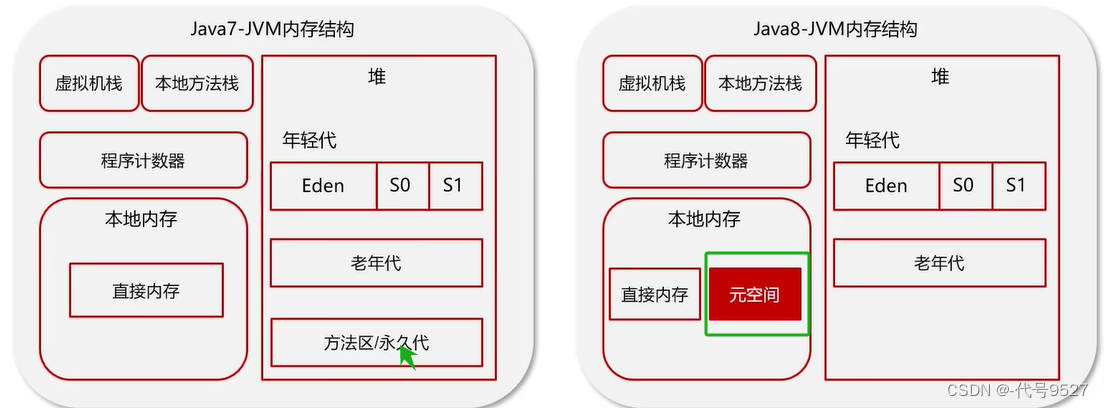
因为永久代/方法区或者说后来的元空间,存储的主要是一些类信息和常量,需求开发,加载的类越来越多,这个空间不可控,移除永久代,在本地内存放个元空间,可以防止OOM
4、栈
栈,即每个线程运行时需要的内存空间,保存着该线程方法调用的基本数据,先进后出,其中,每一个调用的方法用一个叫栈帧的东西存。
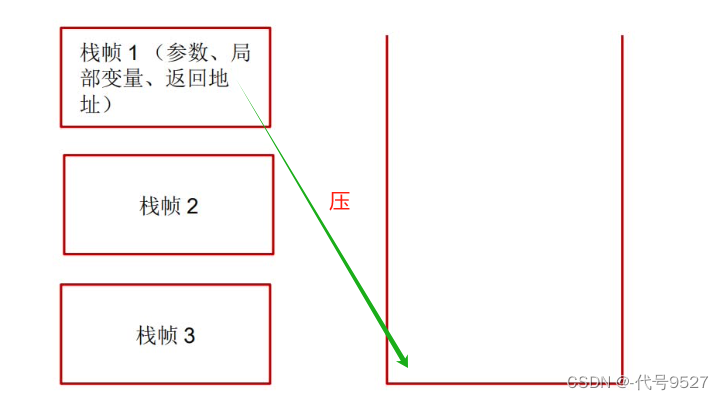
4.1 垃圾回收是否涉及栈内存
垃圾回收处理的主要是堆内存,对于栈内存,栈帧弹栈后,内存就会释放
4.2 栈内存分配越大越好吗
默认1024k,栈帧过大会导致线程数变少,机器总内存为512m,目前能活动的线程数则为512个,如果把内存改为2048k,则可活动的线程数上限在栈内存方面就会减半
4.3 方法内的局部变量是否线程安全吗
在方法的作用范围之内,是线程安全的。出了方法,被怎么使用就不一定了。如下:

每个线程过来,都会在自己的栈里创建一个m1方法对应的栈帧,栈帧里存着局部变量sb,因此线程安全。
对m2方法来说,局部变量sb是传过来的,那可能就有线程安全问题,如上面main线程中在操作sb,新开的一个线程也在操作sb。同理,m3方法,将局部变量sb return,后面可能被一个成员变量接收,但后面本质上也不关局部变量的事了
4.4 栈内存溢出的情况
- 栈帧过多导致栈内存溢出,如递归调用
public static void m1() {m1();
}
- 栈帧过大导致栈内存溢出
4.5 堆和栈的区别是什么
- 栈内存一般会用来存储局部变量和方法调用,但堆内存是用来存储Java对象和数组的
- 堆会GC垃圾回收,而栈不会
- 栈内存是线程私有的,而堆内存是线程共有的
- 两者异常错误不同,但如果栈内存或者堆内存不足都会抛出异常,栈空间不足:Java.ang.StackOverFlowError,堆空间不足:java.lang.OutOfMemoryError.
5、方法区
- 方法区和堆一样,各个线程共享
- 主要存储类的信息(InstanceKclass对象)、运行时常量池
- 虚拟机启动的时候创建,虚拟机关闭的时候释放
- 方法区的内存空间不够时,抛异常OutOfMemoryError:Metaspace
- 方法区是一个概念,不同版本的JDK有不同的实现,对JDK7来说,永久代是其对方法区的落地实现(且此时永久代在堆区),对JDK8来说,则给方法区换了一种实现:元空间(元空间在本地内存)
5.1 常量池
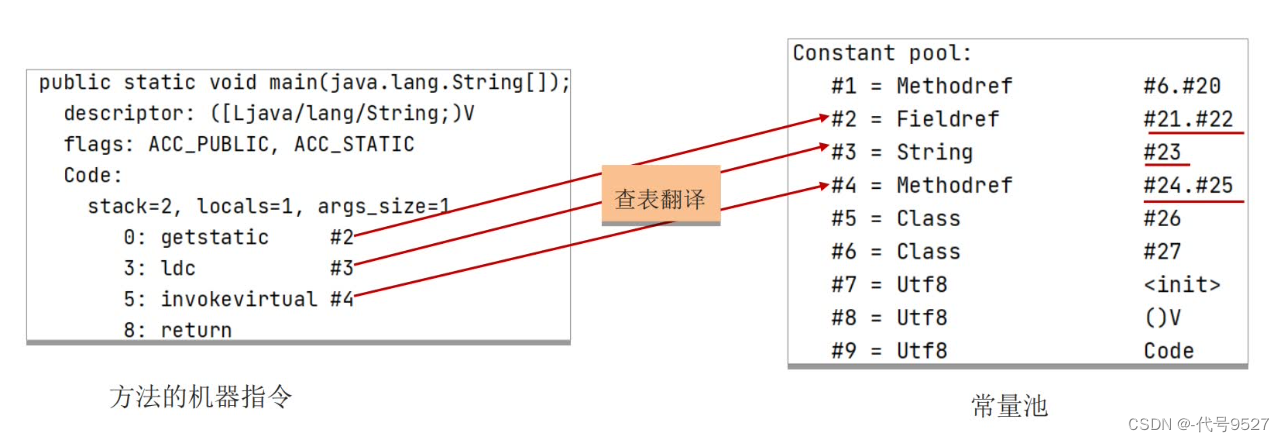
javap查看一个类是字节码的结构信息:可以看到类的基本信息、常量池、方法的定义:

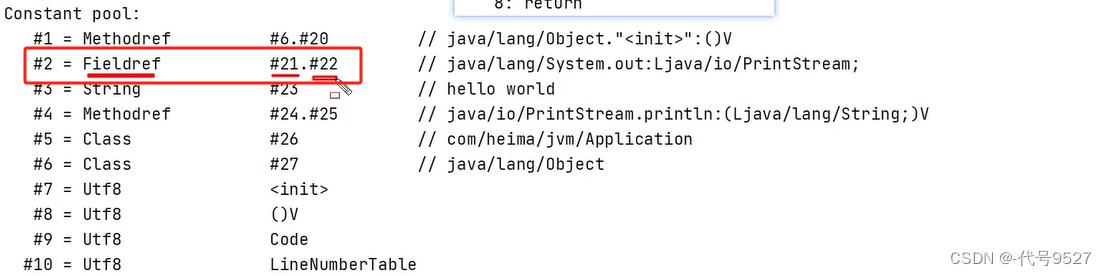
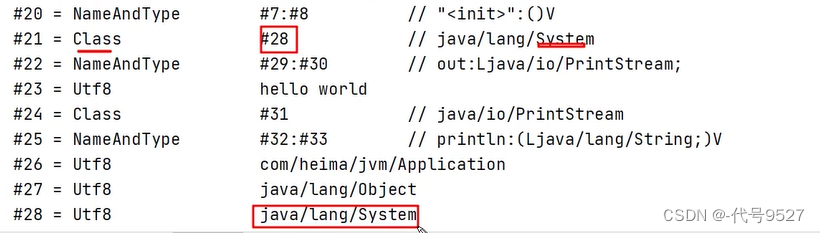
常量池可以看作是一张表,虚拟机指令根据这张常量表找到要执行的类名、方法名、参数类型、字面量等信息
5.2 运行时常量池
上面提到,常量池是class文件中的,当这个类被加载,它的常量池信息就会放入到运行时常量池,并发里面的符号地址变为真实地址
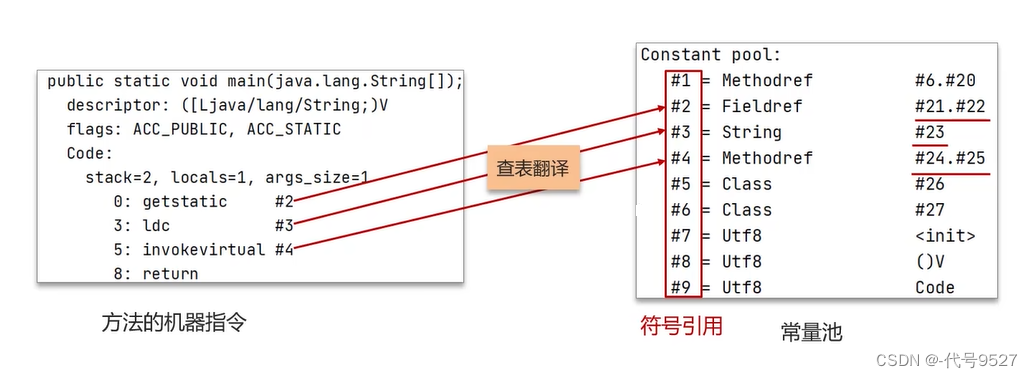
常量池和运行时常量池的区别:

【区别】
6、直接内存
直接内存(操作系统分给JVM进程的内存之外的内存),不属于JVM内存,不由JVM进行管理。在进行NIO操作时,用于数据缓冲区,其分配回收成本高,但读写性能好。常规IO复制文件流程:
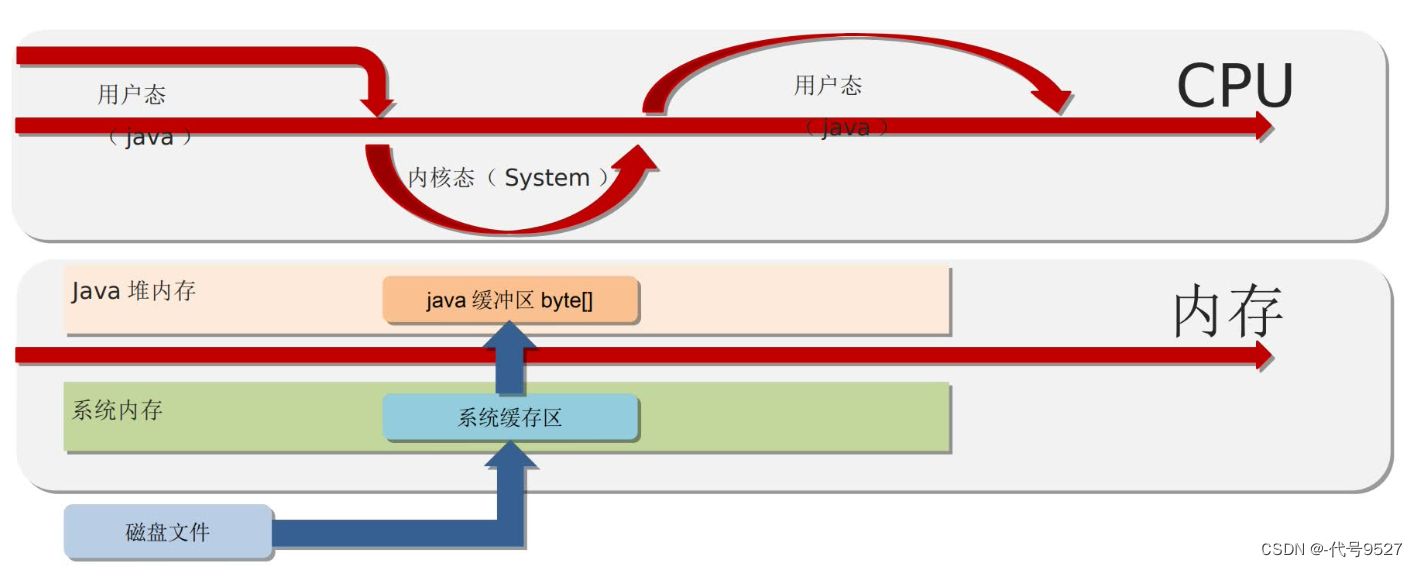
NIO复制文件流程:这块直接内存系统和Java代码都可以直接访问,少了一次缓冲区的复制操作

直接内存主要通过 java.nio 包下的 ByteBuffer 类来进行分配和使用。
ByteBuffer.allocateDirect(int capacity)
直接内存可以减少数据在 Java 堆和操作系统内存之间的拷贝次数,从而提高 I/O 的效率,常用于文件读写
【相关】
相关文章:

【Java面试】二十、JVM篇(上):JVM结构
文章目录 1、JVM2、程序计数器3、堆4、栈4.1 垃圾回收是否涉及栈内存4.2 栈内存分配越大越好吗4.3 方法内的局部变量是否线程安全吗4.4 栈内存溢出的情况4.5 堆和栈的区别是什么 5、方法区5.1 常量池5.2 运行时常量池 6、直接内存 1、JVM Java源码编译成class字节码后…...

【Python教程】压缩PDF文件大小
压缩 PDF 文件能有效减小文件大小并提高文件传输的效率,同时还能节省计算机存储空间。除了使用一些专业工具对PDF文件进行压缩,我们还可以通过 Python 来执行该操作,实现自动化、批量处理PDF文件。 本文将分享一个简单有效的使用 Python 压缩…...
UE4中性能优化和检测工具
UE4中性能优化和检测工具合集 简述CPUUnreal InsightUnreal ProfilerSimpleperfAndroid StudioPerfettoXCode TimeprofilerBest Practice GPUAdreno GPUMali GPUAndroid GPU Inspector (AGI) 内存堆内存分析Android StudioLoliProfilerUE5 Memory InsightsUnity Mono 内存Memre…...

大型ERP设计-业务与功能指引:外币折算与辅助账套
外币折算与辅助账套 前言:在对ORACLE和SAP的核心模块功能全面解读的基础上,给出大型ERP设计的建议-业务与功能指引,企业选型、开发大型ERP软件的公司和ERP顾问可以参考。模块包括财务、计划与制造、供应链、项目及设备(MRO),初步预…...
重学java 73.设计模式
本想送你一本沉思录,可该迷途知返的人是我 —— 24.6.18 设计模式 设计模式(Design pattern),是一套被反复使用、经过分类编目的、代码设计经验的总结,使用设计模式是为了可重用代码、保证代码可靠性、程序的重用性,稳定性。 1995 年&#x…...

线代的学习(矩阵)
1.矩阵的乘法 矩阵实现满足:内标相等 矩阵相乘之后的结果:前行后列 需要注意:1.矩阵的乘法不具有交换律:AB!BA 2.矩阵的乘法满足分配律:A(BC) AB AC 抽象逆矩阵求逆矩阵 方法1.凑定义法、 方法2.长除法 数字型矩阵…...

【Java基础5】JDK、JRE和JVM的区别与联系
JDK、JRE和JVM的区别与联系 Java是一种广泛使用的编程语言,它的跨平台特性得益于Java虚拟机(JVM)。然而,在Java的世界里,JDK、JRE和JVM这三个术语常常让人感到困惑。本文将阐述它们各自的功能,以及它们是如…...

2024年先进机械电子、电气工程与自动化国际学术会议(ICAMEEA 2024)
2024年先进机械电子、电气工程与自动化国际学术会议(ICAMEEA 2024) 2024 International Conference on Advanced Mechatronic, Electrical Engineering and Automation 会议地点:杭州,中国 网址:www.icameea.com 邮箱: icameeasub-conf.c…...

WPF 深入理解四、样式
样式 WPF中的各类控件元素,都可以自由的设置其样式。 诸如: 字体(FontFamily) 字体大小(FontSize) 背景颜色(Background) 字体颜色(Foreground) 边距(Margin) 水平位置(HorizontalAlignment) 垂直位置(VerticalAlignment)等等。 而样式则是组织和重用以上的重要工具。不是使…...
TCP相关细节
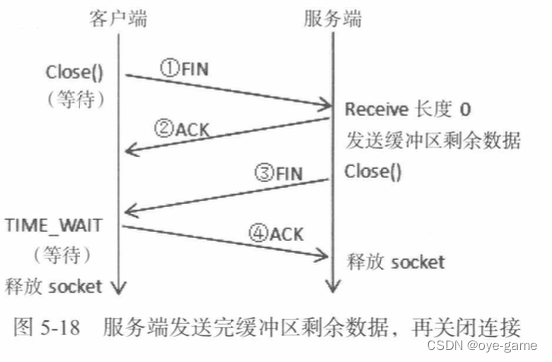
1. 常用TCP参数 1.1 ReceiveBufferSize ReceiveBuffersize指定了操作系统读缓冲区的大小, 默认值是8192(如图5-10 所示)。在第4章的例子中,会有"假设操作系统缓冲区的长度是8" 这样的描述,可通过socket.ReceiveBufferSize 8 实现。当接收端缓冲区满了的时…...

flutter实现UDP发送魔法包唤醒主机
魔法包 魔法包是用16进制表示的数据包,它是由固定的前缀数据(FFFFFFFFFFFF)以及固定重复次数(16次)的目标主机MAC地址组成。 假设目标主机的MAC地址是:"50:eb:f6:27:ae:a8" 那么魔法包就是[FFFFFFFFFFFF50EBF627AEA850EBF627AEA850EBF627AEA8…...

回溯算法练习题(2024/6/18)
1全排列 II 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2: 输入:nums [1,2,3] 输出:[[1,…...
DSP——从入门到放弃系列2——PLL锁相环(持续更新)
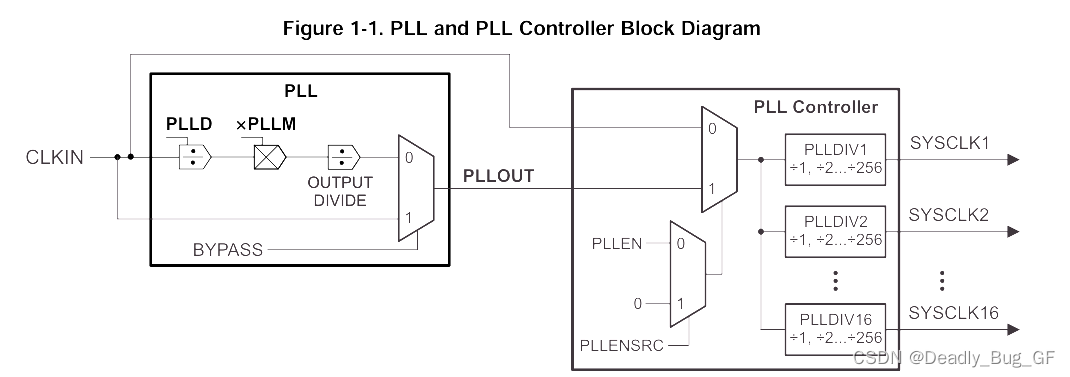
1、概述 锁相环(Phase Locked Loop,PLL)是处理器的时钟源,控制着C6678处理器中C66x内核、各外围设备的时钟的时钟比、对准和选通功能。 2、功能描述 上图显示了PLL和PLL控制器的逻辑实现。PLL控制器提供通过软件可配置的分频器࿰…...

Altair 人工智能技术助力MABE预测消费者行为,实现设备性能优化
主要看点 行业: 家电行业 挑战: 企业面临的挑战是如何利用已收集的大量数据,深入了解消费者在产品使用过程中对某些保鲜程序的影响。 Altair 解决方案: Altair采用了Altair RapidMiner人工智能平台来解决问题,特别是…...

解决Spring Boot项目中数据源URL属性的问题
今天测试Springboot项目的时候,报错: . ____ _ __ _ _/\\ / ____ __ _ _(_)_ __ __ _ \ \ \ \ ( ( )\___ | _ | _| | _ \/ _ | \ \ \ \\\/ ___)| |_)| | | | | || (_| | ) ) ) ) |____| .__|_| |_|_| |_\__, | / / / /|_||___…...

Java每日作业day6.18
ok了家人们今天我们继续学习方法的更多使用,闲话少叙,我们来看今天学了什么 1.重载 在同一个类中,可不可以存在同名的方法?重载:在同一个类中,定义了多个同名的方法,但每个方法具有不同的参数类型或参数个…...
mac如何检测硬盘损坏 常用mac硬盘检测坏道工具推荐
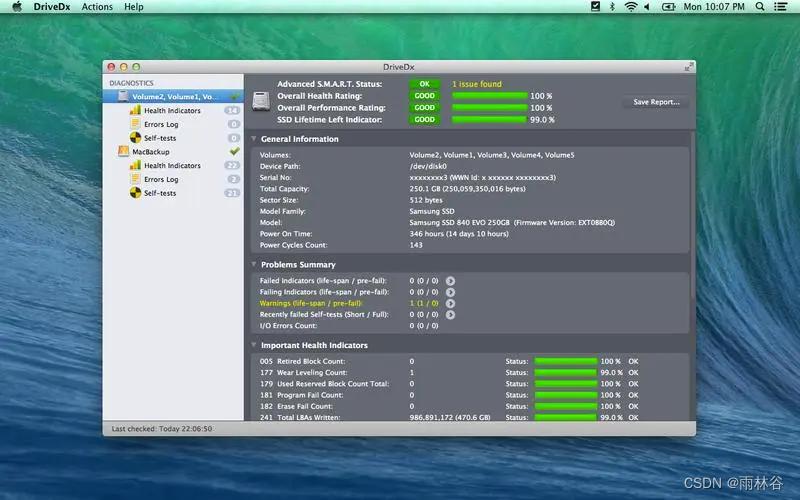
mac有时候也出现一些问题,比如硬盘损坏。硬盘损坏会导致数据丢失、系统崩溃、性能下降等严重的后果,所以及时检测和修复硬盘损坏是非常必要的。那么,mac如何检测硬盘损坏呢?有哪些常用的mac硬盘检测坏道工具呢? 一、m…...

怎么通俗理解概率论中的c r(cramer rao 克拉默拉奥)不等式?
还是推一下比较好记 视频链接 【数理统计学重要定理证明:C-R不等式——无偏估计的方差下界-哔哩哔哩】 https://b23.tv/4gk1AvU 【数理统计学重要定理证明:C-R不等式——无偏估计的方差下界-哔哩哔哩】...

Flask之模板
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 目录 一、模板的基本用法 1.1、创建模板 1.2、模板语法 1.3、渲染模板 二、模板辅助工具 2.1、上下文 2.2、全局对象 2.3、过滤器 2.4、测试…...

如何优化 Bash 脚本的执行效率?
要优化 Bash 脚本的执行效率,可以考虑以下几个方面: 减少命令执行次数:Bash 脚本中的命令执行是比较耗时的,在可能的情况下,可以尽量减少命令的执行次数。例如,可以将多个命令合并成一个,使用管…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
