求“二维随机变量的期望E(X)与方差D(X)”例题(一)
离散型
设随机变量(X,Y)的联合分布律为
| X\Y | 0 | 1 |
|---|---|---|
| 0 | 0.1 | 0.2 |
| 1 | 0.3 | 0.4 |
(1)求E(X)
先求x的边缘分布律,表格里x=0的概率为0.1+0.2,于是我们可得
| X | 0 | 1 |
|---|---|---|
| P | 0.3 | 0.7 |
直接求E(X)即可,得到结果
(2)求E(XY)
直接x与y相乘就行。
记得别乘多了,别的算了又算遍
。
(3)求E(X+Y)
和上面一样,x与y相加就行。
连续型
已知随机变量(X,Y)的概率密度。
(1)求E(X)
和求一维连续型随机变量的步骤差不多。把E(X)的x当作g(x),然后求个这个二重积分即可。
由于函数在除了[0,1]的区间上都为0,对其积分也为0。同时x和y的上下限都已经给出。我们可以得到。
关于二重积分的相关知识在高数下。这里作简述:这里的二重积分是化成了x型。也就是把dx往前提;然后先写x的取值范围再写y的取值范围。由于x是自变量所以上下限应与y无关。所以这里是[0,1]而不是[y,1]。而y是因变量,所以上下限为[0,x]。所要求的式子与dy放在一起。然后就变成了求解定积分--先求对y的积分,再对得出来的结果求x的积分。
运算过程太多,这里写关键的。即
(2)求E(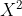 )
)
求步骤和上面一样,只不是是g(x)=
,所以式子变成了
上下限没变,计算方法没变。这里就直接放结果为
(3)求E(XY)
还是和上面一样的,式子变成了,结果为
相关文章:
求“二维随机变量的期望E(X)与方差D(X)”例题(一)
离散型 设随机变量(X,Y)的联合分布律为 X\Y0100.10.210.30.4 (1)求E(X) 先求x的边缘分布律,表格里x0的概率为0.10.2,于是我们可得 X01P0.30.7直接求E(X)即可,得到结果 (2)求E(XY) 直接x与y相乘就行。 记得别乘多了,别的算了又…...
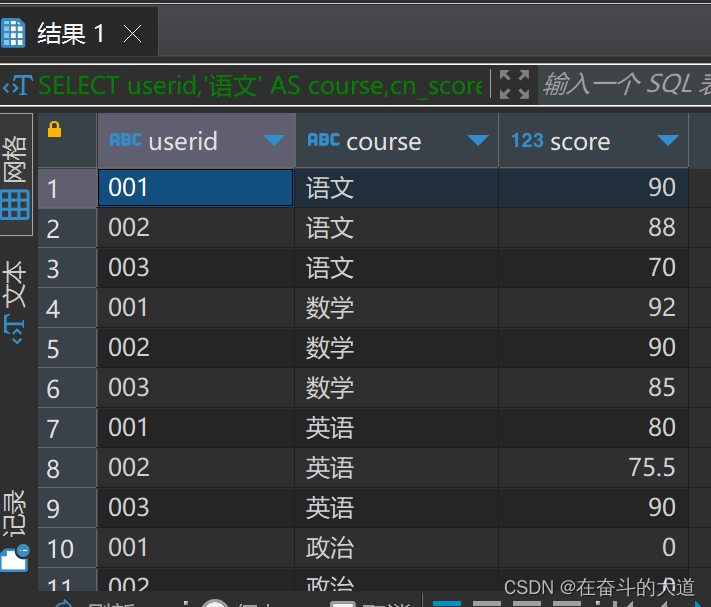
MySQL 搞定行转列,列转行
行转列方法总结1、使用case…when…then2、使用SUM(IF()) 生成列3、使用SUM(IF()) 生成列 WITH ROLLUP 生成汇总行4、使用SUM(IF()) 生成列 UNION 生成汇总行,并利用 IFNULL将汇总行标题显示为 Total5、使用SUM(IF()) 生成列,直接生成汇总结果,不再利用…...
正点原子裸机开发之C语言点灯程序
一. 简介 本文针对 IMX6ULL 的裸机开发的(即不带Linux操作系统的开发)。 主要分两部分的工作: 1. 配置 C语言运行环境 2. C 语言编写及运行 二. 配置C语言运行环境 配置 C 语言运行环境的工作分 三部分。如下: 1. 设置…...

cv::阈值分割OTUS原理+代码
opencv库的阈值分割分为全局分割和局部分割全局分割:普通分割ret1,th1 cv2.threshold(img,127, 255, cv2.THRESH_BINARY) #127为阈值 #cv2.THRESH_BINARY |cv2.THRESH_BINARY_INV | cv2.THRESH_TRUNC|cv2.THRESH_TOZERO|cv2.THRESH_TOZERO_INV局部分割:…...
Postgresql-12.5 visual studio-2022 windows 添加pg工程并调试
pg内核学习,记录一下 文章目录安装包编译安装VS添加Postgresql工程调试源码安装包 (1)perl下载 https://www.perl.org/get.html (2)diff下载 http://gnuwin32.sourceforge.net/packages/diffutils.htm (…...

长沙学院2023 第一次蓝桥训练题解
每道题都在洛谷上,每个题都有很详细的题解,可以先自行做,不会再看题解。 题目解析思路都写在代码中,中文题面就不单独解释题意了。 P2440 木材加工(二分答案) 链接:P2440 木材加工 解析 代码…...

云端Docker搭建ABY库以及本地CLion使用
文章目录ABY的搭建以及使用前言ABY库的下载、安装及测试CLion配置后续杂项项目改名使用其他的库最后ABY的搭建以及使用 前言 仅做记录,仅供参考,不同人有不同的使用方式命令手敲,可能有错,自己辨识勿问,我懂的也不多…...

ES6-箭头函数、解构赋值、对象简写
箭头函数特点 1、 (只有1个形参) 可以省略() 2、 {} 可以省略 只有一句代码 或 只有返回值的时候,省略return 3、arguments 不可用,arguments在没有形参的时候可以拿到调用函数拿在的实参 获取伪数组通过Array.from转为真数组。 4、 箭头函数没有this, …...
【CSS】CSS 背景设置 ② ( 背景位置 | 背景位置-方位值设置 )
文章目录一、背景位置1、语法说明2、注意事项二、背景位置-方位值设置1、效果展示2、完整代码示例一、背景位置 1、语法说明 如果 盒子的大小 大于 背景图片的大小 , 默认的 图片 位置是 左上角 ; 设置背景位置的 CSS 语法如下 : background-position : length length backgro…...

HTML 扫盲
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录前言HTML 结构快速生成代码框架HTML 常见标签注释标签标题标签: h1-h6段落标签:p换行标签:br格式化标签…...

项目中用到的责任链模式
目录 1.什么是责任链?它的原理是什么? 2.应用场景 3.项目中的应用 传送门:策略模式,工作中你用上了吗? 1.什么是责任链?它的原理是什么? 将请求的发送和接收解耦,让多个接收对象…...

C++复习笔记--STL的string容器和vector容器
1--string容器string 本质上是一个类,其不同于指针 char*,string 类的内部封装了 char*,用于管理字符串,是一个 char* 型的容器;1-1--string构造函数string 的构造函数原型:string(); // 创建一个空的字符串…...
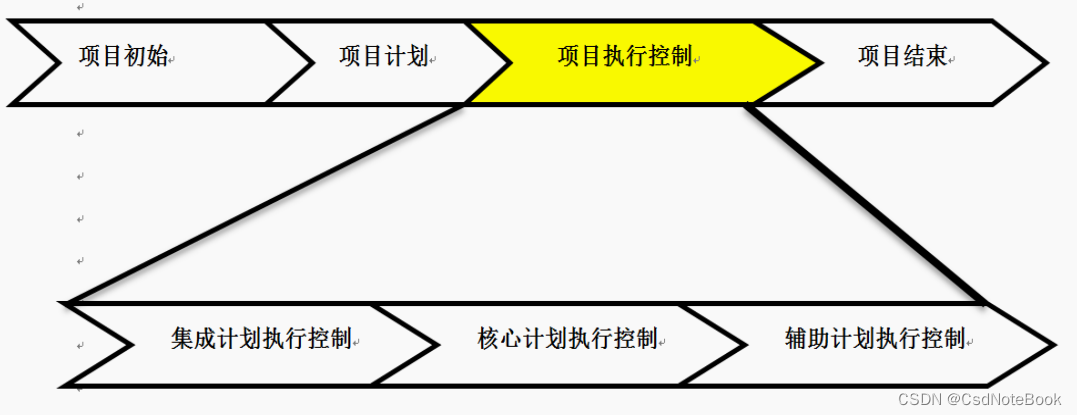
第一章 软件项目管理概述
项目(Project)是为了创造一个唯一的产品或提供一个唯一的服务而进行的临时性的努力。项目的特征PMBOK(A guide to the Project management Body Of Knowledge:项目管理知识体系指南)五大过程组和十大知识领域从时间角度出发,项目管理分为五大过程组:启动…...
【Linux系统编程】06:共享内存
共享内存 OVERVIEW共享内存一、文件上锁flock二、共享内存1.关联共享内存ftok2.获取共享内存shmget3.绑定共享内存shmat4.绑定分离shmdt5.控制共享内存shmctl三、亲缘进程间通信1.共享内存写入与读取2.共享内存解绑与删除3.共享内存综合四、非亲缘进程间通信1.通过sleep同步2.通…...
【专项】112. 路径总和
112. 路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点 …...
【数据结构】堆排序
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。大堆:每个节点的值都大于或者等于他的左右孩子节点的值小堆:每个结点的值都小于或等于其左孩子和右孩子结点…...
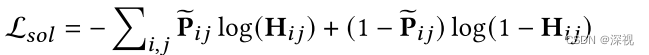
论文阅读笔记《GAMnet: Robust Feature Matching via Graph Adversarial-Matching Network》
核心思想 本文提出一种基于图对抗神经网络的图匹配算法(GAMnet),使用图神经网络作为生成器分别生成源图和目标图的节点的特征,并用一个多层感知机作为辨别器来区分两个特征是否来自同一个图,通过对抗训练的办法提高生成器特征提取…...

数据安全—数据完整性校验
1、数据安全保障三要素即 保密性 完整性、可用性机密性:要求数据不被他人轻易获取,需要进行数据加密。完整性:要求数据不被他人随意修改,需要进行签名技术可用性:要求服务不被他人恶意攻击,需要进行数据校验…...
Java 最小路径和
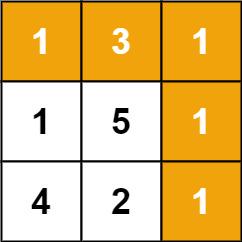
最小路径和中等给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。示例 1:输入:grid [[1,3,1],[1,5,1],[4,2,1]]输出&…...
Flask+VUE前后端分离的登入注册系统实现
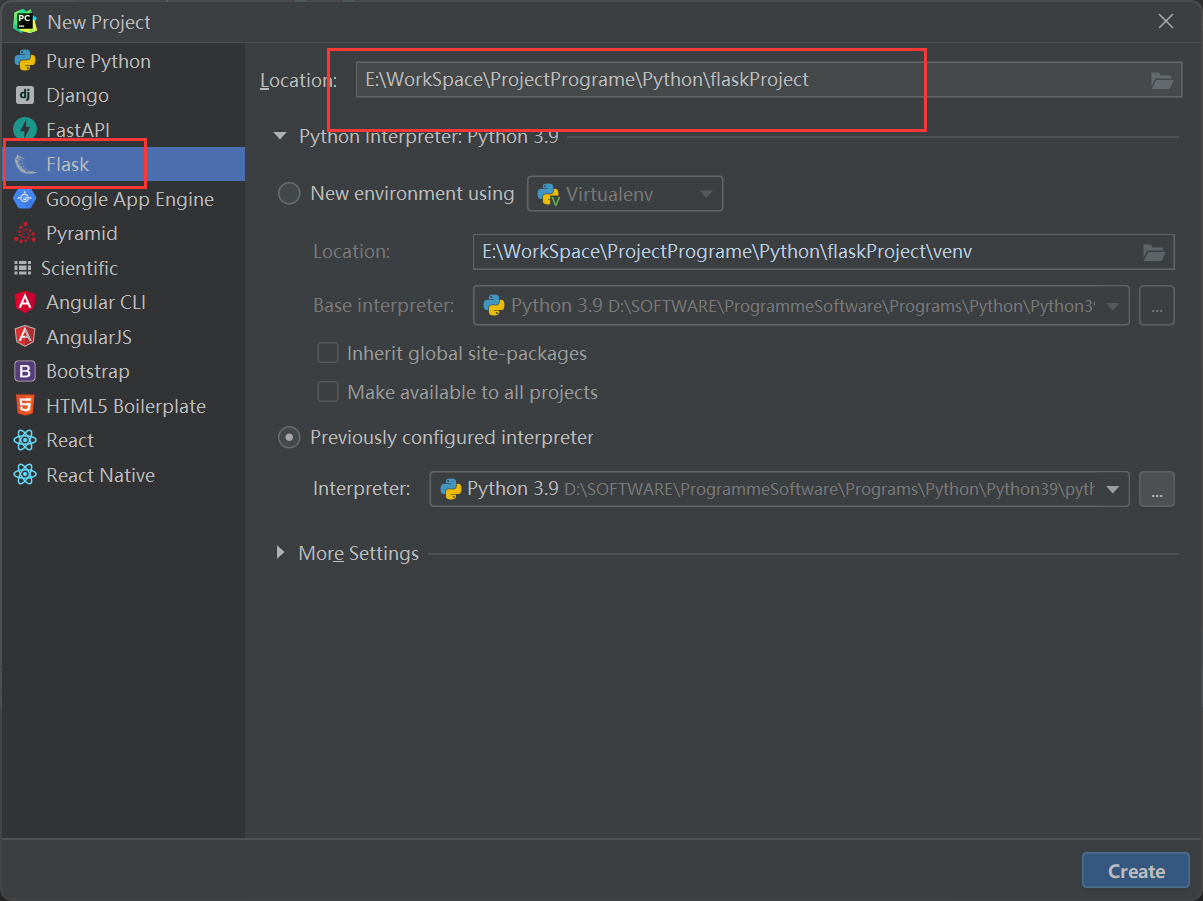
首先Pycharm创建一个Flask项目: Flask连接数据库需要下载的包: pip install -U flask-cors pip install flask-sqlalchemy Flask 连接和操作Mysql数据库 - 王滚滚啊 - 博客园 (cnblogs.com) sqlAlchemy基本使用 - 简书 (jianshu.com) FlaskVue前后端分…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
