代码随想录刷题-数组-有序数组的平方
文章目录
- 有序数组的平方
- 习题
- 暴力排序
- 双指针
有序数组的平方
本节对应代码随想录中:代码随想录,讲解视频:有序数组的平方_哔哩哔哩_bilibili
习题
题目链接:977. 有序数组的平方 - 力扣(LeetCode)
给你一个按非递减顺序排序的整数数组 nums,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
暴力排序
直接能想到的就是先把每个元素平方,然后再进行排序即可
class Solution {
public:vector<int> sortedSquares(vector<int>& A) {for (int i = 0; i < A.size(); i++) {A[i] *= A[i];}sort(A.begin(), A.end()); // 快速排序return A;}
};
双指针
首先来说一下为什么可以使用双指针
元素本来就是有序的,只不过因为里面有负数,负数平方后就可能大于某些正数的平方,从而顺序会发生变化
但是无论正数还是负数,其绝对值越大,那么它平方后也就会越大,即数组越靠近两边,平方后就会越大
那么我们就可以使用双指针,一个指向最左边,一个指向最右边。比较两边哪个平方后更大,存入新的数组中。然后更新指针,直到两个指针相遇,说明遍历完了所有的元素。
我的解法如下:
class Solution {public:vector<int> sortedSquares(vector<int>& nums) {int n = nums.size(), j = n - 1, k = n - 1;vector<int> copy = nums;for (int i = 0; i < n; i++,k--) {if (i == j) {nums[0] = copy[i] * copy[i];break;}if (copy[i] * copy[i] > copy[j] * copy[j]) {nums[k] = copy[i] * copy[i];} else {nums[k] = copy[j] * copy[j];j--;i--;} }return nums;}
};
看了别人的解法有几点可以注意下
vector<int> copy = nums;也可以写成vector<int> copy(nums.size(), 0);,区别是前者会复制 nums 的元素,而后者会将所有元素置0- for 循环中的
i<n可以i <= j;,这样就不用再用 if 判断相等时 break 了 - for 循环中的
i++,k--可以在 for 循环里面写,其实这样更符合逻辑,因为并不是每次都要i++,k--,只有满足特定情况时才会这样 - 不一定要用 for 循环,用
while(i<=j)来循环更符合逻辑
双指针思考:上一小节的移除元素中,两个指针都在最左边开始,只不过一个快点,一个慢点,快的用来遍历一遍元素,慢的用来指向满足条件的新的数组的下标;而这一节的双指针,一个在左边,一个在右边,两个指针不断比较,然后都往中间靠拢。上一小节的终止条件是快的指针遍历完一遍就停,而这一节的是当两个指针相遇时(i <= j;)停止
相关文章:

代码随想录刷题-数组-有序数组的平方
文章目录有序数组的平方习题暴力排序双指针有序数组的平方 本节对应代码随想录中:代码随想录,讲解视频:有序数组的平方_哔哩哔哩_bilibili 习题 题目链接:977. 有序数组的平方 - 力扣(LeetCode) 给你一…...
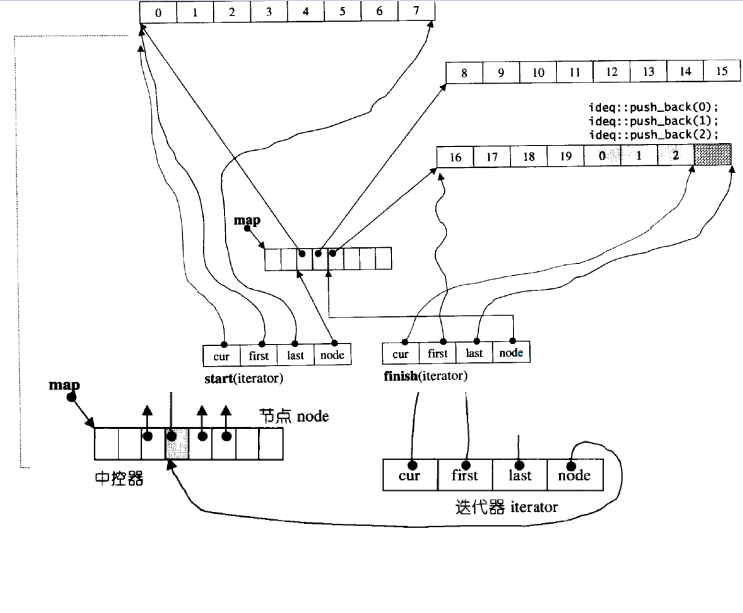
【玩转c++】stack和queue的介绍和模拟实现
本期主题:list的讲解和模拟实现博客主页: 小峰同学分享小编的在Linux中学习到的知识和遇到的问题小编的能力有限,出现错误希望大家不吝赐stack的介绍和使用1.1.stack的介绍1. stack是一种容器适配器,专门用在具有后进先出操作的上…...
Linux order(文件、磁盘、网络、系统管理、备份压缩)
1. Linux 文件命令 -rwxrwxrwx chmod:change mode,用于(文件所有者或 root )变更用户(u:owner g:group o:other a:all)的权限 chmod [OPTION]… MODE[,MODE]… FILE… OPTION -R:递归修改more option:chmod…...
最详细的CentOS7安装Mysql数据库服务
1.查看是否安装mysql: rpm -qa | grep mysql如果有查出来东西,使用命令删除: rpm -e xxx2.检查是否有mysql用户组和mysql用户,没有就添加有就忽略: groups mysql 添加用户组和用户 groupadd mysql && useradd -r -g mysql mysql&a…...
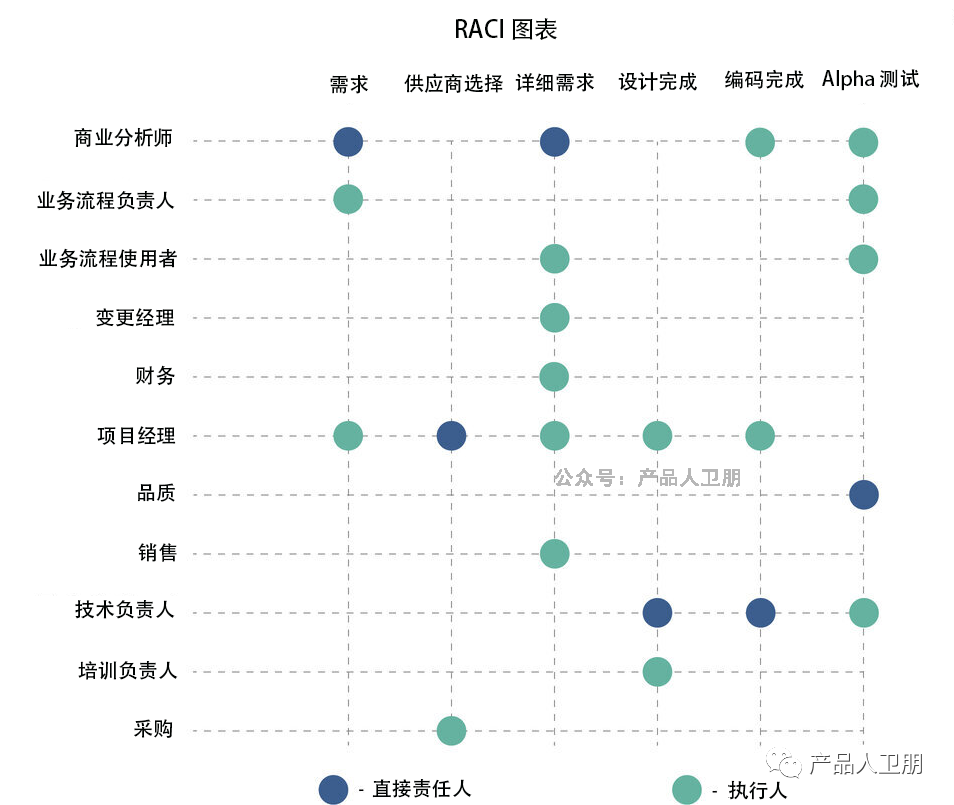
【IoT】项目管理:如何做好端到端的项目管理?
今天主要来谈谈项目管理这个话题。 首先来看一个我在网络上看到的一个关于项目管理的案例或者是段子。 将项目管理的作用及意义非常直观地展示了出来。 有一个植树搞绿化的企业,在公司内部设置有五个部门,分别是: 运输部门;挖坑部…...

渲染十万条数据就把你难住了?不存在的!
虚拟列表的使用场景如果我想要在网页中放大量的列表项,纯渲染的话,对于浏览器性能将会是个极大的挑战,会造成滚动卡顿,整体体验非常不好,主要有以下问题:页面等待时间极长,用户体验差CPU计算能力…...

编程学习的心路历程和困惑回顾
回首入行9年的经历,从大一开始学习C语言和数据结构,老师一直是在用IDE演示程序的编写和运行,我们也就一直在跟黑乎乎的命令行窗口打交道。 后来在一些课程的实验环节,接触到了一些别人编写好的工程代码,知道了Makefile…...
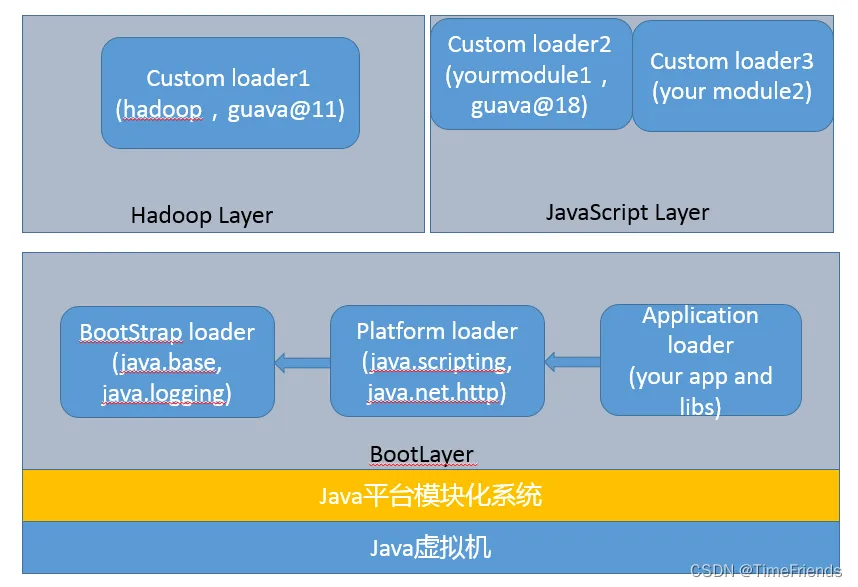
请介绍类加载过程,什么是双亲委派模型?
第23讲 | 请介绍类加载过程,什么是双亲委派模型? Java 通过引入字节码和 JVM 机制,提供了强大的跨平台能力,理解 Java 的类加载机制是深入 Java 开发的必要条件,也是个面试考察热点。 今天我要问你的问题是࿰…...
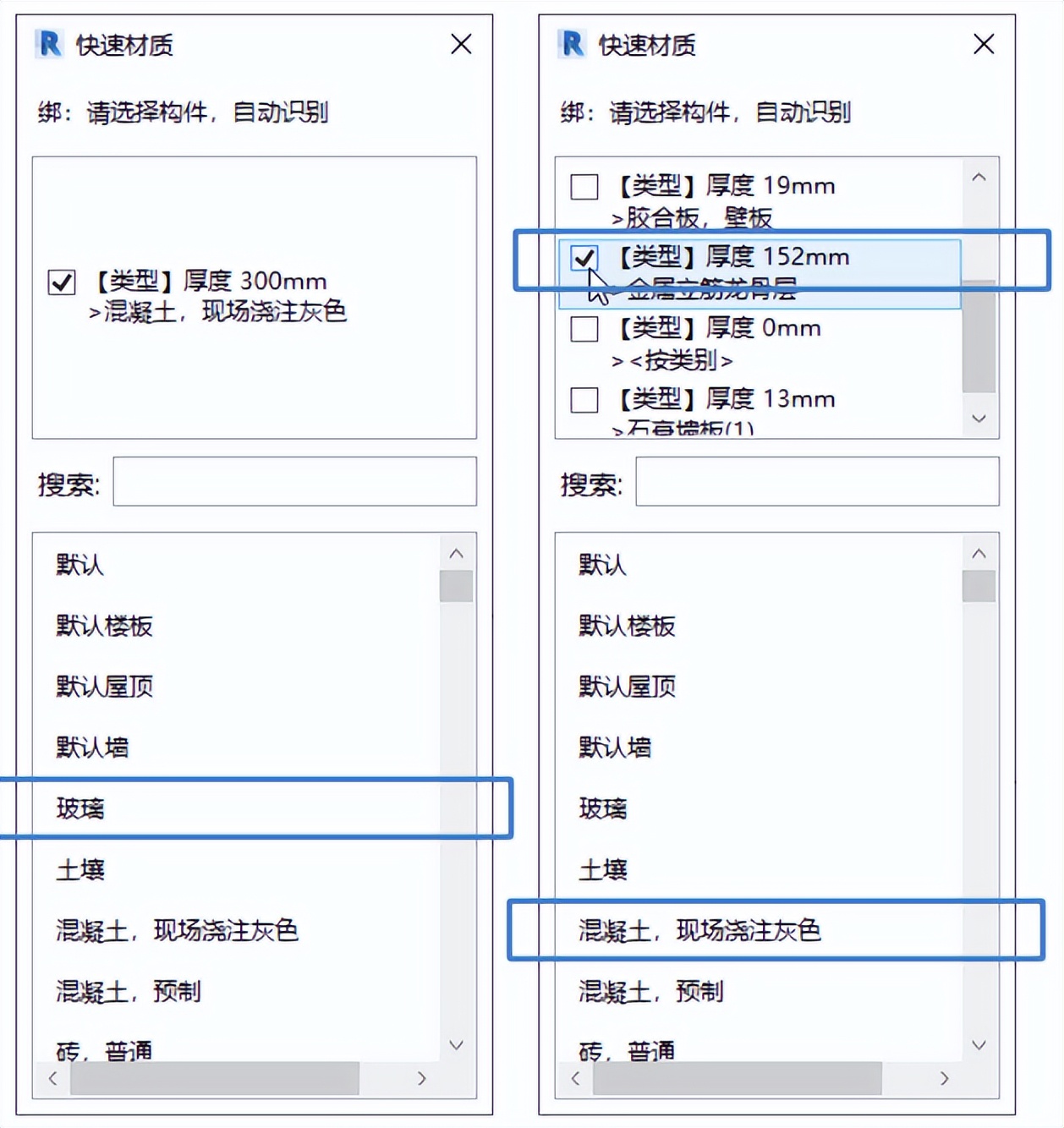
Navisworks编辑材质和Revit快速切换材质问题
一、如何在Navisworks2016中编辑材质 初次使用NW2016-2017时发现,原来用于创建编辑材质的小地球不见了,如图1所示,在各大技术群里求助没有回应,度娘搜索也总是摇头。 经过仔细排查可能出现的地方,终于找到了可以编辑材…...

Object对象键值的输出循序到底如何排列的?
1.日常摸鱼看八股 今天又是复习八股文的一天,发现还是彻底懂得原理才好和面试官吹牛批呀。 接着来看看我chat大宝贝的回答: 在现代浏览器中,Object 对象的键值输出循序是比较稳定的,通常是按照如下顺序输出: 所有的数…...

气泡式水位计的安装方法详解
气泡水位计的安装实际上就是气管的安装,气管的安装是否正确将直接影响到仪器测量数据的结果,气泡水位计它由活塞泵产生的压缩空气流经测量管和气泡室,进入被测的水体中,测量管中的静压力与气泡室上的水位高度成正比。那么接下来就…...
求“二维随机变量的期望E(X)与方差D(X)”例题(一)
离散型 设随机变量(X,Y)的联合分布律为 X\Y0100.10.210.30.4 (1)求E(X) 先求x的边缘分布律,表格里x0的概率为0.10.2,于是我们可得 X01P0.30.7直接求E(X)即可,得到结果 (2)求E(XY) 直接x与y相乘就行。 记得别乘多了,别的算了又…...
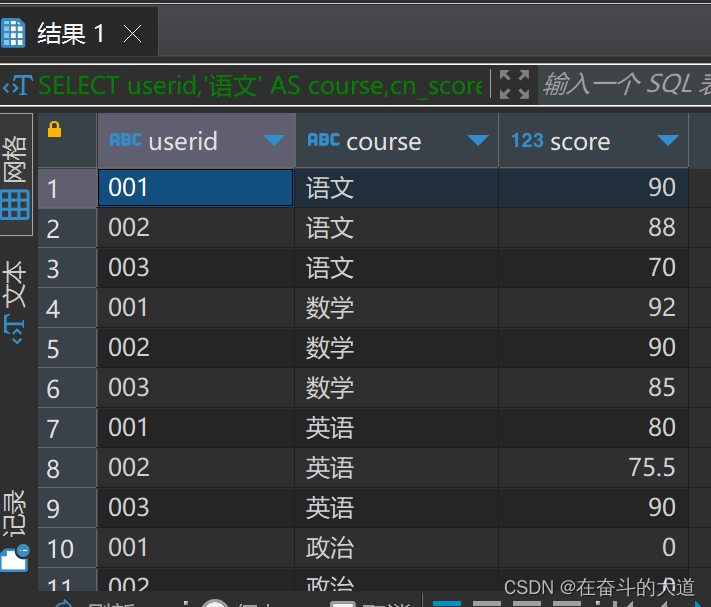
MySQL 搞定行转列,列转行
行转列方法总结1、使用case…when…then2、使用SUM(IF()) 生成列3、使用SUM(IF()) 生成列 WITH ROLLUP 生成汇总行4、使用SUM(IF()) 生成列 UNION 生成汇总行,并利用 IFNULL将汇总行标题显示为 Total5、使用SUM(IF()) 生成列,直接生成汇总结果,不再利用…...
正点原子裸机开发之C语言点灯程序
一. 简介 本文针对 IMX6ULL 的裸机开发的(即不带Linux操作系统的开发)。 主要分两部分的工作: 1. 配置 C语言运行环境 2. C 语言编写及运行 二. 配置C语言运行环境 配置 C 语言运行环境的工作分 三部分。如下: 1. 设置…...

cv::阈值分割OTUS原理+代码
opencv库的阈值分割分为全局分割和局部分割全局分割:普通分割ret1,th1 cv2.threshold(img,127, 255, cv2.THRESH_BINARY) #127为阈值 #cv2.THRESH_BINARY |cv2.THRESH_BINARY_INV | cv2.THRESH_TRUNC|cv2.THRESH_TOZERO|cv2.THRESH_TOZERO_INV局部分割:…...
Postgresql-12.5 visual studio-2022 windows 添加pg工程并调试
pg内核学习,记录一下 文章目录安装包编译安装VS添加Postgresql工程调试源码安装包 (1)perl下载 https://www.perl.org/get.html (2)diff下载 http://gnuwin32.sourceforge.net/packages/diffutils.htm (…...

长沙学院2023 第一次蓝桥训练题解
每道题都在洛谷上,每个题都有很详细的题解,可以先自行做,不会再看题解。 题目解析思路都写在代码中,中文题面就不单独解释题意了。 P2440 木材加工(二分答案) 链接:P2440 木材加工 解析 代码…...

云端Docker搭建ABY库以及本地CLion使用
文章目录ABY的搭建以及使用前言ABY库的下载、安装及测试CLion配置后续杂项项目改名使用其他的库最后ABY的搭建以及使用 前言 仅做记录,仅供参考,不同人有不同的使用方式命令手敲,可能有错,自己辨识勿问,我懂的也不多…...

ES6-箭头函数、解构赋值、对象简写
箭头函数特点 1、 (只有1个形参) 可以省略() 2、 {} 可以省略 只有一句代码 或 只有返回值的时候,省略return 3、arguments 不可用,arguments在没有形参的时候可以拿到调用函数拿在的实参 获取伪数组通过Array.from转为真数组。 4、 箭头函数没有this, …...
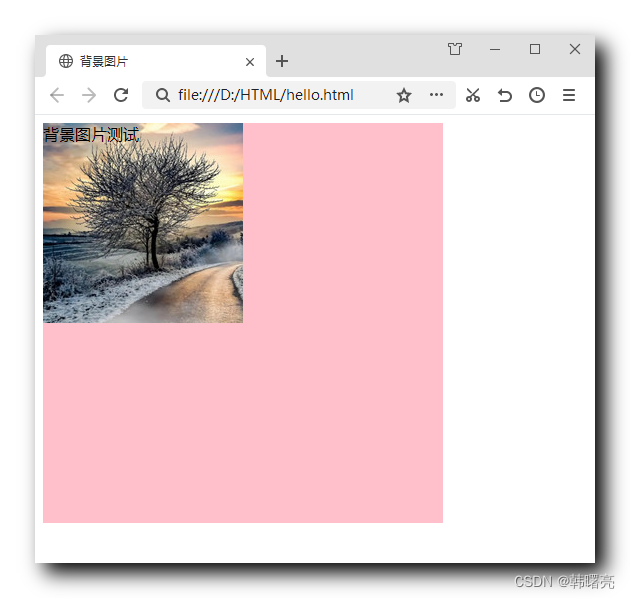
【CSS】CSS 背景设置 ② ( 背景位置 | 背景位置-方位值设置 )
文章目录一、背景位置1、语法说明2、注意事项二、背景位置-方位值设置1、效果展示2、完整代码示例一、背景位置 1、语法说明 如果 盒子的大小 大于 背景图片的大小 , 默认的 图片 位置是 左上角 ; 设置背景位置的 CSS 语法如下 : background-position : length length backgro…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
