【数据结构】第十八弹---C语言实现堆排序

✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】【C++详解】
目录
1、堆排序
1.1、基本思想
1.2、初步代码实现
1.3、代码优化
1.4、代码测试
总结
1、堆排序
在博主数据结构第十二弹---堆的应用有详细讲解堆排序喔~~~
数据结构第十二弹---堆的应用https://blog.csdn.net/2201_75584283/article/details/135348207![]() https://blog.csdn.net/2201_75584283/article/details/135348207
https://blog.csdn.net/2201_75584283/article/details/135348207
1.1、基本思想
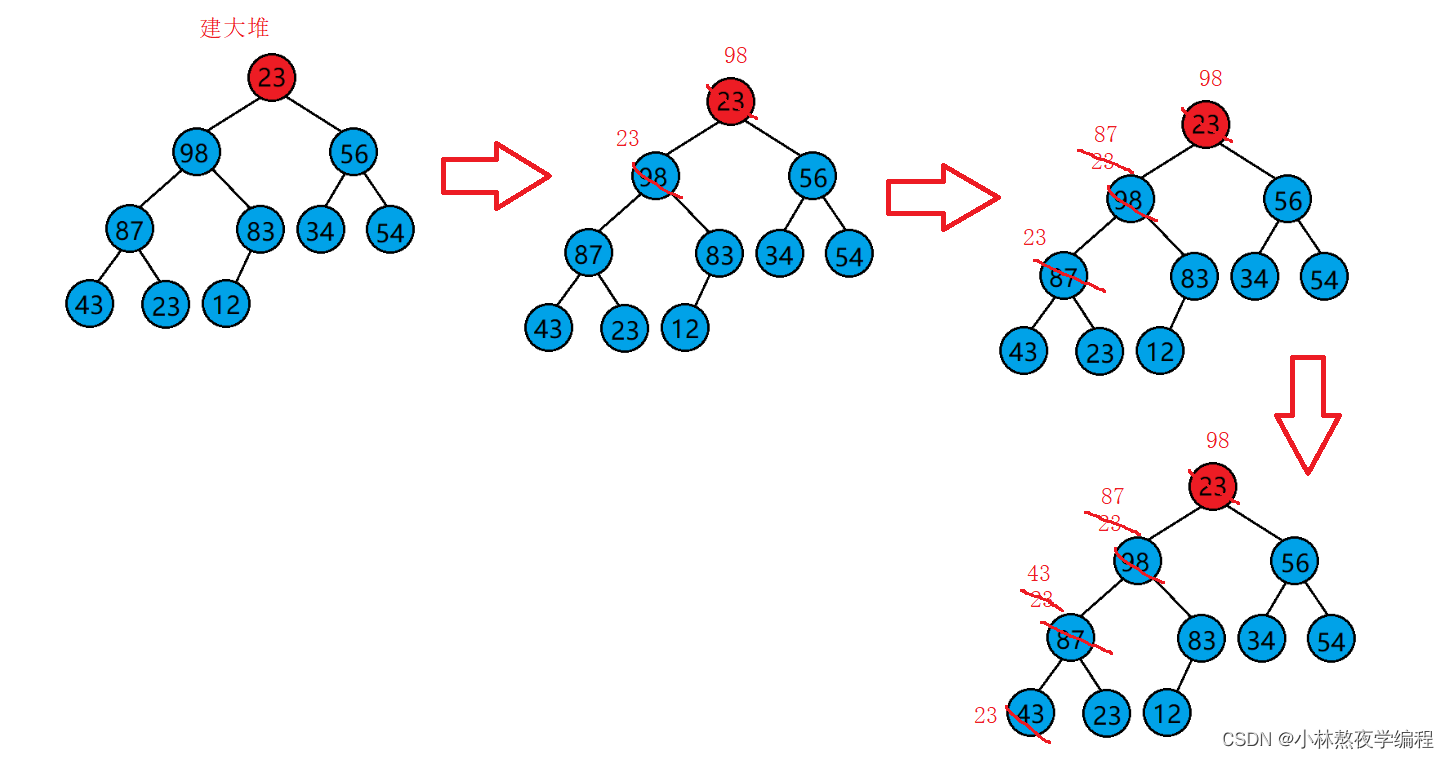
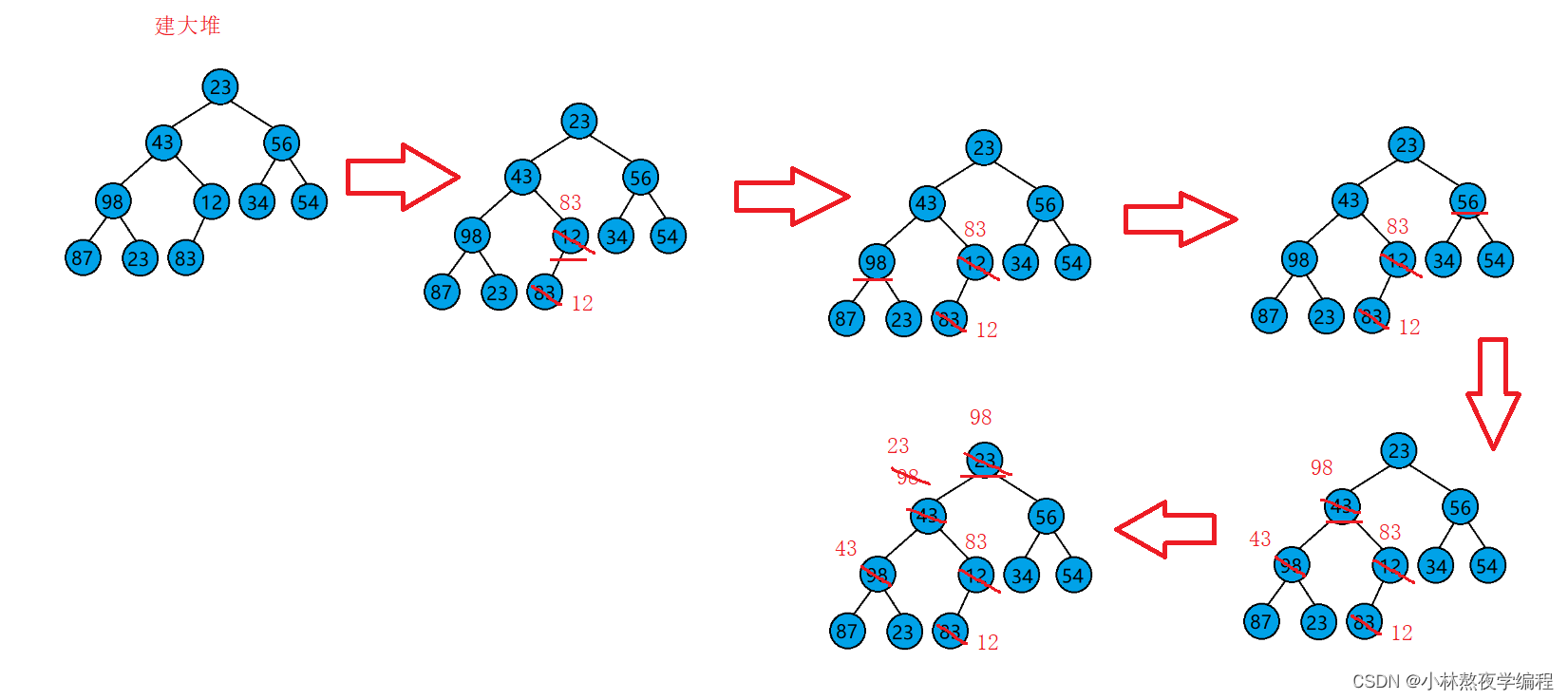
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
为什么升序用到的是大堆呢?
因为:大堆的堆顶是最大的数,可以将其放在数组尾,然后再通过向下调整算法找到次大的数。而小堆的堆顶是最小的数,需要放在第一个位置,如果用原来的堆找不到次小的数,而重新建堆则会更加繁琐。
降序用小堆同理。
动图如下:

1.2、初步代码实现
堆排序的实现可以分为两部分:构建最大堆(或最小堆)和执行排序过程。
注意:此处我们实现的是大堆!!!
第一步:建堆
我们此处是对数组内部的数进行排序,那么怎样才能创建成大堆呢?
这里我们可以使用向上调整算法,从第二个数开始遍历数组,如果不满足大堆则交换父子元素。
for (int i = 1; i < n; i++)
{AjustUp(a, i);
}
大堆向上调整:
- 将被调整的数值与其父节点比较,若是大于父节点,则与父节点交换。
- 若子节点下标为child,父节点下标为(child - 1) / 2。
- 当子节点小于父节点时,或者当子节点已经为堆顶时,停止比较。
代码实现:
void AdjustUp(int* a, int child)
{int parent = 0;while (child > 0){parent = (child - 1) / 2;if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;}else{break;}}
}
小堆向上调整:
与向下调整大堆思想的唯一区别就是:将被调整的数值与父节点比较,若是小于父节点,则与父节点交换,将小根堆比较条件改为小于即可
if (a[child] < a[parent])//孩子小于父亲则交换
{...
}每次向上调整算法的时间复杂度为O(log N)。
所以使用向上调整建好堆的时间复杂度为(N*log N)
第二步:执行排序操作
进行了向上调整之后,此时的数组就是一个大堆了,要怎样才能达到升序呢?
- 使用大根堆选出最大的数,放在数组的最后一个位置,依次选出进行排序。
- 将堆顶和最后一个数交换。
- 然后将新堆顶向下调整,形成堆。
- 向下调整时,注意交换后的最后位置不在新堆里,所以要下标要减一。
- 没有对堆结构造成破坏,不用对每个数都调整。
//2.向下调整 O(N*logN)
int end = n - 1;
while (end > 0) //从最后一个位置开始交换并调整
{Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//此处为大根堆向下调整方式end--;
}大堆向下调整:
- 将被调整的数值与其最大的子节点比较,若是小于最大的子节点,则与该子节点交换。
- 若父节点下标为parent,左子节点下标为 parent * 2 + 1,右子节点的下标为 parent * 2 + 2。
- 获取最大的子节点时,可以先将左子节点作为最大节点,再与右子节点比较,若是大于右子节点,则将左子节点下标加1得到右子节点下标。
- 再循环体内比较左右子节点之前,要先判断右子节点存在,防止堆最后一个节点是左子节点造成越界访问。
- 当子节点小于父节点时,或者当子节点超过堆的范围时,停止比较。
//向下调整算法 大堆
void AdjustDown(int* a, int size, int parent)
{//1.假设左孩子为小的数据int child = parent * 2 + 1;while (child < size){//2.如果左孩子>右孩子 则将右孩子赋值//有可能只有左孩子 所以加条件//以下未有左右孩子且左孩子>右孩子情况,则将child++if (child + 1 < size && a[child] < a[child + 1]){child++;}//3.将孩子与父亲进行比较 如果孩子小则交换//然后将父亲和孩子移动到下一个位置if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}小堆向下调整:
- 将被调整的数值与其最小的子节点比较,若是大于最小的子节点,则与该子节点交换。
- 将小根堆向下调整时左右子节点的比较条件和父节点与子节点的比较改为小于即可。
if (child + 1 < size && a[child] > a[child + 1])
{...
}if (a[child] < a[parent])
{...
}堆排序的代码如下:
void HeapSort(int arr[], int n)
{assert(arr);//1.建堆 向上调整 O(N*logN)for (int i = 1; i < size; i++){AdjustUp(arr, i);}//2.向下调整 O(N*logN)int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}1.3、代码优化
在建堆的时候,我们既可以使用向上调整算法建堆,也可以使用向下调整算法建堆,在堆的应用那一弹我们计算了向下调整算法建堆的时间复杂度,对整个数组进行向下调整的时间复杂度是O(N),因此我们在堆排序的时候也可以统一使用向下调整算法!!!
向下调整:
- 向下调整是从后往前调整,先将后面构成堆,再调整上面的节点。
- 以叶子节点作为根进行向下调整是完全没有必要的,叶子节点没有子节点,所以对最后一个叶子节点的父节点开始向下调整。
- 最后一个节点下标是n-1,它的父节点为 (n-1-1) / 2。
//1.向下调整建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--)//从n-2 到 0 进行调整
{AdjustDown(arr, n, i);
}
堆排序代码如下:
void HeapSort(int arr[], int n)
{assert(arr);//1.向下调整建堆 O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--)//从n-2 到 0 进行调整{AdjustDown(arr, n, i);}//2.向下调整 O(N*logN)int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}1.4、代码测试
测试代码:
//测试堆排序
int main()
{int a[] = { 9,8,7,6,5,4,3,2,1,0 };//给一组数据int sz = sizeof(a) / sizeof(a[0]);//计算数组元素个数printf("排序前:\n");ArrayPrint(a, sz);HeapSort(a, sz);printf("排序后:\n");ArrayPrint(a, sz);return 0;
}测试结果:
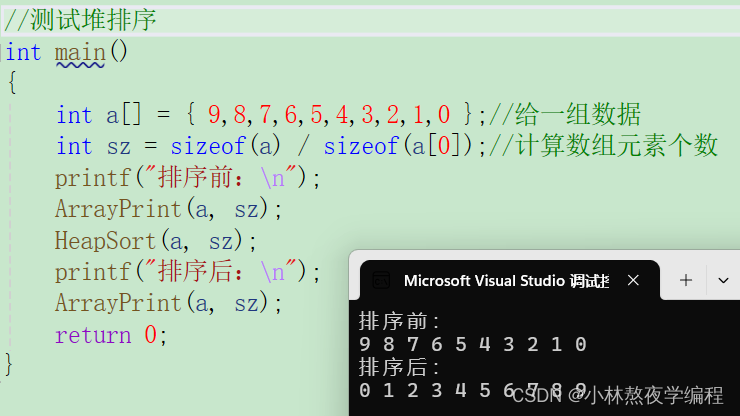
堆排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)。
3. 空间复杂度:O(1)。
4. 稳定性:不稳定。5. 复杂性:复杂。
总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!
相关文章:

【数据结构】第十八弹---C语言实现堆排序
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、堆排序 1.1、基本思想 1.2、初步代码实现 1.3、代码优化 1.4、代码测试 总结 1、堆排序 在博主数据结构第十二弹---堆的应用有详细讲解堆…...

[面试题]Kafka
[面试题]Java【基础】[面试题]Java【虚拟机】[面试题]Java【并发】[面试题]Java【集合】[面试题]MySQL[面试题]Maven[面试题]Spring Boot[面试题]Spring Cloud[面试题]Spring MVC[面试题]Spring[面试题]MyBatis[面试题]Nginx[面试题]缓存[面试题]Redis[面试题]消息队列[面试题]…...
centos7 离线安装zip和unzip
解压的时候发现不能解压,报-bash: unzip: command not found 1、访问https://www.rpmfind.net/linux/rpm2html/search.php?queryzip&submitSearch…&systemcentos&arch#/ 2、输入zip和centos搜索,选择el7下载 3、输入unzip和centos搜索&am…...

Linux下lsof命令使用
目录 lsof 命令使用指南基本语法常用选项使用示例 lsof vs netstatlsofnetstat区别示例对比 lsof 命令使用指南 lsof (List Open Files) 是一个用于列出当前系统中打开文件的命令,适用于 Unix 和类 Unix 操作系统。它不仅可以列出常规文件,还可以列出打…...

基于ChatGPT的大型语言模型试用心得
近年来,ChatGPT这样的大型语言模型,它如同一颗冉冉升起的新星,迅速在商业、教育、娱乐等多个领域照亮了创新的天空,极大地革新了我们的工作与日常生活。 最近我发现一些国内用户也能自由访问的中文ChatGPT APP。这个平台不仅提供…...
)
Python 列表添加多个值(四种方法)
Python 列表添加多个值有多种方法,以下是其中几种实现方法: 一、使用extend()方法 Python 中列表对象有一个 extend() 方法,它可以一次性添加另一个列表中的所有元素到当前列表中。 例1: a = [1, 2, 3] b = [4, 5, 6] a.extend(b)...
VMware RedHat虚拟机磁盘扩容(添加磁盘和扩展磁盘)
前言 自己的电脑上配一个虚拟机还是很有必要的,用起来比双系统方便一点,之前搞了100g的ubuntu没用到,后面重装redhat觉得随便搞个20g就够用了,后面用到之后就遇到磁盘不够用的情况,只能说情况允许的话,磁盘…...

最近,GPT-4o横空出世。对GPT-4o这一人工智能技术进行评价,包括版本间的对比分析、GPT-4o的技术能力以及个人整体感受等
GPT-4o是一款引人瞩目的人工智能技术,它在之前版本的基础上取得了长足的进步。本文将对GPT-4o进行评价,包括版本间的对比分析、GPT-4o的技术能力以及个人整体感受等。 首先,我们来进行GPT-4o与之前版本的对比分析。GPT-4o相较于GPT-3和GPT-2…...

C#面:C#支持多重继承么?
C#不支持多重继承。在C#中,一个类只能直接继承自一个基类。这是由于C#的设计目标之一是避免多重继承可能带来的复杂性和潜在的问题。 然而,C#提供了接口(interface)的概念来实现类似多重继承的功能。一个类可以实现多个接口&…...
细说MCU修改回调函数调用模式的方法
目录 1、硬件及工程 2、实现方法 (1)修改while(1)中的代码: (2)修改2 (3)修改3 (4)修改4 (5)修改5 3、下载并运行 在本文作者的文章中&a…...
Java共享台球室无人系统支持微信小程序+微信公众号
共享台球室无人系统 🎱 创新台球体验 近年来,共享经济如火如荼,从共享单车到共享汽车,无一不改变着我们的生活方式。而如今,这一模式已经渗透到了更多领域,共享台球室便是其中之一。不同于传统的台球室&a…...

如何开发一个海外仓系统?难度在哪,怎么选择高性价解决方案
作为海外仓管理的重要工具,海外仓系统的实际应用价值还是非常高的。为了让大家能更好的理解wms海外仓系统,今天会介绍海外仓系统开发的逻辑架构,以及作为海外仓企业要怎么确定高性价比的数字化管理解决方案。 1、开发海外仓系统要考虑的功能…...

计算机组成原理(Wrong Question)
目录 一、计算机系统概述 *1.1 计算机发展历程 1.2 计算机系统层次结构 1.3 计算机的性能指标 二、 数据的表示和运算 2.1 数制和编码 2.2 运算方法和运算电路 2.3 浮点数的表示与运算 三、存储系统 3.1 存储器概述 3.2 主存储器 3.3 主存储器与CPU的连接 3.4 外部…...

ACL2024 | AI的时空穿越记:大型语言模型共时推理的奇幻之旅!
作者:苏肇辰 标题:Living in the Moment: Can Large Language Models Grasp Co-Temporal Reasoning? 录取:ACL2024 Main 论文链接:https://arxiv.org/abs/2406.09072 代码链接:https://github.com/zhaochen0110/Cotem…...
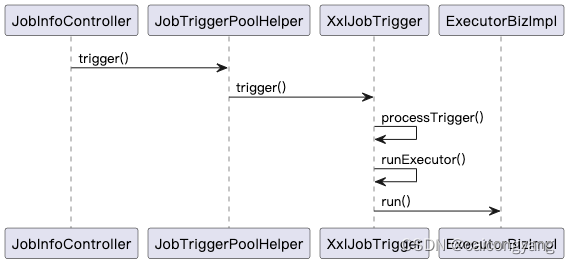
从xxl-job源码中学习Netty的使用
1. 启动与Spring实例化 com.xxl.job.core.executor.impl.XxlJobSpringExecutor.java类 继承SmartInitializingSingleton 类,在afterSingletonsInstantiated 实例化后方法中 调用initJobHandlerMethodRepository 把所有的xxljob任务管理起来; private…...

人工智能发展历程了解和Tensorflow基础开发环境构建
目录 人工智能的三次浪潮 开发环境介绍 Anaconda Anaconda的下载和安装 下载说明 安装指导 模块介绍 使用Anaconda Navigator Home界面介绍 Environment界面介绍 使用Jupter Notebook 打开Jupter Notebook 配置默认目录 新建文件 两种输入模式 Conda 虚拟环境 添…...

makefile追加warning日志
在Makefile中,你不能直接“追加”warning日志到构建过程中,但你可以通过几种方式在构建时产生额外的警告或消息。以下是一些常用的方法: 使用echo或printf命令: 在Makefile的规则中,你可以使用echo或printf命令来输出警…...

不要直接使用unidefined 而使用void 0
为什么不要使用unidefined 而使用void 0? 在JavaScript中,undefined 和 void 0 都可以用来表示未定义的值,但它们在使用和上下文中有一些微妙的差异,这也是为什么有时可能会推荐使用 void 0 而不是直接使用 undefined。 全局污染ÿ…...

注解详解系列 - @Scope:Bean作用域管理
注解简介 在今天的注解详解系列中,我们将探讨Scope注解。Scope是Spring框架中的一个重要注解,用于定义Spring bean的作用域。通过指定bean的作用域,我们可以控制bean的生命周期和创建方式。 注解定义 Scope注解用于指定Spring bean的作用域…...

数学建模基础:数学建模概述
目录 前言 一、数学建模的步骤 二、模型的分类 三、模型评价指标 四、常见的数学建模方法 实际案例:线性回归建模 步骤 1:导入数据 步骤 2:数据预处理 步骤 3:建立线性回归模型 步骤 4:模型验证 步骤 5&…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
