数学建模基础:数学建模概述
目录
前言
一、数学建模的步骤
二、模型的分类
三、模型评价指标
四、常见的数学建模方法
实际案例:线性回归建模
步骤 1:导入数据
步骤 2:数据预处理
步骤 3:建立线性回归模型
步骤 4:模型验证
步骤 5:模型应用
总结
前言
数学建模是将实际问题转化为数学形式进行分析和解答的过程。它是解决复杂科学和工程问题的重要工具。本文将详细介绍数学建模的基本概念、步骤、模型分类及常见的数学建模方法。
一、数学建模的步骤
数学建模通常包含以下几个步骤:
- 问题分析
- 对实际问题进行详细分析,明确其目标和限制条件。通过剖析问题,了解其内在结构和特征。
% 示例:分析一个简单的物流优化问题
- 模型假设
- 根据问题的实际情况,进行合理的简化和假设。这有助于提炼出主要因素,忽略次要因素,使问题变得可操作。
% 示例:假设物流问题中货运车辆的容量和线路固定
- 模型建立
- 在明确目标和假设的基础上,运用数学工具建立数学模型。常用的工具包括代数方程、微分方程、统计模型等。
% 示例:建立一个简单的线性规划模型% 目标函数:minimize cost = f(x)
- 模型求解
- 采用合适的算法或数值方法求解数学模型。Matlab 提供了丰富的求解工具,例如解线性方程组、优化算法等。
% 示例:使用 Matlab 求解线性规划问题% result = linprog(f, A, b)
- 模型验证
- 将模型求解结果与实际数据进行比较,验证模型的合理性和准确性。如有偏差,需修改模型或重新进行假设。
% 示例:利用实际物流数据验证模型的预测结果
下表总结了数学建模的步骤:
| 步骤 | 说明 | 示例 |
|---|---|---|
| 问题分析 | 详细分析实际问题,明确目标和限制条件 | 分析物流优化问题 |
| 模型假设 | 进行合理的简化和假设 | 假设车辆容量和路线固定 |
| 模型建立 | 建立适合的数学模型 | 建立线性规划模型 |
| 模型求解 | 使用适当的算法或数值方法求解模型 | 使用 Matlab 解线性规划问题 |
| 模型验证 | 比较模型结果与实际数据,验证其合理性 | 使用实际数据验证模型 |
二、模型的分类
根据问题的不同和数学工具的使用,数学模型可以分为以下几类:
- 线性模型
- 线性模型通过线性方程描述变量之间的关系,适用于许多工程和科学问题。常见的例子包括线性回归、线性规划等。
% 示例:线性回归x = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 5];p = polyfit(x, y, 1); % 线性回归
- 非线性模型
- 非线性模型用于描述变量之间的非线性关系。对应的数学形式更为复杂,但可以更准确地描述实际问题。常见的例子包括非线性回归、非线性规划等。
% 示例:非线性回归f = @(b, x) b(1) * exp(b(2) * x);beta0 = [1, 1]; % 初始猜测值beta = nlinfit(x, y, f, beta0); % 非线性回归
- 统计模型
- 统计模型通过概率和统计学方法描述数据的分布和关系,广泛应用于数据分析、市场调查等领域。常见的例子包括回归分析、时间序列分析等。
% 示例:时间序列分析ts = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];values = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20];mov_avg = movmean(values, 3); % 移动平均
- 微分方程模型
- 微分方程模型通过微分方程描述系统的动态行为,广泛应用于物理、化学、生物等领域。常见的例子包括常微分方程、偏微分方程等。
% 示例:常微分方程dydt = @(t, y) t * y;[t, y] = ode45(dydt, [0, 2], 1); % 求解微分方程
下表总结了不同类型的数学模型:
| 模型类型 | 说明 | 示例 |
|---|---|---|
| 线性模型 | 通过线性方程描述变量之间的关系 | 线性回归,线性规划 |
| 非线性模型 | 用于描述变量之间的非线性关系 | 非线性回归,非线性规划 |
| 统计模型 | 使用概率和统计方法描述数据分布和关系 | 回归分析,时间序列分析 |
| 微分方程模型 | 通过微分方程描述系统的动态行为 | 常微分方程,偏微分方程 |
三、模型评价指标
在建立和求解数学模型后,需要对模型进行评价,以判断其适用性和准确性。常见的评价指标包括:
- 误差分析
- 通过计算模型预测值与实际值之间的差异来评估模型的准确性。常用的误差指标包括均方误差(MSE)、平均绝对误差(MAE)等。
actual = [1, 2, 3, 4, 5];predicted = [1.1, 1.9, 3.2, 3.8, 5.1];mse = mean((actual - predicted).^2); % 均方误差mae = mean(abs(actual - predicted)); % 平均绝对误差
- 模型验证
- 通过将模型应用于独立的数据集来检验其通用性,即验证集或交叉验证。常用的方法包括留一法交叉验证、k折交叉验证等。
% 示例:k折交叉验证cv = cvpartition(length(actual), 'KFold', 5);for i = 1:cv.NumTestSetstrain_idx = training(cv, i);test_idx = test(cv, i);% 使用训练集训练模型% 使用测试集验证模型end
- 灵敏度分析
- 分析模型对输入参数变化的敏感程度,以确定哪些参数对模型结果影响最大。在参数优化和不确定性分析中尤为重要。
% 示例:简单的灵敏度分析params = linspace(0.9, 1.1, 5); % 假设某一参数在 0.9 到 1.1 之间变化results = arrayfun(@(p) model(p), params); % 模型对不同参数取值的结果
- 稳健性分析
- 检查模型在不同条件下的稳健性,评估模型在面对数据噪声和不确定性时的表现。
% 示例:添加噪声进行稳健性分析noise_levels = linspace(0, 0.1, 5);results = arrayfun(@(n) model(data + n * randn(size(data))), noise_levels);
下表总结了常见的模型评价指标:
| 评价指标 | 说明 | 示例 |
|---|---|---|
| 误差分析 | 评估模型预测值与实际值之间的误差 | 均方误差、平均绝对误差 |
| 模型验证 | 检验模型在独立数据集上的表现 | k折交叉验证 |
| 灵敏度分析 | 分析模型对输入参数变化的敏感性 | 参数变化对模型结果的影响 |
| 稳健性分析 | 评估模型在数据噪声和不确定性下的表现 | 添加噪声进行稳健性评估 |
四、常见的数学建模方法
数学建模中有许多常见的方法和工具,能够帮助我们建立和求解各种数学模型。以下是几种常见的数学建模方法,包括线性规划、非线性规划、回归分析、微分方程等。
- 线性规划
- 线性规划是优化问题的一种,目标是最大化或最小化线性目标函数,约束条件也是线性的。线性规划广泛应用于生产计划、资源分配等领域。
% 示例:线性规划f = [-1; -1]; % 目标函数系数A = [1, 2; 4, 1; -1, -2]; % 约束系数矩阵b = [3; 6; -3]; % 约束值lb = [0; 0]; % 变量下界[x, fval] = linprog(f, A, b, [], [], lb, []); % 求解线性规划问题
- 非线性规划
- 非线性规划用于求解目标函数或约束条件为非线性的问题。常见的求解方法包括梯度下降法、信赖域方法等。
% 示例:非线性规划fun = @(x) x(1)^2 + x(2)^2; % 目标函数x0 = [1, 1]; % 初始值[x, fval] = fminunc(fun, x0); % 求解非线性规划问题
- 回归分析
- 回归分析用于研究自变量与因变量之间的关系,广泛应用于数据分析、预测等领域。常见的回归模型包括线性回归、非线性回归、多元回归等。
% 示例:多元线性回归X = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 自变量y = [1; 2; 3]; % 因变量b = regress(y, X); % 求解回归系数
- 微分方程
- 微分方程用于描述系统的动态行为,广泛应用于物理、化学、生物等领域。常见的微分方程模型包括常微分方程、偏微分方程等。
% 示例:常微分方程dydt = @(t, y) t * y; % 微分方程[t, y] = ode45(dydt, [0, 2], 1); % 求解微分方程
- 蒙特卡罗模拟
- 蒙特卡罗模拟通过随机采样的方法解决复杂系统问题,常用于风险评估、概率分析等领域。
% 示例:蒙特卡罗模拟n = 10000; % 模拟次数results = zeros(n, 1);for i = 1:nx = randn(); % 生成随机数results(i) = exp(x); % 应用模型endmean_result = mean(results); % 计算期望值
下表总结了常见的数学建模方法及其示例:
| 方法 | 说明 | 示例 |
|---|---|---|
| 线性规划 | 最大化或最小化线性目标函数,约束条件也是线性 | linprog 求解线性规划问题 |
| 非线性规划 | 求解目标函数或约束条件为非线性的问题 | fminunc 求解非线性规划问题 |
| 回归分析 | 研究自变量与因变量之间的关系 | regress 求解线性回归 |
| 微分方程 | 描述系统的动态行为 | ode45 求解微分方程 |
| 蒙特卡罗模拟 | 通过随机采样解决复杂系统问题 | 随机数生成和期望值计算 |
实际案例:线性回归建模
为更好地理解这些数学建模方法,我们通过一个实际的线性回归案例来展示完整的建模过程。
假设我们有一组数据,表示房屋面积与房屋价格的关系。我们的任务是建立一个模型来预测房屋价格。
步骤 1:导入数据
我们的数据存储在一个CSV文件 house_prices.csv,内容如下:
Area,Price
1000,300000
1200,350000
1500,400000
1800,450000
2000,500000
% 导入数据到表格
data = readtable('house_prices.csv');
area = data.Area;
price = data.Price;
步骤 2:数据预处理
在进行回归分析之前,我们可以先对数据进行简单的可视化,检查数据的分布和趋势。
% 绘制散点图
figure;
scatter(area, price, 'filled');
title('House Prices');
xlabel('Area (sq ft)');
ylabel('Price ($)');
grid on;
步骤 3:建立线性回归模型
我们使用 Matlab 内置的 fitlm 函数来建立线性回归模型。
% 建立线性回归模型
model = fitlm(area, price);% 显示模型参数
disp(model);
步骤 4:模型验证
我们可以通过绘制回归线和残差图来验证模型的效果,并计算相关的统计指标来判断模型的准确性。
% 绘制回归线
figure;
plot(area, price, 'o'); % 原始数据点
hold on;
plot(model);
title('Linear Regression');
xlabel('Area (sq ft)');
ylabel('Price ($)');
legend('Data', 'Fit', 'Location', 'Best');
grid on;% 绘制残差图
figure;
plotResiduals(model, 'fitted');
title('Residuals');
grid on;
步骤 5:模型应用
通过训练好的模型,我们可以预测新的房屋面积对应的价格。
% 预测新的房屋价格
new_area = 1600;
predicted_price = predict(model, new_area);
disp(['Predicted price for ' num2str(new_area) ' sq ft: $' num2str(predicted_price)]);
下表总结了建模过程的各个步骤及相应的 Matlab 操作:
| 步骤 | 说明 | 示例 |
|---|---|---|
| 导入数据 | 从CSV文件中导入数据 | readtable('house_prices.csv'); |
| 数据预处理 | 可视化数据,检查分布和趋势 | scatter(area, price, 'filled'); |
| 建立模型 | 使用线性回归建立预测模型 | fitlm(area, price); |
| 模型验证 | 通过绘制回归线和残差图,计算统计指标 | plot(area, price, 'o'); plot(model); |
| 模型应用 | 使用训练好的模型进行预测 | predict(model, new_area); |
总结
本文详细介绍了数学建模的基础知识,包括数学建模的步骤、模型分类、模型评价指标和常见的数学建模方法。在每个部分都提供了相应的 Matlab 示例和表格总结,帮助读者更好地理解和掌握这些知识。通过实际案例的展示,我们了解了如何从数据导入到模型建立、验证和应用的完整过程。掌握这些技能将大大提升我们在科学研究和工程实践中的数据分析和建模能力。
相关文章:

数学建模基础:数学建模概述
目录 前言 一、数学建模的步骤 二、模型的分类 三、模型评价指标 四、常见的数学建模方法 实际案例:线性回归建模 步骤 1:导入数据 步骤 2:数据预处理 步骤 3:建立线性回归模型 步骤 4:模型验证 步骤 5&…...
人工智能大模型之开源大语言模型汇总(国内外开源项目模型汇总)
开源大语言模型完整列表 Large Language Model (LLM) 即大规模语言模型,是一种基于深度学习的自然语言处理模型,它能够学习到自然语言的语法和语义,从而可以生成人类可读的文本。 所谓"语言模型",就是只用来处理语言文…...

数据结构之B树
引言 在计算机科学中,数据结构是用于组织和存储数据的关键工具。其中,B树(B-tree)作为一种自平衡的树形数据结构,被广泛应用于数据库和文件系统中,以提高查找、插入、删除和范围查询的效率。本文将深入探讨…...
,——森林机器学习、时间序列)
双色球预测算法(Java),——森林机器学习、时间序列
最近AI很火,老想着利用AI的什么算法,干点什么有意义的事情。其中之一便想到了双色球,然后让AI给我预测,结果基本都是简单使用随机算法列出了几个数字。 额,,,,咋说呢,双…...
【计算机网络篇】数据链路层(11)在数据链路层扩展以太网
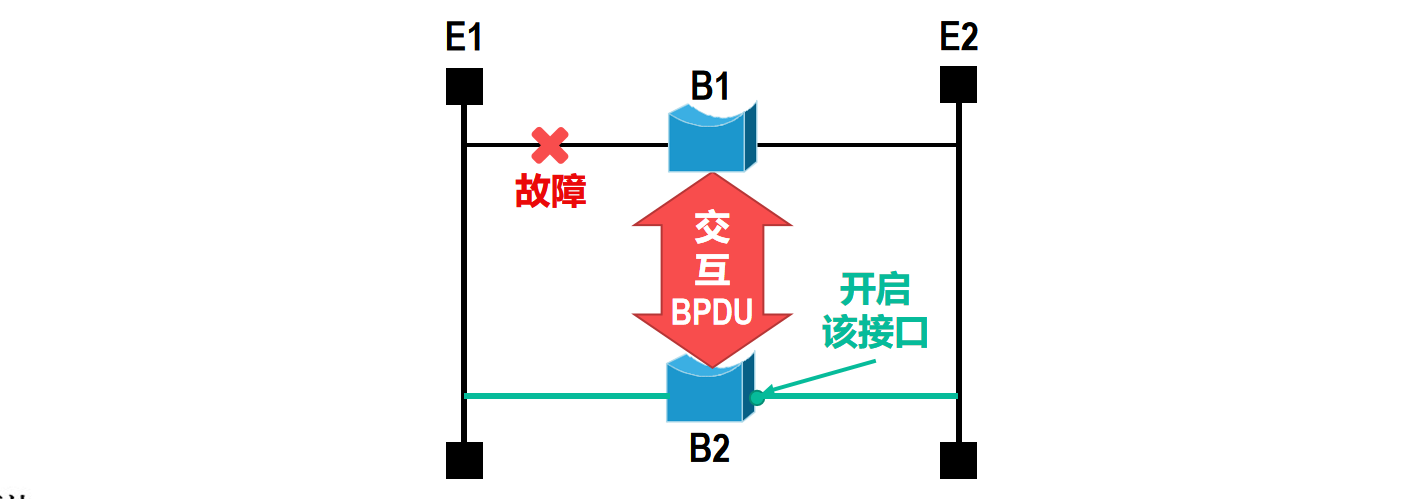
文章目录 🍔使用网桥在数据链路层扩展以太网🥚网桥的主要结构和基本工作原理🎈网桥的主要结构🔎网桥转发帧的例子🔎网桥丢弃帧的例子🔎网桥转发广播帧的例子 🥚透明网桥🔎透明网桥的…...

Ubuntu20.04 使用scrapy-splash爬取动态网页
我们要先安装splash服务,使用dock安装,如果dock没有安装,请参考我的上一篇博文: 按照官方文档:https://splash.readthedocs.io/en/stable/install.html 1.下载splash sudo docker pull scrapinghub/splash2.安装scrapy…...

Function:控制继电器上下电,上电后adb登录,copy配置文件
import serial import time import datetime import subprocess import osdef append_to_txt(file_path, content):if os.path.exists(file_path):with open(file_path, a) as file: # 使用 a 模式打开文件进行追加file.write(content \n) # 追加内容,并换行else…...

香港电讯高可用网络助力企业变革金融计算
客户背景 客户是一家金融行业知名的量化私募对冲基金公司,专注于股票、期权、期货、债券等主要投资市场,在量化私募管理深耕多年,目前资管规模已达数百亿级,在国内多个城市均设有办公地点。 客户需求 由于客户业务倚重量化技术…...
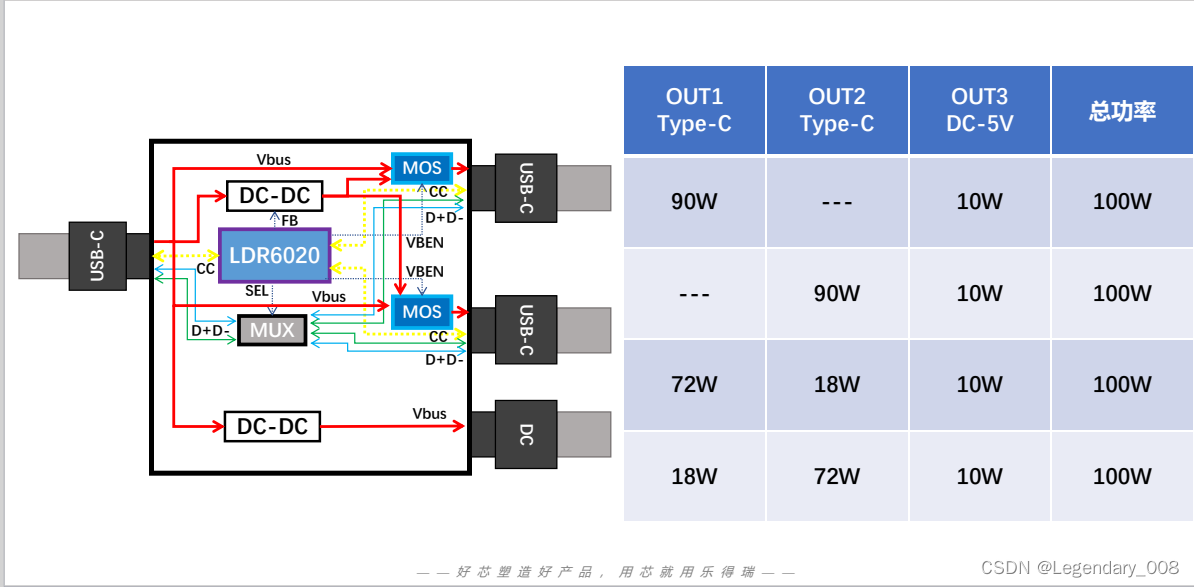
LDR6020一拖二快充线:多设备充电新选择
随着科技的快速发展,我们的日常生活中越来越多地依赖于智能设备。然而,每当手机、平板或其他移动设备电量告急时,我们总是需要寻找合适的充电线进行充电。为了解决这一痛点,市场上出现了一款备受瞩目的新产品——LDR6020一拖二快充…...

电脑ffmpeg.dll丢失原因解析,找不到ffmpeg.dll的5种解决方法
在数字化时代,多媒体文件的处理已经成为我们日常生活和工作中不可或缺的一部分。在计算机使用过程中,丢失ffmpeg.dll文件是一个特定但常见的问题,尤其是对于那些经常处理视频编解码任务的用户来说。下面小编讲全面分析ffmpeg.dll丢失原因以及…...
手机网站制作软件是哪些
手机网站制作软件是一种用于设计、开发和创建适用于移动设备的网站的软件工具。随着移动互联网时代的到来,越来越多的用户开始使用手机浏览网页和进行在线交流,因此,手机网站制作软件也逐渐成为了市场上的热门工具。 1. Adobe Dreamweaver&am…...
【Kubernetes项目部署】k8s集群+高可用、负载均衡+防火墙
项目架构图 (1)部署 kubernetes 集群 详见:http://t.csdnimg.cn/RLveS (2) 在 Kubernetes 环境中,通过yaml文件的方式,创建2个Nginx Pod分别放置在两个不同的节点上; Pod使用hostP…...

IPC工业电脑的现状、发展未来与破局策略
文章目录 全球工业电脑市场概况1.1 市场规模与增长1.2 区域分布与主要市场 工业电脑的技术发展与应用2.1 技术趋势与创新2.2 应用领域扩展2.3 工业自动化与智能化 竞争格局与市场参与者3.1 主要企业与市场竞争3.2 国内外竞争对比3.3 市场集中度与竞争策略 未来发展趋势与市场预…...
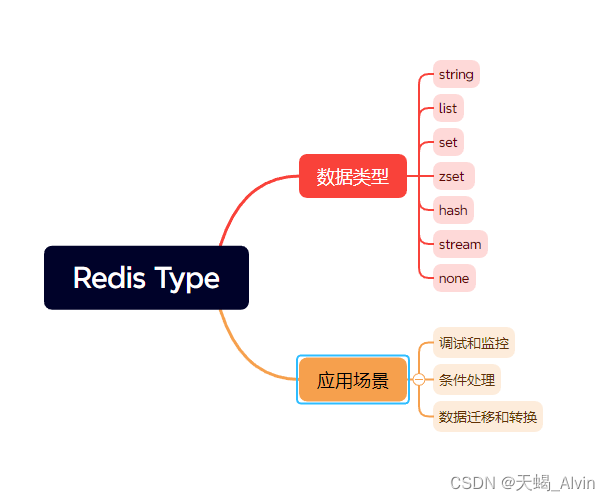
深入了解Redis的TYPE命令
Redis作为一个高性能的内存数据库,支持多种数据结构。在管理和操作Redis数据库时,了解键对应的数据类型是至关重要的。本文将深入探讨Redis的TYPE命令,它用于返回存储在指定键中的值的数据类型。 什么是TYPE命令? TYPE命令用于查…...
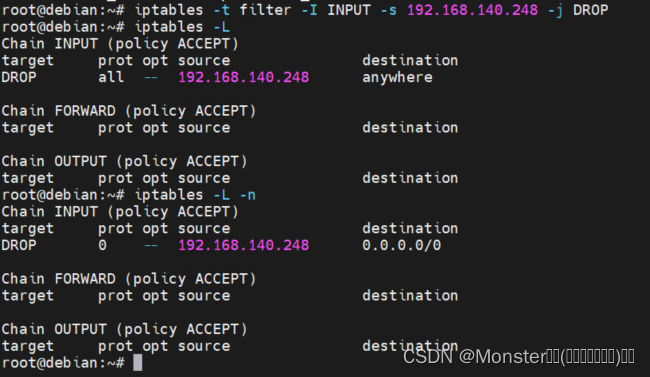
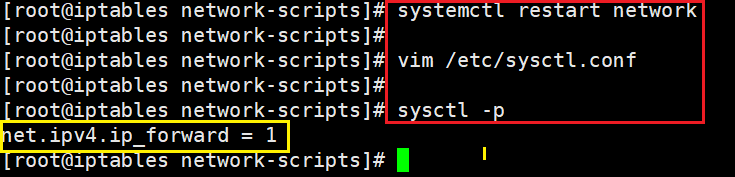
iptables(3)规则管理
简介 上一篇文章中,我们已经介绍了怎样使用iptables命令查看规则,那么这篇文章我们就来介绍一下,怎样管理规则,即对iptables进行”增、删、改”操作。 注意:在进行iptables实验时,请务必在个人的测试机上进行,不要再有任何业务的机器上进行测试。 在进行测试前,为保障…...

关于addEventListener的使用和注意项
一、addEventListener基本理解 addEventListener 是一个 JavaScript DOM 方法,用于向指定元素添加事件监听器。它接受三个参数: 事件类型:一个字符串,表示要监听的事件类型,如 ‘click’、‘mouseover’、‘keydown’…...
分享一下,如何搭建个人网站的步骤
在这段充满探索与创造的奇妙旅途中,我就像一位耐心的建筑师,在数字世界的荒原上精心雕琢,两周的时光缓缓流淌。每天,我与代码共舞,手执HTML、CSS与JavaScript这三大构建魔杖,一砖一瓦地筑起了梦想中的网络城…...

(7)摄像机和云台
文章目录 前言 1 云台 2 带有MAVLink接口的摄像机 3 相机控制和地理标签 4 视频质量差的常见修复方法 5 详细主题 前言 Copter、Plane 和 Rover 最多支持 3 轴云台,包括自动瞄准感兴趣区域(ROI)的相机和自动触发相机快门等先进功能。按…...

MicroBlaze IP核中的外设接口和缓冲器接口介绍
MicroBlaze IP核是Xilinx公司提供的一个嵌入式软核处理器,广泛应用于FPGA设计中。在MicroBlaze IP核中,外设接口和缓冲器接口是处理器与外部设备和内存交互的关键部分。 1 外设接口 MicroBlaze处理器中的AXI4 内存映射外设接口AXI4是一种在Xilinx FPGA设…...
)
Java数据结构与算法(完全背包)
前言: 完全背包问题是背包问题的一个变种,与0/1背包问题不同,在完全背包问题中,每种物品可以被选取多次。问题描述如下: 给定 n 件物品,每件物品有一个重量 wi和一个价值 vi,以及一个背包,它能…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
