代码随想录算法训练营第四十四天 | 322. 零钱兑换、279.完全平方数、139.单词拆分、多重背包理论基础、背包问题总结
322. 零钱兑换
题目链接:https://leetcode.cn/problems/coin-change/
文档讲解:https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html
视频讲解:https://www.bilibili.com/video/BV14K411R7yv/
思路
- 确定dp数组以及下标的含义:凑成金额j最少需要
dp[j]个硬币。 - 确定递推公式:
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);。需要注意的是只有dp[j - coins[i]]不为初始值时才进行计算,不然没有意义。 - dp数组如何初始化:因为求的是最小值,所以初始化为
Integer.MAX_VALUE,dp[0] = 0;,凑成0元需要0个硬币。 - 确定遍历顺序:因为是求最小值且硬币个数无限,所以正序遍历背包和物品,谁先遍历都可以。
- 打印dp数组,用于debug
代码
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];for (int i = 0; i <= amount; i++) dp[i] = Integer.MAX_VALUE;dp[0] = 0;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != Integer.MAX_VALUE) dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}
}
分析:时间复杂度:O(mn),空间复杂度:O(m)。m是amount的值,n是coins的长度。
279.完全平方数
题目链接:https://leetcode.cn/problems/perfect-squares/
文档讲解:https://programmercarl.com/0279.%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0.html
视频讲解:https://www.bilibili.com/video/BV12P411T7Br/
思路
- 确定dp数组以及下标的含义:和为j的完全平方数最小个数为
dp[j]。 - 确定递推公式:
dp[j] = Math.min(dp[j], dp[j - nums[i]] + 1); - dp数组如何初始化:因为是求最小值,所以初始化为最大值,和为0的完全平方数个数为0。
for (int i = 1; i <= n; i++) dp[i] = Integer.MAX_VALUE;
dp[0] = 0;
- 确定遍历顺序:因为是求最小值且硬币个数无限,所以正序遍历背包和物品,谁先遍历都可以。
- 打印dp数组,用于debug
代码
我的代码
class Solution {public int numSquares(int n) {int[] nums = new int[n];int numslen = 0;// 先得到小于n的完全平方数都有哪些,存入数组,作为物品。for (int i = 1; i * i <= n; i++) {nums[numslen++] = i * i;}int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) dp[i] = Integer.MAX_VALUE;dp[0] = 0;for (int i = 0; i < numslen; i++) {for (int j = nums[i]; j <= n; j++) {dp[j] = Math.min(dp[j], dp[j - nums[i]] + 1);}}return dp[n];}
}
卡哥代码
class Solution {public int numSquares(int n) {int[] dp = new int[n + 1];for (int j = 0; j <= n; j++) {dp[j] = Integer.MAX_VALU;}dp[0] = 0;for (int i = 1; i * i <= n; i++) {for (int j = i * i; j <= n; j++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}
分析:时间复杂度:O(n * √n),空间复杂度:O(n)。
139.单词拆分
题目链接:https://leetcode.cn/problems/word-break/
文档讲解:https://programmercarl.com/0139.%E5%8D%95%E8%AF%8D%E6%8B%86%E5%88%86.html
视频讲解:https://www.bilibili.com/video/BV1pd4y147Rh/
思路
- 确定dp数组以及下标的含义:字符串长度为j的话,dp[j]为true,表示可以拆分为一个或多个在字典中出现的单词。
- 确定递推公式:如果确定dp[i] 是true,且 [i, j] 这个区间的子串出现在字典里,那么dp[j]一定是true。所以递推公式是
if (hash.contains(s.substring(i, j)) && dp[i]) dp[j] = true;。 - dp数组如何初始化:
Arrays.fill(dp, false);,dp[0] = true; - 确定遍历顺序:本题其实我们求的是排列数,为什么呢。 拿
s = "applepenapple",wordDict = ["apple", "pen"]举例。
apple,pen是物品,那么我们要求物品的组合一定是apple+pen+apple才能组成applepenapple。
apple+apple`` +pen或者pen+apple+apple` 是不可以的,那么我们就是强调物品之间顺序。
所以说,本题一定是先遍历背包,再遍历物品。 - 打印dp数组,用于debug
代码
class Solution {public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> hash = new HashSet<>(wordDict); // 转换成hash表,能快速判断是否单词存在在字典里boolean[] dp = new boolean[s.length() + 1];Arrays.fill(dp, false);dp[0] = true;for (int j = 1; j <= s.length(); j++) { // 遍历背包for (int i = 0; i < j && !dp[j]; i++) { // 遍历物品if (hash.contains(s.substring(i, j)) && dp[i]) dp[j] = true;}}return dp[s.length()];}
}
分析:时间复杂度:O(n3),空间复杂度:O(n)。因为substr返回子串的副本是O(n)的复杂度(这里的n是substring的长度)。
多重背包理论基础
题目链接:https://kamacoder.com/problempage.php?pid=1066
文档讲解:https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F…
思路
将多重背包中多个物品的数量展开,然后看做是01背包来解决。
代码
import java.util.Scanner;public class Main{public static void main(String [] args) {Scanner sc = new Scanner(System.in);int bagWeight = sc.nextInt();int n = sc.nextInt();int[] weight = new int[n];int[] value = new int[n];int[] nums = new int[n];for (int i = 0; i < n; i++) weight[i] = sc.nextInt();for (int i = 0; i < n; i++) value[i] = sc.nextInt();for (int i = 0; i < n; i++) nums[i] = sc.nextInt();int[] dp = new int[bagWeight + 1];//先遍历物品再遍历背包,作为01背包处理for (int i = 0; i < n; i++) {for (int j = bagWeight; j >= weight[i]; j--) {//遍历每种物品的个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) {dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}System.out.println(dp[bagWeight]);}
}
分析:时间复杂度:O(mnk),空间复杂度:O(n)。m:物品种类个数,n背包容量,k单类物品数量。
背包问题总结
文档讲解:https://programmercarl.com/%E8%83%8C%E5%8C%85%E6%80%BB%E7%BB%93%E7%AF%87.html
相关文章:

代码随想录算法训练营第四十四天 | 322. 零钱兑换、279.完全平方数、139.单词拆分、多重背包理论基础、背包问题总结
322. 零钱兑换 题目链接:https://leetcode.cn/problems/coin-change/ 文档讲解:https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html 视频讲解:https://www.bilibili.com/video/BV14K411R7yv/ 思路 确定dp数组以及下…...
开源AGV调度系统OpenTCS中的路由器(router)详解
OpenTCS中的任务分派器router详解 1. 引言2. 路由器(router)2.1 代价计算函数(Cost functions)2.2 2.1 Routing groups2.1 默认的停车位置选择2.2 可选停车位置属性2.3 默认的充电位置选择2.4 即时运输订单分配 3. 默认任务分派器的配置项4. 参考资料与源…...

关于下载 IDEA、WebStorm 的一些心得感想
背景 实习第一天的时候,睿哥便吩咐我下载一些软件,这些软件以后在写项目的时候会用到,他叫我先装IDEA,WebStorm,微信开发者工具,git,还有Navicat。 这些软件能够被我们正常使用,无非就通过三步…...
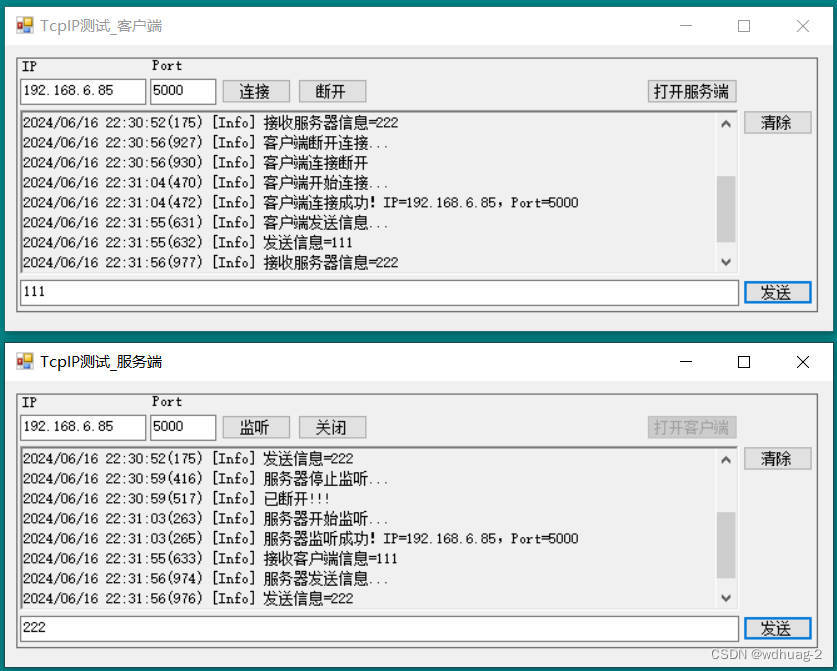
C#使用Scoket实现服务器和客户端互发信息
20240616 By wdhuag 目录 前言: 参考: 一、服务器端: 1、服务器端口绑定: 2、服务器关闭: 二、客户端: 1、客户端连接: 2、客户端断开: 三、通讯: 1、接收信…...

【经验分享】SpringCloud + MyBatis Plus 配置 MySQL,TDengine 双数据源
概述 因为项目中采集工厂中的设备码点的数据量比较大,需要集成TDengine时序数据库,所以需要设置双数据源 操作步骤 导入依赖 <!-- 多数据源支持 --><dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-s…...

Pycharm 忽略文件
安装 .ignore插件 规则示例 罗列一些常遇到.getignore忽略规则的使用示例: 1. 在已忽略文件夹中不忽略指定文件夹: /libs/* !/libs/extend/ 2. 在已忽略文件夹中不忽略指定文件 /libs/* !/libs/extend/fastjson.jar 3.只忽略libs目录…...
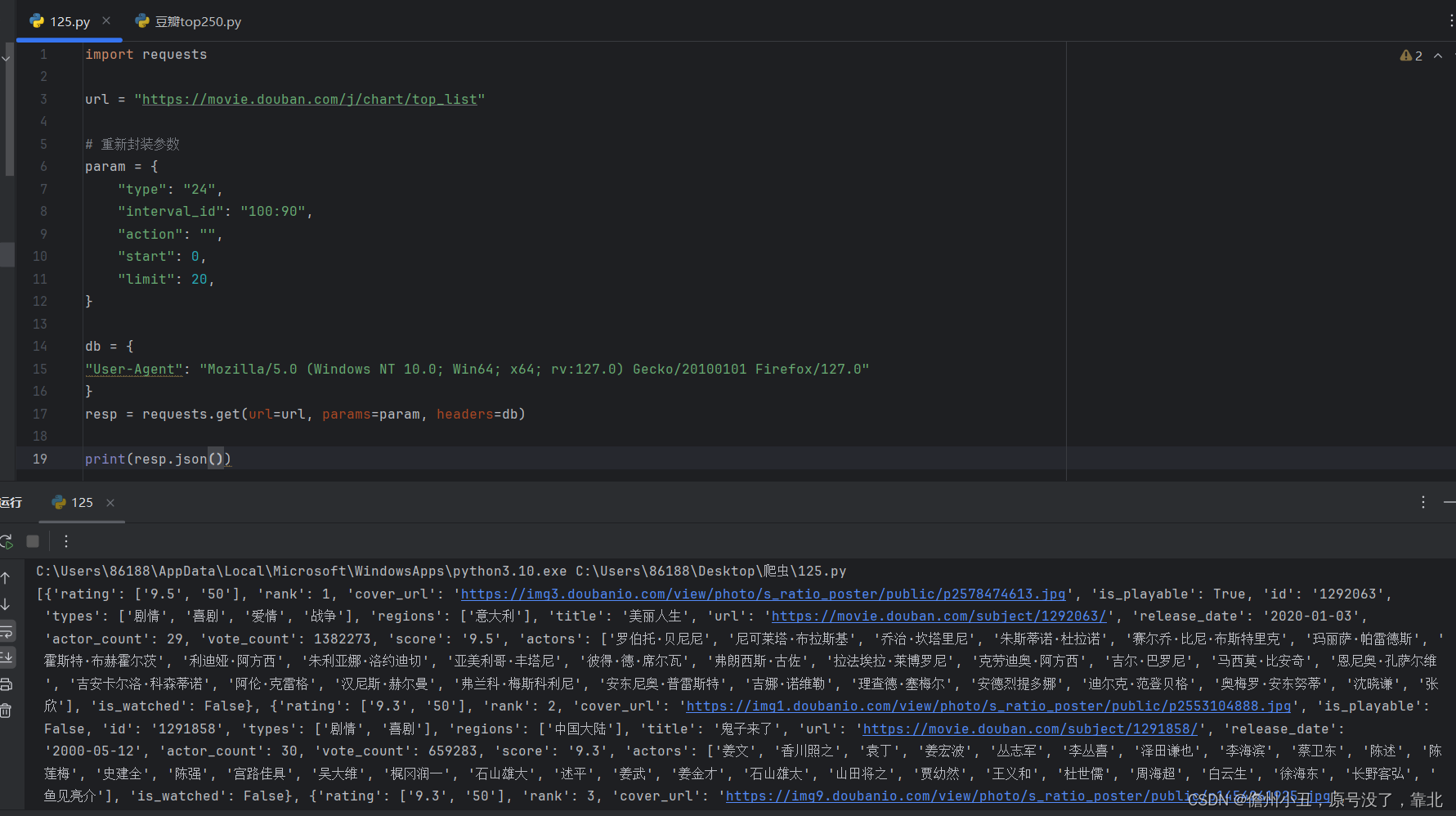
爬虫学习。。。。
爬虫的概念: 爬虫是一种自动化信息采集程序或脚本,用于从互联网上抓取信息。 它通过模拟浏览器请求站点的行为,获取资源后分析并提取有用数据,这些数据可以是HTML代码、JSON数据或二进制数据(如图片、视频)…...

美国铁路客运巨头Amtrak泄漏旅客数据,数据销毁 硬盘销毁 文件销毁
旅客的Guest Rewards常旅客积分账户的个人信息被大量窃取。 美国国家客运铁路公司(Amtrak)近日披露了一起数据泄露事件,旅客的Guest Rewards常旅客积分账户的个人信息被大量窃取。 根据Amtrak向马萨诸塞州提交的泄露通知,5月15日…...
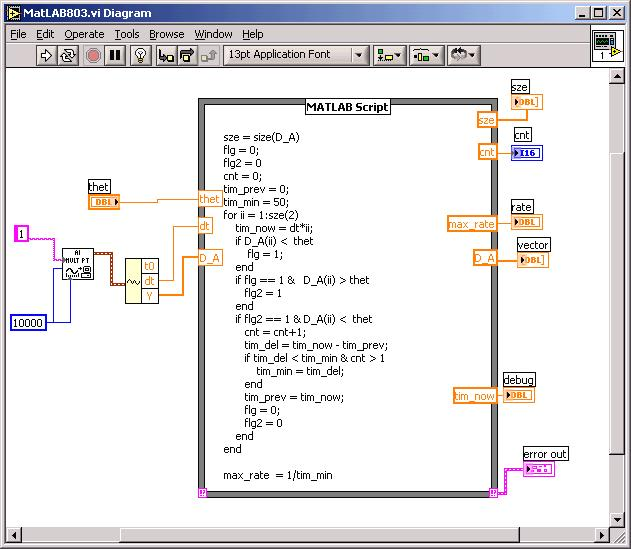
LabVIEW与Matlab联合编程的途径及比较
LabVIEW和Matlab联合编程可以通过多种途径实现,包括调用Matlab脚本节点、使用LabVIEW MathScript RT模块、利用ActiveX和COM接口,以及通过文件读写实现数据交换。每种方法都有其独特的优势和适用场景。本文将详细比较这些方法,帮助开发者…...
秋招突击——6/16——复习{(单调队列优化DP)——最大子序和,背包模型——宠物小精灵收服问题}——新作{二叉树的后序遍历}
文章目录 引言复习(单调队列优化DP)——最大子序和单调队列的基本实现思路——求可移动窗口中的最值总结 背包模型——宠物小精灵收服问题思路分析参考思路分析 新作二叉树的后续遍历加指针调换 总结 引言 复习 (单调队列优化DP)…...
SAR动目标检测系列:【4】动目标二维速度估计
在三大类杂波抑制技术(ATI、DPCA和STAP)中,STAP技术利用杂波与动目标在二维空时谱的差异,以信噪比最优为准则,对地杂波抑制的同时有效保留动目标后向散射能量,有效提高运动目标的检测概率和动目标信号输出信杂比,提供理…...
JavaEE多线程(2)
文章目录 1..多线程的安全1.1出现多线程不安全的原因1.2解决多线程不安全的⽅法1.3三种典型死锁场景1.4如何避免死锁问题2.线程等待通知机制2.1等待通知的作用2.2等待通知的方法——wait2.3唤醒wait的方法——notify 1…多线程的安全 1.1出现多线程不安全的原因 线程在系统中…...

中新赛克两款数据安全产品成功获得“可信数安”评估测试证书
6月19日,2024数据智能大会在北京盛大召开。 会上,中国2024年上半年度“可信数安”评估测试证书正式颁发。中新赛克两款参评产品凭借过硬的技术水准和卓越的应用效果,成功获得专项测试证书。 2024年上半年度“可信数安”评估测试通过名单 中新…...

代码随想录——分割回文串(Leetcode 131)
题目链接 回溯 class Solution {List<List<String>> res new ArrayList<List<String>>();List<String> list new ArrayList<String>();public List<List<String>> partition(String s) {backtracking(s, 0);return res;}p…...

Rust 学习方法及学习路线汇总
Rust 学习方法及学习路线汇总 Rust 是一种系统编程语言,旨在提供安全性、并发性和高性能。它是由 Mozilla 公司开发的,于 2010 年首次发布。Rust 能够帮助开发者编写可靠和高效的软件,因此受到了广泛的关注和认可。 如果你有兴趣学习 Rust&…...

一名女DBA的感谢信,到底发生了什么?
昨日我们收到这样一通来电 “早上九点刚上班便收到业务投诉电话,系统卡顿,接口失败率大增,怀疑数据库问题。打开运维平台发现是国产库,生无可恋,第一次生产环境遇到国产库性能问题,没什么排查经验…...
群晖NAS本地部署并运行一个基于大语言模型Llama2的个人本地聊天机器人
前言 本文主要分享如何在群晖 NAS 本地部署并运行一个基于大语言模型 Llama 2 的个人本地聊天机器人并结合内网穿透工具发布到公网远程访问。本地部署对设备配置要求高一些,如果想要拥有比较好的体验,可以使用高配置的服务器设备. 目前大部分大语言模型的产品都是基于网络线上…...
HarmonyOS模拟器(phone-x86-api9)一直卡顿的解决方法
在DevEco Studio 3.1.1 Release版本中的Device Manager中创建本地的模拟器,创建phone-x86-api9模拟器成功,但是启动该新建的模拟器一直显示"HarmonyOS"logo图片,然后一直卡在这里,运行结果如下所示: 检查模…...

排序题目:有序数组的平方
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:有序数组的平方 出处:977. 有序数组的平方 难度 2 级 题目描述 要求 给定按非递减顺序排序的整…...

PPT可以转换成Word吗?归纳了三种转换方式
PPT可以转换成Word吗?在当今快节奏的工作和学习环境中,不同格式文件之间的转换变得日益重要。PPT作为演示文稿制作的首选工具,广泛应用于会议演讲、教育培训等多个场景,而Word则是文档编辑与编排的基石。为了便于进一步编辑、分享…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
