当前位置： 首页 > news >正文

Mathtype与word字号对照+Mathtype与word字号对照

news 2026/2/9 6:33:51

字体大小对照表如下

初号44pt
小初36pt
一号26pt
小一24pt
二号22pt
小二18pt
三号16pt
小三15pt
四号14pt
小四12pt
五号10.5pt
小五9pt
六号7.5pt
小六6.5pt
七号5.5pt
八号5pt

1 保存12pt文件

首选选择第一个公式，将其大小改为12pt
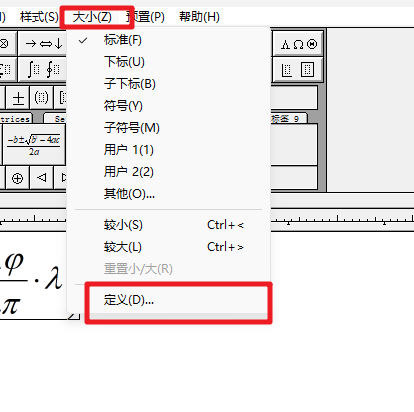
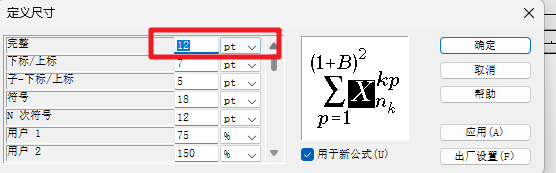
在这里插入图片描述
在这里插入图片描述
然后依次选择 “预置”——> “公式预置”——> “保存到文件”，将这个公式的字体以文件形式保存到桌面（也可以保存到其他文件夹下面，只要自己能找到就行）。

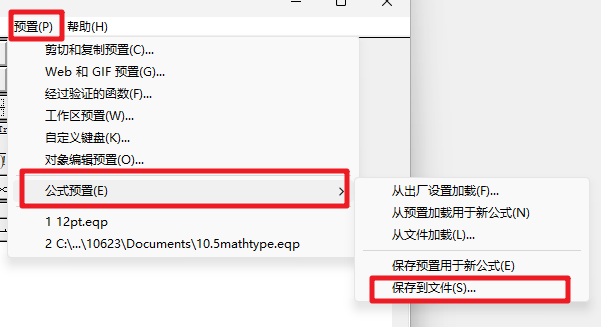
在这里插入图片描述
如下图所示，从保存下来的文件来看，这个文件是.eqp格式 。下面就要用这个12pt.eqp文件将其他公式批量修改即可。
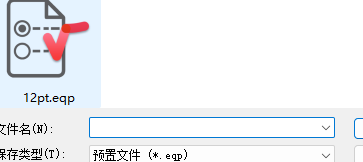
在这里插入图片描述

2 批量修改

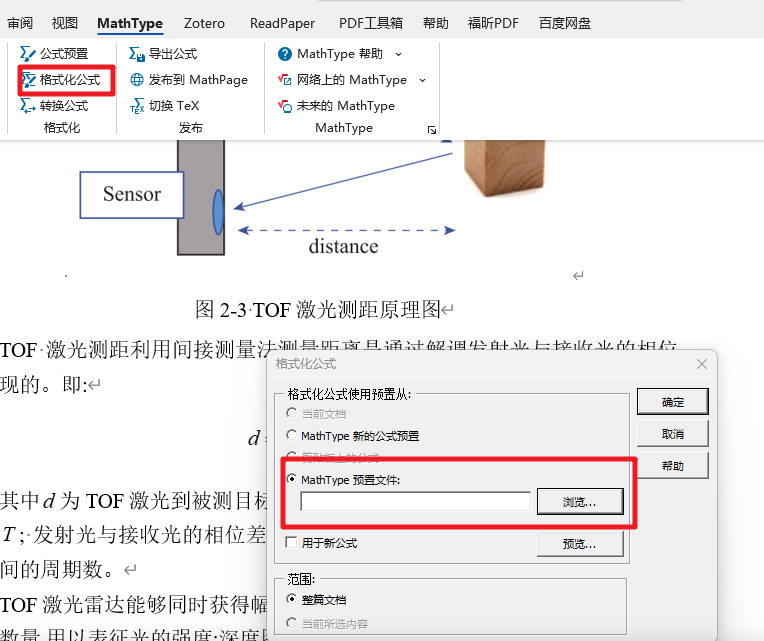
如下图所示。依次选择 “MathType” ——> “格式化公式” ——> “MathType预置文件”——>选择保存在桌面的12pt.eqp文件 ——>“确定”
在这里插入图片描述

相关文章：

Mathtype与word字号对照+Mathtype与word字号对照

字体大小对照表如下 初号44pt 小初36pt 一号26pt 小一24pt 二号22pt 小二18pt 三号16pt 小三15pt 四号14pt 小四12pt 五号10.5pt 小五9pt 六号7.5pt 小六6.5pt 七号5.5pt 八号5pt 1 保存12pt文件 首选选择第一个公式，将其大小改为12pt 然后依次选择 “预置”—…...

编程日记 2024/6/20 19:43:40

PHP 8.4有哪些新功能值得关注

属性钩子（Property Hooks） 允许开发者为每个属性定义自己的get和set钩子，以在属性访问前后添加自定义逻辑。属性钩子通过__get()和__set()方法实现，类似于其他编程语言（如Kotlin、C#和Swift）中的属性访问器…...

编程日记 2024/6/20 19:41:37

PyCharm新手入门

前言 在之前《Python集成开发工具的选择》一文中介绍了python初学者可以使用Jupyter Notebook，Jupyter Notebook简单易用，可以用来练习代码编写，但是实际生产开发环境使用这个工具是远远不够用的，因为实际软件开发中需要软件调试…...

编程日记 2024/6/20 19:39:33

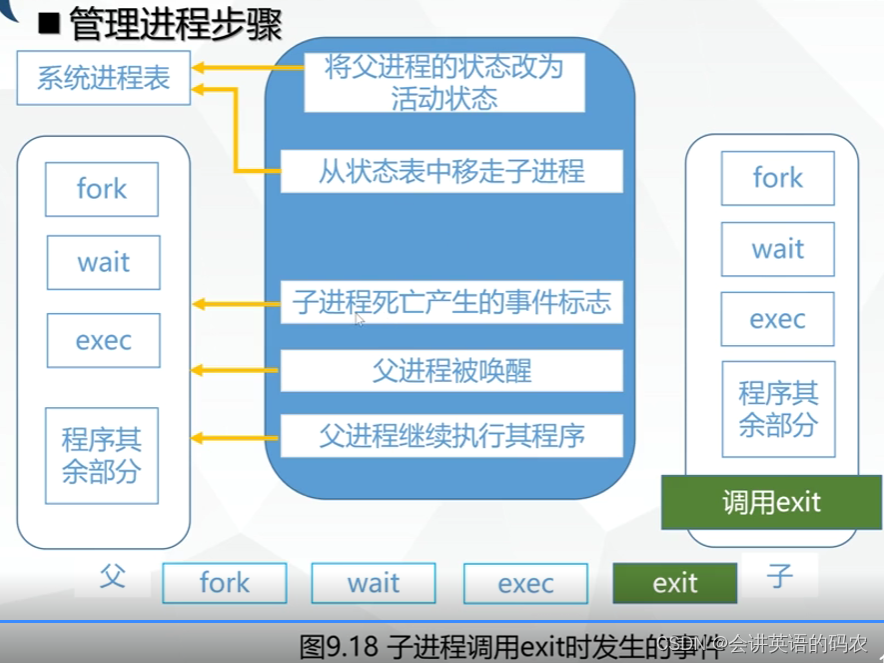
[Linux] 系统管理

全局配置文件 用户个性化配置 配置文件的种类 alias命令和unalias命令 进程管理 进程表...

编程日记 2024/6/20 19:38:31

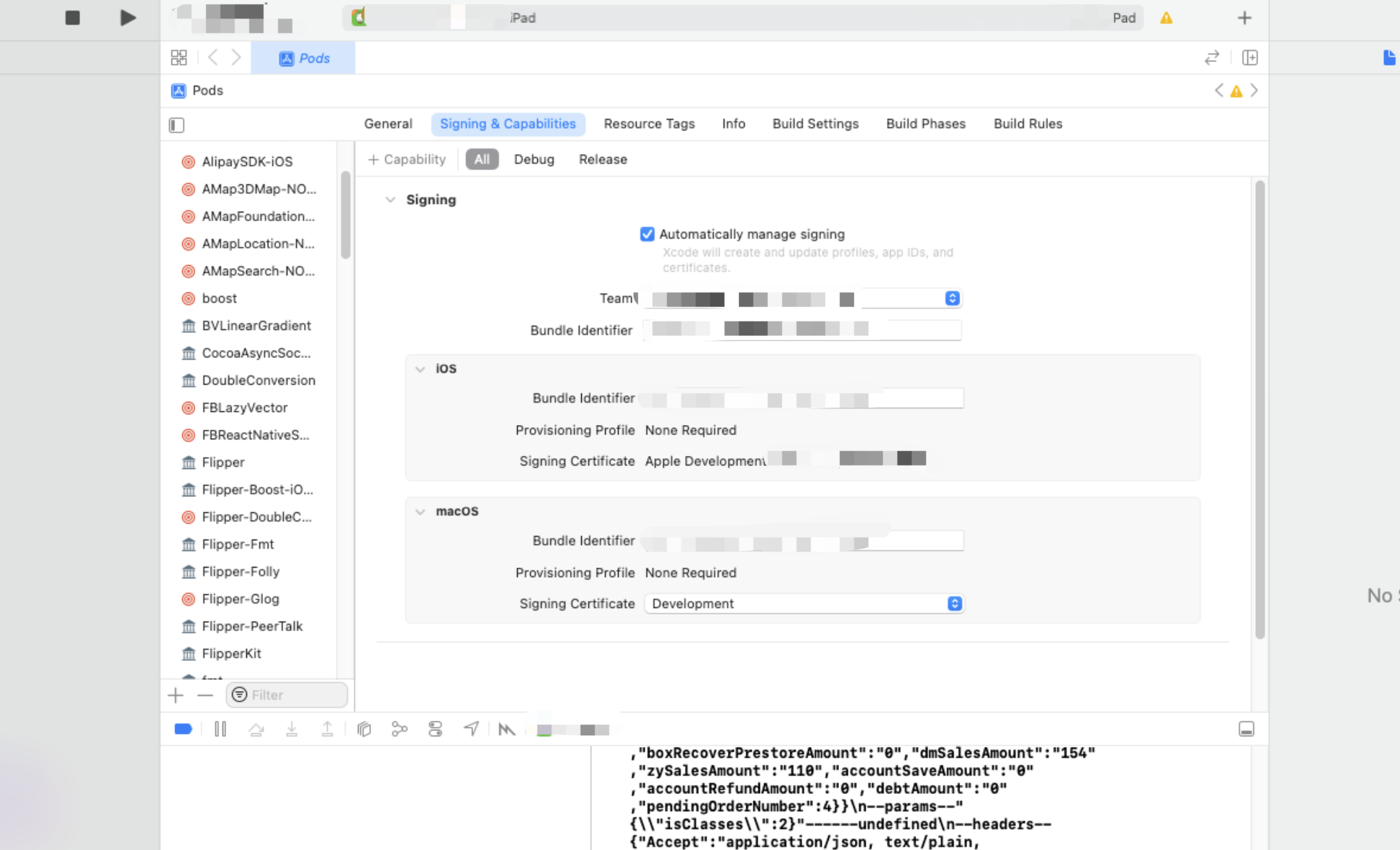
Xcode无法使用设备：Failed to prepare the device for development

问题： Xcode无法使用设备开发，失败报错如下： Failed to prepare the device for development. This operation can fail if the version of the OS on the device is incompatible with the installed version of Xcode. You may also need…...

编程日记 2024/6/20 19:37:30

AWS无服务器 应用程序开发—第十二章 AWS Step Functions

AWS Step Functions 是一种服务，用于协调和管理分布式应用程序中的多个 AWS 服务和 Lambda 函数。它通过创建有状态的工作流来简化和自动化应用程序的各种工作流程，使得复杂的业务逻辑可以以可管理和可调试的方式实现。 主要功能和特点： 状态机定义： 使用 JSON 或 Amazo…...

编程日记 2024/6/20 19:35:27

Linux tcpdump详解

目录 前言：BPF伯克利包过滤器介绍1.BPF语法（tcpdump语法）2.逻辑运算符3.常用的原子条件1. 协议相关的原子条件2. 地址相关的原子条件3. 端口相关的原子条件4. 网络层和链路层(mac地址）原子条件5. 广播和多播6. VLAN 相关的原子条件…...

编程日记 2024/6/20 19:34:26

vue2实现打印功能（vue-print-nb的实现）

实现效果&#xff1a; 引入插件 npm install vue-print-nb --save import Print from vue-print-nb Vue.use(Print) <div ref"printTest" id"printTest"><div style"text-align: center; page-break-after: always"><div style…...

编程日记 2024/6/20 19:30:21

某全国增值税发票查验平台 接口JS逆向

注意&#xff0c;本文只提供学习的思路&#xff0c;严禁违反法律以及破坏信息系统等行为&#xff0c;本文只提供思路 本文的验证码网址如下&#xff0c;使用base64解码获得 aHR0cHM6Ly9pbnYtdmVyaS5jaGluYXRheC5nb3YuY24v 这个平台功能没什么好说的&#xff0c;就是发票查验&am…...

编程日记 2024/6/20 19:28:18

前端练习小项目——视觉冲击卡片

前言&#xff1a; 前言&#xff1a;在学习完HTML和CSS之后&#xff0c;我们就可以开始做一些小项目了&#xff0c;本篇文章所讲的小项目为——视觉冲击卡片 ✨✨✨这里是秋刀鱼不做梦的BLOG ✨✨✨想要了解更多内容可以访问我的主页秋刀鱼不做梦-CSDN博客 先让我们看一下效果&a…...

编程日记 2024/6/20 19:26:15

从0到1：手动测试迈向自动化——手机web应用的自动化测试工具

引言&#xff1a; 在当今移动互联网时代&#xff0c;手机web应用已经成为人们生活中不可或缺的一部分。为了保证手机web应用的质量和稳定性&#xff0c;自动化测试工具变得十分重要。本文将介绍手机web应用自动化测试工具的选择和使用&#xff0c;提供一份超详细且规范的指南&a…...

编程日记 2024/6/20 19:25:14

磁盘未格式化：深度解析、恢复策略与预防措施

一、磁盘未格式化的定义与现象 在计算机存储领域&#xff0c;磁盘未格式化通常指的是磁盘分区或整个磁盘的文件系统信息出现丢失或损坏的情况&#xff0c;导致操作系统无法正确读取和识别磁盘上的数据。当尝试访问这样的磁盘时&#xff0c;系统往往会弹出一个警告框&#xff0…...

编程日记 2024/6/20 19:24:13

Qwen2在Java项目中如何实现优雅的Function_Call工具调用

在当今AI技术飞速发展的背景下&#xff0c;大语言模型如Qwen2和GLM-4凭借其强大的语言处理能力&#xff0c;在诸多领域展现出了巨大的潜力。然而&#xff0c;大模型并非全知全能&#xff0c;它们在处理特定任务时&#xff0c;尤其是在需要与外部系统交互或执行具体功能时&#…...

编程日记 2024/6/20 19:21:08

【SPIE独立出版 | 往届均已完成EI检索】2024云计算、性能计算与深度学习国际学术会议(CCPCDL 2024)

2024云计算、性能计算与深度学习国际学术会议(CCPCDL 2024) 2024 International conference on Cloud Computing, Performance Computing and Deep Learning *CCPCDL往届均已完成EI检索&#xff0c;最快会后4个半月完成&#xff01; 一、重要信息 大会官网&#xff1a;www…...

编程日记 2024/6/20 19:19:05

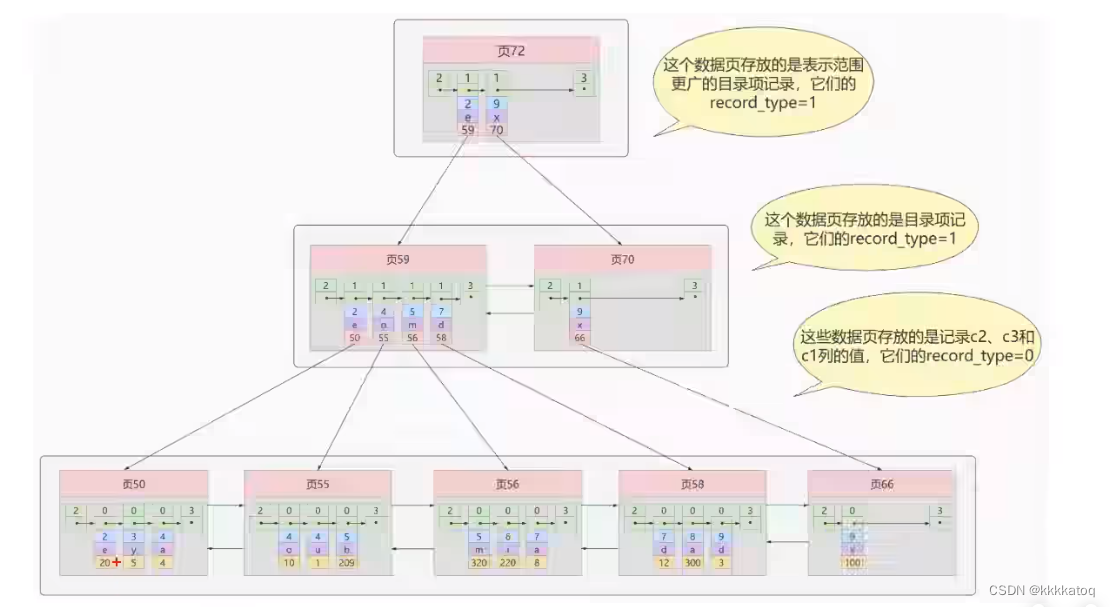
MYSQL 四、mysql进阶 4（索引的数据结构）

一、为什么使用索引 以及 索引的优缺点 1.为什么使用索引 索引是存储引擎用于快速找到数据记录的一种数据结构&#xff0c;就好比一本教科书的目录部分&#xff0c;通过目录中找到对应文章的页码&#xff0c;便可快速定位到需要的文章。Mysql中也是一样的道理&#xff0c;进行数…...

编程日记 2024/6/20 19:18:03

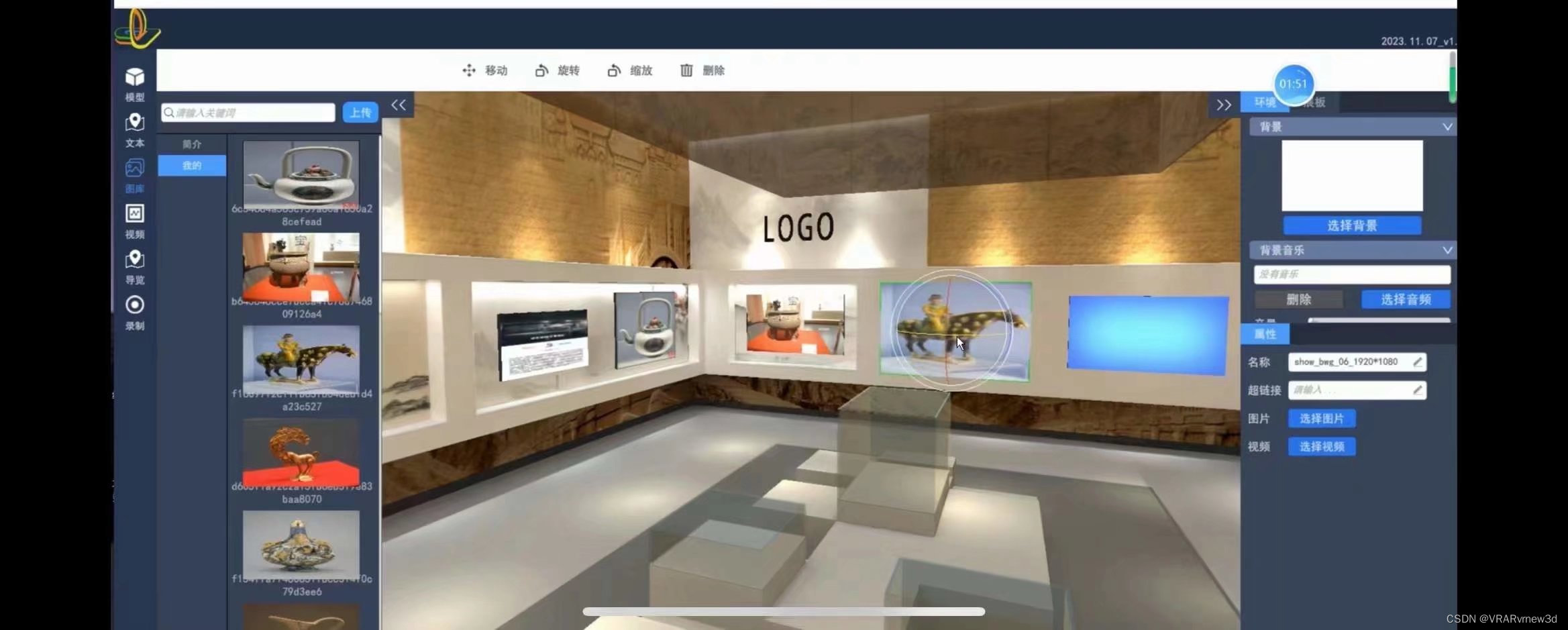
360vr党建线上主题展立体化呈现企业的文化理念和品牌形象

在现代科技的引领下&#xff0c;艺术与VR虚拟现实技术相融合必将成为趋势&#xff0c;深圳VR公司华锐视点荣幸地推出VR艺术品虚拟展厅&#xff0c;为您带来前所未有的艺术观赏体验。体验者足不出户即可置身于一个充满创意与灵感的虚拟艺术空间。 我们深入了解每一位客户的需求与…...

编程日记 2024/6/20 19:16:00

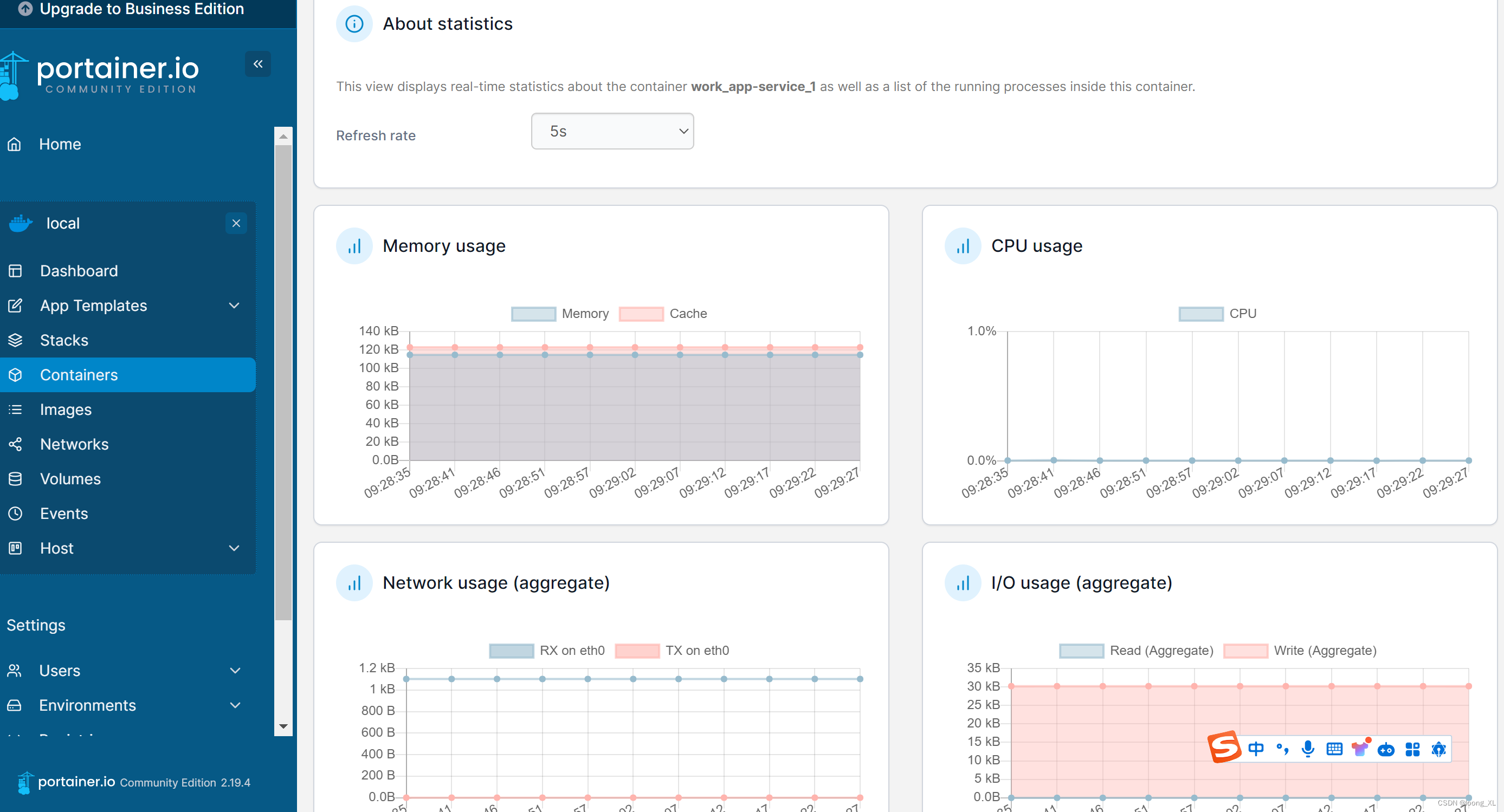
docker通过容器id查看运行命令；Portainer监控管理docker容器

1、docker通过容器id查看运行命令 参考&#xff1a;https://blog.csdn.net/a772304419/article/details/138732138 docker inspect 运行镜像id“Cmd”: [ “–model”, “/qwen-7b”, “–port”, “10860”, “–max-model-len”, “4096”, “–trust-remote-code”, “–t…...

编程日记 2024/6/20 19:14:58

XMind 2024软件最新版下载及详细安装教程

​人所共知的是XMind 在公司和教育领域都有很广泛的应用&#xff0c;在公司中它能够用来进行会议管理、项目管理、信息管理、计划和XMind 被认为是一种新一代演示软件的模式。也就是说XMind不仅能够绘制思维导图&#xff0c;还能够绘制鱼骨图、二维图、树形图、逻辑图、组织结构…...

编程日记 2024/6/20 19:13:57

代码随想录算法训练营第四十四天 | 322. 零钱兑换、279.完全平方数、139.单词拆分、多重背包理论基础、背包问题总结

322. 零钱兑换 题目链接&#xff1a;https://leetcode.cn/problems/coin-change/ 文档讲解&#xff1a;https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html 视频讲解&#xff1a;https://www.bilibili.com/video/BV14K411R7yv/ 思路 确定dp数组以及下…...

编程日记 2024/6/20 19:12:55

开源AGV调度系统OpenTCS中的路由器(router)详解

OpenTCS中的任务分派器router详解 1. 引言2. 路由器(router)2.1 代价计算函数&#xff08;Cost functions&#xff09;2.2 2.1 Routing groups2.1 默认的停车位置选择2.2 可选停车位置属性2.3 默认的充电位置选择2.4 即时运输订单分配 3. 默认任务分派器的配置项4. 参考资料与源…...

编程日记 2024/6/20 19:11:54

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

关于nvm与node.js

1 安装nvm 安装过程中手动修改 nvm的安装路径&#xff0c; 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解&#xff0c;但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后&#xff0c;通常在该文件中会出现以下配置&…...

编程新知 2026/1/28 15:17:32

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案

问题描述&#xff1a;iview使用table 中type: "index",分页之后 &#xff0c;索引还是从1开始&#xff0c;试过绑定后台返回数据的id, 这种方法可行&#xff0c;就是后台返回数据的每个页面id都不完全是按照从1开始的升序&#xff0c;因此百度了下&#xff0c;找到了…...

编程新知 2026/1/29 20:58:41

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/8/9 0:31:20

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2026/2/1 4:14:14

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

编程新知 2026/1/27 16:41:02

Springboot社区养老保险系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;社区养老保险系统小程序被用户普遍使用&#xff0c;为方…...

编程新知 2026/1/26 2:48:53

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表

设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程，两张表是相同的结构，都有整型主键id字段，需要每次从数据库分批取得2000条数据，用于比较，比较操作的同时可以再取2000条数据，等上一次比较完成之后，开始比较，直到比较完所有的数据。比较操作需要比较…...

编程新知 2025/9/14 5:35:46