红黑树(数据结构篇)
数据结构之红黑树
红黑树(RB-tree)
概念:
- 红黑树是AVL树的变种,它是每一个节点或者着成红色,或者着成黑色的一棵二叉查找树。
- 对红黑树的操作在最坏情形下花费O(logN)时间,它的插入操作使用的是非递归形式实现
- 红黑树的高度最多是2log(N+1)
特性:
- 红黑树是具有着色性质的二叉查找树,也就意味着树的节点值是有序的,且每个节点只可能是红色或者黑色
- 红黑树的根是黑色的
- 如果一个节点是红色的,那么它的子节点必须是黑色的
- 从一个节点到一个空指针的每一条路径必须包含相同数目的黑色节点
自顶向下插入操作:
-
如果使用自底向上插入的话还需要进行逐步递归是他们保证满足红黑树特性,效率就降低了。
-
令X为新插入节点(在下面的第三操作中为当前节点),P为X的父节点,G为P的父节点(也就是X的祖父节点),GP为G的父节点(也就是P的祖父节点,X的曾祖父节点)
-
因为红黑树是一颗二叉查找树,因此在插入时需要查找要插入的值的正确位置,在这个查找路径中,如果遇到节点(X)为黑色而子节点全部为红色,我们就进行
翻转操作,也就是将该节点(X)着成红色,子节点全部着成黑色。翻转后:如果翻转后发现P和X节点都是红色就需要根据树的结构进行
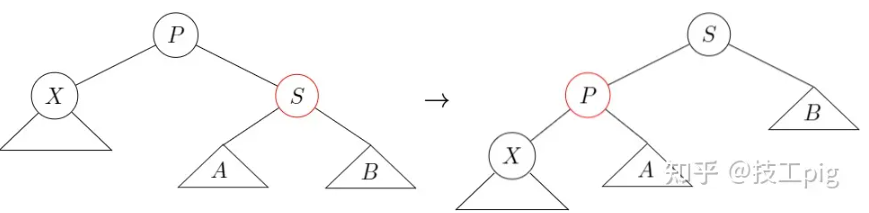
旋转操作- 如果X,P,G形成"一字形",则对P的父节点G(也就是X的祖父节点)与P进行
单旋转,并将新根也就是P着成黑色,新根的子节点都着成红色。 - 如果X,P,G形成"之字形",则对G与X节点进行
双旋转,并将新根着成黑色(也就是X节点),然后将新根的子节点着成红色
- 如果X,P,G形成"一字形",则对P的父节点G(也就是X的祖父节点)与P进行
-
如果该节点(X)是黑色则继续将X下降,直到找到红色节点继续翻转,或者找到指定插入位置,找到指定位置也就是当前节点位置X就进行插入,新节点也是红色,需要重新判断其父节点是否为红色,为红色又需要进行翻转操作来调整。
自顶向下删除操作
-
自顶向下删除也需要保证红黑树的性质,插入是插入一片红色的叶子节点,那么反过来我们删除一个红色叶子节点就不会破坏红黑树性质,自顶向下插入的翻转操作是将红色节点减少,并将红色节点上浮,因为删除是插入的逆过程,因此删除的翻转操作就是要将树中的红色节点增多,并将红色节点下沉,这样我们删除红色叶子节点的概率更大,并且不会破坏红黑树性质
-
删除操作一共有5种情况需要解决
- 要删除节点cur跟其兄弟节点s原本颜色为黑色,父亲节点p为红色
- s的两个儿子都是红色,这样双旋转和单旋转都可以,这里优先选择
ps单选转调整,情况1-case4 - s的左儿子为红色,需要
ps.l双旋转调整(s.l为s的左儿子),情况2-case1 - s的右儿子为红色,需要
ps单旋转调整,情况3-case2 - s有两个黑色儿子,直接
cur,p,s颜色翻转操作调整,情况4-case3 - p和cur为黑色,s为红色,需要
交换sp节点的颜色,并且sp单旋转调整,情况5-case5 - cur为红色,可以继续
将cur下降,也就是当前cur指向原本cur的子节点,如果为红色继续下降,如果为黑色就判断是否需要操作
-
tomove指向要删除节点也就是目标节点,而p指向真正要删除的叶子节点,cur则while循环完后则是指向nil节点,因为将tomove标记完,就进行cur和p就查找tomove右子树的最小值节点进行删除,而while循环终止条件为cur==nil情况,因此p指向真正要删除的节点
-
找到tomove和p后,将tomove的data等于p的data,将p删除,因为p为叶子节点,将p的父节点指向nil。
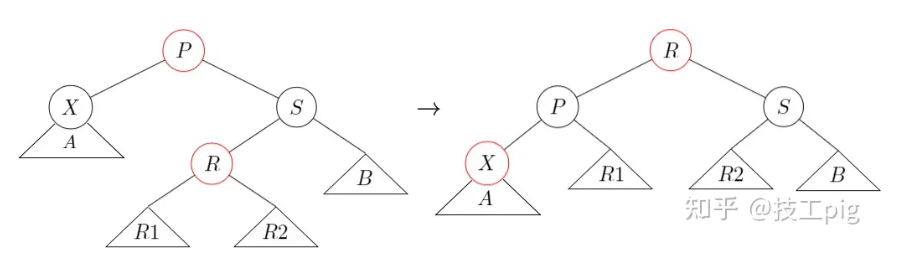 情况2-case1
情况2-case1
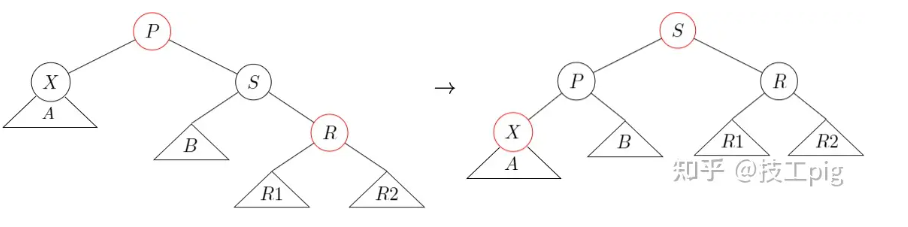 情况3-case2
情况3-case2
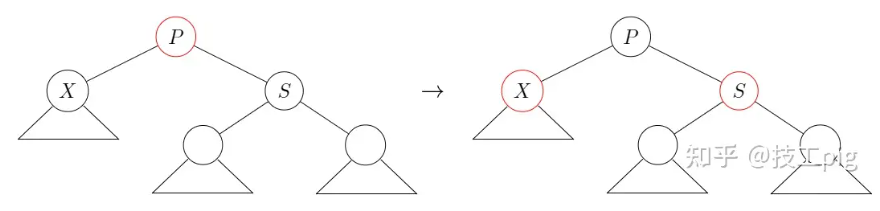 情况4-case3
情况4-case3
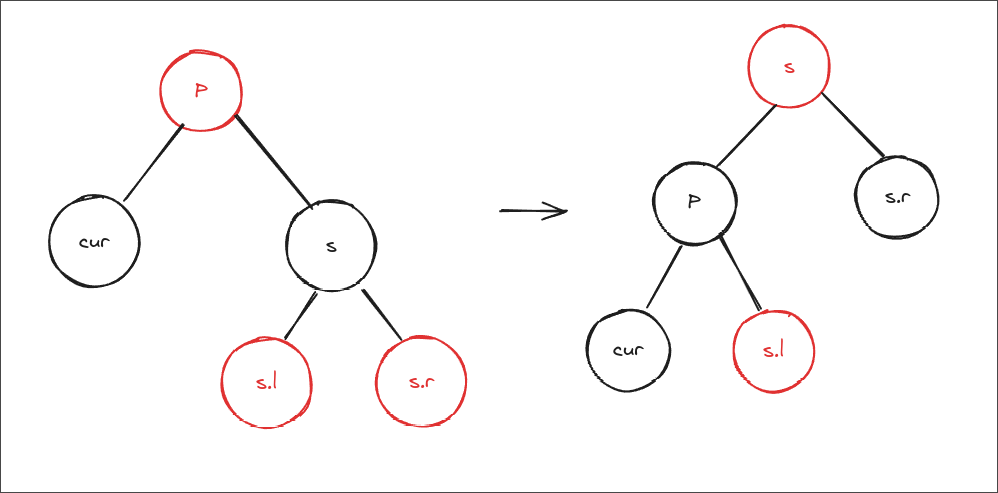 情况1-case4
情况1-case4
 情况5-case5
情况5-case5
计算红黑树层数:
- 需要对log2(树中总共节点数+1)向上取整
代码:
int Height(const int count){return std::ceil(std::log2(count+1));
}
代码实现:
#include <iostream>
#include <queue>
#include <math.h>
#include <limits.h>
using namespace std;typedef enum {red,black} colortype;struct RBNode{int data;RBNode *left,*right,*parent;colortype color; //颜色RBNode(const int val,RBNode* l,RBNode* r,RBNode* p,colortype c=red):data(val),left(l),right(r),parent(p),color(c){};
};class RBtree{
public:RBtree(){nil=new RBNode(INT_MAX, nullptr, nullptr, nullptr,black);root= nullptr;t=new RBNode(INT_MIN,nil,nil,nil,black);size=0;}~RBtree(){clear();delete t;delete nil;};void insert(const int val); //插入操作void del(const int val); //删除操作RBNode* find(const int val); //查找操作void print(); //打印操作,层序遍历//清空操作void clear(){clear(root);root= nullptr;t->right=nil;size=0;}protected:void overturnred(const int val,RBNode* &cur); //翻转操作,将当前节点变成红色,子节点变成黑色void overturnblack(int val,RBNode* &cur); //翻转操作,将当前节点变成黑色,子节点变成红色RBNode* SingleRotatewithleft(RBNode* &k1);RBNode* SingleRotatewithright(RBNode* &k1);RBNode* Rotate(const int val,RBNode* &k1){if(val<k1->data){return k1->left=val<k1->left->data? SingleRotatewithleft(k1->left): SingleRotatewithright(k1->left);}else{return k1->right=val<k1->right->data? SingleRotatewithleft(k1->right): SingleRotatewithright(k1->right);}}void clear(RBNode* &rt);// 计算红黑树层数int Height(int nodeCount) {// 红黑树的层数为 log2(nodeCount+1)return (int)std::ceil(std::log2(nodeCount+1));}
private:RBNode* root;RBNode* nil; //空节点,color为黑色RBNode* t; //根标记,用于删除操作的便捷int size;
};RBNode* RBtree::SingleRotatewithleft(RBNode *&k1) {RBNode* k2;k2=k1->left;k1->left=k2->right;k2->right=k1;return k2;
}RBNode* RBtree::SingleRotatewithright(RBNode *&k1) {RBNode* k2;k2=k1->right;k1->right=k2->left;k2->left=k1;return k2;
}//翻转操作
void RBtree::overturnred(const int val,RBNode* &cur) {cur->color=red;cur->left->color=cur->right->color=black;RBNode* p=cur->parent;if(p->color==red){RBNode* g=p->parent;g->color=red;if((val<g->data)!=(val<p->data)){ //双旋转p= Rotate(val,g);}cur= Rotate(val,g->parent);cur->color=black;}root->color=black;
}//插入操作
void RBtree::insert(const int val) {if(root== nullptr){root=new RBNode(val,nil,nil, t,black);t->right=root;size++;return;}RBNode *cur,*p;cur=p=root;while (cur!=nil){p=cur;if(cur->left->color==red&&cur->right->color==red){overturnred(val,cur);}cur=val<p->data?p->left:p->right;}if(cur!=nil){return;}cur=new RBNode(val, nil, nil, p);if(val<p->data){p->left=cur;}else{p->right=cur;}overturnred(val,cur);size++;
}void RBtree::overturnblack(int val, RBNode *&cur) {cur->color=red;RBNode* p=cur->parent;RBNode* s=val<p->data?p->left:p->right;//case4:要删除节点cur跟其兄弟节点s原本颜色为黑色,父亲节点p为红色,s的两个儿子都是红色,这样双旋转和单旋转都可以,这里优先选择ps单选转//case2:要删除节点cur跟其兄弟节点s原本颜色为黑色,父亲节点p为红色,s的右儿子为红色情况,需要ps单旋转调整if(s->right->color==red){val=s->right->data;}//case1:要删除节点cur跟其兄弟节点s原本颜色为黑色,父亲节点p为红色,s的左儿子为红色的情况,需要ps.l双旋转调整else if(s->left->color==red){val=s->left->data;}//case3:要删除节点cur跟其兄弟节点s原本颜色为黑色,父亲节点p为红色,s有两个黑儿子(nil节点也是黑色),直接将颜色翻转即可else{//翻转操作if(s!=nil){s->color=red;}p->color=black;return;}if((val<s->data)!=(val<p->data)){Rotate(val,p);}RBNode* g=p->parent;Rotate(val,g);//将调整完的cur的新祖父也就是s或者s的左儿子变成红色,也就是删除完cur后将颜色调整到之前cur在翻转前的情况g->color=red;g->left->color=g->right->color=black;
}void RBtree::del(const int val) {RBNode* tomove=nil; //找到删除节点RBNode *g,*p,*s,*cur;g=p=t,s=t->left,cur=root;while (cur!=nil){//翻转颜色if(cur->left->color==black&&cur->right->color==black){overturnblack(val,cur);}else{g=p;p=cur;if(val<p->data){cur=p->left,s=p->right;}else{tomove=cur,cur=p->right,s=p->left;}//case5:此时肯定p和cur都为黑色,因为如果p为红色早就翻转了,s肯定是红色,将s变成黑色,p变为红色,sp单旋转调整if(cur->color==black){s->color=black;p->color=red;//单旋转完,cur新祖父变为s,将s重新更改g= Rotate(val,g);s=val<p->data?p->left:p->right;//调整完该情况就重新检查上述操作continue;}//else,cur一定为红色,则可以直接继续将cur继续下降}g=p;p=cur;if(val<p->data){cur=p->left,s=p->right;}else{tomove=cur,cur=p->right,s=p->left;}}root->color=black; //保证红黑树性质2不被破坏,也就是根一定为黑色//判断是否找到真正要删除的节点,如果找不到就退出if(tomove==nil&&tomove->data!=val){cout<<"未找到要删除对应值的节点";return;}//tomove是要删除的节点,而p指向的是真正要删除的节点tomove->data=p->data;if(g->left==p) g->left=nil;else g->right=nil;delete p;size--;
}RBNode* RBtree::find(const int val) {if(root!= nullptr){RBNode* cur=root;while (cur!=nil){if(cur->data==val) return cur;cur=val<cur->data?cur->left:cur->right;}if(cur==nil){cout<<"树中没有指定值节点"<<endl;}}return root;
}void RBtree::print() {if(root== nullptr){cout<<"树为空"<<endl;return;}queue<RBNode*>q;q.push(root);int cnt=1;int ans=0;int h= Height(size);while (!q.empty()){if(ans==h+1) break;RBNode* cur=q.front();q.pop();if(cur== nullptr){cout<<"null"<<" ";continue;}q.push(cur->left);q.push(cur->right);if(cur->color==red){cout<<"\033[31m"<<cur->data<<"\033[0m"<<" ";}else if(cur==nil) cout<<"nil"<<" ";else cout<<cur->data<<" ";if(cnt==pow(2,ans)){cout<<endl;cnt=0,ans++;}cnt++;}return;
}void RBtree::clear(RBNode* &rt) {if(rt!=nil){clear(rt->left);clear(rt->right);delete rt;rt=nil;}return;
}int main() {RBtree rBtree;rBtree.insert(30);rBtree.insert(15);rBtree.insert(65);rBtree.insert(10);rBtree.insert(20);rBtree.insert(5);rBtree.insert(60);rBtree.insert(70);rBtree.insert(50);rBtree.insert(64);rBtree.insert(66);rBtree.insert(85);rBtree.insert(40);rBtree.insert(55);rBtree.insert(63);rBtree.insert(80);rBtree.insert(90);rBtree.insert(45);rBtree.del(65);rBtree.del(50);rBtree.del(30);rBtree.print();return 0;
}
尾言
完整版笔记也就是数据结构与算法专栏完整版可到我的博客进行查看,或者在github库中自取(包含源代码)
- 博客1: codebooks.xyz
- 博客2:moonfordream.github.io
- github项目地址:Data-Structure-and-Algorithms
相关文章:

红黑树(数据结构篇)
数据结构之红黑树 红黑树(RB-tree) 概念: 红黑树是AVL树的变种,它是每一个节点或者着成红色,或者着成黑色的一棵二叉查找树。对红黑树的操作在最坏情形下花费O(logN)时间,它的插入操作使用的是非递归形式实现红黑树的高度最多是…...
)
高级视频编码器性能对比(H265、VP9、AV1)
1、背景介绍 目前在视频编解码器中,H264已经成为绝对的主流,被大部分设备、浏览器所支持。虽然有更先进的编码器推出,但是受限于推广速度和设备支持成本,一直未能成为主流。 今年公司目标是持续降本增效,现在将”屠刀…...
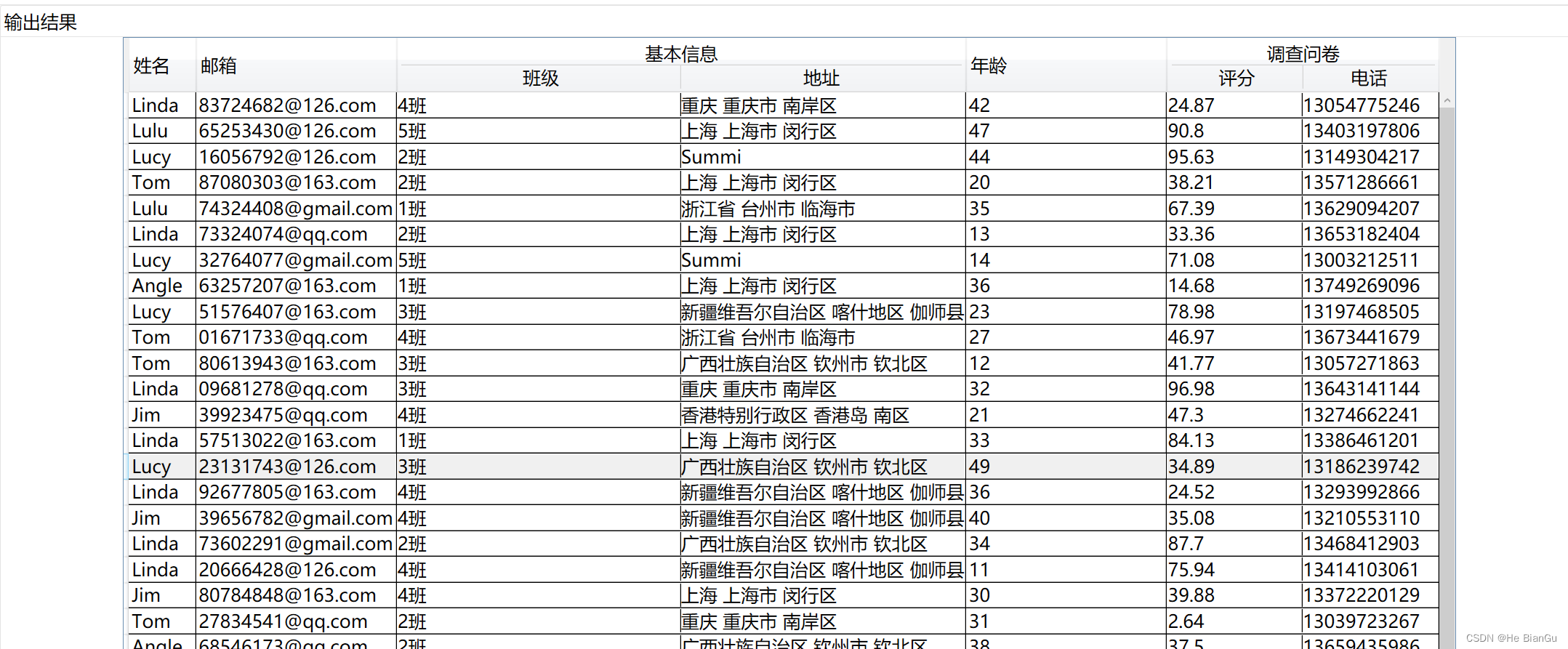
示例:WPF中DataGrid简单设置合并列头
一、目的:应用DataGridTemplateColumn列模板,去拆分列头和单元格布局的方式设置列头合并样式 二、实现 效果如下 三、环境 VS2022 四、示例 应用DataGridTemplateColumn自定义列头信息和单元格信息 <DataGrid AutoGenerateColumns"False"…...
Matlab图像处理——细胞图像的分割和计数显示
一. 项目介绍 使用MATLAB编写的细胞图像分割及计数系统,实现了对图像内细胞的计数,以及对每个细胞周长和面积的测量,并分别展示了分割后的每个细胞的图像。实验步骤共分为图像预处理、图像预分割、空洞填充、黏连细胞分割、细胞个数统计、细胞…...

六爻排盘神机
选修课留了3000字的论文......确实,削微有那么一点小困难…… 但是,倘若我拿出已经占了6419个字符的 “六爻排盘神机” ,阁下…应该…不会…骂我吧 且看,六爻排盘神机! import random import datetime from lunarcale…...

【ARMv8/v9 GIC 系列 2.1 -- GIC SPI 中断的 pending 和 clear pending 配置】
文章目录 GIC Pending 和 Clear PendingGICD_ISPENDR<n>GICD_ICPENDR<n>参数<n>编号解释使用举例设置中断ID 100为挂起状态清除中断ID 100的挂起状态 代码实现小结 GIC Pending 和 Clear Pending 在ARMv8体系结构中,GICD_ISPENDR<n> 和 GI…...
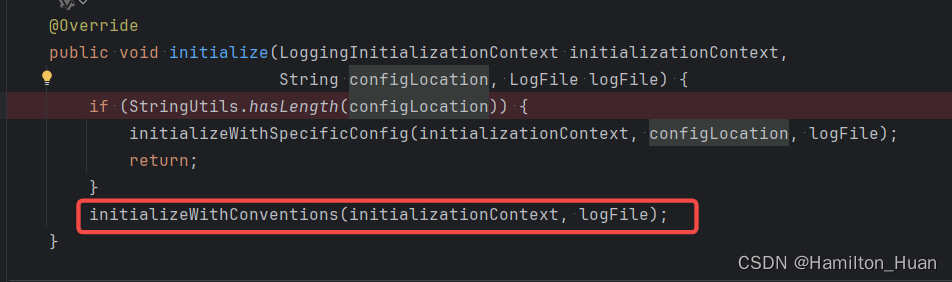
SpringBoot集成logback初始化源码解析(部分)
一.SpringBoot配置扩展点 SpringBoot日志模块使用监听的方式进行初始化,在SpringBoot项目启动后,会通知日志监听器 在日志监听器中ApplicationStartingEvent事件用来确定到底使用哪个日志系统,logback log4j等 在日志监听器中ApplicationEn…...
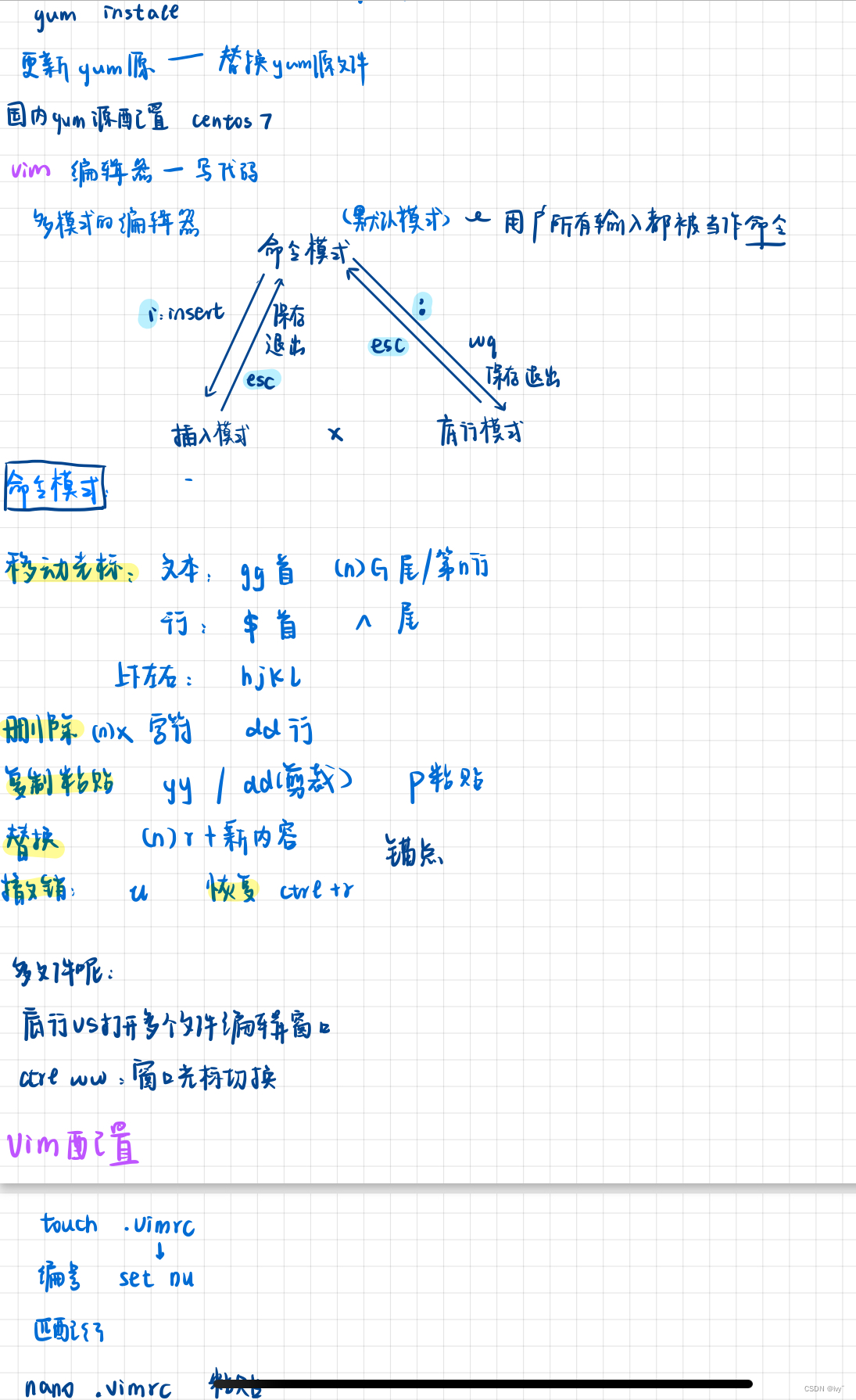
【Linux工具】yum软件包管理器与Vim编辑器的高效运用
目录 Linux 软件包管理器 YUM 什么是软件包 安装工具 rzsz 及注意事项 查看软件包 安装和卸载软件 安装软件 卸载软件 Linux 开发工具 编辑器 - Vim 使用 编辑 Vim 与 Vi 的区别 Vim 的基本概念 三种模式 Vim 的基本操作 操作尝试: Vim 命令集解释…...

Matlab数学建模实战应用:案例4 - 图像处理
目录 前言 一、图像处理基础 二、Matlab图像处理工具箱 三、案例:图像锐化、去噪和分割 步骤 1:读取和显示图像 步骤 2:图像锐化 步骤 3:图像去噪 步骤 4:图像分割 完整代码示例 四、实际应用 实例总结 总…...
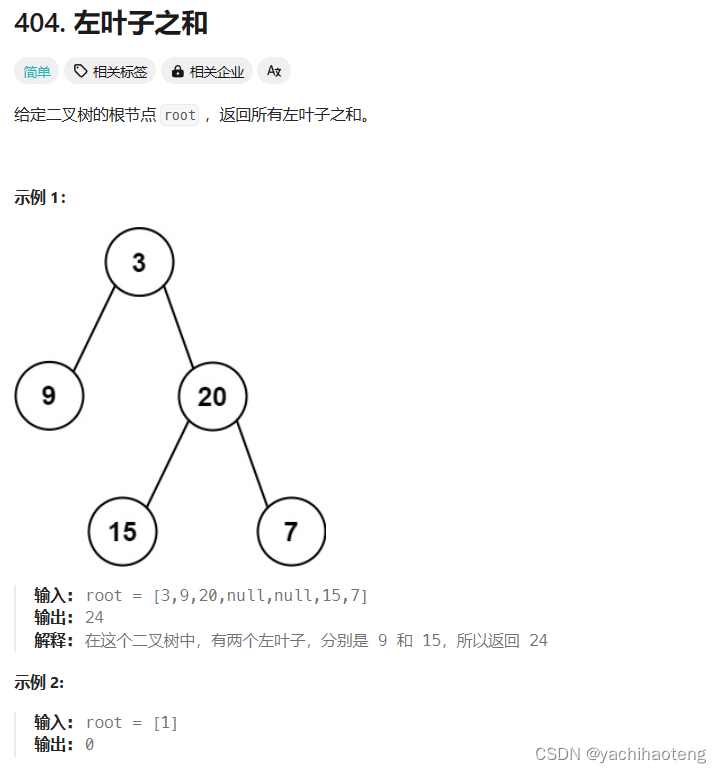
Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C 目录 257.完全二叉树的节点个数 110.平衡二叉树 257.二叉树的所有路径 404.左叶子之和 总结 257.完全二叉树的节点个数 文档讲解:代码随想录完全二叉树的节点个数 视频讲解…...

Python 基础:异常
目录 一、异常概念二、处理异常2.1 抛出异常2.2 使用 try-except 代码块2.3 使用 try-except-else 代码块2.4 静默失败 三、总结 遇到看不明白的地方,欢迎在评论中留言呐,一起讨论,一起进步! 本文参考:《Python编程&a…...

XML 应用程序
XML 应用程序 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。它是一种自我描述的语言,允许用户定义自己的标签和文档结构。XML广泛应用于各种应用程序中,包括网站开发、数据交换、文档管理等。本文将探讨XML的一些主要…...

SprringCloud Gateway动态添加路由不重启
文章目录 前言:一、动态路由必要性二、SpringCloud Gateway路由加载过程RouteDefinitionLocator接口PropertiesRouteDefinitionLocator类DiscoveryClientRouteDefinitionLocatorInMemoryRouteDefinitionRepositoryCompositeRouteDefinitionLocator类CachingRouteDef…...
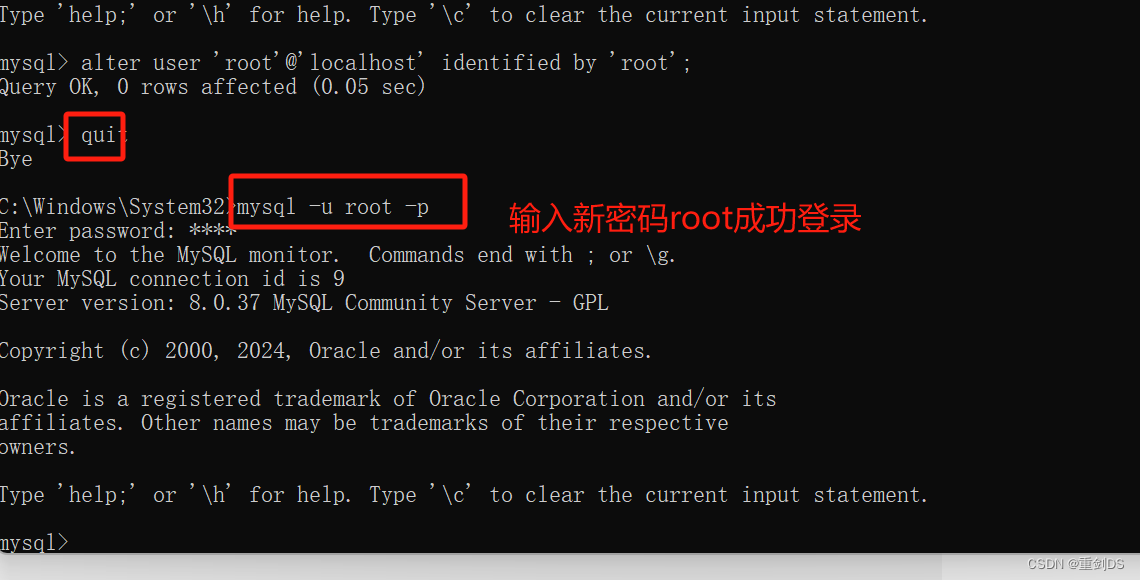
Windows安装mysql
首先去官网下载社区版本的mysql(如果连不上,挂梯子) https://www.mysql.com/downloads/ 2. 去配置环境变量path 3. 在cmd里面初始化数据库(在搜索框输入cmd,或者在资源管理器下搜索烂输入cmd回车就行) my…...
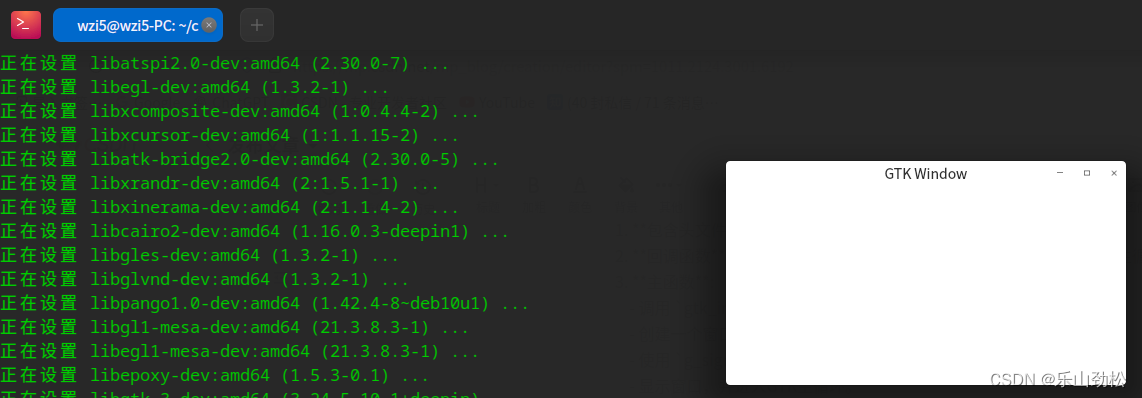
chatgpt: linux 下用纯c 编写ui
在Linux下用纯C语言编写用户界面(UI),通常会使用GTK或Xlib。GTK是一个更高级的库,提供了丰富的控件和功能,而Xlib则是一个更底层的库,提供了直接操作X Window系统的功能。 下面是一个使用GTK在Linux上创建…...

Java十六进制Dump打印数据
代码 package test;import java.io.IOException;import sun.misc.HexDumpEncoder;@SuppressWarnings("restriction")...
某棋牌渗透测试
前言 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一、信息收集 这里通过fofa进行收集,语法为:body某棋牌 && titlexxx 图1-1 fofa资产收集 …...
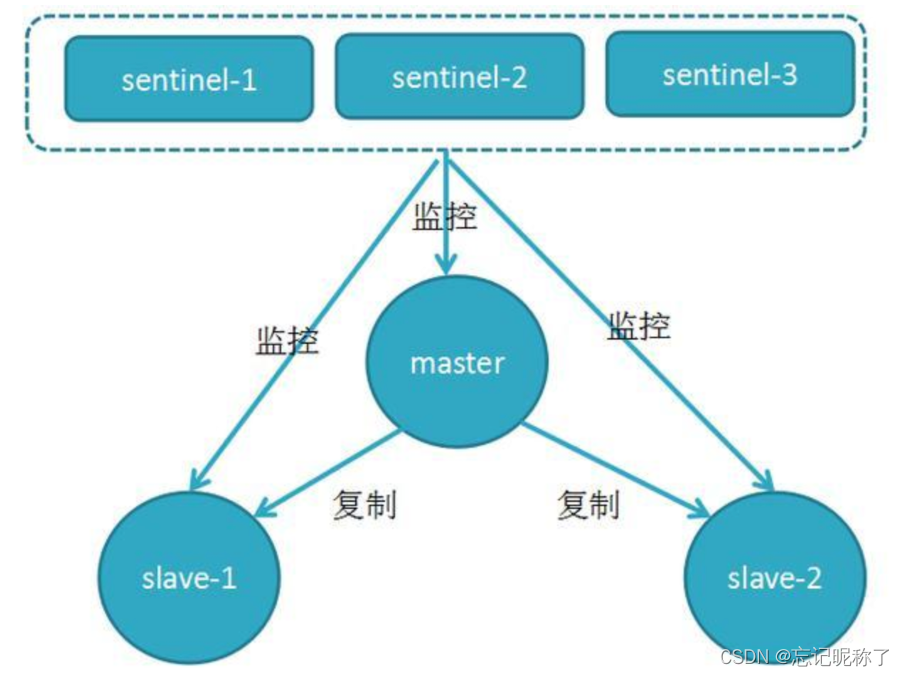
JAVA面试(六)
缓存 MemcachedredisRedis常见数据类型和使用Redis缓存持久化RDB-快照AOF-追加文件 Redis数据过期机制惰性删除定期删除Redis缓存淘汰策略(8种)算法LRU (Least Recently Used):最近最少使用LFU(Least Frequ…...

【C语言】手写学生管理系统丨附源码+教程
最近感觉大家好多在忙C语言课设~ 我来贡献一下,如果对你有帮助的话谢谢大家的点赞收藏喔! 1. 项目分析 小白的神级项目,99%的程序员,都做过这个项目! 掌握这个项目,就基本掌握 C 语言了! 跳…...

流媒体传输协议HTTP-FLV、WebSocket-FLV、HTTP-TS 和 WebSocket-TS的详细介绍、应用场景及对比
一、前言 HTTP-FLV、WS-FLV、HTTP-TS 和 WS-TS 是针对 FLV 和 TS 格式视频流的不同传输方式。它们通过不同的协议实现视频流的传输,以满足不同的应用场景和需求。接下来我们对这些流媒体传输协议进行剖析。 二、传输协议 1、HTTP-FLV 介绍:基于 HTTP…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
