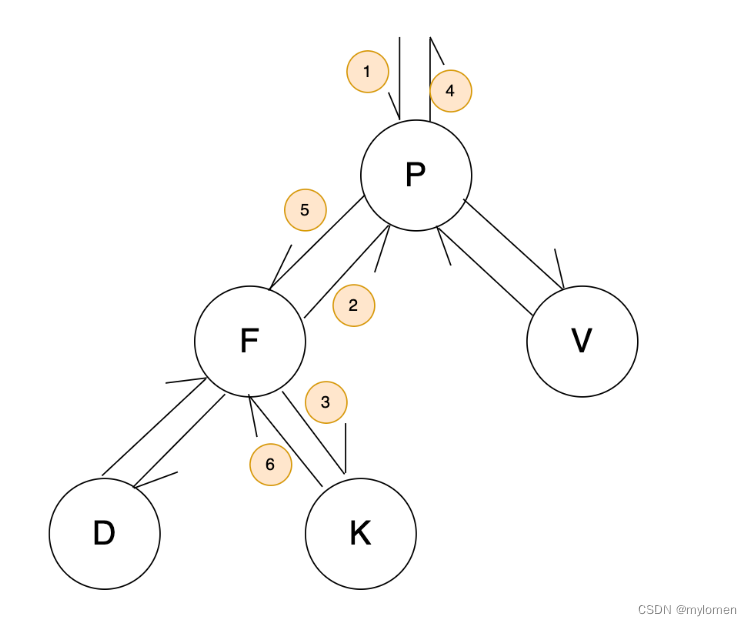
从2-3-4树开始理解红黑二叉树(JAVA代码手撸版)
经典的红黑二叉树在新增/删除数据时维持自平衡始终对应着一个2-3-4 树。本文只关注2-3-4 对应的经典红黑二叉树。
暂时不考虑 2-3 树对应的左倾红黑二叉树。
背景知识
2-3-4 树简介
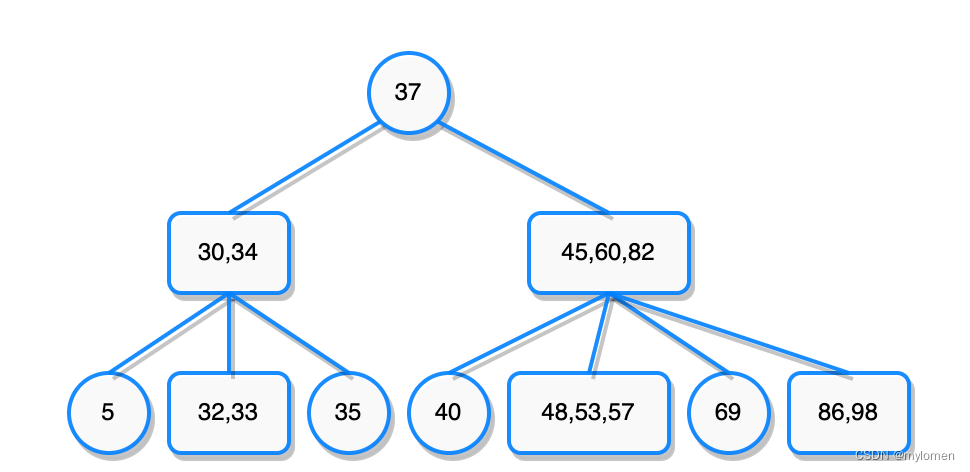
一棵 2-3-4 树的结点分为 内部结点 (internal nodes) 和 叶子结点 (leaf nodes) ,定义如下。
内部结点:
-
2-结点: 拥有1个数据项x,2个子结点。
- 左子树中任意结点数据项均小于x。
- 右子树中任意结点数据项均大于x。
-
3-结点: 拥有2个数据项x,y,3个子结点。
- 左子树中任意结点数据项均小于x。
- 中间子树中任意结点数据项均介于x与y之间。
- 右子树中任意结点数据项均大于y。
-
4-结点: 拥有3个数据项x,y,z,4个子结点。
- 左子树中任意结点数据项均小于x。
- 左侧中间子树中任意结点数据项均介于x与y之间。
- 右侧中间子树中任意结点数据项均介于y与z之间。
- 右子树中任意结点数据项均大于z。
-
叶子结点: 无子结点,数据项为 1 项或 2 项或 3项。
2-3-4 树节点变换
插入操作一定是插入叶子节点中,然后根据情况进行调整。
| 情形 | 具体过程 |
|---|
(该结点为根结点)4-结点先分解为3个2-结点后 (树高+1) 再插入。 3.插入至4-结点中
(父结点为2-结点)4-结点先分解为3个2-结点,其中一个与父结点合并,使得父结点变为3-结点,然后再插入。 4.插入至4-结点中
(父结点为3-结点)4-结点先分解为3个2-结点,其中一个与父结点合并,使得父结点变为4-结点,然后再插入。 5.插入至4-结点中
(父结点为4-结点) 与上一条类似,但父结点变为5-结点,继续向上 (送入一个结点后) 分解直到:
1. 遇到2-结点或3-结点,转变为情形1。
2. 遇到4-结点,继续上送。
3. 到根处仍为4-结点,转变为情形2。
红黑树5条性质
| 五大性质 | 描述 |
|---|---|
| 1. 颜色 | 红黑树的结点或者为黑色或者为红色。 |
| 2. 根结点 | 根结点为黑色。 |
| 3. null结点 | 叶子结点的null子结点(上图未画出,通常都不会画出)为黑色。 |
| 4. 不可连续红 | 红色结点的子结点为黑色。 |
| 5. 完美黑平衡 | 红黑树是「完美黑平衡」的,即任意叶子结点到根结点所经过的黑链数相同。 |
左旋
以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。
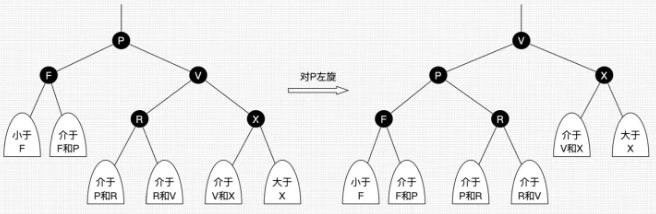
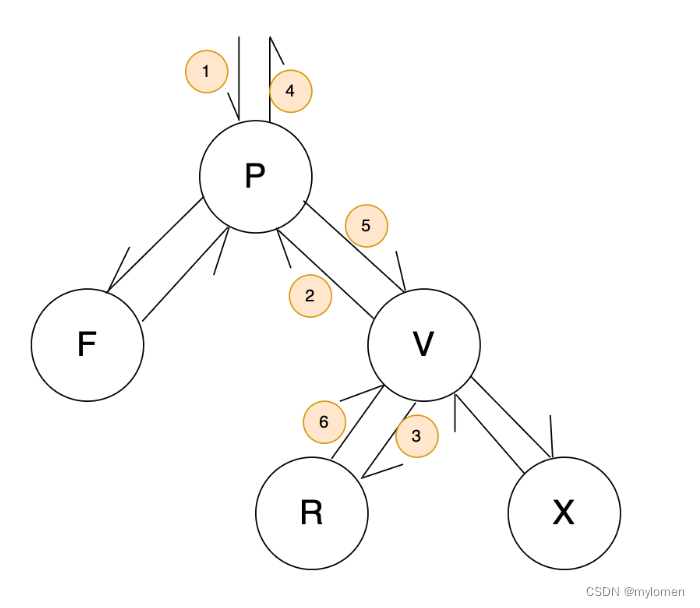
java 代码实现如下(带图解)
/**** @param p*/
void rotate_left(RbNode p) {// 1.处理当前节点的父节点if (p.parent == null) {this.root = p.right;//1} else if (p.parent.left != null && p.parent.left.val == p.val) {p.parent.left = p.right;//1} else {p.parent.right = p.right;//1}// 2.处理历史右子节点。(当前父节点)p.right.parent = p.parent;//2RbNode rightLeftNode = p.right.left;p.right.left = p;//3// 3. 处理当前节点p.parent = p.right;//4p.right = rightLeftNode;//5// 4.处理历史右节点的左子节点if (rightLeftNode != null) {rightLeftNode.parent = p;//6}
}
右旋
以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
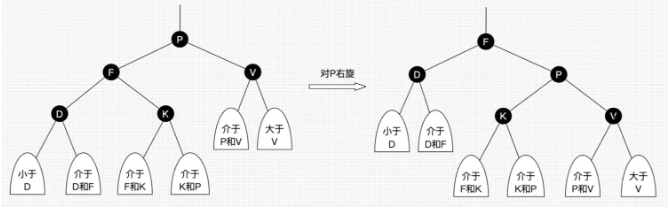
java 代码实现如下(可优化)
/**** @param p*/
void rotate_right(RbNode p) {// 1.处理当前节点的父节点if (p.parent == null) {this.root = p.left;//1} else if (p.parent.left != null && p.parent.left.val == p.val) {p.parent.left = p.left;//1} else {p.parent.right = p.left;//1}// 2.处理历史左子节点。(当前父节点)p.left.parent = p.parent;//2RbNode leftRightNode = p.left.right;p.left.right = p;//3// 3. 处理当前节点p.parent = p.left;//4p.left = leftRightNode;//5// 4.处理历史左节点的右子节点if (leftRightNode != null) {leftRightNode.parent = p;//6}
}
查询某节点的后继节点
依据二叉树中序遍历,查找当前节点的后续节点(寻找继承人)
RbNode findSuccessorNode(RbNode curNode) {if (curNode == null) {return null;}//1. 向下搜索-> 当前节点有 右子节点(红黑二叉树删除节点只使用到这里逻辑).if (curNode.right != null) {RbNode mySuccessorNode = curNode;while (mySuccessorNode.left != null) {mySuccessorNode = mySuccessorNode.left;}return mySuccessorNode;}//2. 向上搜索-> 当前节点没有 右子节点.RbNode parent = curNode.parent;//如果没有父节点,则当前节点是root节点,直接返回nullif (parent == null) {return null;}//如果当前节点是父节点的左子节点,则当前节点的后继节点就是 父节点if (parent.left == curNode) {return parent;}//向上搜索当前节点的父节点...中的第一个左节点while (parent.parent != null && parent.parent.right == parent) {parent = parent.parent;}return parent.parent;
}
关于黑色节点
子节点为空页当作黑色节点
关于插入节点
插入节点一定是红色,且一定插入在叶子节点,然后根据情况去调整二叉树平衡状态。
关于删除节点
删除节点最终一定是删除叶子节点,如果删除的不是叶子节点,需要发现待删除节点的后继节点(必然在叶子节点),然后替换之后再删除。最后根据场景调整。
在线模拟红黑二叉树地址
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
红黑二叉树插入节点
红黑二叉树插入节点与 2-3-4 树插入节点对照来理解。主要有三种 2-节点插入节点;3-节点插入节点;4-节点插入节点。
插入2-结点 (2变3)
若在一黑结点下插入,且该黑结点没有红子结点时,那么这个黑结点就代表了2-结点,也就是此时我们会将 x 插入一个2-结点,因此x可直接插入,不需要调整。
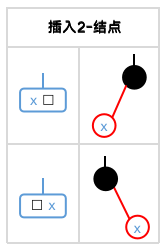
插入3-结点 (3变4)
- 若在一红色结点下插入,且该红结点不存在红色兄弟结点时,那么这个红结点就代表了3-结点 (与它的黑父结点构成3-结点)
,因此x可直接插入此3-结点。 - 若在一黑色结点下插入,则为左下和右上两种「^」情形,也属于插入3-结点情形。
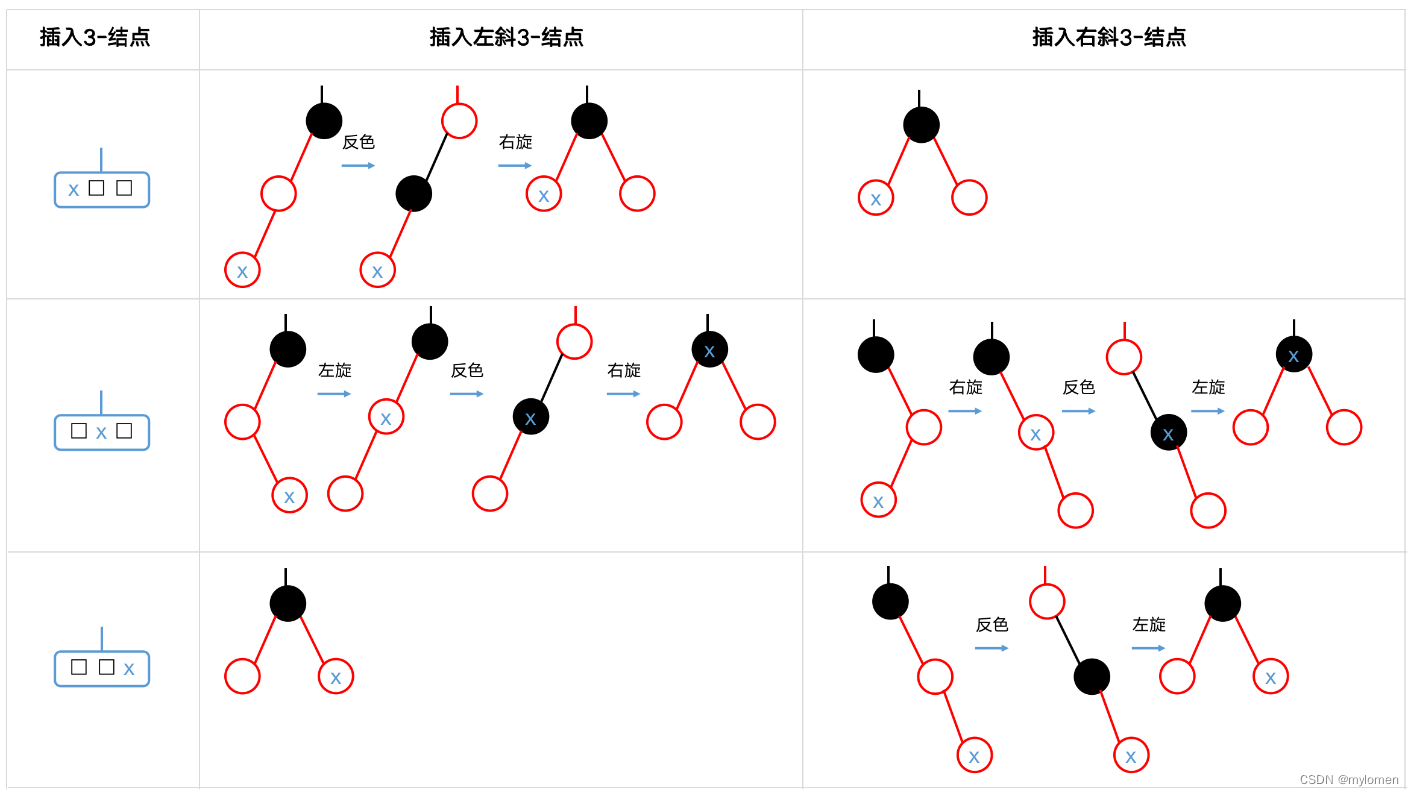
从上图中可以看出,当待插入结点在一黑色结点下插入时,直接插入而无需其他处理。
插入4-结点 (4分解为三个2-结点后其中一个2变3)
若在一红色结点下插入,且该红结点有一红色兄弟结点时,那么这个红结点就代表了4-结点 (
与它的黑父结点以及红色兄弟结点构成4-结点),也就是此时我们会将x 插入一个4-结点。
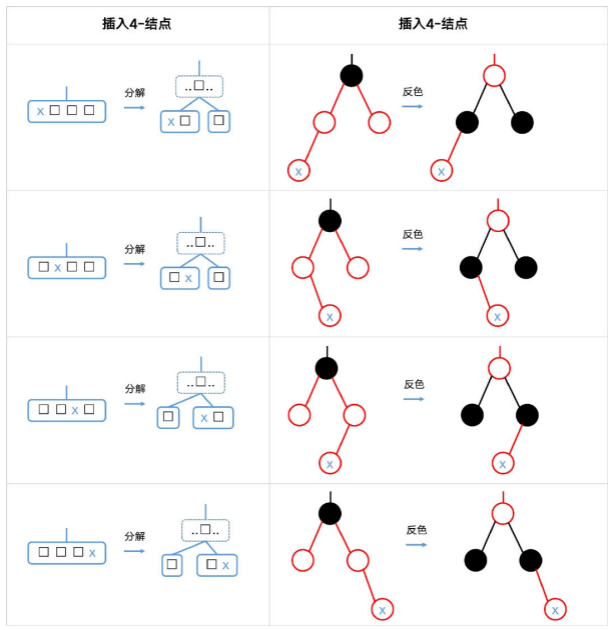
由图可以发现:插入节点的父节点是红色节点且叔叔节点也是红色,则就是插入4-节点的场景。
插入节点代码
public boolean insert(int value) {//如果根节点为空if (this.root == null) {this.root = new RbNode(value);this.root.color = false;return true;}//寻找位置RbNode myParent = this.root;while (myParent.left != null || myParent.right != null) {//新增数据 如果大于当前节点数值,则继续比较当前节点的右节点if (value > myParent.val) {if (myParent.right == null) {break;}//查看子节点myParent = myParent.right;} else if (value < myParent.val) {if (myParent.left == null) {break;}//查看子节点myParent = myParent.left;} else {return false;}}//初始化当前节点RbNode curNode = new RbNode(value);curNode.parent = myParent;if (value < myParent.val) {myParent.left = curNode;} else if (value > myParent.val) {myParent.right = curNode;} else {return false;}//修正insert_fix(curNode);//节点数量+1size++;return true;
}
插入节点修正代码
/*** 根据经典红黑树和 2-3-4 完全对应的关系,新增节点总共分为三种场景* - 2-3-4 树 插入2-结点 (2变3)* - 2-3-4 树 插入3-结点 (3变4)* - 2-3-4 树 插入4-结点 (插入4-结点 (4分解为三个2-结点后其中一个2变3))** @param curNode*/
private void insert_fix(RbNode curNode) {if (curNode == null) {return;}//父节点为空,则当前节点就是rootif (curNode.parent == null) {curNode.color = false;return;}//父节点是黑色,不需要修正. (父节点是黑色,覆盖全部 2-3-4树的2节点,部分3节点场景)if (!curNode.parent.color) {return;}//以下场景父节点颜色为红色RbNode myParent = curNode.parent;RbNode myGrandParent = curNode.parent.parent;RbNode myUncle = curNode.parent.parent.left;if (myUncle != null && myUncle.val == myParent.val) {myUncle = curNode.parent.parent.right;}//2-3-4 数 --> 4节点.(父节点和叔叔节点都是红色)if (myUncle != null && myUncle.color) {//第一步交换颜色color_flip_up(curNode.parent.parent);//1. x000。//2. 0x00。//3. 00x0。//4. 000x。//继续上溯调整insert_fix(curNode.parent.parent);return;}//2-3-4 数 --> 3节点.(叔叔节点不是红色或者不存在,父节点是红色) 假设插入节点是x,总共三种情况int min = Math.min(Math.min(curNode.val, myParent.val), myGrandParent.val);int max = Math.max(Math.max(curNode.val, myParent.val), myGrandParent.val);//1. x00。if (curNode.val == min) {//由于排除了 父节点是黑色,所以排除了 第一个0是父节点的场景,因此 只剩一种场景 第二个0是父节点.//所以先对第一和第二个0变色,再对第一个0右旋. 得到第一个0成为父节点,x成为左子节点,第二个0成为右子节点效果。color_flip_up(curNode.parent.parent);rotate_right(curNode.parent.parent);}//2. 0x0else if (curNode.val > min && curNode.val < max) {//场景1 第一个0 是祖父节点。if (curNode.parent.val < curNode.parent.parent.val) {//x左旋;x和第一个0交换颜色;x右旋rotate_left(curNode.parent);color_flip_up(curNode.parent);rotate_right(curNode.parent);}//场景2 第二个0 是祖父节点else {// x右旋;x和第一个0交换颜色;x左旋rotate_right(curNode.parent);color_flip_up(curNode.parent);rotate_left(curNode.parent);}}//3. 00xelse {//由于排除了 父节点是黑色,所以排除了 第二个0是父节点的场景,因此 只剩一种场景 第一个0是父节点.//先将第一个和第二个0 交换颜色,然后左旋第二个0color_flip_up(curNode.parent.parent);rotate_left(curNode.parent.parent);}
}
红黑二叉树删除节点
删除操作据说是最难的部分,掌握了删除逻辑约等于掌握了红黑二叉树。
2-3-4 树删除节点的场景
以key 是否在叶子结点中划分
| 2-3-4树删除 x 情形 | 删除操作 |
|---|---|
| 情形1: x 不在叶子结点中 | 用x 的后继键值替换 x,然后删除后继键值 ※ 后继键必为某叶子结点中的最小键 |
| 情形2: x 在叶子结点中 | 直接删除目标键值 ※ 若目标键在2-结点中,删除后失去2-3-4树结构性质,要调整 |
红黑树删除结点情形
| 红黑树删除结点 x 情形 | 删除操作 |
|---|---|
| 情形a: x 有左右子结点 | 用后继结点 (的键值) 替换 x (的键值),然后删除后继结点 ※ 删除后继结点必为情形b或情形c |
| 情形b: x 有一个子结点 | 建立子结点与 x.parent$ 的链接,然后删除 x ※ x 及其子结点构成3-结点,删除后不影响同构 |
| 情形c: x 无子结点 | 删除 x ※ x 对应2-3-4树中的多种情形,可能为红或黑,若为2-3-4树中的2-结点,则删除后失同构,需调整 |
删除调整
通过上述分析,我们发现仅有 x 无孩子结点且为黑 时才需要恢复同构。
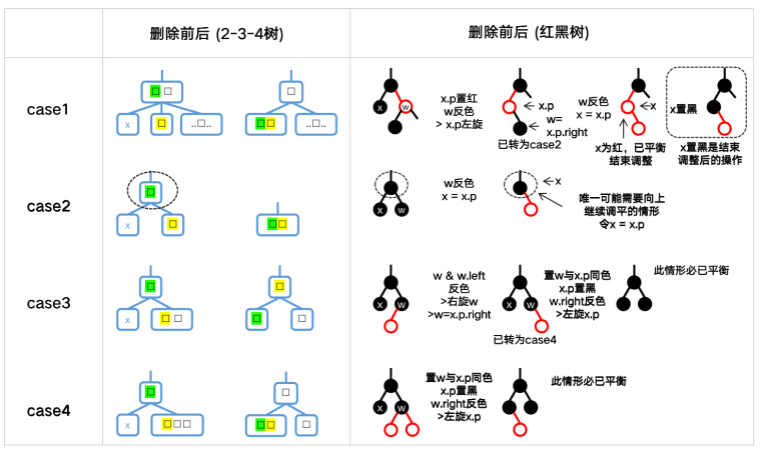
为方便叙述,我们将前述归约出的4种情形与「算法导论」给出的 case1~4 对照如下。
| 算法导论4情形 | 对应前述4情形 |
|---|---|
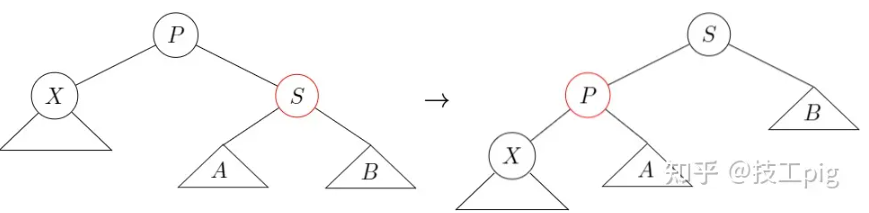
| case1: w 为红色 | 情形x-3 只需对 x.p$ 置红及 w 反色并左旋 x.p$ 后转为后续情形 |
| case2: w 为黑色,且其孩子左黑右黑 | 情形1-1 |
| case3: w 为黑色,且其孩子左红右黑 | 情形2-1左侧 只需对 w 及 w.left$ 反色并右旋 w 即为 case4 |
| case4: w 为黑色,且其孩子左黑右红或左红右红 | 情形2-1右侧 & 情形3-1 |
※ w 是待删除结点 X 的兄弟结点。
删除操作代码
public boolean remove(int value) {//find 节点RbNode curNode = find(value);if (curNode == null) {return false;}//元素数量减少1size--;//当前节点 无父节点且无孩子节点,则当前节点是跟节点且只剩唯一节点。if (curNode.parent == null && curNode.left == null && curNode.right == null) {curNode.parent = curNode.left = curNode.right = null;this.root = null;return true;}//1. 2-3-4数key 不在叶子节点中。(根据中序遍历可知: 此时当前节点一定有后继节点,且后继节点一定在叶子节点中)。if (curNode.left != null && curNode.right != null) {RbNode successorNode = findSuccessorNode(curNode);//交换数值curNode.val = successorNode.val;//指针指向调整curNode = successorNode;}//2. 2-3-4数key 在叶子节点中(直接删除目标键值然后修正2-3-4数平衡)。RbNode children = curNode.left != null ? curNode.left : curNode.right;//2-a. 红黑二叉树节点 curNode 有一个子节点(左子节点或者右子节点)。// [此种场景保证了 curNode一定是黑色,其子节点一定是红色。删除curNode后,子节点变黑即可保持红黑树性质。不需要调整]if (children != null) {//先处理父节点关系RbNode parent = curNode.parent;if (parent == null) {this.root = children;} else if (parent.left.val == curNode.val) {parent.left = children;} else {parent.right = children;}//再处理当前节点curNode.parent = curNode.left = curNode.right = null;//最后处理子节点children.parent = parent;children.color = false;}//2-b. 红黑二叉树节点 curNode 没有子节点。 此种场景最复杂,当curNode 是红色需要修正。else {//待删除的节点是黑色 则需要修复if (!curNode.color) {remove_fix(curNode);}RbNode parent = curNode.parent;if (parent != null) {//先处理父节点if (parent.left != null && curNode.val == parent.left.val) {curNode.parent.left = null;} else {curNode.parent.right = null;}//再处理当前节点curNode.parent = null;}}return true;
}
删除修复代码
void remove_fix(RbNode curNode) {//2-3-4 树 3-节点和 4-节点 或者根节点 直接删除即可。 不需要修补逻辑//当前节点是红色 则停止修正。(删除修复操作在遇到被删除的节点是红色节点或者到达root节点时,修复操作完毕。)//需要做的处理是从兄弟节点上借调黑色的节点过来,如果兄弟节点没有黑节点可以借调的话,就只能往上追溯,将每一级的黑节点数减去一个,使得整棵树符合红黑树的定义。//删除操作的总体思想是从兄弟节点借调黑色节点使树保持局部的平衡,如果局部的平衡达到了,就看整体的树是否是平衡的,如果不平衡就接着向上追溯调整。//算法导论4情形。 vs 2-3-4 四种情形.(w 是待删除节点的兄弟节点)//删除修复操作分为四种情况(删除黑节点后)://case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]//case 2: w是黑色,且其孩子左黑右黑//case 3: w是黑色,且其孩子左红右黑。(只需对 w 和 w.left 变色,然后右旋w,即为场景4)//case 4: w是黑色,且其孩子左黑右红或者左红右红while (curNode.val != this.root.val && colorBlack(curNode)) {//待删除节点是左节点(一切为了 右边兄弟左旋).if (curNode.parent.left != null && curNode.val == curNode.parent.left.val) {RbNode w = curNode.parent.right;//case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]if (w.color) {//1.w置黑w.color = false;//2. 待删除节点父节点置红curNode.parent.color = true;//3.待删除节点父节点左旋rotate_left(curNode.parent);//更新兄弟节点位置w = curNode.parent.right;}//case 2:w是黑色,且其孩子左黑右黑(w变换颜色,然后向上调整).if (colorBlack(w.left) && colorBlack(w.right)) {//此时 w 一定是黑色(反色目的是让它作为一个3-结点中的红色结点)。w.color = true;//继续向上调整[唯一一个向上调整]curNode = curNode.parent;//如果当前节点是红色 则已经平衡if (curNode.color) {break;}} else {//case 3: w是黑色,且其孩子左红右黑。(只需对 w 和 w.left 变色,然后右旋w,即为场景4)if (colorBlack(w.right)) {//w.left 置黑w.left.color = false;//w 置红w.color = true;//右旋wrotate_right(w);//调整兄弟节点w = curNode.parent.right;}//case 4: w是黑色,且其孩子左黑右红或者左红右红.//置w和curNode.parent 相同颜色w.color = curNode.parent.color;//置curNode.parent 黑色curNode.parent.color = false;//置w.right 黑色w.right.color = false;//左旋curNode.parentrotate_left(curNode.parent);//兄弟节点不存在或者兄弟节点的子节点不存在 则表示已经平衡. 另:case3和case4调整后必平衡。curNode=this.rootw = curNode.parent.right;if (w == null || (w.left == null && w.right == null)) {break;}}} else {//待删除节点是右节点RbNode w = curNode.parent.left;//case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]if (w.color) {//curNode.parent 置黑curNode.parent.color = true;//w置黑w.color = false;//curNode.parent右旋rotate_right(curNode.parent);//更新兄弟节点位置w = curNode.parent.left;}//case 2:w是黑色,且其孩子左黑右黑(w变换颜色,然后向上调整).if (colorBlack(w.left) && colorBlack(w.right)) {//此时 w 一定是黑色(反色目的是让它作为一个3-结点中的红色结点)。w.color = true;//继续向上调整[唯一一个向上调整]curNode = curNode.parent;//如果当前节点是红色 则已经平衡if (curNode.color) {break;}} else {//case 3: w是黑色,且其孩子右红左黑。(只需对 w 和 w.right 变色,然后右旋w,即为场景4)if (colorBlack(w.left)) {//w.right 置黑w.right.color = false;//w 置红w.color = true;//左旋wrotate_left(w);//调整兄弟节点w = curNode.parent.left;}//case 4: w是黑色,且其孩子左红右黑或者左红右红.//置w和curNode.parent 相同颜色w.color = curNode.parent.color;//置curNode.parent 黑色curNode.parent.color = false;//置w.left 黑色w.left.color = false;//右旋curNode.parentrotate_right(curNode.parent);//兄弟节点不存在或者兄弟节点的子节点不存在 则表示已经平衡. 另:case3和case4调整后必平衡。curNode=this.rootw = curNode.parent.left;if (w == null || (w.left == null && w.right == null)) {break;}}}}// while结束要么是case3/case4调整后已平衡 x被被置为root后主动退出,// 要么是case1/case2 x为红。若为前者无需此句(此时的root一定是黑的)// 若为后者,说明此时的x结点是原3-结点或4-结点出借的结点,如果还保持红色,// 将无法脱离原3-结点或4-结点 (2-3-4树),因此必须置黑。// 此句也可以写成这样: if(x != root) x.color = BLACK//curNode.color = false;
}完整代码demo
import java.util.LinkedList;
import java.util.Queue;/*** 对应2-3-4 树;* 规则、设定:* 新插入的节点是红色的;* 新插入节点的父节点是红色才需要修复;* 不支持插入相同的数字,如果插入数字相同直接返回。* 在线验证调试: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html*/
public class RBTree {static class RbNode {/*** 父级*/RbNode parent;/*** true:红色;false 黑色[默认]*/boolean color;/*** 节点数值,简单起见也当作key使用*/int val;/*** 左节点*/RbNode left;/*** 右节点*/RbNode right;public RbNode(int val) {this.val = val;//新插入的节点是红色的this.color = true;}}/*** 主节点*/RbNode root;/*** 尺寸*/int size;public boolean insert(int value) {//如果根节点为空if (this.root == null) {this.root = new RbNode(value);this.root.color = false;return true;}//寻找位置RbNode myParent = this.root;while (myParent.left != null || myParent.right != null) {//新增数据 如果大于当前节点数值,则继续比较当前节点的右节点if (value > myParent.val) {if (myParent.right == null) {break;}//查看子节点myParent = myParent.right;} else if (value < myParent.val) {if (myParent.left == null) {break;}//查看子节点myParent = myParent.left;} else {return false;}}//初始化当前节点RbNode curNode = new RbNode(value);curNode.parent = myParent;if (value < myParent.val) {myParent.left = curNode;} else if (value > myParent.val) {myParent.right = curNode;} else {return false;}//修正insert_fix(curNode);//节点数量+1size++;return true;}/*** 根据经典红黑树和 2-3-4 完全对应的关系,新增节点总共分为三种场景* - 2-3-4 树 插入2-结点 (2变3)* - 2-3-4 树 插入3-结点 (3变4)* - 2-3-4 树 插入4-结点 (插入4-结点 (4分解为三个2-结点后其中一个2变3))** @param curNode*/private void insert_fix(RbNode curNode) {if (curNode == null) {return;}//父节点为空,则当前节点就是rootif (curNode.parent == null) {curNode.color = false;return;}//父节点是黑色,不需要修正. (父节点是黑色,覆盖全部 2-3-4树的2节点,部分3节点场景)if (!curNode.parent.color) {return;}//以下场景父节点颜色为红色RbNode myParent = curNode.parent;RbNode myGrandParent = curNode.parent.parent;RbNode myUncle = curNode.parent.parent.left;if (myUncle != null && myUncle.val == myParent.val) {myUncle = curNode.parent.parent.right;}//2-3-4 数 --> 4节点.(父节点和叔叔节点都是红色)if (myUncle != null && myUncle.color) {//第一步交换颜色color_flip_up(curNode.parent.parent);//1. x000。//2. 0x00。//3. 00x0。//4. 000x。//继续上溯调整insert_fix(curNode.parent.parent);return;}//2-3-4 数 --> 3节点.(叔叔节点不是红色或者不存在,父节点是红色) 假设插入节点是x,总共三种情况int min = Math.min(Math.min(curNode.val, myParent.val), myGrandParent.val);int max = Math.max(Math.max(curNode.val, myParent.val), myGrandParent.val);//1. x00。if (curNode.val == min) {//由于排除了 父节点是黑色,所以排除了 第一个0是父节点的场景,因此 只剩一种场景 第二个0是父节点.//所以先对第一和第二个0变色,再对第一个0右旋. 得到第一个0成为父节点,x成为左子节点,第二个0成为右子节点效果。color_flip_up(curNode.parent.parent);rotate_right(curNode.parent.parent);}//2. 0x0else if (curNode.val > min && curNode.val < max) {//场景1 第一个0 是祖父节点。if (curNode.parent.val < curNode.parent.parent.val) {//x左旋;x和第一个0交换颜色;x右旋rotate_left(curNode.parent);color_flip_up(curNode.parent);rotate_right(curNode.parent);}//场景2 第二个0 是祖父节点else {// x右旋;x和第一个0交换颜色;x左旋rotate_right(curNode.parent);color_flip_up(curNode.parent);rotate_left(curNode.parent);}}//3. 00xelse {//由于排除了 父节点是黑色,所以排除了 第二个0是父节点的场景,因此 只剩一种场景 第一个0是父节点.//先将第一个和第二个0 交换颜色,然后左旋第二个0color_flip_up(curNode.parent.parent);rotate_left(curNode.parent.parent);}}/*** 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。* 左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。** @param p*/void rotate_left(RbNode p) {// 1.处理当前节点的父节点if (p.parent == null) {this.root = p.right;//1} else if (p.parent.left != null && p.parent.left.val == p.val) {p.parent.left = p.right;//1} else {p.parent.right = p.right;//1}// 2.处理历史右子节点。(当前父节点)p.right.parent = p.parent;//2RbNode rightLeftNode = p.right.left;p.right.left = p;//3// 3. 处理当前节点p.parent = p.right;//4p.right = rightLeftNode;//5// 4.处理历史右节点的左子节点if (rightLeftNode != null) {rightLeftNode.parent = p;//6}}/*** 右旋: 以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。* 右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。** @param p*/void rotate_right(RbNode p) {// 1.处理当前节点的父节点if (p.parent == null) {this.root = p.left;//1} else if (p.parent.left != null && p.parent.left.val == p.val) {p.parent.left = p.left;//1} else {p.parent.right = p.left;//1}// 2.处理历史左子节点。(当前父节点)p.left.parent = p.parent;//2RbNode leftRightNode = p.left.right;p.left.right = p;//3// 3. 处理当前节点p.parent = p.left;//4p.left = leftRightNode;//5// 4.处理历史左节点的右子节点if (leftRightNode != null) {leftRightNode.parent = p;//6}}/*** @param node*/void color_flip_up(RbNode node) {node.color = true;//子节点变黑if (node.left != null) {node.left.color = false;}if (node.right != null) {node.right.color = false;}}/*** 是否是黑色。* 注:空节点当作黑色** @param node* @return*/boolean colorBlack(RbNode node) {return node == null || !node.color;}/*** 2-3-4 树 删除key 按照key 是否在叶子节点中划分为两种场景:* 1. key 不在叶子节点中-->用key 后继键值替换key,然后删除后继键值(后继键必为某叶子结点中的最小键)。* 2. key 在叶子节点中-->直接删除目标键值(若目标键在2-结点中,删除后失去2-3-4树结构性质,要调整)。* <p>* 红黑树删除节点key 情形以删除节点的子节点情况划分3种场景* 1. key 有左右子节点-->用候机节点替换key(数值和节点关系),然后删除后继节点(删除后继节点必为情形2或者情形3?不是 1/2/3?)。* 2. key 有一个子节点-->简历子节点与 key节点的父节点的链接,然后删除key节点(key极其子节点构成3-节点,删除后不影响同构)。* 3. key 没有子节点-->直接删除key(key如果对应2-3-4树中的2-节点,则删除后失去同构,需修正。)。* <p>* ⚠️:依据BST数删除节点的规则(交换当前节点和后继绩点,然后删除后继节点)。无论删除的结点在何处,最终都会 删除一个对应于2-3-4树上的叶子结点。** @param value* @return*/public boolean remove(int value) {//find 节点RbNode curNode = find(value);if (curNode == null) {return false;}//元素数量减少1size--;//当前节点 无父节点且无孩子节点,则当前节点是跟节点且只剩唯一节点。if (curNode.parent == null && curNode.left == null && curNode.right == null) {curNode.parent = curNode.left = curNode.right = null;this.root = null;return true;}//1. 2-3-4数key 不在叶子节点中。(根据中序遍历可知: 此时当前节点一定有后继节点,且后继节点一定在叶子节点中)。if (curNode.left != null && curNode.right != null) {RbNode successorNode = findSuccessorNode(curNode);//交换数值curNode.val = successorNode.val;//指针指向调整curNode = successorNode;}//2. 2-3-4数key 在叶子节点中(直接删除目标键值然后修正2-3-4数平衡)。RbNode children = curNode.left != null ? curNode.left : curNode.right;//2-a. 红黑二叉树节点 curNode 有一个子节点(左子节点或者右子节点)。// [此种场景保证了 curNode一定是黑色,其子节点一定是红色。删除curNode后,子节点变黑即可保持红黑树性质。不需要调整]if (children != null) {//先处理父节点关系RbNode parent = curNode.parent;if (parent == null) {this.root = children;} else if (parent.left.val == curNode.val) {parent.left = children;} else {parent.right = children;}//再处理当前节点curNode.parent = curNode.left = curNode.right = null;//最后处理子节点children.parent = parent;children.color = false;}//2-b. 红黑二叉树节点 curNode 没有子节点。 此种场景最复杂,当curNode 是红色需要修正。else {//待删除的节点是黑色 则需要修复if (!curNode.color) {remove_fix(curNode);}RbNode parent = curNode.parent;if (parent != null) {//先处理父节点if (parent.left != null && curNode.val == parent.left.val) {curNode.parent.left = null;} else {curNode.parent.right = null;}//再处理当前节点curNode.parent = null;}}return true;}/*** 中序遍历,查找当前节点的后续节点(寻找继承人)** @param curNode* @return*/RbNode findSuccessorNode(RbNode curNode) {if (curNode == null) {return null;}//1. 向下搜索-> 当前节点有 右子节点if (curNode.right != null) {RbNode mySuccessorNode = curNode;while (mySuccessorNode.left != null) {mySuccessorNode = mySuccessorNode.left;}return mySuccessorNode;}//2. 向上搜索-> 当前节点没有 右子节点.RbNode parent = curNode.parent;//如果没有父节点,则当前节点是root节点,直接返回nullif (parent == null) {return null;}//如果当前节点是父节点的左子节点,则当前节点的后继节点就是 父节点if (parent.left == curNode) {return parent;}//向上搜索当前节点的父节点...中的第一个左节点while (parent.parent != null && parent.parent.right == parent) {parent = parent.parent;}return parent.parent;}/*** 删除修复。【只有当前节点是黑色才会修复】** @param curNode*/void remove_fix(RbNode curNode) {//2-3-4 树 3-节点和 4-节点 或者根节点 直接删除即可。 不需要修补逻辑//当前节点是红色 则停止修正。(删除修复操作在遇到被删除的节点是红色节点或者到达root节点时,修复操作完毕。)//需要做的处理是从兄弟节点上借调黑色的节点过来,如果兄弟节点没有黑节点可以借调的话,就只能往上追溯,将每一级的黑节点数减去一个,使得整棵树符合红黑树的定义。//删除操作的总体思想是从兄弟节点借调黑色节点使树保持局部的平衡,如果局部的平衡达到了,就看整体的树是否是平衡的,如果不平衡就接着向上追溯调整。//算法导论4情形。 vs 2-3-4 四种情形.(w 是待删除节点的兄弟节点)//删除修复操作分为四种情况(删除黑节点后)://case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]//case 2: w是黑色,且其孩子左黑右黑//case 3: w是黑色,且其孩子左红右黑。(只需对 w 和 w.left 变色,然后右旋w,即为场景4)//case 4: w是黑色,且其孩子左黑右红或者左红右红while (curNode.val != this.root.val && colorBlack(curNode)) {//待删除节点是左节点(一切为了 右边兄弟左旋).if (curNode.parent.left != null && curNode.val == curNode.parent.left.val) {RbNode w = curNode.parent.right;//case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]if (w.color) {//1.w置黑w.color = false;//2. 待删除节点父节点置红curNode.parent.color = true;//3.待删除节点父节点左旋rotate_left(curNode.parent);//更新兄弟节点位置w = curNode.parent.right;}//case 2:w是黑色,且其孩子左黑右黑(w变换颜色,然后向上调整).if (colorBlack(w.left) && colorBlack(w.right)) {//此时 w 一定是黑色(反色目的是让它作为一个3-结点中的红色结点)。w.color = true;//继续向上调整[唯一一个向上调整]curNode = curNode.parent;//如果当前节点是红色 则已经平衡if (curNode.color) {break;}} else {//case 3: w是黑色,且其孩子左红右黑。(只需对 w 和 w.left 变色,然后右旋w,即为场景4)if (colorBlack(w.right)) {//w.left 置黑w.left.color = false;//w 置红w.color = true;//右旋wrotate_right(w);//调整兄弟节点w = curNode.parent.right;}//case 4: w是黑色,且其孩子左黑右红或者左红右红.//置w和curNode.parent 相同颜色w.color = curNode.parent.color;//置curNode.parent 黑色curNode.parent.color = false;//置w.right 黑色w.right.color = false;//左旋curNode.parentrotate_left(curNode.parent);//兄弟节点不存在或者兄弟节点的子节点不存在 则表示已经平衡. 另:case3和case4调整后必平衡。curNode=this.rootw = curNode.parent.right;if (w == null || (w.left == null && w.right == null)) {break;}}} else {//待删除节点是右节点RbNode w = curNode.parent.left;//case 1: w是红色。[只需对当前节点父节点置红以及w节点变黑并且左旋当前节点的父节点,即可转换成下述 2-4场景]if (w.color) {//curNode.parent 置黑curNode.parent.color = true;//w置黑w.color = false;//curNode.parent右旋rotate_right(curNode.parent);//更新兄弟节点位置w = curNode.parent.left;}//case 2:w是黑色,且其孩子左黑右黑(w变换颜色,然后向上调整).if (colorBlack(w.left) && colorBlack(w.right)) {//此时 w 一定是黑色(反色目的是让它作为一个3-结点中的红色结点)。w.color = true;//继续向上调整[唯一一个向上调整]curNode = curNode.parent;//如果当前节点是红色 则已经平衡if (curNode.color) {break;}} else {//case 3: w是黑色,且其孩子右红左黑。(只需对 w 和 w.right 变色,然后右旋w,即为场景4)if (colorBlack(w.left)) {//w.right 置黑w.right.color = false;//w 置红w.color = true;//左旋wrotate_left(w);//调整兄弟节点w = curNode.parent.left;}//case 4: w是黑色,且其孩子左红右黑或者左红右红.//置w和curNode.parent 相同颜色w.color = curNode.parent.color;//置curNode.parent 黑色curNode.parent.color = false;//置w.left 黑色w.left.color = false;//右旋curNode.parentrotate_right(curNode.parent);//兄弟节点不存在或者兄弟节点的子节点不存在 则表示已经平衡. 另:case3和case4调整后必平衡。curNode=this.rootw = curNode.parent.left;if (w == null || (w.left == null && w.right == null)) {break;}}}}// while结束要么是case3/case4调整后已平衡 x被被置为root后主动退出,// 要么是case1/case2 x为红。若为前者无需此句(此时的root一定是黑的)// 若为后者,说明此时的x结点是原3-结点或4-结点出借的结点,如果还保持红色,// 将无法脱离原3-结点或4-结点 (2-3-4树),因此必须置黑。// 此句也可以写成这样: if(x != root) x.color = BLACK//curNode.color = false;}public RbNode find(int value) {RbNode myParent = this.root;while (myParent != null) {if (value > myParent.val) {if (myParent.right == null) {return null;}myParent = myParent.right;} else if (value < myParent.val) {if (myParent.left == null) {return null;}myParent = myParent.left;} else {return myParent;}}return null;}/*** 广度优先遍历*/public void printTree() {Queue<RbNode> queue = new LinkedList<>();if (this.root == null) {return;}//首次queue.add(this.root);//开始遍历while (!queue.isEmpty()) {//遍历int length = queue.size();for (int i = 0; i < length; i++) {//从队尾取出数据RbNode n = queue.poll();System.out.print((n.color ? "R" : "B") + ":" + n.val + "\t");//从队首增加if (n.left != null) {queue.add(n.left);}if (n.right != null) {queue.add(n.right);}}System.out.println();}}public static void main(String[] args) {RBTree rbTree = new RBTree();System.out.println(rbTree.insert(1));System.out.println(rbTree.insert(2));System.out.println(rbTree.insert(3));System.out.println(rbTree.insert(4));System.out.println(rbTree.insert(5));
// rbTree.printTree();System.out.println(rbTree.insert(6));
// rbTree.printTree();System.out.println(rbTree.insert(7));
// rbTree.printTree();System.out.println(rbTree.insert(8));
// rbTree.printTree();System.out.println(rbTree.insert(9));
// rbTree.printTree();System.out.println(rbTree.insert(10));
// rbTree.printTree();System.out.println("###### 开始删除操作 ######");for (int i = 10; i >= 1; i--) {if (i == 1) {System.out.println(i);}System.out.println(rbTree.remove(i));rbTree.printTree();}}
}参考(如有冒犯请联系删除)
文中部分定义和图片参考链接
相关文章:

从2-3-4树开始理解红黑二叉树(JAVA代码手撸版)
经典的红黑二叉树在新增/删除数据时维持自平衡始终对应着一个2-3-4 树。本文只关注2-3-4 对应的经典红黑二叉树。 暂时不考虑 2-3 树对应的左倾红黑二叉树。 背景知识 2-3-4 树简介 一棵 2-3-4 树的结点分为 内部结点 (internal nodes) 和 叶子结点 (leaf nodes) ,…...

模板类与继承
1模板类继承普通类(常见) #include<iostream> using namespace std; class AA { public:int m_a;AA(int a) :m_a(a) { cout << "调用了AA的构造函数\n"; }void func1() { cout << "调用func1()…...

随手记:uniapp图片展示,剩余的堆叠
UI效果图: 实现思路: 循环图片数组,只展示几张宽度就为几张图片边距的宽度,剩下的图片直接堆叠展示 点击预览的时候传入当前的下标,如果是点击堆叠的话,下标从堆叠数量开始计算 <template><…...

微服务迁移、重构最佳经验
1. 了解现有的单体应用: - 应用架构和技术栈 要了解现有的应用架构和技术栈,可以采取以下几个步骤: 1. 了解应用的背景和目标:首先要了解应用的背景和目标,包括应用所属的行业、应用的类型(例如Web应用、移动应用等…...

【Python】从0开始的Django基础
Django框架基础 unit01一、Django基础1.1 什么是Django?1.2 安装与卸载1.2.1 Python与Django的版本1.2.2 安装1.2.3 查看Django版本1.2.4 卸载 二、Django项目2.1 概述2.2 创建项目2.3 启动项目2.4 项目的目录结构2.5 配置 三、URL 调度器3.2 定义URL路由3.2 定义首页的路由3.…...
红黑树(数据结构篇)
数据结构之红黑树 红黑树(RB-tree) 概念: 红黑树是AVL树的变种,它是每一个节点或者着成红色,或者着成黑色的一棵二叉查找树。对红黑树的操作在最坏情形下花费O(logN)时间,它的插入操作使用的是非递归形式实现红黑树的高度最多是…...
)
高级视频编码器性能对比(H265、VP9、AV1)
1、背景介绍 目前在视频编解码器中,H264已经成为绝对的主流,被大部分设备、浏览器所支持。虽然有更先进的编码器推出,但是受限于推广速度和设备支持成本,一直未能成为主流。 今年公司目标是持续降本增效,现在将”屠刀…...
示例:WPF中DataGrid简单设置合并列头
一、目的:应用DataGridTemplateColumn列模板,去拆分列头和单元格布局的方式设置列头合并样式 二、实现 效果如下 三、环境 VS2022 四、示例 应用DataGridTemplateColumn自定义列头信息和单元格信息 <DataGrid AutoGenerateColumns"False"…...
Matlab图像处理——细胞图像的分割和计数显示
一. 项目介绍 使用MATLAB编写的细胞图像分割及计数系统,实现了对图像内细胞的计数,以及对每个细胞周长和面积的测量,并分别展示了分割后的每个细胞的图像。实验步骤共分为图像预处理、图像预分割、空洞填充、黏连细胞分割、细胞个数统计、细胞…...

六爻排盘神机
选修课留了3000字的论文......确实,削微有那么一点小困难…… 但是,倘若我拿出已经占了6419个字符的 “六爻排盘神机” ,阁下…应该…不会…骂我吧 且看,六爻排盘神机! import random import datetime from lunarcale…...

【ARMv8/v9 GIC 系列 2.1 -- GIC SPI 中断的 pending 和 clear pending 配置】
文章目录 GIC Pending 和 Clear PendingGICD_ISPENDR<n>GICD_ICPENDR<n>参数<n>编号解释使用举例设置中断ID 100为挂起状态清除中断ID 100的挂起状态 代码实现小结 GIC Pending 和 Clear Pending 在ARMv8体系结构中,GICD_ISPENDR<n> 和 GI…...
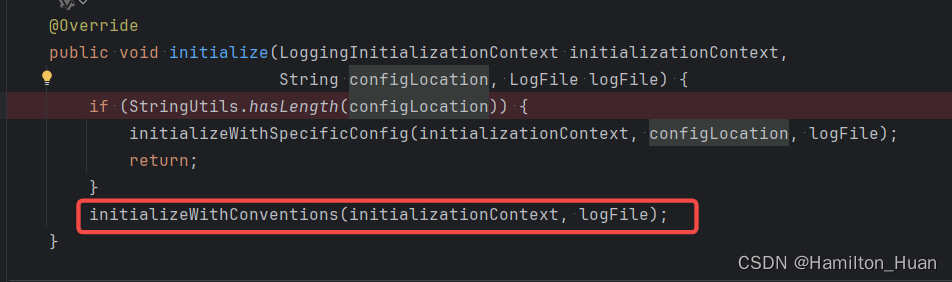
SpringBoot集成logback初始化源码解析(部分)
一.SpringBoot配置扩展点 SpringBoot日志模块使用监听的方式进行初始化,在SpringBoot项目启动后,会通知日志监听器 在日志监听器中ApplicationStartingEvent事件用来确定到底使用哪个日志系统,logback log4j等 在日志监听器中ApplicationEn…...
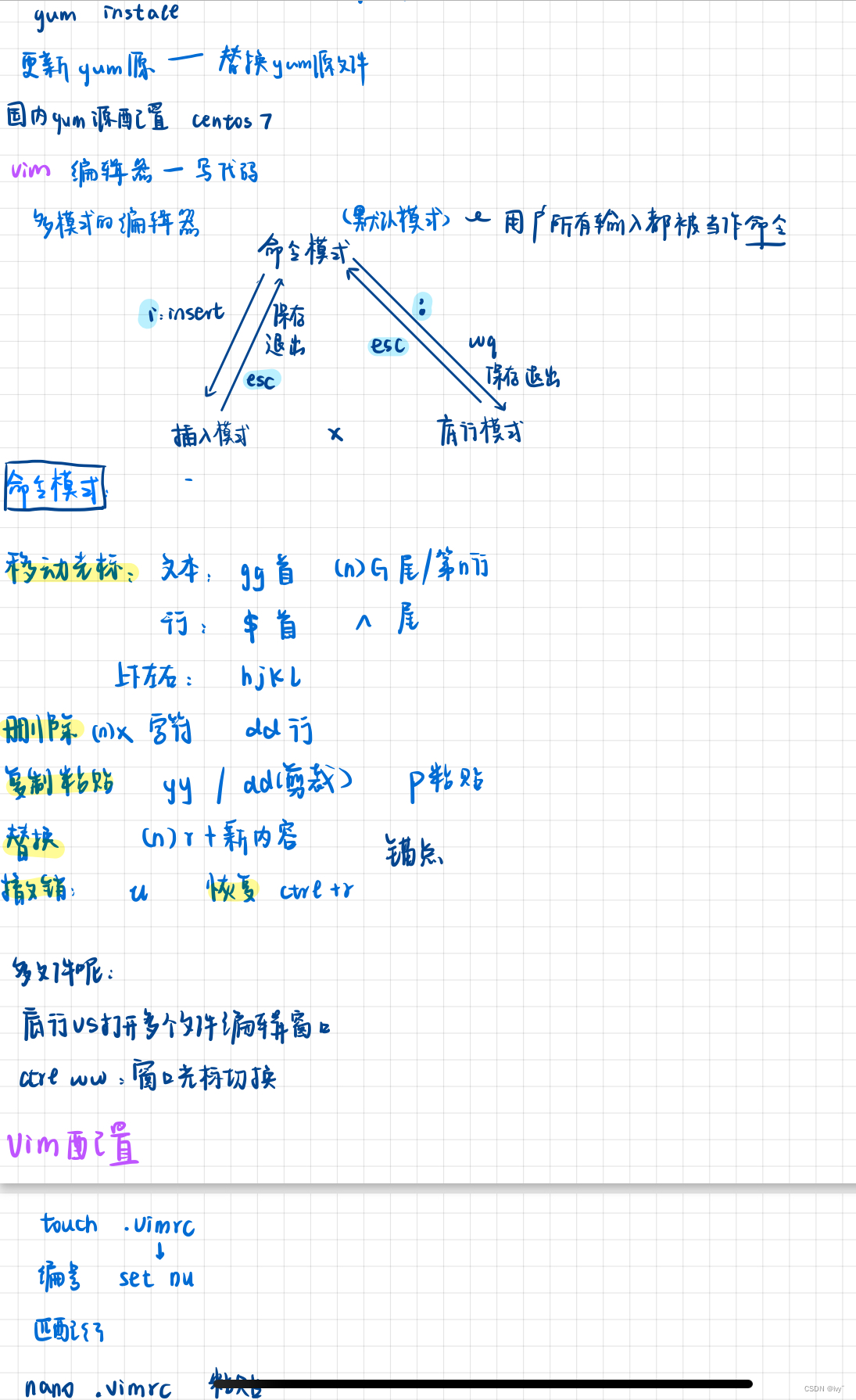
【Linux工具】yum软件包管理器与Vim编辑器的高效运用
目录 Linux 软件包管理器 YUM 什么是软件包 安装工具 rzsz 及注意事项 查看软件包 安装和卸载软件 安装软件 卸载软件 Linux 开发工具 编辑器 - Vim 使用 编辑 Vim 与 Vi 的区别 Vim 的基本概念 三种模式 Vim 的基本操作 操作尝试: Vim 命令集解释…...

Matlab数学建模实战应用:案例4 - 图像处理
目录 前言 一、图像处理基础 二、Matlab图像处理工具箱 三、案例:图像锐化、去噪和分割 步骤 1:读取和显示图像 步骤 2:图像锐化 步骤 3:图像去噪 步骤 4:图像分割 完整代码示例 四、实际应用 实例总结 总…...
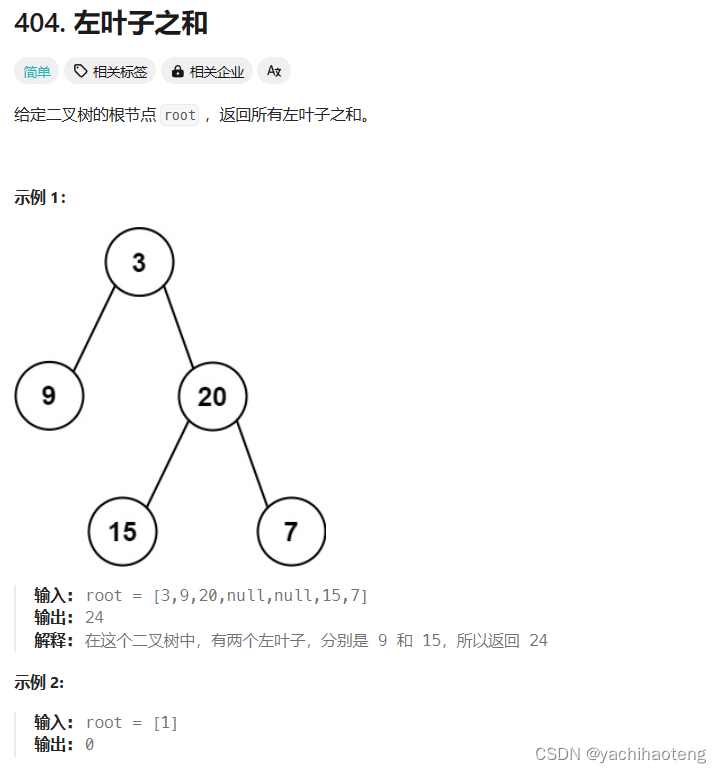
Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C 目录 257.完全二叉树的节点个数 110.平衡二叉树 257.二叉树的所有路径 404.左叶子之和 总结 257.完全二叉树的节点个数 文档讲解:代码随想录完全二叉树的节点个数 视频讲解…...

Python 基础:异常
目录 一、异常概念二、处理异常2.1 抛出异常2.2 使用 try-except 代码块2.3 使用 try-except-else 代码块2.4 静默失败 三、总结 遇到看不明白的地方,欢迎在评论中留言呐,一起讨论,一起进步! 本文参考:《Python编程&a…...

XML 应用程序
XML 应用程序 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。它是一种自我描述的语言,允许用户定义自己的标签和文档结构。XML广泛应用于各种应用程序中,包括网站开发、数据交换、文档管理等。本文将探讨XML的一些主要…...

SprringCloud Gateway动态添加路由不重启
文章目录 前言:一、动态路由必要性二、SpringCloud Gateway路由加载过程RouteDefinitionLocator接口PropertiesRouteDefinitionLocator类DiscoveryClientRouteDefinitionLocatorInMemoryRouteDefinitionRepositoryCompositeRouteDefinitionLocator类CachingRouteDef…...
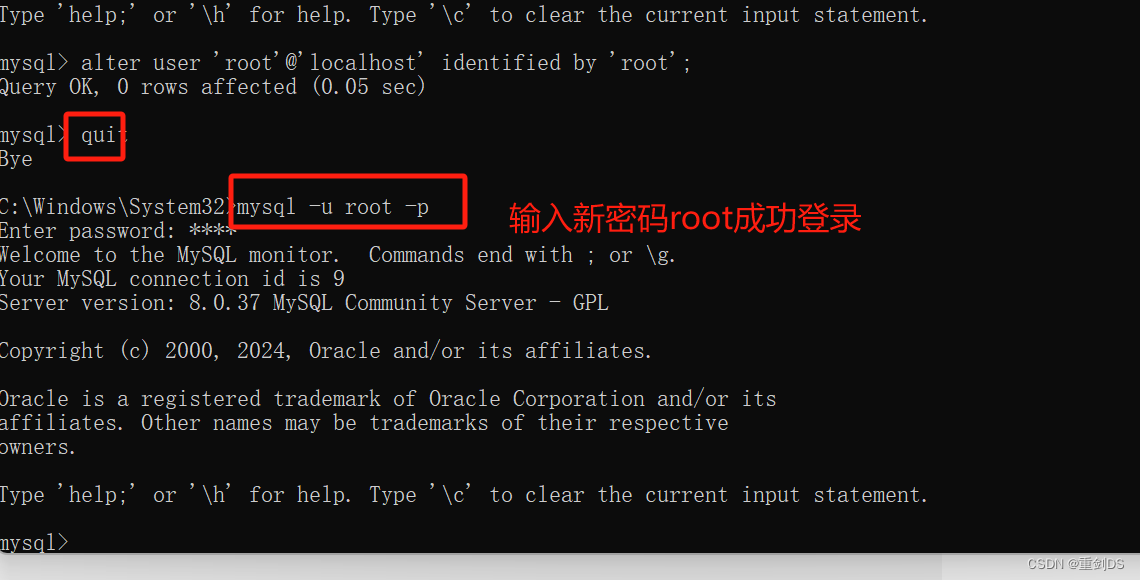
Windows安装mysql
首先去官网下载社区版本的mysql(如果连不上,挂梯子) https://www.mysql.com/downloads/ 2. 去配置环境变量path 3. 在cmd里面初始化数据库(在搜索框输入cmd,或者在资源管理器下搜索烂输入cmd回车就行) my…...
chatgpt: linux 下用纯c 编写ui
在Linux下用纯C语言编写用户界面(UI),通常会使用GTK或Xlib。GTK是一个更高级的库,提供了丰富的控件和功能,而Xlib则是一个更底层的库,提供了直接操作X Window系统的功能。 下面是一个使用GTK在Linux上创建…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
